第五章 抛体运动 章末复习(课件)-2021-2022学年【扬帆起航系列】人教版(2019)高中物理课件必修第二册(共31张PPT)
文档属性
| 名称 | 第五章 抛体运动 章末复习(课件)-2021-2022学年【扬帆起航系列】人教版(2019)高中物理课件必修第二册(共31张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-12-06 00:00:00 | ||
图片预览






文档简介
(共31张PPT)
人教版(2019)高中物理必修第二册
第五章 抛体运动
章 末 复 习
授课人:扬帆起航
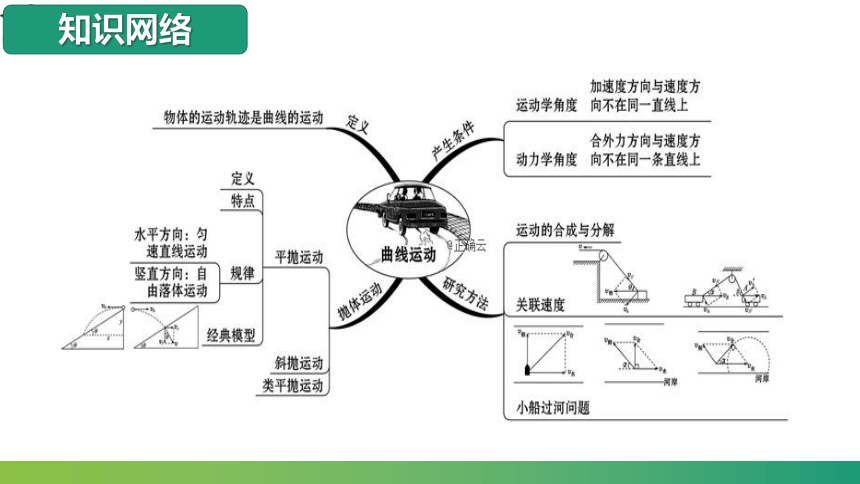
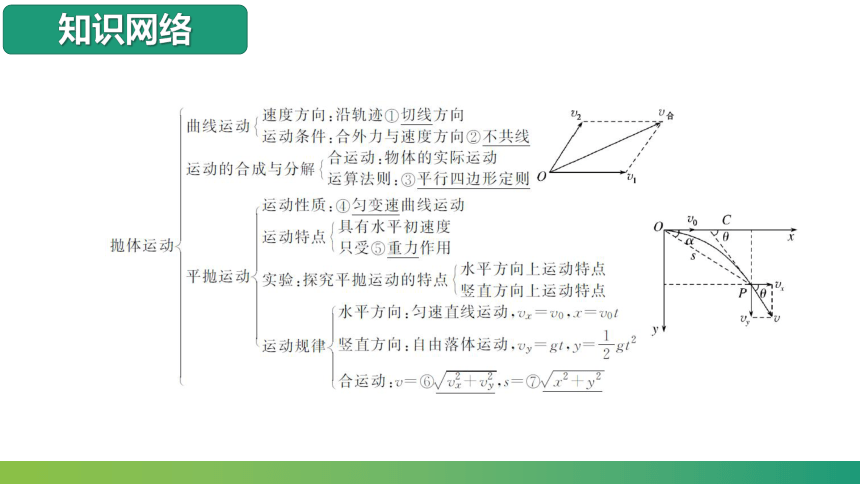
知识网络
知识网络
知识网络
课堂练习
判一判
(1)做曲线运动的物体速度大小一定发生变化.( )
(2)做曲线运动的物体加速度一定是变化的.( )
(3)曲线运动一定是变速运动.( )
(4)两个分运动的时间一定与它们合运动的时间等( )
(5)合运动的速度一定大于分运动的速度.( )
(6)两个直线运动的合运动一定是直线运动.( )
(1)×(2)×(3)√(4)√(5)×(6)×
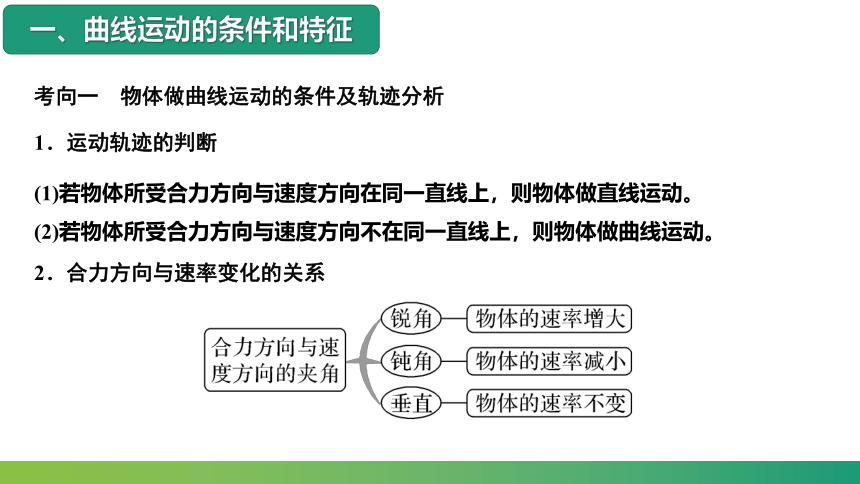
考向一 物体做曲线运动的条件及轨迹分析
1.运动轨迹的判断
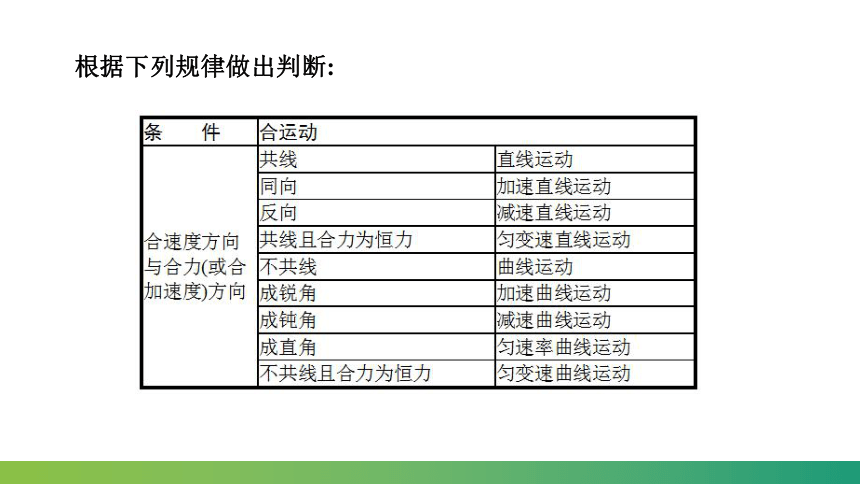
(1)若物体所受合力方向与速度方向在同一直线上,则物体做直线运动。
(2)若物体所受合力方向与速度方向不在同一直线上,则物体做曲线运动。
2.合力方向与速率变化的关系
一、曲线运动的条件和特征
3.两个直线运动的合运动性质的判断
标准:看合初速度方向与合加速度方向是否共线.
两个互成角度的分运动 合运动的性质
两个匀速直线运动 匀速直线运动
一个匀速直线运动、一个匀变速直线运动 运动
两个初速度为零的匀加速直线运动 运动
两个初速度不为零的匀变速直线运动 如果v合与a合共线,为_______
运动
如果v合与a合不共线,为_____
运动
匀变速曲线
匀加速直线
匀变速
直线
匀变
速曲线
根据下列规律做出判断:
例1 下列说法正确的是
A.做曲线运动的物体的速度一定变化
B.速度变化的运动一定是曲线运动
C.加速度恒定的运动不可能是曲线运动
D.加速度变化的运动一定是曲线运动
√
解析 做曲线运动的物体,速度方向一定改变,选项A正确;速度大小改变而方向不变的运动是直线运动,选项B错误;平抛运动是加速度恒定的曲线运动,选项C错误;加速度大小改变,但加速度方向与速度方向始终相同,这种运动是直线运动,选项D错误.
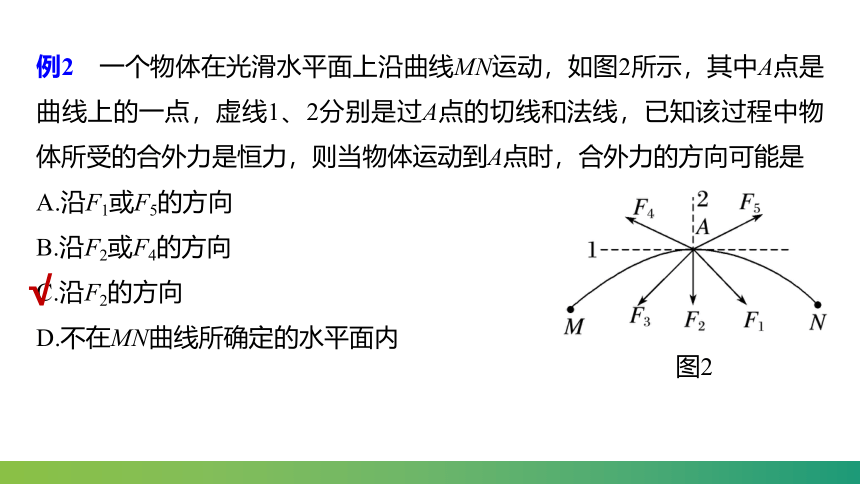
例2 一个物体在光滑水平面上沿曲线MN运动,如图2所示,其中A点是曲线上的一点,虚线1、2分别是过A点的切线和法线,已知该过程中物体所受的合外力是恒力,则当物体运动到A点时,合外力的方向可能是
A.沿F1或F5的方向
B.沿F2或F4的方向
C.沿F2的方向
D.不在MN曲线所确定的水平面内
√
图2
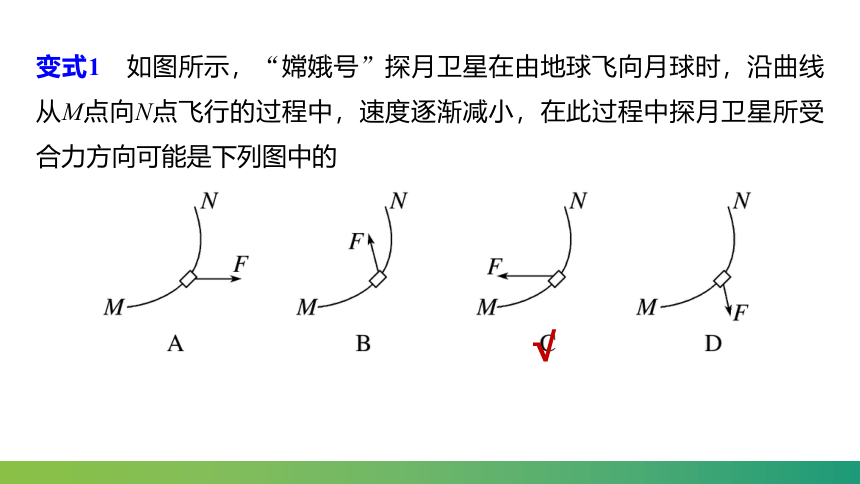
变式1 如图所示,“嫦娥号”探月卫星在由地球飞向月球时,沿曲线从M点向N点飞行的过程中,速度逐渐减小,在此过程中探月卫星所受合力方向可能是下列图中的
√
1.分运动与合运动的关系
等时性 各个分运动与合运动总是同时开始,同时结束,经历时间相等(不同时的运动不能合成)
等效性 各分运动叠加起来与合运动有完全相同的效果
独立性 一个物体同时参与几个分运动时,各分运动独立进行,互不影响
2.运动的合成与分解的运算法则
运动的合成与分解是指描述运动的各物理量,即位移、速度、加速度的合成与分解,由于它们均是矢量,故合成与分解都遵守平行四边形定则。
二、运动的合成与分解
F合(a) 跟 v 在同一直线上
直线运动
F合(a) 恒定→匀变速直线运动
F合(a) 变化→变加速直线运动
F合(a) 跟 v 不在同一直线上
曲线运动
F合(a) 恒定→匀变速曲线运动
F合(a) 变化→变加速曲线运动
3.合运动的性质判断
例3 (2015·广东理综·14)如图所示,帆板在海面上以速度v朝正西方向运动,帆船以速度v朝正北方向航行,以帆板为参照物
A.帆船朝正东方向航行,速度大小为v
B.帆船朝正西方向航行,速度大小为v
C.帆船朝南偏东45°方向航行,速度大小为 v
D.帆船朝北偏东45°方向航行,速度大小为 v
√
解析 以帆板为参照物,帆船具有正东方向的速度v和正北方向的速度v,所以帆船相对帆板的速度v相对= v,方向为北偏东45°,D正确.
变式2 (多选)如图甲所示,在杂技表演中,猴子沿竖直杆向上运动,其v-t图象如图乙所示,同时人顶着杆沿水平地面运动的x-t图象如图丙所示.若以地面为参考系,下列说法正确的是
A.猴子的运动轨迹为直线
B.猴子在2 s内做匀变速曲线运动
C.t=0时猴子的速度大小为8 m/s
D.猴子在2 s内的加速度大小为4 m/s2
√
√
最短时间
最短位移
三、小船渡河模型
分析思路
例4. 小船匀速横渡一条河流,当船头垂直对岸方向航行时,在出发后10 min到达对岸下游120 m处;若船头保持与河岸成α角向上游航行,出发后12.5 min到达正对岸。求:
(1)水流的速度;
(2)小船在静水中的速度、河的宽度以及船头与河岸间的夹角α。
1.模型特点
沿绳(杆)方向的速度分量大小相等。
2.思路与方法
合速度→绳(杆)拉物体的实际运动速度v
方法:v∥与v⊥的合成遵循平行四边形定则。
3.解题原则:根据沿绳(杆)方向的分速度大小相等求解。常见实例如图:
四、速度关联问题
例5.如图所示,不计所有接触面之间的摩擦,斜面固定,物块和滑块质量分别为m1和m2,且m1<m2。若将滑块从位置A由静止释放,当沿杆落到位置B时,滑块的速度为v2,且与滑块牵连的绳子与竖直方向的夹角为θ,则此时物块的速度大小v1等于( )
【解析】 物块的速度与绳上各点沿绳方向的速度大小相等,所以绳的速度等于物块的速度v1。滑块的实际运动是沿杆竖直下滑,这个实际运动是合运动,合速度v2可分解为沿绳方向的分速度和垂直于绳方向的分速度。因此v1与v2的关系如图所示,由图可看出物块的速度大小v1=v2cos θ,所以选项C正确。
五、平抛运动基本规律的应用
速度改变量
因为平抛运动的加速度为恒定的重力加速度g,所以做平抛运动的物体在任意相等时间间隔Δt内的速度改变量Δv=gΔt是相同的,方向恒为竖直向下,如图所示.
两个重要推论
(1)做平抛运动的物体在任意时刻的瞬时速度的反向延长线一定通过此时水平位移的中点,如图所示,即xB=
推导:
(2)做平抛运动的物体在任意时刻任意位置处,有tan θ=2tan α.
推导:
例6 如图所示,A、B两个小球在同一竖直线上,离地高度分别为2h和h,将两球水平抛出后,两球落地时的水平位移之比为1∶2,则下列说法正确的是 ( )
√
运动情形 分析方法 运动规律 飞行时间
从空中抛出垂直落到斜面上 分解速度,构建速度的矢量三角形 水平方向:vx=v0 竖直方向:vy=gt θ与v0、t的关系:
从斜面抛出又落到斜面上 分解位移,构建位移的矢量三角形 水平方向:x=v0t 竖直方向: θ与v0、t的关系:
与斜面有关的平抛运动,两种情况的特点及分析方法对比如下:
六、与斜面有关的平抛运动
例7.如图所示,一个倾角为37°的斜面固定在水平面上,在斜面底端正上方的O点将一小球以速度v0=3 m/s水平抛出,经过一段时间后,小球垂直斜面打在P点处(小球可视为质点,不计空气阻力,取重力加速度g=10 m/s2,sin 37°=0.6,cos 37°=0.8),则
A.小球击中斜面时的速度大小为5 m/s
B.小球击中斜面时的速度大小为4 m/s
C.小球做平抛运动的水平位移是1.6 m
D.小球做平抛运动的竖直位移是1 m
√
例8.如图4所示,两个相对的斜面的倾角分别为37°和53°,在斜面顶点把两个小球以同样大小的初速度分别向左、向右水平抛出,小球都落在斜面上.若不计空气阻力,则A、B两个小球的运动时间之比为
A.1∶1 B.1∶3 C.16∶9 D.9∶16
√
常见的“三种”临界特征
(1)有些题目中有“刚好”“恰好”“正好”等字眼,明显表明题述的过程中存在着临界点。
(2)若题目中有“取值范围”“多长时间”“多大距离”等词语,表明题述的过程中存在着“起止点”,而这些起止点往往就是临界点。
(3)若题目中有“最大”“最小”“至多”“至少”等字眼,表明题述的过程中存在着极值,这个极值点往往是临界点。
求解平抛运动临界问题的一般思路
(1)确定临界状态。 (2)找出临界状态对应的临界条件。
(3)分解速度或位移。 (4)若有必要,画出临界轨迹。
七.平抛运动中临界问题的分析方法
例9.一阶梯如图所示,其中每级台阶的高度和宽度都是0.4 m,一小球以水平速度v从图示位置飞出,不计空气阻力,g取10 m/s2,欲打在第4级台阶上,则v的取值范围是
√
例10.一带有乒乓球发射机的乒乓球台如图所示.水平台面的长和宽分别为L1和L2,中间球网高度为h.发射机安装于台面左侧边缘的中点,能以不同速率向右侧不同方向水平发射乒乓球,发射点距台面高度为3h.不计空气的作用,重力加速度大小为g.若乒乓球的发射速率v在某范围内,通过选择合适的方向,就能使乒乓球落到球网右侧台面上,则v的最大取值范围是( )
√
人教版(2019)高中物理必修第二册
第五章 抛体运动
章 末 复 习
授课人:扬帆起航
知识网络
知识网络
知识网络
课堂练习
判一判
(1)做曲线运动的物体速度大小一定发生变化.( )
(2)做曲线运动的物体加速度一定是变化的.( )
(3)曲线运动一定是变速运动.( )
(4)两个分运动的时间一定与它们合运动的时间等( )
(5)合运动的速度一定大于分运动的速度.( )
(6)两个直线运动的合运动一定是直线运动.( )
(1)×(2)×(3)√(4)√(5)×(6)×
考向一 物体做曲线运动的条件及轨迹分析
1.运动轨迹的判断
(1)若物体所受合力方向与速度方向在同一直线上,则物体做直线运动。
(2)若物体所受合力方向与速度方向不在同一直线上,则物体做曲线运动。
2.合力方向与速率变化的关系
一、曲线运动的条件和特征
3.两个直线运动的合运动性质的判断
标准:看合初速度方向与合加速度方向是否共线.
两个互成角度的分运动 合运动的性质
两个匀速直线运动 匀速直线运动
一个匀速直线运动、一个匀变速直线运动 运动
两个初速度为零的匀加速直线运动 运动
两个初速度不为零的匀变速直线运动 如果v合与a合共线,为_______
运动
如果v合与a合不共线,为_____
运动
匀变速曲线
匀加速直线
匀变速
直线
匀变
速曲线
根据下列规律做出判断:
例1 下列说法正确的是
A.做曲线运动的物体的速度一定变化
B.速度变化的运动一定是曲线运动
C.加速度恒定的运动不可能是曲线运动
D.加速度变化的运动一定是曲线运动
√
解析 做曲线运动的物体,速度方向一定改变,选项A正确;速度大小改变而方向不变的运动是直线运动,选项B错误;平抛运动是加速度恒定的曲线运动,选项C错误;加速度大小改变,但加速度方向与速度方向始终相同,这种运动是直线运动,选项D错误.
例2 一个物体在光滑水平面上沿曲线MN运动,如图2所示,其中A点是曲线上的一点,虚线1、2分别是过A点的切线和法线,已知该过程中物体所受的合外力是恒力,则当物体运动到A点时,合外力的方向可能是
A.沿F1或F5的方向
B.沿F2或F4的方向
C.沿F2的方向
D.不在MN曲线所确定的水平面内
√
图2
变式1 如图所示,“嫦娥号”探月卫星在由地球飞向月球时,沿曲线从M点向N点飞行的过程中,速度逐渐减小,在此过程中探月卫星所受合力方向可能是下列图中的
√
1.分运动与合运动的关系
等时性 各个分运动与合运动总是同时开始,同时结束,经历时间相等(不同时的运动不能合成)
等效性 各分运动叠加起来与合运动有完全相同的效果
独立性 一个物体同时参与几个分运动时,各分运动独立进行,互不影响
2.运动的合成与分解的运算法则
运动的合成与分解是指描述运动的各物理量,即位移、速度、加速度的合成与分解,由于它们均是矢量,故合成与分解都遵守平行四边形定则。
二、运动的合成与分解
F合(a) 跟 v 在同一直线上
直线运动
F合(a) 恒定→匀变速直线运动
F合(a) 变化→变加速直线运动
F合(a) 跟 v 不在同一直线上
曲线运动
F合(a) 恒定→匀变速曲线运动
F合(a) 变化→变加速曲线运动
3.合运动的性质判断
例3 (2015·广东理综·14)如图所示,帆板在海面上以速度v朝正西方向运动,帆船以速度v朝正北方向航行,以帆板为参照物
A.帆船朝正东方向航行,速度大小为v
B.帆船朝正西方向航行,速度大小为v
C.帆船朝南偏东45°方向航行,速度大小为 v
D.帆船朝北偏东45°方向航行,速度大小为 v
√
解析 以帆板为参照物,帆船具有正东方向的速度v和正北方向的速度v,所以帆船相对帆板的速度v相对= v,方向为北偏东45°,D正确.
变式2 (多选)如图甲所示,在杂技表演中,猴子沿竖直杆向上运动,其v-t图象如图乙所示,同时人顶着杆沿水平地面运动的x-t图象如图丙所示.若以地面为参考系,下列说法正确的是
A.猴子的运动轨迹为直线
B.猴子在2 s内做匀变速曲线运动
C.t=0时猴子的速度大小为8 m/s
D.猴子在2 s内的加速度大小为4 m/s2
√
√
最短时间
最短位移
三、小船渡河模型
分析思路
例4. 小船匀速横渡一条河流,当船头垂直对岸方向航行时,在出发后10 min到达对岸下游120 m处;若船头保持与河岸成α角向上游航行,出发后12.5 min到达正对岸。求:
(1)水流的速度;
(2)小船在静水中的速度、河的宽度以及船头与河岸间的夹角α。
1.模型特点
沿绳(杆)方向的速度分量大小相等。
2.思路与方法
合速度→绳(杆)拉物体的实际运动速度v
方法:v∥与v⊥的合成遵循平行四边形定则。
3.解题原则:根据沿绳(杆)方向的分速度大小相等求解。常见实例如图:
四、速度关联问题
例5.如图所示,不计所有接触面之间的摩擦,斜面固定,物块和滑块质量分别为m1和m2,且m1<m2。若将滑块从位置A由静止释放,当沿杆落到位置B时,滑块的速度为v2,且与滑块牵连的绳子与竖直方向的夹角为θ,则此时物块的速度大小v1等于( )
【解析】 物块的速度与绳上各点沿绳方向的速度大小相等,所以绳的速度等于物块的速度v1。滑块的实际运动是沿杆竖直下滑,这个实际运动是合运动,合速度v2可分解为沿绳方向的分速度和垂直于绳方向的分速度。因此v1与v2的关系如图所示,由图可看出物块的速度大小v1=v2cos θ,所以选项C正确。
五、平抛运动基本规律的应用
速度改变量
因为平抛运动的加速度为恒定的重力加速度g,所以做平抛运动的物体在任意相等时间间隔Δt内的速度改变量Δv=gΔt是相同的,方向恒为竖直向下,如图所示.
两个重要推论
(1)做平抛运动的物体在任意时刻的瞬时速度的反向延长线一定通过此时水平位移的中点,如图所示,即xB=
推导:
(2)做平抛运动的物体在任意时刻任意位置处,有tan θ=2tan α.
推导:
例6 如图所示,A、B两个小球在同一竖直线上,离地高度分别为2h和h,将两球水平抛出后,两球落地时的水平位移之比为1∶2,则下列说法正确的是 ( )
√
运动情形 分析方法 运动规律 飞行时间
从空中抛出垂直落到斜面上 分解速度,构建速度的矢量三角形 水平方向:vx=v0 竖直方向:vy=gt θ与v0、t的关系:
从斜面抛出又落到斜面上 分解位移,构建位移的矢量三角形 水平方向:x=v0t 竖直方向: θ与v0、t的关系:
与斜面有关的平抛运动,两种情况的特点及分析方法对比如下:
六、与斜面有关的平抛运动
例7.如图所示,一个倾角为37°的斜面固定在水平面上,在斜面底端正上方的O点将一小球以速度v0=3 m/s水平抛出,经过一段时间后,小球垂直斜面打在P点处(小球可视为质点,不计空气阻力,取重力加速度g=10 m/s2,sin 37°=0.6,cos 37°=0.8),则
A.小球击中斜面时的速度大小为5 m/s
B.小球击中斜面时的速度大小为4 m/s
C.小球做平抛运动的水平位移是1.6 m
D.小球做平抛运动的竖直位移是1 m
√
例8.如图4所示,两个相对的斜面的倾角分别为37°和53°,在斜面顶点把两个小球以同样大小的初速度分别向左、向右水平抛出,小球都落在斜面上.若不计空气阻力,则A、B两个小球的运动时间之比为
A.1∶1 B.1∶3 C.16∶9 D.9∶16
√
常见的“三种”临界特征
(1)有些题目中有“刚好”“恰好”“正好”等字眼,明显表明题述的过程中存在着临界点。
(2)若题目中有“取值范围”“多长时间”“多大距离”等词语,表明题述的过程中存在着“起止点”,而这些起止点往往就是临界点。
(3)若题目中有“最大”“最小”“至多”“至少”等字眼,表明题述的过程中存在着极值,这个极值点往往是临界点。
求解平抛运动临界问题的一般思路
(1)确定临界状态。 (2)找出临界状态对应的临界条件。
(3)分解速度或位移。 (4)若有必要,画出临界轨迹。
七.平抛运动中临界问题的分析方法
例9.一阶梯如图所示,其中每级台阶的高度和宽度都是0.4 m,一小球以水平速度v从图示位置飞出,不计空气阻力,g取10 m/s2,欲打在第4级台阶上,则v的取值范围是
√
例10.一带有乒乓球发射机的乒乓球台如图所示.水平台面的长和宽分别为L1和L2,中间球网高度为h.发射机安装于台面左侧边缘的中点,能以不同速率向右侧不同方向水平发射乒乓球,发射点距台面高度为3h.不计空气的作用,重力加速度大小为g.若乒乓球的发射速率v在某范围内,通过选择合适的方向,就能使乒乓球落到球网右侧台面上,则v的最大取值范围是( )
√
