第五章 专题 关联速度的问题(课件)-2021-2022学年【扬帆起航系列】人教版(2019)高中物理课件必修第二册(共22张PPT)
文档属性
| 名称 | 第五章 专题 关联速度的问题(课件)-2021-2022学年【扬帆起航系列】人教版(2019)高中物理课件必修第二册(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-12-06 14:56:43 | ||
图片预览





文档简介
(共21张PPT)
人教版(2019)高中物理必修第二册
第五章 抛体运动
专题 关联速度的分解问题
授课人:扬帆起航
关联体一般是两个(或两个以上)物体通过不可伸长的轻绳或轻杆联系在一起或直接挤压到一起,它们的运动简称为关联运动。
相互关联的两个物体一般不是都沿轻绳或轻杆运动的,从而使两个物体的速度不相同,有时两个物体即使在同一方向上运动,其速度的大小也不相等,但二者的速度存在某种关系,此二者的速度称为“关联速度”.
关联速度
在运动过程中,绳、杆等有长度的物体,其两端点的速度通常是不一样的,但两端点的速度是有联系的,我们称之为“关联速度”,解决关联速度的关键 :
(1)物体的实际运动(速度)一定是合运动(速度),分速度的方向要按实际运动效果确定。即一般分解时两个分速度方向应取沿绳(或杆)方向和垂直绳(或杆)方向.
(2)由于绳(或杆)不可伸长,沿绳(或杆)方向的分速度大小相等.
(1)确定合运动的方向:物体运动的实际方向就是合运动的方向,即合速度的方向.
(2)确定合运动的两个效果.
轻绳或可自由转动的轻杆连接物体的问题
效果1:沿绳或杆方向运动;
效果2:垂直绳或杆方向运动.
相互接触物体的问题
效果1:垂直于接触面的运动;
效果2:沿接触面的运动.
(3)画出合运动与分运动遵循的平行四边形定则,确定它们的大小关系.
关联速度问题求解步骤:
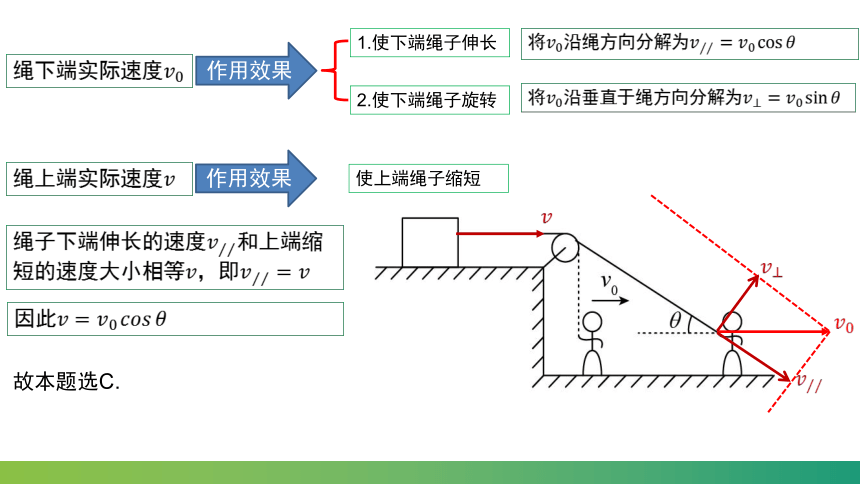
例1.如图所示,物体放在水平平台上,系在物体上的绳子跨过定滑轮,由地面上的人以速度向右水平匀速拉动,设人从地面上平台的边缘开始向右行至绳与水平方向夹角为30°处,此时物体的速度为( )
A. B. C. D.
典例精讲
绳下端实际速度
1.使下端绳子伸长
2.使下端绳子旋转
将沿绳方向分解为
将沿垂直于绳方向分解为
绳上端实际速度
使上端绳子缩短
作用效果
作用效果
绳子下端伸长的速度和上端缩短的速度大小相等,即
因此
故本题选C.
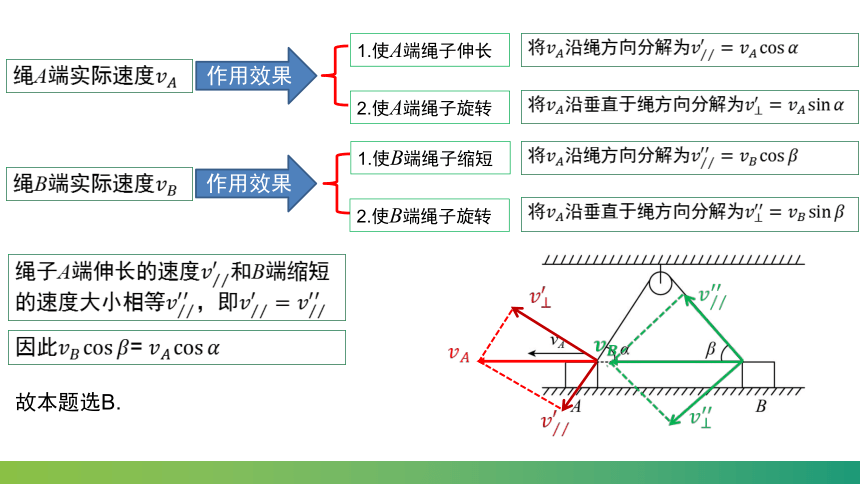
例2.一根细绳通过定滑轮且两端分别系着A和B两物体,如图所示,物体A在外力作用下,向左以vA匀速运动,当连A的绳子与水平方向成a角,连B的绳子与水平方向成角时,B物体的速度为vB,则( )
A.A物体的速度vA与B物体的速度vB的大小相等
B.A物体的速度vA与B物体的速度vB的大小关系满足
C.此后B物体以速度vB做匀速运动
D.此后B物体的速度越来越大,所以做减速运动
典例精讲
绳A端实际速度
1.使A端绳子伸长
2.使A端绳子旋转
将沿绳方向分解为
将沿垂直于绳方向分解为
绳B端实际速度
1.使B端绳子缩短
作用效果
作用效果
绳子A端伸长的速度和B端缩短的速度大小相等,即
因此=
故本题选B.
2.使B端绳子旋转
将沿绳方向分解为
将沿垂直于绳方向分解为
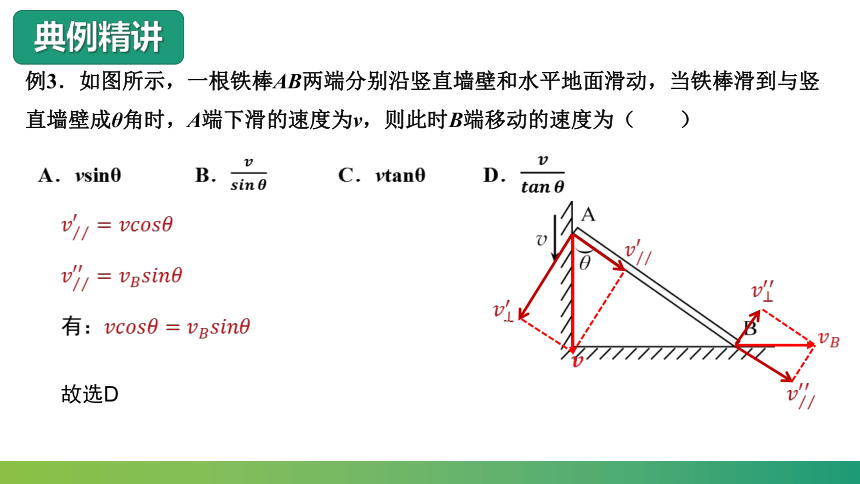
例3.如图所示,一根铁棒AB两端分别沿竖直墙壁和水平地面滑动,当铁棒滑到与竖直墙壁成θ角时,A端下滑的速度为v,则此时B端移动的速度为( )
A.vsinθ B. C.vtanθ D.
有:
故选D
典例精讲
例4.如图,长为L的直棒一端可绕固定轴O在竖直平面内转动,另一端搁在升降平台上,平台以速度v匀速上升,当棒与竖直方向的夹角为θ时,棒的瞬时速率为( )
A. B. C. D.
故选B
典例精讲
θ
v1
v2
v
沿绳方向使绳伸长
垂直于绳方向使绳转动
绳(杆)模型绳(杆)端速度分解原则:
沿着绳(杆)和垂直绳(杆)
则V与V1的关系为 ?
注:绳(杆)两端速度大小一般不相等,但两端沿绳(杆)方向速度一定相等※
V1=VCOSθ
“绳+物”问题
如图所示,绳子以恒定速率v 沿水平方向通过定滑轮牵引小船靠岸,当绳子与水面夹角为θ时,船的速度为多大?
v
θ
A
B
C
v∥
v⊥
v船
【解析】1.沿绳子方向两个绳连接的物体沿绳子方向的速度大小相等( v∥ =v )。
2.当绳与物体运动方向有夹角时,沿绳子方向和垂直绳子方向速度为分速度.
物体运动的方向为合速度方向。
v船 =v/cosθ
“绳+物”问题
“绳+物”问题
【例题】如图所示,A、B两物体用细绳相连,在水平面上运动,当α=450,β=300时,物体A的速度为2 m/s,这时B的速度为 。
寻找分运动效果
【答案】
“杆+物”问题
【例题】如图所示,杆AB它的两端在地板和竖直墙壁上,现拉A端由图示位置以速率v匀速向右运动,B端滑动的速度是 。
寻找分运动效果
α
Vcosθ
VBcosα
【例题】如图所示,滑块B以速度vB向左运动时,触点P的沿杆移动的速度如何?
【答案】
寻找分运动效果
“杆+物”问题
常见的速度分解模型
1.如图所示,套在竖直细杆上的轻环A由跨过定滑轮的不可伸长的轻绳与重物B相连,施加外力让A沿杆以速度v匀速上升,从图中M位置上升至与定滑轮的连线处于水平N位置,已知AO与竖直杆成角,则( )
A.A匀速上升时,重物B加速下降
B.重物B下降过程,绳对B的拉力小于B的重力
C.刚开始时B的速度vB=vcosθ
D.刚开始时B的速度vB=
随堂练习
解析:CD.对于A,它的速度如图中标出的v,这个速度看成是A的合速度,其分速度分别是va、vb,其中va就是B的速率(同一根绳子,大小相同),故A刚开始上升时B的速度vB=vcosθ,故C正确,D错误。
AB.由vB=vcosθ可知,由于A匀速上升,θ在增大,所以vB在减小,当运动至定滑轮的连线处于水平位置时θ=90°,vB=0B做减速运动,处于超重状态,绳对B的拉力大于B的重力,故AB错误;
故选C。
2.如图所示,A、B两物体系在跨过光滑定滑轮的一根轻绳的两端,当A物体以速度v向左运动时,系A、B的绳分别与水平方向成α、β角,此时B物体的速度大小为( )
A. B. C. D.
解析:将A物体的速度沿着绳子方向与垂直绳子方向进行分解,如图所示,则A在沿绳方向的速度大小为;设B物体的速度为,将B物体的速度沿着绳子方向与垂直绳子方向进行分解,则B在沿着绳子方向的速度大小为,由于沿着绳子方向速度大小相等,所以有,
因此,且方向向右。故选D。
随堂练习
3.2021年3月11号宁夏银川,一家餐厅后厨起火后,厨师和餐馆负责人却先跑了,三名顾客被困。大火被扑灭后,三人被救出。两人因未尽到组织引导顾客疏散的义务被刑拘。火灾逃生的首要原则是离开火灾现场,如图是火警设计的一种快捷让当事人逃离现场的救援方案:用一根不变形的轻杆MN支撑在楼面平台AB上,N端在水平地面上向右以v0匀速运动,被救助的人员紧抱在M端随轻杆向平台B端靠近,平台高h,当BN=2h时,则此时被救人员向B点运动的速率是( )
A.v0 B.2v0 C. D.
解析:设杆与水平面CD的夹角为,由几何关系可知
即;将杆上N点的速度分解成沿杆的分速度和垂直杆转动的速度 ,由矢量三角形可知;而沿着同一根杆,各点的速度相同,故被救人员向B点运动的速率为,故选C。
随堂练习
4.光滑半球A放在竖直面光滑的墙角,并用手推着保持静止.现在A与墙壁之间放入光滑球B,放手让A和B由静止开始运动,当A、B运动到图示位置时,二者球心的连线与水平面成θ角,速度大小分别为和,则以下关系正确的是( )
A. B. C. D.
解析:将A、B两球的速度沿两球心的连线和垂直两球心连线分解,如图,由关联速度的关系可得:,解得:,故D正确.
随堂练习
人教版(2019)高中物理必修第二册
第五章 抛体运动
专题 关联速度的分解问题
授课人:扬帆起航
关联体一般是两个(或两个以上)物体通过不可伸长的轻绳或轻杆联系在一起或直接挤压到一起,它们的运动简称为关联运动。
相互关联的两个物体一般不是都沿轻绳或轻杆运动的,从而使两个物体的速度不相同,有时两个物体即使在同一方向上运动,其速度的大小也不相等,但二者的速度存在某种关系,此二者的速度称为“关联速度”.
关联速度
在运动过程中,绳、杆等有长度的物体,其两端点的速度通常是不一样的,但两端点的速度是有联系的,我们称之为“关联速度”,解决关联速度的关键 :
(1)物体的实际运动(速度)一定是合运动(速度),分速度的方向要按实际运动效果确定。即一般分解时两个分速度方向应取沿绳(或杆)方向和垂直绳(或杆)方向.
(2)由于绳(或杆)不可伸长,沿绳(或杆)方向的分速度大小相等.
(1)确定合运动的方向:物体运动的实际方向就是合运动的方向,即合速度的方向.
(2)确定合运动的两个效果.
轻绳或可自由转动的轻杆连接物体的问题
效果1:沿绳或杆方向运动;
效果2:垂直绳或杆方向运动.
相互接触物体的问题
效果1:垂直于接触面的运动;
效果2:沿接触面的运动.
(3)画出合运动与分运动遵循的平行四边形定则,确定它们的大小关系.
关联速度问题求解步骤:
例1.如图所示,物体放在水平平台上,系在物体上的绳子跨过定滑轮,由地面上的人以速度向右水平匀速拉动,设人从地面上平台的边缘开始向右行至绳与水平方向夹角为30°处,此时物体的速度为( )
A. B. C. D.
典例精讲
绳下端实际速度
1.使下端绳子伸长
2.使下端绳子旋转
将沿绳方向分解为
将沿垂直于绳方向分解为
绳上端实际速度
使上端绳子缩短
作用效果
作用效果
绳子下端伸长的速度和上端缩短的速度大小相等,即
因此
故本题选C.
例2.一根细绳通过定滑轮且两端分别系着A和B两物体,如图所示,物体A在外力作用下,向左以vA匀速运动,当连A的绳子与水平方向成a角,连B的绳子与水平方向成角时,B物体的速度为vB,则( )
A.A物体的速度vA与B物体的速度vB的大小相等
B.A物体的速度vA与B物体的速度vB的大小关系满足
C.此后B物体以速度vB做匀速运动
D.此后B物体的速度越来越大,所以做减速运动
典例精讲
绳A端实际速度
1.使A端绳子伸长
2.使A端绳子旋转
将沿绳方向分解为
将沿垂直于绳方向分解为
绳B端实际速度
1.使B端绳子缩短
作用效果
作用效果
绳子A端伸长的速度和B端缩短的速度大小相等,即
因此=
故本题选B.
2.使B端绳子旋转
将沿绳方向分解为
将沿垂直于绳方向分解为
例3.如图所示,一根铁棒AB两端分别沿竖直墙壁和水平地面滑动,当铁棒滑到与竖直墙壁成θ角时,A端下滑的速度为v,则此时B端移动的速度为( )
A.vsinθ B. C.vtanθ D.
有:
故选D
典例精讲
例4.如图,长为L的直棒一端可绕固定轴O在竖直平面内转动,另一端搁在升降平台上,平台以速度v匀速上升,当棒与竖直方向的夹角为θ时,棒的瞬时速率为( )
A. B. C. D.
故选B
典例精讲
θ
v1
v2
v
沿绳方向使绳伸长
垂直于绳方向使绳转动
绳(杆)模型绳(杆)端速度分解原则:
沿着绳(杆)和垂直绳(杆)
则V与V1的关系为 ?
注:绳(杆)两端速度大小一般不相等,但两端沿绳(杆)方向速度一定相等※
V1=VCOSθ
“绳+物”问题
如图所示,绳子以恒定速率v 沿水平方向通过定滑轮牵引小船靠岸,当绳子与水面夹角为θ时,船的速度为多大?
v
θ
A
B
C
v∥
v⊥
v船
【解析】1.沿绳子方向两个绳连接的物体沿绳子方向的速度大小相等( v∥ =v )。
2.当绳与物体运动方向有夹角时,沿绳子方向和垂直绳子方向速度为分速度.
物体运动的方向为合速度方向。
v船 =v/cosθ
“绳+物”问题
“绳+物”问题
【例题】如图所示,A、B两物体用细绳相连,在水平面上运动,当α=450,β=300时,物体A的速度为2 m/s,这时B的速度为 。
寻找分运动效果
【答案】
“杆+物”问题
【例题】如图所示,杆AB它的两端在地板和竖直墙壁上,现拉A端由图示位置以速率v匀速向右运动,B端滑动的速度是 。
寻找分运动效果
α
Vcosθ
VBcosα
【例题】如图所示,滑块B以速度vB向左运动时,触点P的沿杆移动的速度如何?
【答案】
寻找分运动效果
“杆+物”问题
常见的速度分解模型
1.如图所示,套在竖直细杆上的轻环A由跨过定滑轮的不可伸长的轻绳与重物B相连,施加外力让A沿杆以速度v匀速上升,从图中M位置上升至与定滑轮的连线处于水平N位置,已知AO与竖直杆成角,则( )
A.A匀速上升时,重物B加速下降
B.重物B下降过程,绳对B的拉力小于B的重力
C.刚开始时B的速度vB=vcosθ
D.刚开始时B的速度vB=
随堂练习
解析:CD.对于A,它的速度如图中标出的v,这个速度看成是A的合速度,其分速度分别是va、vb,其中va就是B的速率(同一根绳子,大小相同),故A刚开始上升时B的速度vB=vcosθ,故C正确,D错误。
AB.由vB=vcosθ可知,由于A匀速上升,θ在增大,所以vB在减小,当运动至定滑轮的连线处于水平位置时θ=90°,vB=0B做减速运动,处于超重状态,绳对B的拉力大于B的重力,故AB错误;
故选C。
2.如图所示,A、B两物体系在跨过光滑定滑轮的一根轻绳的两端,当A物体以速度v向左运动时,系A、B的绳分别与水平方向成α、β角,此时B物体的速度大小为( )
A. B. C. D.
解析:将A物体的速度沿着绳子方向与垂直绳子方向进行分解,如图所示,则A在沿绳方向的速度大小为;设B物体的速度为,将B物体的速度沿着绳子方向与垂直绳子方向进行分解,则B在沿着绳子方向的速度大小为,由于沿着绳子方向速度大小相等,所以有,
因此,且方向向右。故选D。
随堂练习
3.2021年3月11号宁夏银川,一家餐厅后厨起火后,厨师和餐馆负责人却先跑了,三名顾客被困。大火被扑灭后,三人被救出。两人因未尽到组织引导顾客疏散的义务被刑拘。火灾逃生的首要原则是离开火灾现场,如图是火警设计的一种快捷让当事人逃离现场的救援方案:用一根不变形的轻杆MN支撑在楼面平台AB上,N端在水平地面上向右以v0匀速运动,被救助的人员紧抱在M端随轻杆向平台B端靠近,平台高h,当BN=2h时,则此时被救人员向B点运动的速率是( )
A.v0 B.2v0 C. D.
解析:设杆与水平面CD的夹角为,由几何关系可知
即;将杆上N点的速度分解成沿杆的分速度和垂直杆转动的速度 ,由矢量三角形可知;而沿着同一根杆,各点的速度相同,故被救人员向B点运动的速率为,故选C。
随堂练习
4.光滑半球A放在竖直面光滑的墙角,并用手推着保持静止.现在A与墙壁之间放入光滑球B,放手让A和B由静止开始运动,当A、B运动到图示位置时,二者球心的连线与水平面成θ角,速度大小分别为和,则以下关系正确的是( )
A. B. C. D.
解析:将A、B两球的速度沿两球心的连线和垂直两球心连线分解,如图,由关联速度的关系可得:,解得:,故D正确.
随堂练习
