青岛版三 剪纸中的数学-分数加减法(一)信息窗2 同分母分数加减法 课件(共36张PPT)
文档属性
| 名称 | 青岛版三 剪纸中的数学-分数加减法(一)信息窗2 同分母分数加减法 课件(共36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 12:34:31 | ||
图片预览








文档简介
(共36张PPT)
同分母分数加减法
青岛版数学五年级(下)
三 剪纸中的数学
——分数的加减法(一)
1.理解分数加减法的意义,初步掌握同分母分数加减法的算理和计算法则。
2.结合情景了解约分的意义,掌握约分的方法。
3.使学生在新知的探索中,体验学习和探索的乐趣,培养学生学好数学的信心及团队协作能力。
学习目标
【重点】
同分母分数加减法的算理和计算法则。
【难点】
约分的方法。
你能提出哪些数学问题?
课堂导入
我吃了 。
1
9
我吃了 。
4
9
蝴 蝶
鲤鱼
1
8
3
8
你还能提出什么问题?
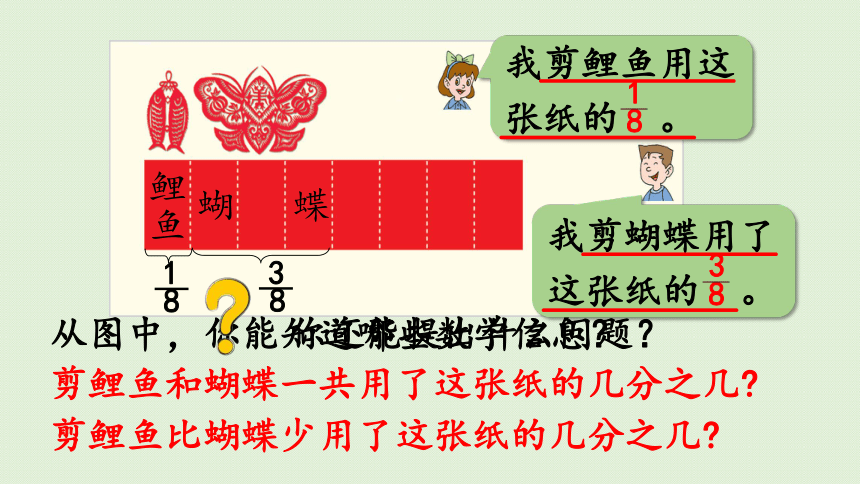
从图中,你能知道哪些数学信息?
剪鲤鱼和蝴蝶一共用了这张纸的几分之几
剪鲤鱼比蝴蝶少用了这张纸的几分之几
我剪鲤鱼用这张纸的 。
1
8
我剪蝴蝶用了这张纸的 。
3
8
新知探究
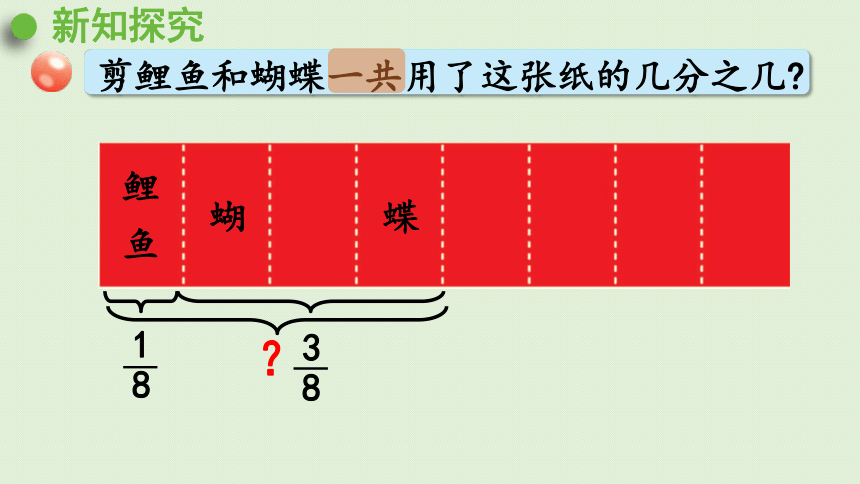
剪鲤鱼和蝴蝶一共用了这张纸的几分之几
鲤 鱼
蝴 蝶
1
8
3
8
?
1个 加3个 是
4个 ,就是 ,
所以 + = 。
1
8
1
8
4
8
1
8
3
8
1
8
4
8
根据分数的基本性质可以把得数化成更简单的分数:
1
2
÷
=
=
4
8
8
4
÷
4
4
+ =
=
1
8
3
8
1+3
8
4
8
答:剪鲤鱼和蝴蝶一共用了这张纸的 。
1
2
1
2
=
剪鲤鱼和蝴蝶一共用了这张纸的几分之几
把一个分数化成同它相等,但分子、分母都
比较小的分数,叫作约分。
8
1
=
+
8
3
8
1+3
8
4
=
1
2
=
2
1
分母不变
分子相加
不是最简分数
约成最简分数
分数加法的意义和整数加法的意义相同,都是把两个数合并成一个数的运算。
你会把 约分吗?
12
18
9
6
2
18
2
12
18
12
÷
÷
=
=
分别除以分子和分母的公因数2。
9
6
2
18
2
12
18
12
÷
÷
=
=
3
2
3
9
3
6
9
6
÷
÷
=
=
分子和分母先
分别除以公因数2,再除以公因数3。
小丽
小红
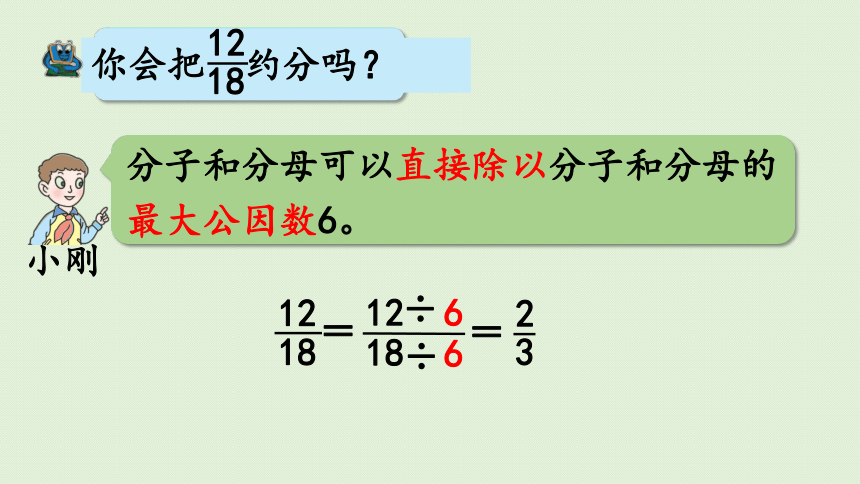
你会把 约分吗?
12
18
分子和分母可以直接除以分子和分母的最大公因数6。
3
2
6
18
6
12
18
12
÷
÷
=
=
小刚
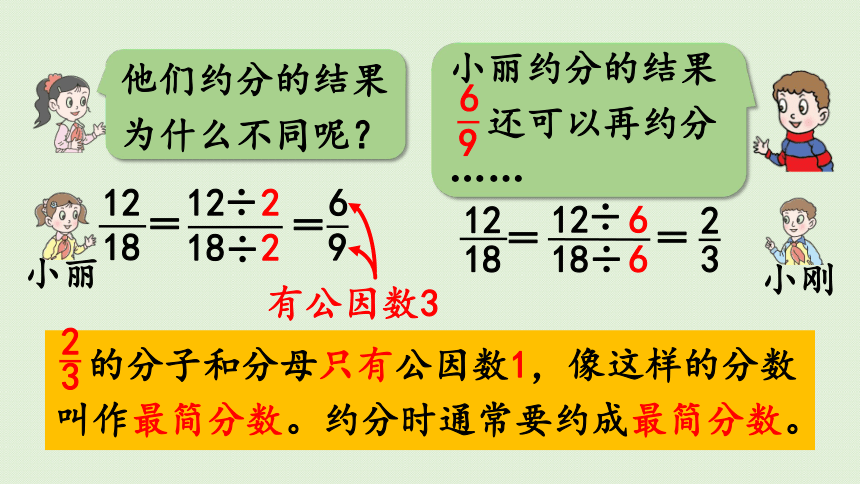
他们约分的结果为什么不同呢?
9
6
2
18
2
12
18
12
÷
÷
=
=
3
2
6
18
6
12
18
12
÷
÷
=
=
小刚
小丽
小丽约分的结果
还可以再约分
……
9
6
有公因数3
的分子和分母只有公因数1,像这样的分数叫作最简分数。约分时通常要约成最简分数。
3
2
约分可以写成下面的形式。
18
12
=
18
12
6
9
2
3
3
2
=
18
12
=
18
12
2
3
3
2
=
先分别除以18和12的公因数2。
再分别除以6和9的公因数3。
也可以分别除以18和12的最大公因数6。
或直接写成
18
12
=
3
2
逐步约分法
一次约分法
剪蝴蝶比剪鲤鱼多用了这张纸的几分之几?
鲤 鱼
蝴 蝶
1
8
3
8
?
3个 减1个 是
2个 ,就是 ,
所以 - = 。
1
8
1
8
2
8
1
8
1
8
3
8
2
8
剪蝴蝶比剪鲤鱼多用了这张纸的几分之几?
剪蝴蝶比剪鲤鱼多用了这张纸的几分之几?
8
3
-
=
8
1
8
2
=
4
1
1
4
计算结果能约分,一般要约成最简分数。
答:剪蝴蝶比剪鲤鱼多用了这张纸的 。
4
1
剪蝴蝶比剪鲤鱼多用了这张纸的几分之几?
8
3-1
=
8
3
=
-
8
1
8
3-1
8
2
=
1
4
=
4
1
分母不变
分子相减
不是最简分数
约成最简分数
分数减法的意义和整数减法的意义相同,都是已知两个数的和与其中一个加数,求另一个加数的运算。
共同点
8
1
=
+
8
3
8
1+3
8
4
=
1
2
=
2
1
8
3
=
-
8
1
8
3-1
8
2
=
1
4
=
4
1
观察两个算式,你能发现什么共同点吗?
分母相同
①都是分母相同的分数相加、减;
分子相加减
分母不变
②计算时,只把分子相加减,分母不变;
最简分数
③计算结果都是最简分数。
请你概括同分母分数加减法的计算法则。
同分母分数相加、减,分母不变。
只把分子相加、减。
同分母分数加减法的计算法则:分母不变,只把分子相加、减。计算结果能约分的要约成最简分数。
1.填空。
课堂练习
(教材第35页“第1题” )
5
4
30
24
30
24
÷
÷
=
=
6
6
4
3
28
21
28
21
÷
÷
=
=
7
7
9
7
45
72
=
=
35
56
4
12
36
9
=
=
3
1
×5
÷3
×8
÷9
2. 把上下相等的数连一连。
7
3
6
4
5
2
8
6
9
3
21
9
4
3
3
1
25
10
3
2
(教材第35页“第5题” )
21
6
7
4
10
8
5
3
4
1
28
7
12
7
36
3
18
12
5
2
4
3
15
9
2
7
<
4
5
<
1
4
=
1
12
>
2
3
>
3
5
>
3.先化简,再比较下面每组中两个分数的大小。
(2)分数 的分子和分母的最大公因数是( ) ,化成最简分数是( )。
(1)一个分数约分后,分数的大小( )。
4. 填一填。
(3)分母是 8 的最简真分数的和是( )。
不变
3
2
(4)一个最简真分数,分子和分母的积是7,这个分数是( )。
27
6
9
2
7
1
(教材第36页“第6题” )
5. 2012年伦敦奥运会的跳水项目设有8枚金牌,被誉为“梦之队”的中国跳水队夺得了6枚。中国跳水队夺得的金牌数占跳水项目金牌总数的几分之几?
=
6÷8
4
3
答:中国跳水队夺得的金牌数占
跳水项目金牌总数的 。
4
3
6. 在括号里填上最简分数。
40分=( )时
75cm=( )m
20秒=( )分
500千克=( )吨
=( )
35dm=( )m
40÷60=
40
60
2
3
=
3
2
75÷100=
75
100
3
4
=
4
3
20÷60=
20
60
1
3
=
3
1
35÷10=
35
10
7
2
=
2
7
500÷1000=
500
1000
1
2
=
2
1
60÷100=
60
100
3
5
=
5
3
9
2
+
=
9
4
9
6
=
3
2
2
3
8
7
-
=
8
1
8
6
=
4
3
3
4
(教材第36页“第10题” )
6
5
+
=
6
5
6
10
=
3
5
5
3
12
11
-
=
12
7
12
4
=
3
1
1
3
7.
18
13
-
=
18
7
18
6
=
3
1
1
3
4
3
+
=
4
1
4
4
=
1
(教材第36页“第10题” )
10
3
+
=
10
9
10
12
=
5
6
6
5
25
17
-
=
25
7
25
10
=
5
2
2
5
7.
8. 一个长方形花圃(如图),其中 种月季, 种菊花,
种一串红, 种玫瑰。
8
1
8
3
月
季
菊
花
玫
瑰
8
3
把这块地看作“1”
8
3
8
1
一
串
红
8
1
(1)种菊花和玫瑰的面积一共占花圃的几分之几?
(教材第36页“第11题” )
+ = =
答:种菊花和玫瑰的面积一共占花圃的 。
8
3
8
1
8
4
2
1
2
1
8. 一个长方形花圃(如图),其中 种月季, 种菊花,
种一串红, 种玫瑰。
8
1
8
3
月
季
菊
花
玫
瑰
8
3
把这块地看作“1”
8
3
8
1
一
串
红
8
1
(2)你还能提出什么问题?
- = =
8
3
8
1
8
2
4
1
(教材第36页“第11题” )
答案不唯一。如菊花比月季多占花圃的几分之几?
9. 化简一个分数时,用2约了两次,用3约了一次,得
。原来的分数时多少?
本题可用倒推法求解。
8
3
思路引导
( )÷2÷2÷3
( )÷2÷2÷3
=
8
3
÷2
÷2
÷2
÷2
÷3
÷3
×3
×3
×2
×2
×2
×2
8
3
24
9
=
48
18
96
36
=
×3
×3
=
×2
×2
×2
×2
9. 化简一个分数时,用2约了两次,用3约了一次,得
。原来的分数时多少?
8
3
规范解答
3×3×2×2
8×3×2×2
=
96
36
答:原来的分数时 。
96
36
10. 一个最简分数,若将它的分子加上2,则等于 。这个分数可能是多少?
(教材第37页“第14题” )
2
1
思路引导
是经过化简得到的,可以先将分子分母分别乘2、3、4、5……再倒推进行判断。
2
1
2
1
4
2
×2
×2
=
-2
=
4
0
不符合
2
1
6
3
×3
×3
=
-2
=
6
1
符合 ……
规范解答
这个分数可能是 、 ……
6
1
10
3
11. 有红、黄、蓝三条丝带。红丝带比黄丝带长 m,蓝丝带比黄丝带短 m,红丝带与蓝丝带相差多少米?
20
7
20
3
方法 图解法
红丝带
黄丝带
蓝丝带
20
7
m
20
3
m
?
m
20
7
=
+
20
3
20
10
1
2
=
2
1
(米)
答:红丝带与蓝丝带相差 米。
2
1
约分:可以用分数的分子和分母同时除以它们的公因数,一直除到最简分数为止。
这节课你有什么收获
课堂小结
或用用分数的分子和分母同时除以它们的最大公因数,得到最简分数。
同分母分数相加减的计算方法:分母不变,分子相加减。计算结果能约分的,一般要约成最简分数。
这节课你有什么收获
完成相关练习。
02
01
课后练习题。
课后作业
同分母分数加减法
青岛版数学五年级(下)
三 剪纸中的数学
——分数的加减法(一)
1.理解分数加减法的意义,初步掌握同分母分数加减法的算理和计算法则。
2.结合情景了解约分的意义,掌握约分的方法。
3.使学生在新知的探索中,体验学习和探索的乐趣,培养学生学好数学的信心及团队协作能力。
学习目标
【重点】
同分母分数加减法的算理和计算法则。
【难点】
约分的方法。
你能提出哪些数学问题?
课堂导入
我吃了 。
1
9
我吃了 。
4
9
蝴 蝶
鲤鱼
1
8
3
8
你还能提出什么问题?
从图中,你能知道哪些数学信息?
剪鲤鱼和蝴蝶一共用了这张纸的几分之几
剪鲤鱼比蝴蝶少用了这张纸的几分之几
我剪鲤鱼用这张纸的 。
1
8
我剪蝴蝶用了这张纸的 。
3
8
新知探究
剪鲤鱼和蝴蝶一共用了这张纸的几分之几
鲤 鱼
蝴 蝶
1
8
3
8
?
1个 加3个 是
4个 ,就是 ,
所以 + = 。
1
8
1
8
4
8
1
8
3
8
1
8
4
8
根据分数的基本性质可以把得数化成更简单的分数:
1
2
÷
=
=
4
8
8
4
÷
4
4
+ =
=
1
8
3
8
1+3
8
4
8
答:剪鲤鱼和蝴蝶一共用了这张纸的 。
1
2
1
2
=
剪鲤鱼和蝴蝶一共用了这张纸的几分之几
把一个分数化成同它相等,但分子、分母都
比较小的分数,叫作约分。
8
1
=
+
8
3
8
1+3
8
4
=
1
2
=
2
1
分母不变
分子相加
不是最简分数
约成最简分数
分数加法的意义和整数加法的意义相同,都是把两个数合并成一个数的运算。
你会把 约分吗?
12
18
9
6
2
18
2
12
18
12
÷
÷
=
=
分别除以分子和分母的公因数2。
9
6
2
18
2
12
18
12
÷
÷
=
=
3
2
3
9
3
6
9
6
÷
÷
=
=
分子和分母先
分别除以公因数2,再除以公因数3。
小丽
小红
你会把 约分吗?
12
18
分子和分母可以直接除以分子和分母的最大公因数6。
3
2
6
18
6
12
18
12
÷
÷
=
=
小刚
他们约分的结果为什么不同呢?
9
6
2
18
2
12
18
12
÷
÷
=
=
3
2
6
18
6
12
18
12
÷
÷
=
=
小刚
小丽
小丽约分的结果
还可以再约分
……
9
6
有公因数3
的分子和分母只有公因数1,像这样的分数叫作最简分数。约分时通常要约成最简分数。
3
2
约分可以写成下面的形式。
18
12
=
18
12
6
9
2
3
3
2
=
18
12
=
18
12
2
3
3
2
=
先分别除以18和12的公因数2。
再分别除以6和9的公因数3。
也可以分别除以18和12的最大公因数6。
或直接写成
18
12
=
3
2
逐步约分法
一次约分法
剪蝴蝶比剪鲤鱼多用了这张纸的几分之几?
鲤 鱼
蝴 蝶
1
8
3
8
?
3个 减1个 是
2个 ,就是 ,
所以 - = 。
1
8
1
8
2
8
1
8
1
8
3
8
2
8
剪蝴蝶比剪鲤鱼多用了这张纸的几分之几?
剪蝴蝶比剪鲤鱼多用了这张纸的几分之几?
8
3
-
=
8
1
8
2
=
4
1
1
4
计算结果能约分,一般要约成最简分数。
答:剪蝴蝶比剪鲤鱼多用了这张纸的 。
4
1
剪蝴蝶比剪鲤鱼多用了这张纸的几分之几?
8
3-1
=
8
3
=
-
8
1
8
3-1
8
2
=
1
4
=
4
1
分母不变
分子相减
不是最简分数
约成最简分数
分数减法的意义和整数减法的意义相同,都是已知两个数的和与其中一个加数,求另一个加数的运算。
共同点
8
1
=
+
8
3
8
1+3
8
4
=
1
2
=
2
1
8
3
=
-
8
1
8
3-1
8
2
=
1
4
=
4
1
观察两个算式,你能发现什么共同点吗?
分母相同
①都是分母相同的分数相加、减;
分子相加减
分母不变
②计算时,只把分子相加减,分母不变;
最简分数
③计算结果都是最简分数。
请你概括同分母分数加减法的计算法则。
同分母分数相加、减,分母不变。
只把分子相加、减。
同分母分数加减法的计算法则:分母不变,只把分子相加、减。计算结果能约分的要约成最简分数。
1.填空。
课堂练习
(教材第35页“第1题” )
5
4
30
24
30
24
÷
÷
=
=
6
6
4
3
28
21
28
21
÷
÷
=
=
7
7
9
7
45
72
=
=
35
56
4
12
36
9
=
=
3
1
×5
÷3
×8
÷9
2. 把上下相等的数连一连。
7
3
6
4
5
2
8
6
9
3
21
9
4
3
3
1
25
10
3
2
(教材第35页“第5题” )
21
6
7
4
10
8
5
3
4
1
28
7
12
7
36
3
18
12
5
2
4
3
15
9
2
7
<
4
5
<
1
4
=
1
12
>
2
3
>
3
5
>
3.先化简,再比较下面每组中两个分数的大小。
(2)分数 的分子和分母的最大公因数是( ) ,化成最简分数是( )。
(1)一个分数约分后,分数的大小( )。
4. 填一填。
(3)分母是 8 的最简真分数的和是( )。
不变
3
2
(4)一个最简真分数,分子和分母的积是7,这个分数是( )。
27
6
9
2
7
1
(教材第36页“第6题” )
5. 2012年伦敦奥运会的跳水项目设有8枚金牌,被誉为“梦之队”的中国跳水队夺得了6枚。中国跳水队夺得的金牌数占跳水项目金牌总数的几分之几?
=
6÷8
4
3
答:中国跳水队夺得的金牌数占
跳水项目金牌总数的 。
4
3
6. 在括号里填上最简分数。
40分=( )时
75cm=( )m
20秒=( )分
500千克=( )吨
=( )
35dm=( )m
40÷60=
40
60
2
3
=
3
2
75÷100=
75
100
3
4
=
4
3
20÷60=
20
60
1
3
=
3
1
35÷10=
35
10
7
2
=
2
7
500÷1000=
500
1000
1
2
=
2
1
60÷100=
60
100
3
5
=
5
3
9
2
+
=
9
4
9
6
=
3
2
2
3
8
7
-
=
8
1
8
6
=
4
3
3
4
(教材第36页“第10题” )
6
5
+
=
6
5
6
10
=
3
5
5
3
12
11
-
=
12
7
12
4
=
3
1
1
3
7.
18
13
-
=
18
7
18
6
=
3
1
1
3
4
3
+
=
4
1
4
4
=
1
(教材第36页“第10题” )
10
3
+
=
10
9
10
12
=
5
6
6
5
25
17
-
=
25
7
25
10
=
5
2
2
5
7.
8. 一个长方形花圃(如图),其中 种月季, 种菊花,
种一串红, 种玫瑰。
8
1
8
3
月
季
菊
花
玫
瑰
8
3
把这块地看作“1”
8
3
8
1
一
串
红
8
1
(1)种菊花和玫瑰的面积一共占花圃的几分之几?
(教材第36页“第11题” )
+ = =
答:种菊花和玫瑰的面积一共占花圃的 。
8
3
8
1
8
4
2
1
2
1
8. 一个长方形花圃(如图),其中 种月季, 种菊花,
种一串红, 种玫瑰。
8
1
8
3
月
季
菊
花
玫
瑰
8
3
把这块地看作“1”
8
3
8
1
一
串
红
8
1
(2)你还能提出什么问题?
- = =
8
3
8
1
8
2
4
1
(教材第36页“第11题” )
答案不唯一。如菊花比月季多占花圃的几分之几?
9. 化简一个分数时,用2约了两次,用3约了一次,得
。原来的分数时多少?
本题可用倒推法求解。
8
3
思路引导
( )÷2÷2÷3
( )÷2÷2÷3
=
8
3
÷2
÷2
÷2
÷2
÷3
÷3
×3
×3
×2
×2
×2
×2
8
3
24
9
=
48
18
96
36
=
×3
×3
=
×2
×2
×2
×2
9. 化简一个分数时,用2约了两次,用3约了一次,得
。原来的分数时多少?
8
3
规范解答
3×3×2×2
8×3×2×2
=
96
36
答:原来的分数时 。
96
36
10. 一个最简分数,若将它的分子加上2,则等于 。这个分数可能是多少?
(教材第37页“第14题” )
2
1
思路引导
是经过化简得到的,可以先将分子分母分别乘2、3、4、5……再倒推进行判断。
2
1
2
1
4
2
×2
×2
=
-2
=
4
0
不符合
2
1
6
3
×3
×3
=
-2
=
6
1
符合 ……
规范解答
这个分数可能是 、 ……
6
1
10
3
11. 有红、黄、蓝三条丝带。红丝带比黄丝带长 m,蓝丝带比黄丝带短 m,红丝带与蓝丝带相差多少米?
20
7
20
3
方法 图解法
红丝带
黄丝带
蓝丝带
20
7
m
20
3
m
?
m
20
7
=
+
20
3
20
10
1
2
=
2
1
(米)
答:红丝带与蓝丝带相差 米。
2
1
约分:可以用分数的分子和分母同时除以它们的公因数,一直除到最简分数为止。
这节课你有什么收获
课堂小结
或用用分数的分子和分母同时除以它们的最大公因数,得到最简分数。
同分母分数相加减的计算方法:分母不变,分子相加减。计算结果能约分的,一般要约成最简分数。
这节课你有什么收获
完成相关练习。
02
01
课后练习题。
课后作业
