青岛版五年级数学下册三 剪纸中的数学-分数加减法(一)回顾整理 课件(共31张PPT)
文档属性
| 名称 | 青岛版五年级数学下册三 剪纸中的数学-分数加减法(一)回顾整理 课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 12:37:30 | ||
图片预览








文档简介
(共31张PPT)
回顾整理
青岛版数学五年级(下)
三 剪纸中的数学
——分数加减法(一)
我学会了同分母分数加减法和连加、连减的计算方法。
通过前面的学习,你们学会了什么?
我学会了找最大公因数和最小公倍数。
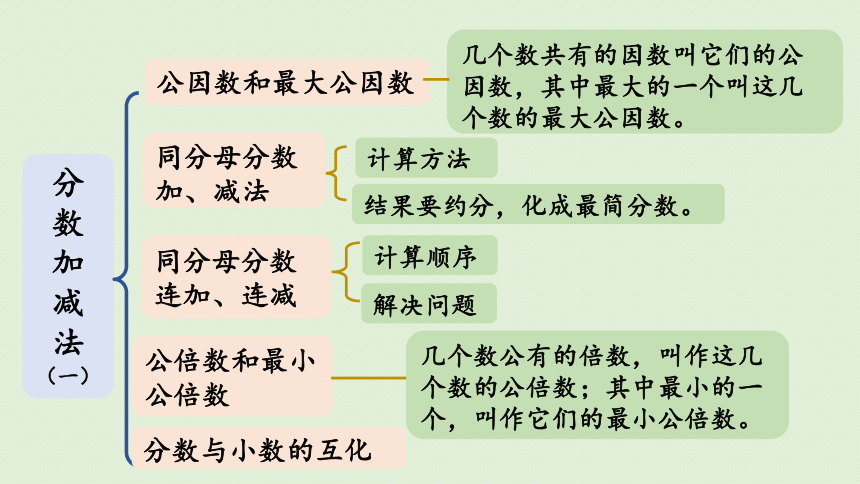
知识梳理
分
数
加
减
法
(一)
公因数和最大公因数
公倍数和最小公倍数
计算方法
几个数共有的因数叫它们的公因数,其中最大的一个叫这几个数的最大公因数。
结果要约分,化成最简分数。
同分母分数加、减法
同分母分数连加、连减
计算顺序
解决问题
几个数公有的倍数,叫作这几个数的公倍数;其中最小的一个,叫作它们的最小公倍数。
分数与小数的互化
要点回顾
要点1:公因数和最大公因数
1.填一填。
18的因数有
30的因数有
18和30的公因数有
最大公因数是
1、2、3、6、9、18
1、2、3、5、6、10、15、30
1、2、3、6
公因数中最大的那个
6
2.把长72cm、宽54cm的铁板裁成若干个面积相等的小正方形而没有剩余,裁出的小正方形的边长最大是多少厘米?
找长和宽的公因数
最大公因数
2
27
3
3
3
4
12
9
72
54
36
72和54的最大公因数是
2×3×3=18
答:裁出的小正方形的边长最大是18厘米。
公因数
最大公因数
公因数和最大公因数
的关系:
要点2:同分母分数加减法及约分
3.约分是根据( ),把分数的分子和分母同时( )化成同它相等,但分子、分母都( )的分数。
分数的基本性质
除以它们的最大公因数
比较小的
4.把下面的分数化成最简分数。
28
84
28
=
84÷( )
28÷( )
=
3
( )
28
1
84
28
=
42
( )
=
( )
( )
1
14
3
约分的方法:
①用分数的分子和分母同时除以它们的公因数,一直除到最简分数为止。
②也可以用分子和分母的最大公因数直接去除,即可得到最简分数。
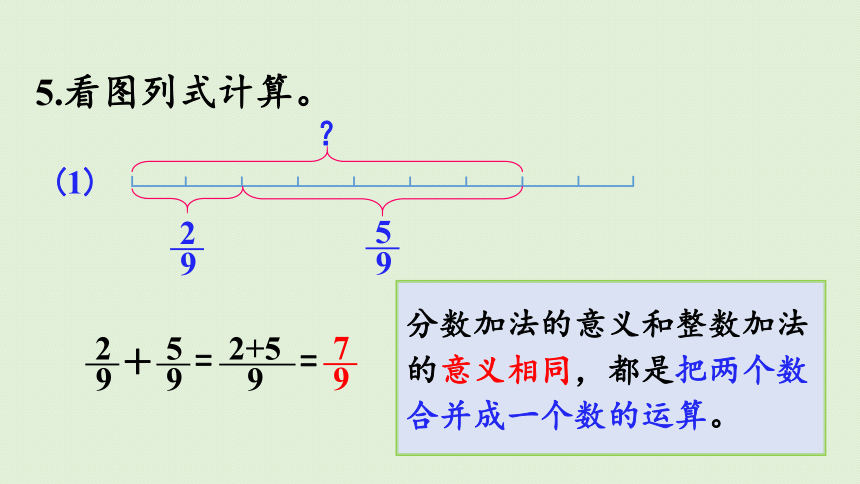
5.看图列式计算。
?
9
2
9
5
(1)
9
2
=
+
9
5
9
2+5
=
9
7
分数加法的意义和整数加法的意义相同,都是把两个数合并成一个数的运算。
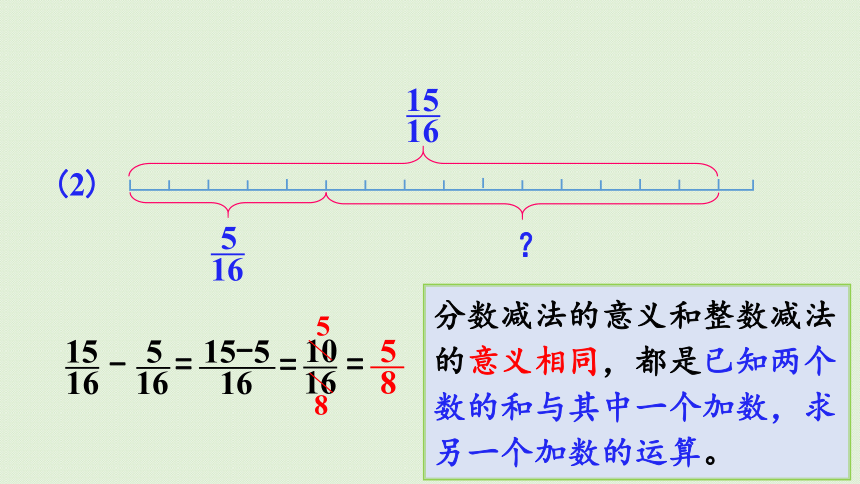
?
16
5
16
15
(2)
16
15
=
-
16
5
16
15-5
=
16
10
5
8
=
8
5
分数减法的意义和整数减法的意义相同,都是已知两个数的和与其中一个加数,求另一个加数的运算。
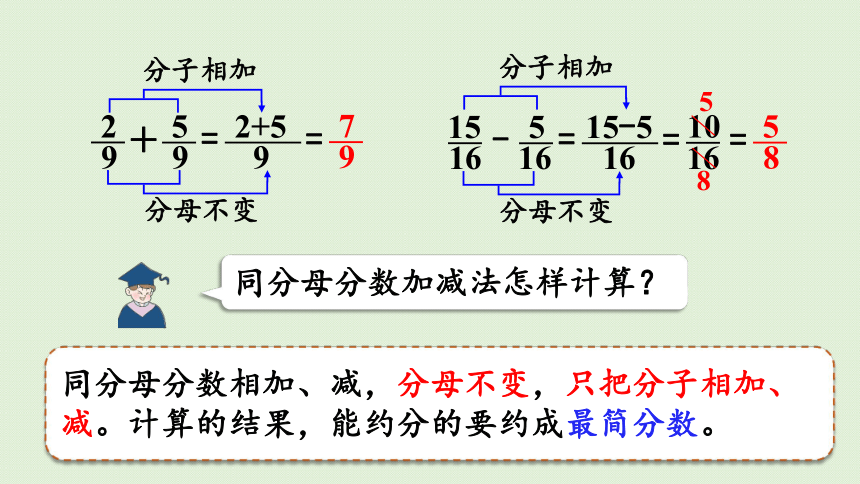
同分母分数加减法怎样计算?
9
2
=
+
9
5
9
2+5
=
9
7
16
15
=
-
16
5
16
15-5
=
16
10
5
8
=
8
5
分母不变
分子相加
分母不变
分子相加
同分母分数相加、减,分母不变,只把分子相加、减。计算的结果,能约分的要约成最简分数。
要点3:同分母分数连加、连减
6. 某精面加工厂三天刚好加工1吨面粉。第一天加工 吨,第二天加工 吨,第三天加工多少吨?
1吨面粉
第三天
第一天+第二天+第三天=1吨
25
7
25
8
25
7
25
8
6. 某精面加工厂三天刚好加工1吨面粉。第一天加工 吨,第二天加工 吨,第三天加工多少吨?
25
7
25
8
1- - =
25
7
25
8
(吨)
5
2
答:第三天加工 吨。
5
2
7.
9
2
9
4
+
9
2
+
9
1
+
9
5
-
9
6
9
8
1
9
4
11
5
11
3
+
11
5
+
11
4
-
11
8
-
11
8
11
13
11
9
11
1
同分母分数同分母分数连加、连减,既可以按从左到右的顺序依次进行计算,也可以将分子连续相加、相减,分母不变。最后结果不是最简分数的,要约分成最简分数。
要点4:公倍数和最小公倍数
9.若非零自然数a和b只有公因数1,则它们的最大公因数是( ),最小公倍数是( )。
8. 24和36的最大公因数是( ),最小公倍数是( )。
14
72
1
a×b
列举法 筛选法 短除法
10.暑假期间,小亮和小明都去参加游泳训练。小亮8天去一次,小明6天去一次。7月31日两人同时参加训练后,几月几日他们再次同时参加训练?
8和6的最小公倍数是24。
答:8月24日他们再次同时参加训练。
要点5 分数和小数的互化
11.填一填。
(1)0.6里面有( )个( )分之一,表示
( )分之( ),化成分数是( )。
(2)0.36里面有( )个( )分之一,表示
( )分之( ),化成分数是( )。
6
十
十
六
36
百
百
三十六
5
3
25
9
12. 把 、0.75、 、 、 按从小到大的顺序排列起来。
100
57
8
5
10
7
10
7
= 0.7
100
57
= 0.57
7
5
= 5÷7 ≈ 0.714
= 5÷8 = 0.625
8
5
因为 0.57<0.625<0.7<0.714<0.75
7
5
所以
<
<
10
7
100
57
<
<
0.75
8
5
7
5
分数化成小数,要用分子除以分母,除不尽时,可以根据需要按“四舍五入”法保留几位小数。
小数化成分数,原来有几位小数,就在1的后面写几个零作分母,把原来的小数点去掉作分子。能约分的要约分。
1. 计算下面各题,结果保留最简分数或整数。
课堂练习
9
1
-
=
9
4
9
4
1-
27
5
-
=
27
8
+
27
25
27
22
15
7
+
=
15
4
-
15
13
1
12
4
+
=
12
7
+
12
1
3
2
0.6 0.12 0.45 2.75 0.9 1.025
2. 把下面每个小数和同它相等的分数用线连起来。
10
9
5
3
40
1
1
25
3
20
9
4
3
2
3.解决问题。
(1)乐乐看一本连环画,第一天看了这本书的
,第二天看了这本书的 ,两天一共
看了这本书的几分之几?第二天比第一天
多看了这本书的几分之几?
9
2
9
4
答:两天一共看了这本书的 。
3
2
9
2
9
4
+
=
9
6
=
3
2
3.解决问题。
(1)乐乐看一本连环画,第一天看了这本书的
,第二天看了这本书的 ,两天一共
看了这本书的几分之几?第二天比第一天
多看了这本书的几分之几?
9
2
9
4
答:第二天比第一天多看了这本书的 。
9
2
9
4
9
2
-
=
9
2
3.解决问题。
(2)有两根钢管,一根长42分米,另一根长63
分米。现在要把它们锯成同样长的小段,
且没有剩余,每段钢管最长是多少分米?
一共能锯成多少段?
42与63的最大公因数是21。
42÷21=2(段) 62÷21=3(段)3+2=5(段)
答:每段钢管最长是21分米。一共能锯成5段。
就是求6和9在40以内的公倍数。
思路引导
先找出6和9 的公倍数,再与40人作比较。
(3)
如果这些学生的总人数在40人以内,可能是多少人?
咱们可以分成6人一组,也可以分成9人一组,都正好分完。
总人数必须是6和9的公倍数。
规范解答
(3)
6和9的公倍数有9, 18, 27, 36, 45, 54,…。
18<40, 36<40, 54>40, …
答:可能是18人或36人。
(4)为了迎接市运会,要在迎宾大道的一边等距离安装路灯,而且要在A、B、C三个点上各安装一盏路灯,如图所示,请你设计一个最省钱的方案。
思路引导
要设计等距离安装路灯最省钱的方案
相邻两盏路灯之间的距离应最大
720和640的最大公因数,即两盏灯间的最大距离
运用两端都栽的植树问题:盏数=路长÷间距+1
求出一共需要安装的总盏数
A
B
C
720m
640m
(4)为了迎接市运会,要在迎宾大道的一边等距离安装路灯,而且要在A、B、C三个点上各安装一盏路灯,如图所示,请你设计一个最省钱的方案。
规范解答
A
B
C
720m
640m
720
640
10
8
72
64
9
8
720和640的最大公因数是10×8=80。
(720+640)÷80+1=18(盏)
答:每隔80米安装一盏路灯,共安装18盏路灯最省钱。
用两个数的公因数去除更简便一些
(5)春游时,城北小学五年级的老师带同学们去划船。每3人一条船少1人,每5人一条船多2人,每7人一条船少5人。参加划船的至少有多少人?
思路引导
每3人一条船少1人
每3人一条船多2人
每7人一条船少5人
每7人一条船多2人
每5人一条船多2人
要求参加划船的至少有多少人,就是求比3, 5和7的最小公倍数还多2的数
(5)春游时,城北小学五年级的老师带同学们去划船。每3人一条船少1人,每5人一条船多2人,每7人一条船少5人。参加划船的至少有多少人?
规范解答
3, 5和7的最小公倍数是3×5×7=105。
105+2=107(人)
答:参加划船的至少有107人。
课后作业
完成相关练习。
02
01
课后练习。
回顾整理
青岛版数学五年级(下)
三 剪纸中的数学
——分数加减法(一)
我学会了同分母分数加减法和连加、连减的计算方法。
通过前面的学习,你们学会了什么?
我学会了找最大公因数和最小公倍数。
知识梳理
分
数
加
减
法
(一)
公因数和最大公因数
公倍数和最小公倍数
计算方法
几个数共有的因数叫它们的公因数,其中最大的一个叫这几个数的最大公因数。
结果要约分,化成最简分数。
同分母分数加、减法
同分母分数连加、连减
计算顺序
解决问题
几个数公有的倍数,叫作这几个数的公倍数;其中最小的一个,叫作它们的最小公倍数。
分数与小数的互化
要点回顾
要点1:公因数和最大公因数
1.填一填。
18的因数有
30的因数有
18和30的公因数有
最大公因数是
1、2、3、6、9、18
1、2、3、5、6、10、15、30
1、2、3、6
公因数中最大的那个
6
2.把长72cm、宽54cm的铁板裁成若干个面积相等的小正方形而没有剩余,裁出的小正方形的边长最大是多少厘米?
找长和宽的公因数
最大公因数
2
27
3
3
3
4
12
9
72
54
36
72和54的最大公因数是
2×3×3=18
答:裁出的小正方形的边长最大是18厘米。
公因数
最大公因数
公因数和最大公因数
的关系:
要点2:同分母分数加减法及约分
3.约分是根据( ),把分数的分子和分母同时( )化成同它相等,但分子、分母都( )的分数。
分数的基本性质
除以它们的最大公因数
比较小的
4.把下面的分数化成最简分数。
28
84
28
=
84÷( )
28÷( )
=
3
( )
28
1
84
28
=
42
( )
=
( )
( )
1
14
3
约分的方法:
①用分数的分子和分母同时除以它们的公因数,一直除到最简分数为止。
②也可以用分子和分母的最大公因数直接去除,即可得到最简分数。
5.看图列式计算。
?
9
2
9
5
(1)
9
2
=
+
9
5
9
2+5
=
9
7
分数加法的意义和整数加法的意义相同,都是把两个数合并成一个数的运算。
?
16
5
16
15
(2)
16
15
=
-
16
5
16
15-5
=
16
10
5
8
=
8
5
分数减法的意义和整数减法的意义相同,都是已知两个数的和与其中一个加数,求另一个加数的运算。
同分母分数加减法怎样计算?
9
2
=
+
9
5
9
2+5
=
9
7
16
15
=
-
16
5
16
15-5
=
16
10
5
8
=
8
5
分母不变
分子相加
分母不变
分子相加
同分母分数相加、减,分母不变,只把分子相加、减。计算的结果,能约分的要约成最简分数。
要点3:同分母分数连加、连减
6. 某精面加工厂三天刚好加工1吨面粉。第一天加工 吨,第二天加工 吨,第三天加工多少吨?
1吨面粉
第三天
第一天+第二天+第三天=1吨
25
7
25
8
25
7
25
8
6. 某精面加工厂三天刚好加工1吨面粉。第一天加工 吨,第二天加工 吨,第三天加工多少吨?
25
7
25
8
1- - =
25
7
25
8
(吨)
5
2
答:第三天加工 吨。
5
2
7.
9
2
9
4
+
9
2
+
9
1
+
9
5
-
9
6
9
8
1
9
4
11
5
11
3
+
11
5
+
11
4
-
11
8
-
11
8
11
13
11
9
11
1
同分母分数同分母分数连加、连减,既可以按从左到右的顺序依次进行计算,也可以将分子连续相加、相减,分母不变。最后结果不是最简分数的,要约分成最简分数。
要点4:公倍数和最小公倍数
9.若非零自然数a和b只有公因数1,则它们的最大公因数是( ),最小公倍数是( )。
8. 24和36的最大公因数是( ),最小公倍数是( )。
14
72
1
a×b
列举法 筛选法 短除法
10.暑假期间,小亮和小明都去参加游泳训练。小亮8天去一次,小明6天去一次。7月31日两人同时参加训练后,几月几日他们再次同时参加训练?
8和6的最小公倍数是24。
答:8月24日他们再次同时参加训练。
要点5 分数和小数的互化
11.填一填。
(1)0.6里面有( )个( )分之一,表示
( )分之( ),化成分数是( )。
(2)0.36里面有( )个( )分之一,表示
( )分之( ),化成分数是( )。
6
十
十
六
36
百
百
三十六
5
3
25
9
12. 把 、0.75、 、 、 按从小到大的顺序排列起来。
100
57
8
5
10
7
10
7
= 0.7
100
57
= 0.57
7
5
= 5÷7 ≈ 0.714
= 5÷8 = 0.625
8
5
因为 0.57<0.625<0.7<0.714<0.75
7
5
所以
<
<
10
7
100
57
<
<
0.75
8
5
7
5
分数化成小数,要用分子除以分母,除不尽时,可以根据需要按“四舍五入”法保留几位小数。
小数化成分数,原来有几位小数,就在1的后面写几个零作分母,把原来的小数点去掉作分子。能约分的要约分。
1. 计算下面各题,结果保留最简分数或整数。
课堂练习
9
1
-
=
9
4
9
4
1-
27
5
-
=
27
8
+
27
25
27
22
15
7
+
=
15
4
-
15
13
1
12
4
+
=
12
7
+
12
1
3
2
0.6 0.12 0.45 2.75 0.9 1.025
2. 把下面每个小数和同它相等的分数用线连起来。
10
9
5
3
40
1
1
25
3
20
9
4
3
2
3.解决问题。
(1)乐乐看一本连环画,第一天看了这本书的
,第二天看了这本书的 ,两天一共
看了这本书的几分之几?第二天比第一天
多看了这本书的几分之几?
9
2
9
4
答:两天一共看了这本书的 。
3
2
9
2
9
4
+
=
9
6
=
3
2
3.解决问题。
(1)乐乐看一本连环画,第一天看了这本书的
,第二天看了这本书的 ,两天一共
看了这本书的几分之几?第二天比第一天
多看了这本书的几分之几?
9
2
9
4
答:第二天比第一天多看了这本书的 。
9
2
9
4
9
2
-
=
9
2
3.解决问题。
(2)有两根钢管,一根长42分米,另一根长63
分米。现在要把它们锯成同样长的小段,
且没有剩余,每段钢管最长是多少分米?
一共能锯成多少段?
42与63的最大公因数是21。
42÷21=2(段) 62÷21=3(段)3+2=5(段)
答:每段钢管最长是21分米。一共能锯成5段。
就是求6和9在40以内的公倍数。
思路引导
先找出6和9 的公倍数,再与40人作比较。
(3)
如果这些学生的总人数在40人以内,可能是多少人?
咱们可以分成6人一组,也可以分成9人一组,都正好分完。
总人数必须是6和9的公倍数。
规范解答
(3)
6和9的公倍数有9, 18, 27, 36, 45, 54,…。
18<40, 36<40, 54>40, …
答:可能是18人或36人。
(4)为了迎接市运会,要在迎宾大道的一边等距离安装路灯,而且要在A、B、C三个点上各安装一盏路灯,如图所示,请你设计一个最省钱的方案。
思路引导
要设计等距离安装路灯最省钱的方案
相邻两盏路灯之间的距离应最大
720和640的最大公因数,即两盏灯间的最大距离
运用两端都栽的植树问题:盏数=路长÷间距+1
求出一共需要安装的总盏数
A
B
C
720m
640m
(4)为了迎接市运会,要在迎宾大道的一边等距离安装路灯,而且要在A、B、C三个点上各安装一盏路灯,如图所示,请你设计一个最省钱的方案。
规范解答
A
B
C
720m
640m
720
640
10
8
72
64
9
8
720和640的最大公因数是10×8=80。
(720+640)÷80+1=18(盏)
答:每隔80米安装一盏路灯,共安装18盏路灯最省钱。
用两个数的公因数去除更简便一些
(5)春游时,城北小学五年级的老师带同学们去划船。每3人一条船少1人,每5人一条船多2人,每7人一条船少5人。参加划船的至少有多少人?
思路引导
每3人一条船少1人
每3人一条船多2人
每7人一条船少5人
每7人一条船多2人
每5人一条船多2人
要求参加划船的至少有多少人,就是求比3, 5和7的最小公倍数还多2的数
(5)春游时,城北小学五年级的老师带同学们去划船。每3人一条船少1人,每5人一条船多2人,每7人一条船少5人。参加划船的至少有多少人?
规范解答
3, 5和7的最小公倍数是3×5×7=105。
105+2=107(人)
答:参加划船的至少有107人。
课后作业
完成相关练习。
02
01
课后练习。
