青岛版七 包装盒-长方体和正方体信息窗4 长方体和正方体体积 课件(共44张PPT)
文档属性
| 名称 | 青岛版七 包装盒-长方体和正方体信息窗4 长方体和正方体体积 课件(共44张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 12:40:09 | ||
图片预览





文档简介
(共44张PPT)
长方体和正方体体积
青岛版数学五年级(下)
二 包装盒
——长方体和正方体
1.理解容积意义,掌握常用的容积单位以及它们之间的进率。
2.掌握容积和体积的联系与区别,知道容积单位和体积单位之间的关系。
3.感受1毫升的实际意义,和应用所学知识解决生活中的简单问题。
学习目标
【重点】
建立体积和容积单位概念,及体积和容积单位换算。
【难点】
建立体积和容积单位概念。
乘飞机的行李规定
手提行李的三边之和一般不得超过115cm。
90cm
65cm
50cm
40cm
55cm
10cm
机场行李托运一般不超过此规格。
你知道其他交通工具关于行李尺寸的规定吗?
课堂导入
从图中,你能知道哪些数学信息?
可乐箱的长、宽、高分别是7dm、3dm、2dm。
桃汁饮料盒的长、宽、高分别是10cm、7cm、20cm。
啤酒箱的长、宽、高分别是3dm、3dm、3dm。
根据这些信息,你能提出什么问题?
新知探究
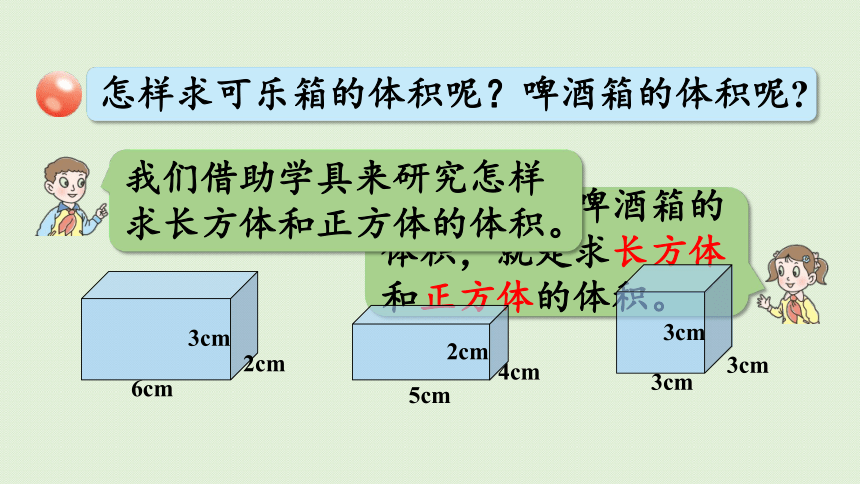
怎样求可乐箱的体积呢?啤酒箱的体积呢
求可乐箱和啤酒箱的体积,就是求长方体和正方体的体积。
我们借助学具来研究怎样求长方体和正方体的体积。
6cm
3cm
2cm
5cm
2cm
4cm
3cm
3cm
3cm
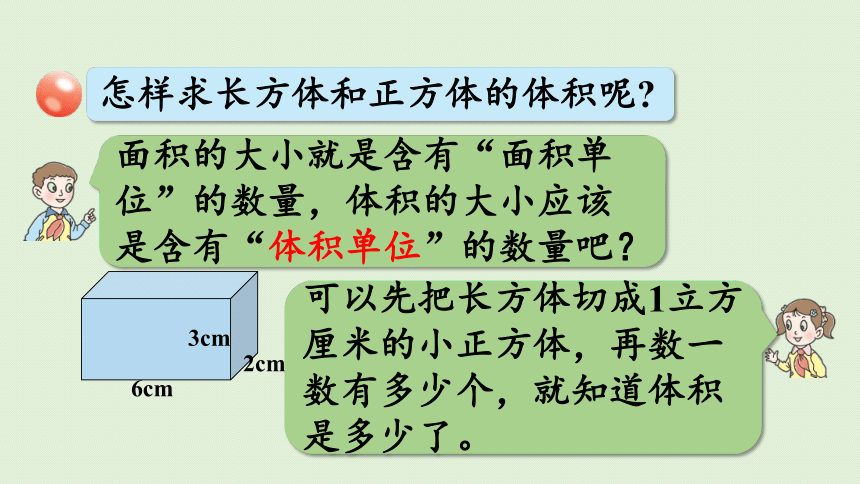
面积的大小就是含有“面积单位”的数量,体积的大小应该是含有“体积单位”的数量吧?
怎样求长方体和正方体的体积呢
6cm
3cm
2cm
可以先把长方体切成1立方厘米的小正方体,再数一数有多少个,就知道体积是多少了。
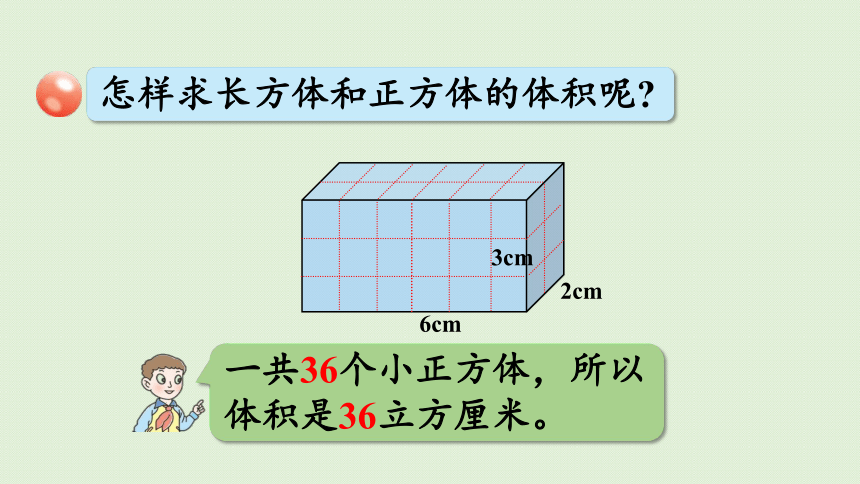
怎样求长方体和正方体的体积呢
6cm
3cm
2cm
一共36个小正方体,所以体积是36立方厘米。
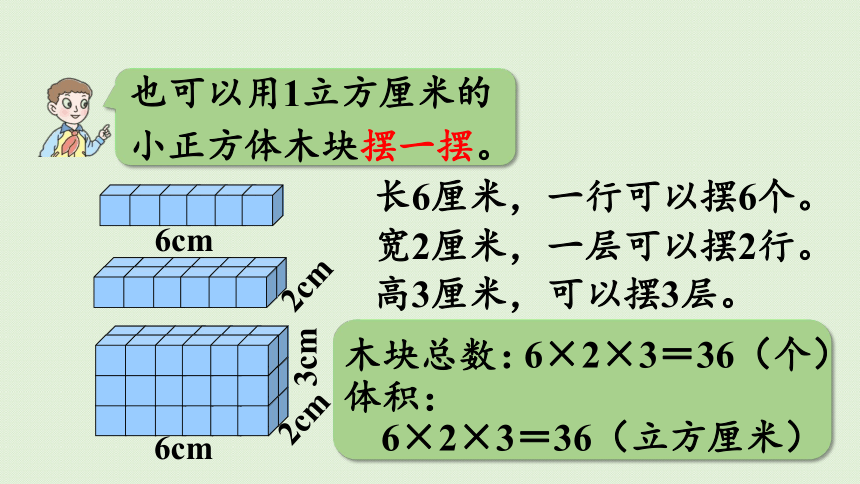
也可以用1立方厘米的小正方体木块摆一摆。
长6厘米,一行可以摆6个。
宽2厘米,一层可以摆2行。
2cm
6cm
高3厘米,可以摆3层。
3cm
6cm
2cm
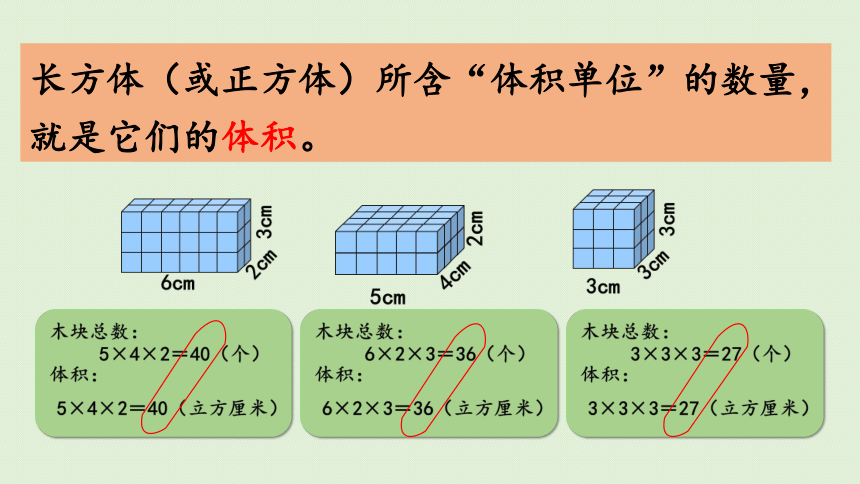
木块总数:
6×2×3=36(个)
体积:
6×2×3=36(立方厘米)
木块总数:
体积:
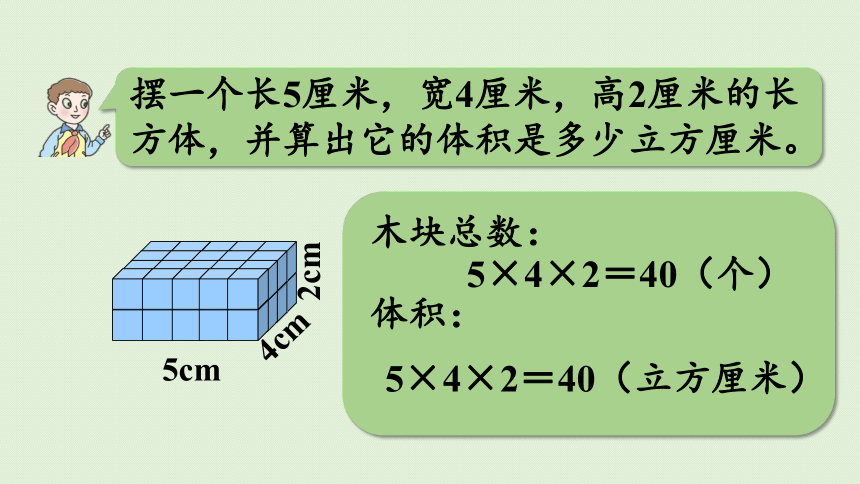
摆一个长5厘米,宽4厘米,高2厘米的长方体,并算出它的体积是多少立方厘米。
4cm
5cm
2cm
5×4×2=40(个)
5×4×2=40(立方厘米)
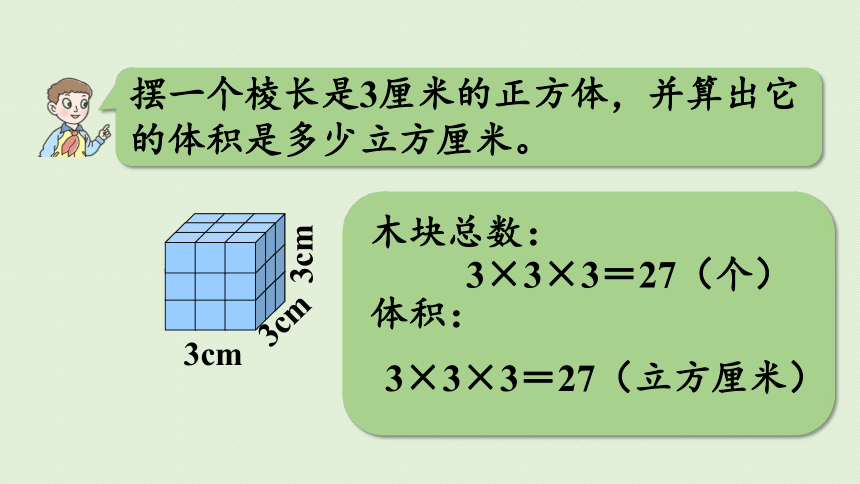
摆一个棱长是3厘米的正方体,并算出它的体积是多少立方厘米。
木块总数:
3×3×3=27(个)
体积:
3×3×3=27(立方厘米)
3cm
3cm
3cm
想一想,物体的体积与它所含“体积单位”的个数有着怎样的关系
长方体(或正方体)所含“体积单位”的数量,就是它们的体积。
长方体(或正方体)所含“体积单位”的数量,等于长、宽、高的乘积。
根据以上探索过程,如果V表示长方体、正方体的体积,用你能总结出长方体和正方体的体积计算公式吗?
ɑ
h
长方体的体积 = 长×宽×高
V=ɑbh
长
高
b
宽
正方体的体积 = 棱长×棱长×棱长
V=ɑ·ɑ·ɑ
ɑ·ɑ·ɑ也可以写作“ɑ3”,读作“ɑ的立方”,表示3个ɑ相乘。正方体的体积公式一般写成:
V=ɑ3
ɑ
ɑ
棱长
棱长
ɑ
棱长
正方体是特殊的长方体,长、宽、高都相等。
底面
底面
长方体或正方体底面的面积叫作底面积。
长方体底面积=
长×宽
正方体底面积=
棱长×棱长
想一想,长方体和正方体的体积还可以怎样计算?
底面
底面
想一想,长方体和正方体的体积还可以怎样计算?
长方体的体积=长×宽×高
底面积
长方体的体积=
×
高
底面
底面
想一想,长方体和正方体的体积还可以怎样计算?
正方体的体积=棱长×棱长×棱长
底面积
正方体的体积=
×
高
底面
底面
想一想,长方体和正方体的体积还可以怎样计算?
长方体(或正方体)的体积 = 底面积×高
V=sh
你会求可乐箱的体积吗?啤酒箱的体积呢
可乐箱的体积:
7×3×2 = 42(dm3)
啤酒箱的体积:
3×3×3 = 27(dm3)
答:可乐箱的体积是42 dm3 。
答:啤酒箱的体积是27 dm3 。
求桃汁饮料盒能盛多少升饮料,实际上就是求饮料盒的容积是多少。
厚度不计是什么意思?
桃汁饮料盒能盛多少升饮料?(盒壁厚度不计)
求桃汁饮料盒能盛多少升饮料,实际上就是求饮料盒的容积是多少。
厚度不计是什么意思?
桃汁饮料盒能盛多少升饮料?(盒壁厚度不计)
厚度忽略不计说明这时的饮料盒的容积和体积是一样的。
桃汁饮料盒能盛多少升饮料?(盒壁厚度不计)
10×7×20 = 1400(立方厘米)
1400立方厘米=1.4升
答:桃汁饮料盒能盛 1.4 升饮料。
长方体或正方体容器容积的计算方法与体积的计算方法相同,但要从容器里面量长、宽、高。
( ) cm3 ( ) cm3
课堂练习
1.你知道它们的体积各是多少吗?
(教材第98页“第1题” )
42
27
2.计算下面图形的体积。
(教材第98页“第2题” )
5×8×5=200(cm3)
4×4×4=64(dm3)
20×4×5=400(m3)
3.你知道下面这块明代长城砖的体积是多少立方厘米吗?(可用计算器计算)
(教材第98页“第3题” )
36.8×18.9×9.3=6468.336(cm3)
答:这块砖的体积是6468.336立方厘米。
4.右图是一瓶清洁剂。瓶的形状近似长方体,它长是7.3厘米,宽4厘米,高22厘米。这瓶清洁剂有多少毫升?(瓶壁厚度忽略不计)
(教材第98页“第4题” )
7.3×4×22 = 642.4(立方厘米)
642.4立方厘米 = 642.4毫升
答:这瓶清洁剂的容积是 642.4 毫升。
4 m3=
dm
1.4 dm =
cm3
850 dm3=
m3
45 cm =
dm3
2780 mL=
L
4000
1400
0.85
0.045
2.78
4×1000=4000
850÷1000=0.85
=
cm3
2.17
5.
(教材第98页“第5题” )
L
2170
6.右图中沙雕作品底座的形状是长方体,它的体积是96立方米,长和宽都是8米。这个沙雕底座的高是多少米?
(教材第98页“第6题” )
96÷(8×8)=1.5(米)
答:这个沙雕底座的高是1.5米。
7.一个泄洪坝共有20个泄洪孔,每个泄洪孔的宽是20米,高是125米。泄洪时,通过泄洪孔的水流速度是1.5/秒。每个泄洪孔每秒能泄洪多少立方米?
(教材第99页“第7题” )
1.5×20×125=3750(立方米)
答:每个泄洪孔每秒能泄洪3750立方米。
8.有一块长方体石料,长2.5米,宽1.6米,高1.2米。这块石料的体积是多少立方米?用一辆载重量是15吨的卡车运载这块石料,你觉得可以吗?(每立方米石料重2.7吨)
(教材第99页“第8题” )
2.5×1.6×1.2=4.8(立方米)
2.7×4.8=12.96(吨)
12.96<15,可以
9.有一个蓄水池(如下图),长10米,宽4米,深2米。
(教材第99页“第9题” )
10×4 = 40(平方米)
(1)蓄水池占地面积有多大?
答:占地面积是40平方米。
9.有一个蓄水池(如下图),长10米,宽4米,深2米。
(教材第99页“第9题” )
10×4 +(4×2+2×10)×2= 96(平方米)
(2)在蓄水池的底面和四周都抹上水泥,抹水泥的面积有多大?
答:抹水泥的面积有96平方米。
9.有一个蓄水池(如下图),长10米,宽4米,深2米。
(教材第99页“第9题” )
10×2 ×4= 80(立方米)
(3)蓄水池最多能蓄水多少立方米?
答:蓄水池最多能蓄水80立方米。
10.有一段长3米的方木,横截面是一个边长为0.2米的正方形。50根这样的方木的体积是多少立方米?
(教材第99页“第10题” )
0.12×50=6(立方米)
答:50根这样的方木,体积是6立方米。
0.2×0.2×3=0.12(立方米)
11.哈尔滨冰雪大世界每年用的冰大约能融化成8万立方米的水,它们相当于多少个长20m、宽20m、深2.5m的蓄水池的储水量?
(教材第99页“第11题” )
8万立方米=80000立方米
80000÷(20×20×2.5)=80(个)
答:相当于80个。
※12.
(教材第99页“第12题” )
生产左图所示的零件需要多少克钢材?(每立方厘米钢重7.8克)
15×6×(8-4)=360(立方厘米)
4×6×(15-5)=240(立方厘米)
(360+240)×7.8=4680(克)
13.辨一辨。
棱长是6m的正方体的表面积和体积相等。
( )
正方体的表面积=棱长×棱长×6
6×6×6=216(m )
正方体的体积=棱长×棱长×棱长
6×6×6=216(m )
表面积和体积是两个不同的概念,单位不一样,不能比较大小。
14.有一根长12dm的长方体木料,把它平均锯成3段(如图)表面积增加了100dm3,原来这根木料的体积是多少?
100÷2=50(dm3)
50×15=750(dm3)
15.将一块体积2dm3的长方体橡皮泥捏成正方体,它的体积是( )。
2dm3
立体图形变化,体积不变。
(1)8×10×22=1760(dm3)
16.计算下面图形的体积。
8dm
10dm
22dm
(2)
64dm2
20dm
(1)
(2)64×20=1280(cm3)
17.选一选。
(1)用棱长2厘米的小正方体拼成一个大正方体,大正方体的体积可能是( )立方厘米。
A.32 B.24 C.64 D.16
(2)一个长方体的长、宽、高分别扩大到原来的2倍,它的体积扩大到原来的( )倍。
A.6 B.8 C.9 D.27
C
B
长方体的体积=长×宽×高,
V=ɑbh;
正方体的体积=棱长×棱长×棱长
V=ɑ·ɑ·ɑ=ɑ3。
这节课你有什么收获
课堂小结
长方体(或正方体)的体积=底面积×高,V=Sh。
完成相关练习。
02
01
课后练习题。
课后作业
长方体和正方体体积
青岛版数学五年级(下)
二 包装盒
——长方体和正方体
1.理解容积意义,掌握常用的容积单位以及它们之间的进率。
2.掌握容积和体积的联系与区别,知道容积单位和体积单位之间的关系。
3.感受1毫升的实际意义,和应用所学知识解决生活中的简单问题。
学习目标
【重点】
建立体积和容积单位概念,及体积和容积单位换算。
【难点】
建立体积和容积单位概念。
乘飞机的行李规定
手提行李的三边之和一般不得超过115cm。
90cm
65cm
50cm
40cm
55cm
10cm
机场行李托运一般不超过此规格。
你知道其他交通工具关于行李尺寸的规定吗?
课堂导入
从图中,你能知道哪些数学信息?
可乐箱的长、宽、高分别是7dm、3dm、2dm。
桃汁饮料盒的长、宽、高分别是10cm、7cm、20cm。
啤酒箱的长、宽、高分别是3dm、3dm、3dm。
根据这些信息,你能提出什么问题?
新知探究
怎样求可乐箱的体积呢?啤酒箱的体积呢
求可乐箱和啤酒箱的体积,就是求长方体和正方体的体积。
我们借助学具来研究怎样求长方体和正方体的体积。
6cm
3cm
2cm
5cm
2cm
4cm
3cm
3cm
3cm
面积的大小就是含有“面积单位”的数量,体积的大小应该是含有“体积单位”的数量吧?
怎样求长方体和正方体的体积呢
6cm
3cm
2cm
可以先把长方体切成1立方厘米的小正方体,再数一数有多少个,就知道体积是多少了。
怎样求长方体和正方体的体积呢
6cm
3cm
2cm
一共36个小正方体,所以体积是36立方厘米。
也可以用1立方厘米的小正方体木块摆一摆。
长6厘米,一行可以摆6个。
宽2厘米,一层可以摆2行。
2cm
6cm
高3厘米,可以摆3层。
3cm
6cm
2cm
木块总数:
6×2×3=36(个)
体积:
6×2×3=36(立方厘米)
木块总数:
体积:
摆一个长5厘米,宽4厘米,高2厘米的长方体,并算出它的体积是多少立方厘米。
4cm
5cm
2cm
5×4×2=40(个)
5×4×2=40(立方厘米)
摆一个棱长是3厘米的正方体,并算出它的体积是多少立方厘米。
木块总数:
3×3×3=27(个)
体积:
3×3×3=27(立方厘米)
3cm
3cm
3cm
想一想,物体的体积与它所含“体积单位”的个数有着怎样的关系
长方体(或正方体)所含“体积单位”的数量,就是它们的体积。
长方体(或正方体)所含“体积单位”的数量,等于长、宽、高的乘积。
根据以上探索过程,如果V表示长方体、正方体的体积,用你能总结出长方体和正方体的体积计算公式吗?
ɑ
h
长方体的体积 = 长×宽×高
V=ɑbh
长
高
b
宽
正方体的体积 = 棱长×棱长×棱长
V=ɑ·ɑ·ɑ
ɑ·ɑ·ɑ也可以写作“ɑ3”,读作“ɑ的立方”,表示3个ɑ相乘。正方体的体积公式一般写成:
V=ɑ3
ɑ
ɑ
棱长
棱长
ɑ
棱长
正方体是特殊的长方体,长、宽、高都相等。
底面
底面
长方体或正方体底面的面积叫作底面积。
长方体底面积=
长×宽
正方体底面积=
棱长×棱长
想一想,长方体和正方体的体积还可以怎样计算?
底面
底面
想一想,长方体和正方体的体积还可以怎样计算?
长方体的体积=长×宽×高
底面积
长方体的体积=
×
高
底面
底面
想一想,长方体和正方体的体积还可以怎样计算?
正方体的体积=棱长×棱长×棱长
底面积
正方体的体积=
×
高
底面
底面
想一想,长方体和正方体的体积还可以怎样计算?
长方体(或正方体)的体积 = 底面积×高
V=sh
你会求可乐箱的体积吗?啤酒箱的体积呢
可乐箱的体积:
7×3×2 = 42(dm3)
啤酒箱的体积:
3×3×3 = 27(dm3)
答:可乐箱的体积是42 dm3 。
答:啤酒箱的体积是27 dm3 。
求桃汁饮料盒能盛多少升饮料,实际上就是求饮料盒的容积是多少。
厚度不计是什么意思?
桃汁饮料盒能盛多少升饮料?(盒壁厚度不计)
求桃汁饮料盒能盛多少升饮料,实际上就是求饮料盒的容积是多少。
厚度不计是什么意思?
桃汁饮料盒能盛多少升饮料?(盒壁厚度不计)
厚度忽略不计说明这时的饮料盒的容积和体积是一样的。
桃汁饮料盒能盛多少升饮料?(盒壁厚度不计)
10×7×20 = 1400(立方厘米)
1400立方厘米=1.4升
答:桃汁饮料盒能盛 1.4 升饮料。
长方体或正方体容器容积的计算方法与体积的计算方法相同,但要从容器里面量长、宽、高。
( ) cm3 ( ) cm3
课堂练习
1.你知道它们的体积各是多少吗?
(教材第98页“第1题” )
42
27
2.计算下面图形的体积。
(教材第98页“第2题” )
5×8×5=200(cm3)
4×4×4=64(dm3)
20×4×5=400(m3)
3.你知道下面这块明代长城砖的体积是多少立方厘米吗?(可用计算器计算)
(教材第98页“第3题” )
36.8×18.9×9.3=6468.336(cm3)
答:这块砖的体积是6468.336立方厘米。
4.右图是一瓶清洁剂。瓶的形状近似长方体,它长是7.3厘米,宽4厘米,高22厘米。这瓶清洁剂有多少毫升?(瓶壁厚度忽略不计)
(教材第98页“第4题” )
7.3×4×22 = 642.4(立方厘米)
642.4立方厘米 = 642.4毫升
答:这瓶清洁剂的容积是 642.4 毫升。
4 m3=
dm
1.4 dm =
cm3
850 dm3=
m3
45 cm =
dm3
2780 mL=
L
4000
1400
0.85
0.045
2.78
4×1000=4000
850÷1000=0.85
=
cm3
2.17
5.
(教材第98页“第5题” )
L
2170
6.右图中沙雕作品底座的形状是长方体,它的体积是96立方米,长和宽都是8米。这个沙雕底座的高是多少米?
(教材第98页“第6题” )
96÷(8×8)=1.5(米)
答:这个沙雕底座的高是1.5米。
7.一个泄洪坝共有20个泄洪孔,每个泄洪孔的宽是20米,高是125米。泄洪时,通过泄洪孔的水流速度是1.5/秒。每个泄洪孔每秒能泄洪多少立方米?
(教材第99页“第7题” )
1.5×20×125=3750(立方米)
答:每个泄洪孔每秒能泄洪3750立方米。
8.有一块长方体石料,长2.5米,宽1.6米,高1.2米。这块石料的体积是多少立方米?用一辆载重量是15吨的卡车运载这块石料,你觉得可以吗?(每立方米石料重2.7吨)
(教材第99页“第8题” )
2.5×1.6×1.2=4.8(立方米)
2.7×4.8=12.96(吨)
12.96<15,可以
9.有一个蓄水池(如下图),长10米,宽4米,深2米。
(教材第99页“第9题” )
10×4 = 40(平方米)
(1)蓄水池占地面积有多大?
答:占地面积是40平方米。
9.有一个蓄水池(如下图),长10米,宽4米,深2米。
(教材第99页“第9题” )
10×4 +(4×2+2×10)×2= 96(平方米)
(2)在蓄水池的底面和四周都抹上水泥,抹水泥的面积有多大?
答:抹水泥的面积有96平方米。
9.有一个蓄水池(如下图),长10米,宽4米,深2米。
(教材第99页“第9题” )
10×2 ×4= 80(立方米)
(3)蓄水池最多能蓄水多少立方米?
答:蓄水池最多能蓄水80立方米。
10.有一段长3米的方木,横截面是一个边长为0.2米的正方形。50根这样的方木的体积是多少立方米?
(教材第99页“第10题” )
0.12×50=6(立方米)
答:50根这样的方木,体积是6立方米。
0.2×0.2×3=0.12(立方米)
11.哈尔滨冰雪大世界每年用的冰大约能融化成8万立方米的水,它们相当于多少个长20m、宽20m、深2.5m的蓄水池的储水量?
(教材第99页“第11题” )
8万立方米=80000立方米
80000÷(20×20×2.5)=80(个)
答:相当于80个。
※12.
(教材第99页“第12题” )
生产左图所示的零件需要多少克钢材?(每立方厘米钢重7.8克)
15×6×(8-4)=360(立方厘米)
4×6×(15-5)=240(立方厘米)
(360+240)×7.8=4680(克)
13.辨一辨。
棱长是6m的正方体的表面积和体积相等。
( )
正方体的表面积=棱长×棱长×6
6×6×6=216(m )
正方体的体积=棱长×棱长×棱长
6×6×6=216(m )
表面积和体积是两个不同的概念,单位不一样,不能比较大小。
14.有一根长12dm的长方体木料,把它平均锯成3段(如图)表面积增加了100dm3,原来这根木料的体积是多少?
100÷2=50(dm3)
50×15=750(dm3)
15.将一块体积2dm3的长方体橡皮泥捏成正方体,它的体积是( )。
2dm3
立体图形变化,体积不变。
(1)8×10×22=1760(dm3)
16.计算下面图形的体积。
8dm
10dm
22dm
(2)
64dm2
20dm
(1)
(2)64×20=1280(cm3)
17.选一选。
(1)用棱长2厘米的小正方体拼成一个大正方体,大正方体的体积可能是( )立方厘米。
A.32 B.24 C.64 D.16
(2)一个长方体的长、宽、高分别扩大到原来的2倍,它的体积扩大到原来的( )倍。
A.6 B.8 C.9 D.27
C
B
长方体的体积=长×宽×高,
V=ɑbh;
正方体的体积=棱长×棱长×棱长
V=ɑ·ɑ·ɑ=ɑ3。
这节课你有什么收获
课堂小结
长方体(或正方体)的体积=底面积×高,V=Sh。
完成相关练习。
02
01
课后练习题。
课后作业
