第4课时 确定圆的条件 课时训练(含答案)
文档属性
| 名称 | 第4课时 确定圆的条件 课时训练(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 43.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-16 00:00:00 | ||
图片预览

文档简介
第4课时 确定圆的条件
【基础巩固】
1.经过一点作圆可以作_______个圆;经过两点作圆可以作_______个圆,这些圆的圆心在这两点的_______上;经过_______的三点可以作_______个圆,并且只能作_______个圆.
2.三角形的外心是三角形的_______的圆心,它是三角形的_______的交点,它到_______的距离相等.
3.已知△ABC中,∠A=80°,若点O是△ABC的外心,则∠BOC=_______.
4.下列命题正确的是 ( )
A.三点确定一个圆
B.三角形的外心是三角形三个角的平分线的交点
C.圆有且只有一个内接三角形
D.三角形的外心是三角形任意两边的垂直平分线的交点
5.已知AB=7 cm,则过点A、B,且半径为3 cm的圆有 ( )
A.0个 B.1个 C.2个 D.无数个
6.下列四边形中,一定有外接圆的是 ( )
A.平行四边形 B.菱形 C.矩形 D.梯形
7.在Rt△ABC中,∠C=90°,若AC=6,BC=8,求Rt△ABC的外接圆的半径和面积.
8.(1)作四边形ABCD,使∠A=∠C=90°;
(2)经过点A、B、D作⊙O,⊙O是否经过点C 请说明理由.
9.活动与探究:
如图,CD所在的直线垂直平分线段AB.怎样使用这样的工具找到圆形工件的圆心?
【拓展提优】
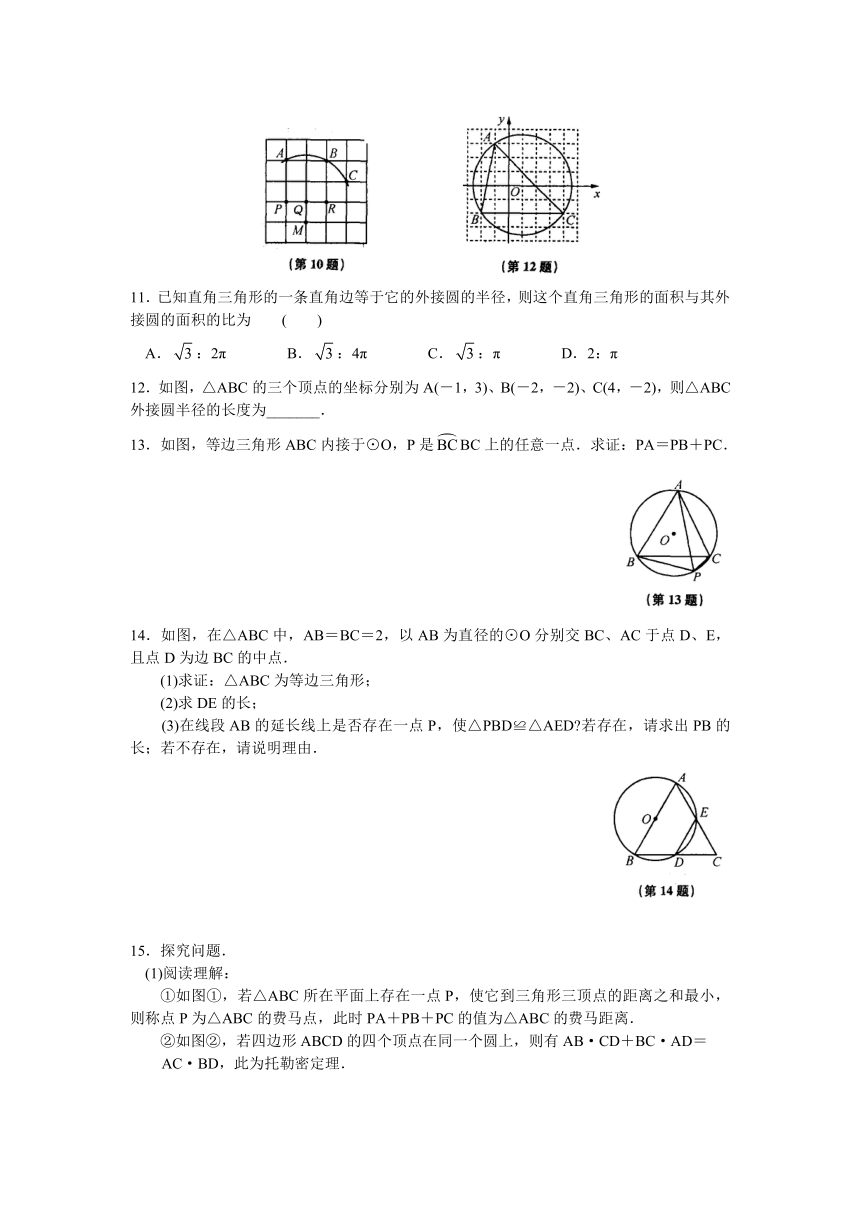
10.如图,在5×5正方形网格中,一条圆弧经过A、B、C三点,那么这条弧所在圆的圆心是( )
A.点P B.点Q C.点R D.点M
11.已知直角三角形的一条直角边等于它的外接圆的半径,则这个直角三角形的面积与其外接圆的面积的比为 ( )
A.:2π B.:4π C.:π D.2:π
12.如图,△ABC的三个顶点的坐标分别为A(-1,3)、B(-2,-2)、C(4,-2),则△ABC外接圆半径的长度为_______.
13.如图,等边三角形ABC内接于⊙O,P是BC上的任意一点.求证:PA=PB+PC.
14.如图,在△ABC中,AB=BC=2,以AB为直径的⊙O分别交BC、AC于点D、E,且点D为边BC的中点.
(1)求证:△ABC为等边三角形;
(2)求DE的长;
(3)在线段AB的延长线上是否存在一点P,使△PBD≌△AED 若存在,请求出PB的长;若不存在,请说明理由.
15.探究问题.
(1)阅读理解:
①如图①,若△ABC所在平面上存在一点P,使它到三角形三顶点的距离之和最小,则称点P为△ABC的费马点,此时PA+PB+PC的值为△ABC的费马距离.
②如图②,若四边形ABCD的四个顶点在同一个圆上,则有AB·CD+BC·AD=
AC·BD,此为托勒密定理.
(2)知识迁移:
①请你利用托勒密定理,解决如下问题:
如图③,已知点P为等边三角形ABC外接圆的上任意一点.求证:PB+PC=PA.
②根据(2)①的结论,我们有如下探寻三角形ABC(其中∠A、∠B、∠C均小于120°)的费马点和费马距离的方法:
第一步:如图④,在△ABC的外部以BC为边长作等边三角形BCD及其外接圆;
第二步:在上取一点P0,连接P0A、P0B、P0C、P0D.
易知P0A+P0B+P0C=P0A+(P0B+P0C)=P0A+_______;
第三步:请你根据(1)①中定义,在图④中找出△ABC的费马点P,线段_______的长度即为△ABC的费马距离.
(3)知识应用:
2012年4月,我国西南地区出现了罕见的持续干旱现象,许多村庄出现了人、畜饮水困难.为解决老百姓饮水问题,解放军某部到云南某地打井取水.
已知三村庄A、B、C构成了如图⑤所示的△ABC(其中∠A、∠B、∠C均小于120°),现选取一点P打水井,使水井P到三村庄A、B、C所铺设的输水管总长度最小.求输水管总长度的最小值.
参考答案
【基础巩固】
1.无数 无数 垂直平分线 不在同一直线上 一 一 2.外接圆 三边垂直平分线 三角形三个顶点 3.160° 4.D 5.A 6.C 7.半径为5,面积为25π 8~9.略
【拓展提优】
10.B 11.A 12. 13.略 14.(1)略 (2)DE=1 (3)存在.PB=1
15.(2)①略 ②P0D AD (3)5 km.
【基础巩固】
1.经过一点作圆可以作_______个圆;经过两点作圆可以作_______个圆,这些圆的圆心在这两点的_______上;经过_______的三点可以作_______个圆,并且只能作_______个圆.
2.三角形的外心是三角形的_______的圆心,它是三角形的_______的交点,它到_______的距离相等.
3.已知△ABC中,∠A=80°,若点O是△ABC的外心,则∠BOC=_______.
4.下列命题正确的是 ( )
A.三点确定一个圆
B.三角形的外心是三角形三个角的平分线的交点
C.圆有且只有一个内接三角形
D.三角形的外心是三角形任意两边的垂直平分线的交点
5.已知AB=7 cm,则过点A、B,且半径为3 cm的圆有 ( )
A.0个 B.1个 C.2个 D.无数个
6.下列四边形中,一定有外接圆的是 ( )
A.平行四边形 B.菱形 C.矩形 D.梯形
7.在Rt△ABC中,∠C=90°,若AC=6,BC=8,求Rt△ABC的外接圆的半径和面积.
8.(1)作四边形ABCD,使∠A=∠C=90°;
(2)经过点A、B、D作⊙O,⊙O是否经过点C 请说明理由.
9.活动与探究:
如图,CD所在的直线垂直平分线段AB.怎样使用这样的工具找到圆形工件的圆心?
【拓展提优】
10.如图,在5×5正方形网格中,一条圆弧经过A、B、C三点,那么这条弧所在圆的圆心是( )
A.点P B.点Q C.点R D.点M
11.已知直角三角形的一条直角边等于它的外接圆的半径,则这个直角三角形的面积与其外接圆的面积的比为 ( )
A.:2π B.:4π C.:π D.2:π
12.如图,△ABC的三个顶点的坐标分别为A(-1,3)、B(-2,-2)、C(4,-2),则△ABC外接圆半径的长度为_______.
13.如图,等边三角形ABC内接于⊙O,P是BC上的任意一点.求证:PA=PB+PC.
14.如图,在△ABC中,AB=BC=2,以AB为直径的⊙O分别交BC、AC于点D、E,且点D为边BC的中点.
(1)求证:△ABC为等边三角形;
(2)求DE的长;
(3)在线段AB的延长线上是否存在一点P,使△PBD≌△AED 若存在,请求出PB的长;若不存在,请说明理由.
15.探究问题.
(1)阅读理解:
①如图①,若△ABC所在平面上存在一点P,使它到三角形三顶点的距离之和最小,则称点P为△ABC的费马点,此时PA+PB+PC的值为△ABC的费马距离.
②如图②,若四边形ABCD的四个顶点在同一个圆上,则有AB·CD+BC·AD=
AC·BD,此为托勒密定理.
(2)知识迁移:
①请你利用托勒密定理,解决如下问题:
如图③,已知点P为等边三角形ABC外接圆的上任意一点.求证:PB+PC=PA.
②根据(2)①的结论,我们有如下探寻三角形ABC(其中∠A、∠B、∠C均小于120°)的费马点和费马距离的方法:
第一步:如图④,在△ABC的外部以BC为边长作等边三角形BCD及其外接圆;
第二步:在上取一点P0,连接P0A、P0B、P0C、P0D.
易知P0A+P0B+P0C=P0A+(P0B+P0C)=P0A+_______;
第三步:请你根据(1)①中定义,在图④中找出△ABC的费马点P,线段_______的长度即为△ABC的费马距离.
(3)知识应用:
2012年4月,我国西南地区出现了罕见的持续干旱现象,许多村庄出现了人、畜饮水困难.为解决老百姓饮水问题,解放军某部到云南某地打井取水.
已知三村庄A、B、C构成了如图⑤所示的△ABC(其中∠A、∠B、∠C均小于120°),现选取一点P打水井,使水井P到三村庄A、B、C所铺设的输水管总长度最小.求输水管总长度的最小值.
参考答案
【基础巩固】
1.无数 无数 垂直平分线 不在同一直线上 一 一 2.外接圆 三边垂直平分线 三角形三个顶点 3.160° 4.D 5.A 6.C 7.半径为5,面积为25π 8~9.略
【拓展提优】
10.B 11.A 12. 13.略 14.(1)略 (2)DE=1 (3)存在.PB=1
15.(2)①略 ②P0D AD (3)5 km.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
