青岛版 数学五年级下册 回顾整理——总复习 图形与几何 课件(共34张PPT)
文档属性
| 名称 | 青岛版 数学五年级下册 回顾整理——总复习 图形与几何 课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 13:12:27 | ||
图片预览




文档简介
(共34张PPT)
青岛版数学五年级(下)
回顾整理
——总复习
图形与几何
课堂导入
同学们,这一学期中,在图形与几何这一部分,我们都学习了哪些内容呢?
我会确定物体所在的位置了。
我们认识了长方体和正方体,还学习了表面积、体积的计算等。
小组交流:关于方向与位置主要学习了哪些内容?
知识回顾
方向与位置
用数对表示位置
用方向和距离描述简单的路线图
根据方向和距离确定物体的位置
(列数,行数)
要点回顾
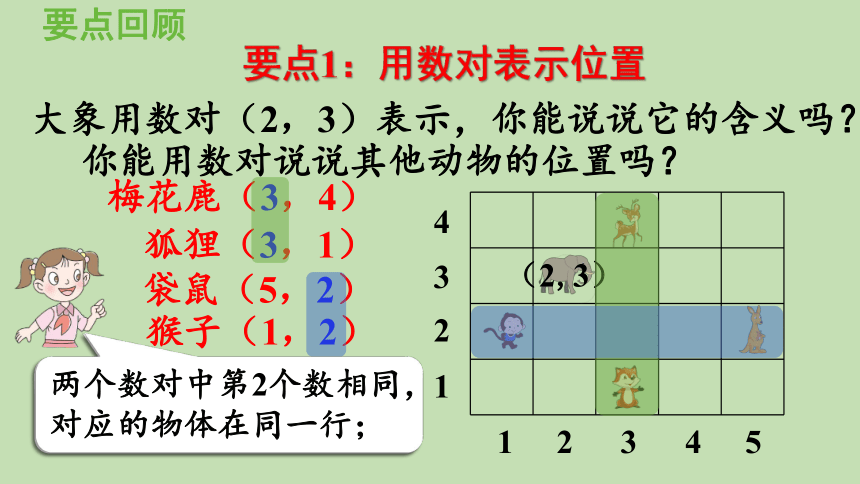
要点1:用数对表示位置
大象用数对(2,3)表示,你能说说它的含义吗?
2
3
1
1
2
3
4
5
4
你能用数对说说其他动物的位置吗?
(2,3)
猴子(1,2)
狐狸(3,1)
梅花鹿(3,4)
袋鼠(5,2)
两个数对中第1个数相同,对应的物体在同一列;
两个数对中第2个数相同,对应的物体在同一行;
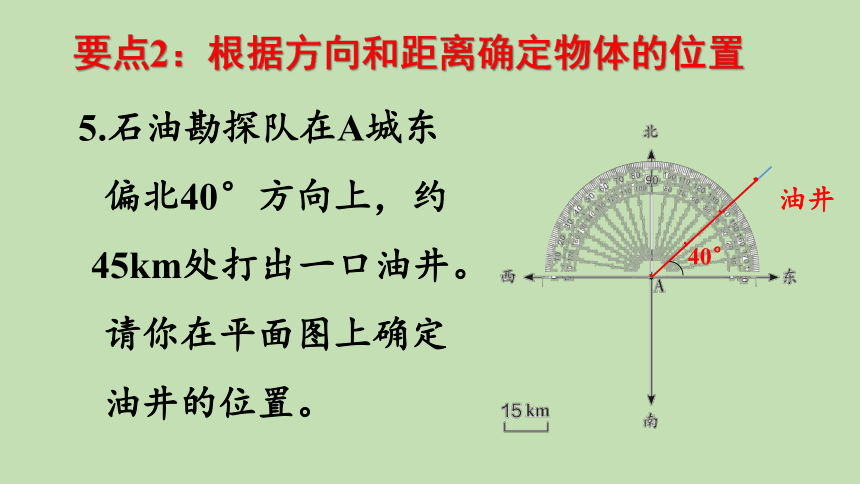
要点2:根据方向和距离确定物体的位置
5.石油勘探队在A城东偏北40°方向上,约
45km处打出一口油井。请你在平面图上确定油井的位置。
40°
油井
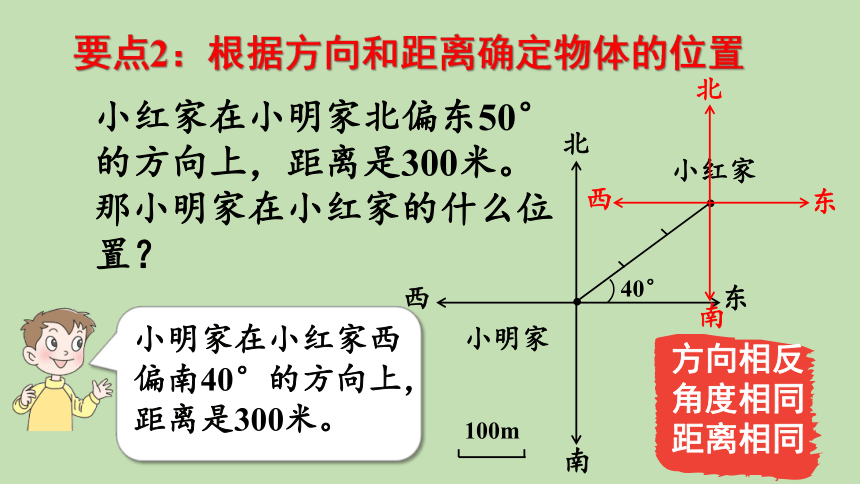
要点2:根据方向和距离确定物体的位置
东
北
西
南
小红家
小明家
100m
40°
小红家在小明家北偏东50°的方向上,距离是300米。那小明家在小红家的什么位置?
东
北
西
南
方向相反
角度相同
距离相同
小明家在小红家西偏南40°的方向上,距离是300米。
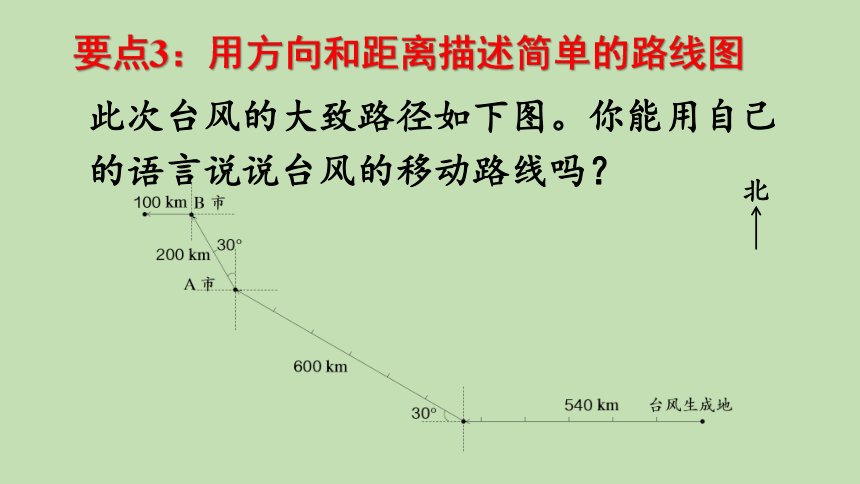
要点3:用方向和距离描述简单的路线图
此次台风的大致路径如下图。你能用自己的语言说说台风的移动路线吗?
北
北
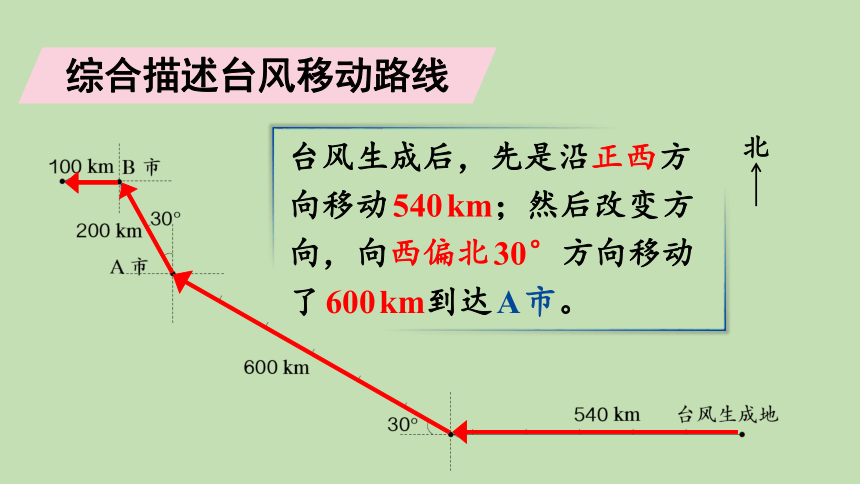
台风生成后,先是沿正西方向移动540km;然后改变方向,向西偏北30°方向移动了600km到达A市。
综合描述台风移动路线
北
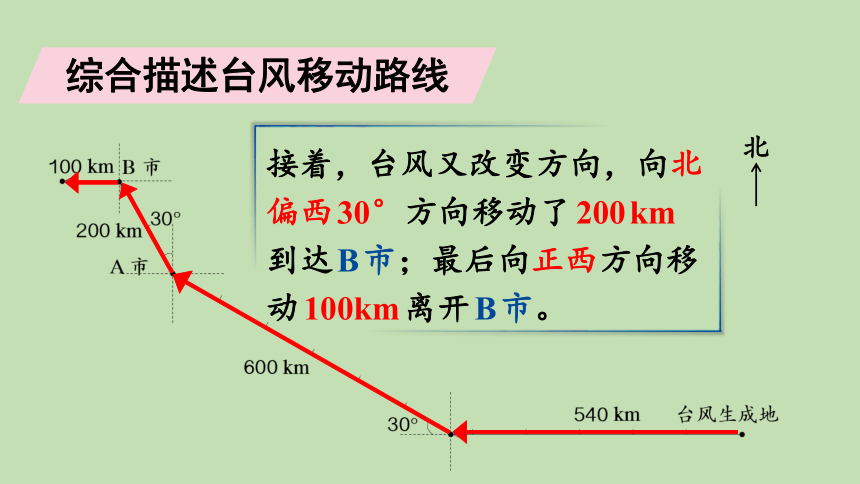
接着,台风又改变方向,向北偏西30°方向移动了200km到达B市;最后向正西方向移动100km离开B市。
综合描述台风移动路线
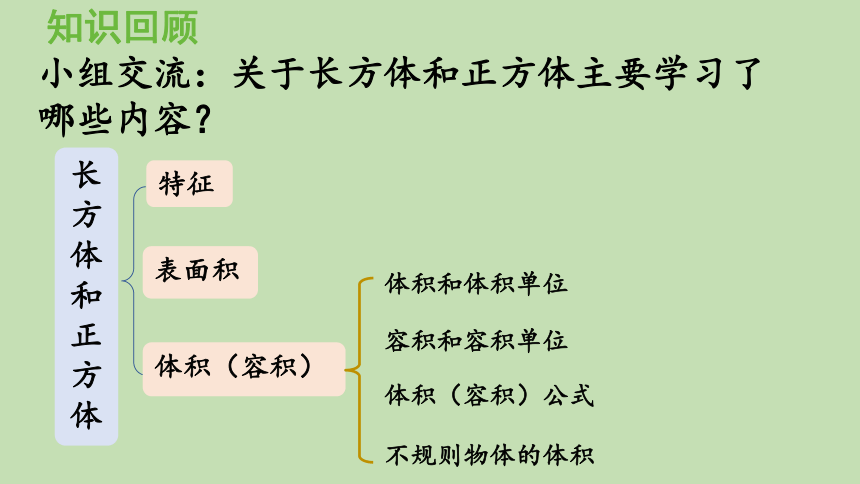
小组交流:关于长方体和正方体主要学习了哪些内容?
知识回顾
长方体和正方体
特征
体积(容积)
表面积
体积和体积单位
容积和容积单位
体积(容积)公式
不规则物体的体积
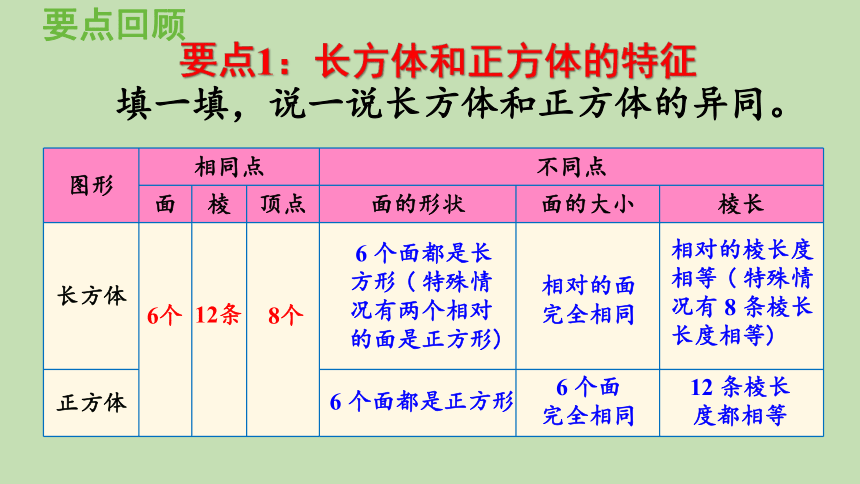
填一填,说一说长方体和正方体的异同。
图形 相同点 不同点 面 棱 顶点 面的形状 面的大小 棱长
长方体
正方体
6个
12条
8个
6 个面都是长方形 ( 特殊情况有两个相对的面是正方形)
相对的面
完全相同
相对的棱长度相等 ( 特殊情况有 8 条棱长长度相等)
6 个面都是正方形
6 个面
完全相同
12 条棱长度都相等
要点回顾
要点1:长方体和正方体的特征
如图是一个立体图形的展开图(单位:厘米)
10
10
10
5
5
(1)这个展开图可以折成( )体。
(2)折成的立体图形中长度是10cm的棱有( )条,棱长总和是( )cm。
(3)这个立体图形的表面积是( )cm 。
长方
8
120
240
要点2:长方体和正方体的表面积
长方体或正方体6个面的总面积,叫作它的表面积。长方体的表面积=(长×宽+长×高+宽×高)×2;正方体的表面积=棱长×棱长×6。
1 m =1000 dm 1 dm =1000 cm
1 L =1000 mL 1 dm = 1 L 1 cm = 1 mL
要点3:体积与容积
物体所占空间的大小叫作物体的体积。常用的体积单位有m 、dm 、cm 。
容器所能容纳物体的体积,通常叫作它的容积。常用的容积单位有L和mL。
(2)小长方体的个数 = 每行的个数×行数×层数
长方体的体积 = ( ) × ( ) × ( )
填一填,再说一说长方体体积公式的推导过程?
(1)如图所示的长方体是由棱长 1 cm的小正方体拼成的。这个长方体是由( )个这样的小正方体拼成的,它的长是( )cm,宽是( )cm,高是( )cm,它的体积是( )cm 。
30
5
3
2
30
5
3
2
长方体的体积=长×宽×高,用字母表示为:V=abh;正方体的体积=棱长×棱长×棱长,用字母表示:V=a·a·a=a 。长方体(或正方体)的体积=底面积×高,用字母表示: V=Sh。
要点4:体积(容积)计算公式
在解决表面积的实际问题中,要注意求的面的个数。
挖一个长8米、宽6米、深2米的蓄水池。
(1)如果给这个蓄水池的底面和四周抹上水泥,抹水泥部分的面积是多少平方米?
思路点拨
抹水泥的面积=底面的面积+侧面的面积
规范解答
8×6+(8×2+6×2)×2=104(m )
答:抹水泥部分的面积是104平方米。
要点5:表面积、体积(容积)的应用
在解决体积(容积)的实际问题中,要注意分清求的是体积还是容积。
挖一个长8米、宽6米、深2米的蓄水池。
要点5:表面积、体积(容积)的应用
(2)挖这个蓄水池,要挖土多少立方米?
思路点拨
挖土的体积 = 蓄水池的容积 = 长×宽×高
规范解答
8×6×2=96(m )
答:要挖土96立方米。
挖一个长8米、宽6米、深2米的蓄水池。
要点5:表面积、体积(容积)的应用
(3)蓄水时,当水面离蓄水池顶部还剩0.2m时就停止进水,这时已经蓄水多少吨?(1m 的水重1吨)
思路点拨
池内水的体积×1吨/m = 已经蓄水的吨数
规范解答
8×6×(2-0.2)×1=86.4(吨)
答:这时已经蓄水86.4吨。
350 cm =( )dm
2.06 m =( )dm
5.4 L=( )ml
20 dm =( )cm
0.24 dm =( )L( )ml
6500 ml=( )L( )ml
课堂练习
0.35
2060
5400
20000
0.24
240
6
500
(教材第112页“第12题” )
1.
(1)这排储物柜的占地面积是多少?
(2)这排储物柜所占的空间是多少立方米?
2×0.4=0.8(平方米)
2×0.4×1.2=0.96(立方米)
2.学校里有一排储物柜(如图)。
(教材第112页“第13题” )
5厘米=0.5分米
9×6×0.5=27(立方分米)
3.有一个长方体鱼缸(如右图),放进去一块珊瑚石(完全沉没),水面升高了5厘米。这块珊瑚石的体积是多少?
(教材第112页“第14题” )
答:这块珊瑚石的体积27立方分米。
至少需要8块小正方体木块
2×2×6=24(平方厘米)
2×2×2=8(立方厘米)
(教材第112页“第15题” )
4.用棱长1厘米的小正方体木块拼成一个正方体模型,至少要用多少块小正方体木块?这个正方体模型的表面积是多少平方厘米?体积是多少立方厘米?
答:表面积是24平方厘米。体积是8立方厘米。
177×177=31329(平方米)
(教材第112页“第16题” )
5.国家游泳中心“水立方”长177米,宽177米,高30米。
答:它的占地面积是31329平方米。
(1)它的占地面积是多少平方米?
(教材第112页“第16题” )
5.国家游泳中心“水立方”长177米,宽177米,高30米。
177×177+177×30×4=52569(平方米)
(2)它的表面所用的有机材料是多少平方米?
答:它的表面所用的有机材料是52569平方米。
(教材第112页“第16题” )
5.国家游泳中心“水立方”长177米,宽177米,高30米。
177×177×30=939870(立方米)
答:它的表面所用的有机材料是939870平方米。
(3)它的体积是多少立方米?
1.2×0.5×0.4=0.24(立方米)
0.24立方米=240立方分米=240升
6.这辆货车的油箱长
1.2米,宽0.5米,高
0.4米。(箱壁厚度忽略不计)
(1)这辆货车油箱的容积是多少升?
答:这辆货车油箱的容积是240升。
(教材第112页“第17题” )
100×(240÷40)=600(千米)
6.这辆货车的油箱长
1.2米,宽0.5米,高
0.4米。(箱壁厚度忽略不计)
(2)如果这辆货车每行驶100千米耗油40升,加满油后大约可以行驶多少千米?
答:加满油后大约可以行驶多少千米。
(教材第112页“第17题” )
7.下图是公园平面图。
(教材第112页“第18题” )
(1)用数对表示出民族风情园和游乐城的位置。
(2)李东现在的位置是(6,7),你知道他在哪儿吗?
(3)动物园在民族风情园的 偏 方向;公园大门在游乐城的 偏 方向。
(1,2)
(12,6)
动物园
北
东
45°
南
西
45°
(教材第112页“第18题” )
(4)从公园大门到水族馆可以怎么走?
答:从公园大门向北偏东45°方向走到游乐城,再向西走就可以到达水族馆;或者从公园大门向西走到民族风情园,再向北偏东45°方向走到动物园,然后向南偏东45°方向走到水族馆。
(教材第112页“第18题” )
8. 选一选。
(1)一个正方体木块,表面积是6平方分米,它的体积是( )。
A. 216立方分米 B. 18立方分米 C. 1立方分米
(2)一个长方体的长、宽、高分别是a米、b米、h米,如果高增加 2 米,新长方体的体积比原来增加( )立方米。
A. 2 ab B. 2 bh C. ab(h+2)
(3)下面三个体积中,与其他两个体积不同的是( )。
6.08m B. 6080000cm C. 608dm
C
C
A
3. 下面3个几何体都是由棱长1cm的小正方体摆成的。
①
②
③
(1)①、②、③的体积分别是多少?①的体积是③的体积的几分之几。
答:①的体积是6cm ,②的体积是10cm ,③的体积是11cm ; ①的体积是③的体积的6÷11= 。
11
6
3. 下面3个几何体都是由棱长1cm的小正方体摆成的。
①
②
③
(2)如果要把①、②、③分别继续补搭成一个大正方体,每个几何体至少还需要多少个小正方体?
答:把①补搭成棱长为4 cm的大正方体,需要4 -6=
58(个)小正方体;把②补搭成棱长为 4 cm的大正方体,需要4 -10=54(个)小正方体;把③补搭成棱长为3 cm的大正方体,需要3 -11=16(个)小正方体。
3. 下面3个几何体都是由棱长1cm的小正方体摆成的。
①
②
③
(3)你还能提出其他数学问题并解答吗?
(5+3+5)×2=26(cm )
①的表面积是多少?
答:①的表面积是26平方厘米。
相关练习。
02
01
课后练习题。
课后作业
青岛版数学五年级(下)
回顾整理
——总复习
图形与几何
课堂导入
同学们,这一学期中,在图形与几何这一部分,我们都学习了哪些内容呢?
我会确定物体所在的位置了。
我们认识了长方体和正方体,还学习了表面积、体积的计算等。
小组交流:关于方向与位置主要学习了哪些内容?
知识回顾
方向与位置
用数对表示位置
用方向和距离描述简单的路线图
根据方向和距离确定物体的位置
(列数,行数)
要点回顾
要点1:用数对表示位置
大象用数对(2,3)表示,你能说说它的含义吗?
2
3
1
1
2
3
4
5
4
你能用数对说说其他动物的位置吗?
(2,3)
猴子(1,2)
狐狸(3,1)
梅花鹿(3,4)
袋鼠(5,2)
两个数对中第1个数相同,对应的物体在同一列;
两个数对中第2个数相同,对应的物体在同一行;
要点2:根据方向和距离确定物体的位置
5.石油勘探队在A城东偏北40°方向上,约
45km处打出一口油井。请你在平面图上确定油井的位置。
40°
油井
要点2:根据方向和距离确定物体的位置
东
北
西
南
小红家
小明家
100m
40°
小红家在小明家北偏东50°的方向上,距离是300米。那小明家在小红家的什么位置?
东
北
西
南
方向相反
角度相同
距离相同
小明家在小红家西偏南40°的方向上,距离是300米。
要点3:用方向和距离描述简单的路线图
此次台风的大致路径如下图。你能用自己的语言说说台风的移动路线吗?
北
北
台风生成后,先是沿正西方向移动540km;然后改变方向,向西偏北30°方向移动了600km到达A市。
综合描述台风移动路线
北
接着,台风又改变方向,向北偏西30°方向移动了200km到达B市;最后向正西方向移动100km离开B市。
综合描述台风移动路线
小组交流:关于长方体和正方体主要学习了哪些内容?
知识回顾
长方体和正方体
特征
体积(容积)
表面积
体积和体积单位
容积和容积单位
体积(容积)公式
不规则物体的体积
填一填,说一说长方体和正方体的异同。
图形 相同点 不同点 面 棱 顶点 面的形状 面的大小 棱长
长方体
正方体
6个
12条
8个
6 个面都是长方形 ( 特殊情况有两个相对的面是正方形)
相对的面
完全相同
相对的棱长度相等 ( 特殊情况有 8 条棱长长度相等)
6 个面都是正方形
6 个面
完全相同
12 条棱长度都相等
要点回顾
要点1:长方体和正方体的特征
如图是一个立体图形的展开图(单位:厘米)
10
10
10
5
5
(1)这个展开图可以折成( )体。
(2)折成的立体图形中长度是10cm的棱有( )条,棱长总和是( )cm。
(3)这个立体图形的表面积是( )cm 。
长方
8
120
240
要点2:长方体和正方体的表面积
长方体或正方体6个面的总面积,叫作它的表面积。长方体的表面积=(长×宽+长×高+宽×高)×2;正方体的表面积=棱长×棱长×6。
1 m =1000 dm 1 dm =1000 cm
1 L =1000 mL 1 dm = 1 L 1 cm = 1 mL
要点3:体积与容积
物体所占空间的大小叫作物体的体积。常用的体积单位有m 、dm 、cm 。
容器所能容纳物体的体积,通常叫作它的容积。常用的容积单位有L和mL。
(2)小长方体的个数 = 每行的个数×行数×层数
长方体的体积 = ( ) × ( ) × ( )
填一填,再说一说长方体体积公式的推导过程?
(1)如图所示的长方体是由棱长 1 cm的小正方体拼成的。这个长方体是由( )个这样的小正方体拼成的,它的长是( )cm,宽是( )cm,高是( )cm,它的体积是( )cm 。
30
5
3
2
30
5
3
2
长方体的体积=长×宽×高,用字母表示为:V=abh;正方体的体积=棱长×棱长×棱长,用字母表示:V=a·a·a=a 。长方体(或正方体)的体积=底面积×高,用字母表示: V=Sh。
要点4:体积(容积)计算公式
在解决表面积的实际问题中,要注意求的面的个数。
挖一个长8米、宽6米、深2米的蓄水池。
(1)如果给这个蓄水池的底面和四周抹上水泥,抹水泥部分的面积是多少平方米?
思路点拨
抹水泥的面积=底面的面积+侧面的面积
规范解答
8×6+(8×2+6×2)×2=104(m )
答:抹水泥部分的面积是104平方米。
要点5:表面积、体积(容积)的应用
在解决体积(容积)的实际问题中,要注意分清求的是体积还是容积。
挖一个长8米、宽6米、深2米的蓄水池。
要点5:表面积、体积(容积)的应用
(2)挖这个蓄水池,要挖土多少立方米?
思路点拨
挖土的体积 = 蓄水池的容积 = 长×宽×高
规范解答
8×6×2=96(m )
答:要挖土96立方米。
挖一个长8米、宽6米、深2米的蓄水池。
要点5:表面积、体积(容积)的应用
(3)蓄水时,当水面离蓄水池顶部还剩0.2m时就停止进水,这时已经蓄水多少吨?(1m 的水重1吨)
思路点拨
池内水的体积×1吨/m = 已经蓄水的吨数
规范解答
8×6×(2-0.2)×1=86.4(吨)
答:这时已经蓄水86.4吨。
350 cm =( )dm
2.06 m =( )dm
5.4 L=( )ml
20 dm =( )cm
0.24 dm =( )L( )ml
6500 ml=( )L( )ml
课堂练习
0.35
2060
5400
20000
0.24
240
6
500
(教材第112页“第12题” )
1.
(1)这排储物柜的占地面积是多少?
(2)这排储物柜所占的空间是多少立方米?
2×0.4=0.8(平方米)
2×0.4×1.2=0.96(立方米)
2.学校里有一排储物柜(如图)。
(教材第112页“第13题” )
5厘米=0.5分米
9×6×0.5=27(立方分米)
3.有一个长方体鱼缸(如右图),放进去一块珊瑚石(完全沉没),水面升高了5厘米。这块珊瑚石的体积是多少?
(教材第112页“第14题” )
答:这块珊瑚石的体积27立方分米。
至少需要8块小正方体木块
2×2×6=24(平方厘米)
2×2×2=8(立方厘米)
(教材第112页“第15题” )
4.用棱长1厘米的小正方体木块拼成一个正方体模型,至少要用多少块小正方体木块?这个正方体模型的表面积是多少平方厘米?体积是多少立方厘米?
答:表面积是24平方厘米。体积是8立方厘米。
177×177=31329(平方米)
(教材第112页“第16题” )
5.国家游泳中心“水立方”长177米,宽177米,高30米。
答:它的占地面积是31329平方米。
(1)它的占地面积是多少平方米?
(教材第112页“第16题” )
5.国家游泳中心“水立方”长177米,宽177米,高30米。
177×177+177×30×4=52569(平方米)
(2)它的表面所用的有机材料是多少平方米?
答:它的表面所用的有机材料是52569平方米。
(教材第112页“第16题” )
5.国家游泳中心“水立方”长177米,宽177米,高30米。
177×177×30=939870(立方米)
答:它的表面所用的有机材料是939870平方米。
(3)它的体积是多少立方米?
1.2×0.5×0.4=0.24(立方米)
0.24立方米=240立方分米=240升
6.这辆货车的油箱长
1.2米,宽0.5米,高
0.4米。(箱壁厚度忽略不计)
(1)这辆货车油箱的容积是多少升?
答:这辆货车油箱的容积是240升。
(教材第112页“第17题” )
100×(240÷40)=600(千米)
6.这辆货车的油箱长
1.2米,宽0.5米,高
0.4米。(箱壁厚度忽略不计)
(2)如果这辆货车每行驶100千米耗油40升,加满油后大约可以行驶多少千米?
答:加满油后大约可以行驶多少千米。
(教材第112页“第17题” )
7.下图是公园平面图。
(教材第112页“第18题” )
(1)用数对表示出民族风情园和游乐城的位置。
(2)李东现在的位置是(6,7),你知道他在哪儿吗?
(3)动物园在民族风情园的 偏 方向;公园大门在游乐城的 偏 方向。
(1,2)
(12,6)
动物园
北
东
45°
南
西
45°
(教材第112页“第18题” )
(4)从公园大门到水族馆可以怎么走?
答:从公园大门向北偏东45°方向走到游乐城,再向西走就可以到达水族馆;或者从公园大门向西走到民族风情园,再向北偏东45°方向走到动物园,然后向南偏东45°方向走到水族馆。
(教材第112页“第18题” )
8. 选一选。
(1)一个正方体木块,表面积是6平方分米,它的体积是( )。
A. 216立方分米 B. 18立方分米 C. 1立方分米
(2)一个长方体的长、宽、高分别是a米、b米、h米,如果高增加 2 米,新长方体的体积比原来增加( )立方米。
A. 2 ab B. 2 bh C. ab(h+2)
(3)下面三个体积中,与其他两个体积不同的是( )。
6.08m B. 6080000cm C. 608dm
C
C
A
3. 下面3个几何体都是由棱长1cm的小正方体摆成的。
①
②
③
(1)①、②、③的体积分别是多少?①的体积是③的体积的几分之几。
答:①的体积是6cm ,②的体积是10cm ,③的体积是11cm ; ①的体积是③的体积的6÷11= 。
11
6
3. 下面3个几何体都是由棱长1cm的小正方体摆成的。
①
②
③
(2)如果要把①、②、③分别继续补搭成一个大正方体,每个几何体至少还需要多少个小正方体?
答:把①补搭成棱长为4 cm的大正方体,需要4 -6=
58(个)小正方体;把②补搭成棱长为 4 cm的大正方体,需要4 -10=54(个)小正方体;把③补搭成棱长为3 cm的大正方体,需要3 -11=16(个)小正方体。
3. 下面3个几何体都是由棱长1cm的小正方体摆成的。
①
②
③
(3)你还能提出其他数学问题并解答吗?
(5+3+5)×2=26(cm )
①的表面积是多少?
答:①的表面积是26平方厘米。
相关练习。
02
01
课后练习题。
课后作业
