6.2角（2）课件（共23张PPT）

(共23张PPT)
苏科版 七年级上册
6.2角(2)
教学目标：
1.会画一个角等于已知角
（两种方法）
2. 掌握角平分线概念；会用角平分线定义求有关角的运算
1.用量角器怎样测量角的大小
回顾旧知：
一对中 二合线 三读数
1.用量角器、直尺画一个角等于已知角
新知探究：
用一副三角板，可以拼出多少种不同的角？你能用手中的三角板画出150和105°的角吗？
新知探究：
用一副三角板，可以拼出多少种不同的角？你能用手中的三角板画出150和105°的角吗？
新知探究：
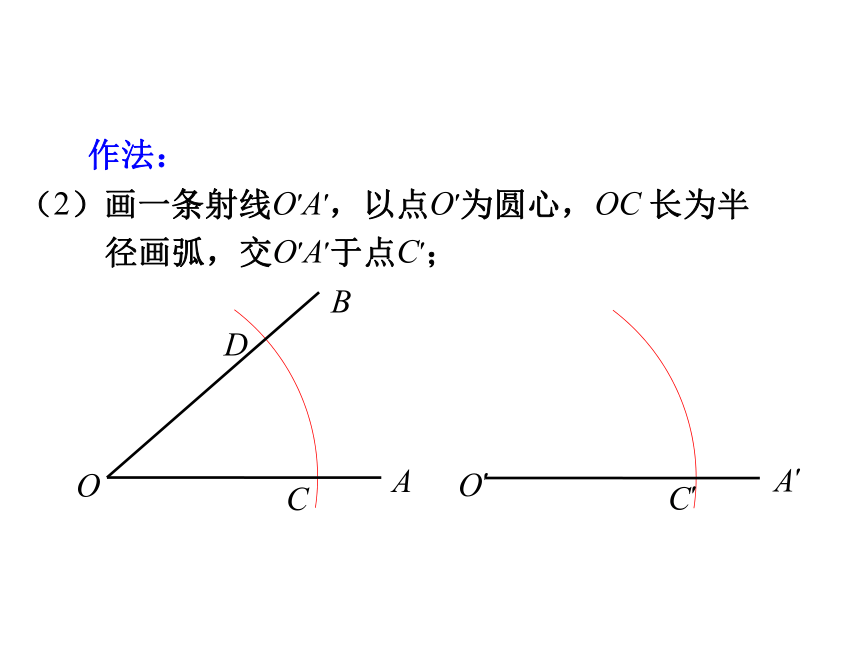
作法：
（1）以点O 为圆心，任意长为半径画弧，分别交OA，
OB 于点C、D；
　　已知：∠AOB．求作： ∠A′O′B′=∠AOB．
　　如何用尺规作一个角等于已知角？
O
D
B
C
A
新知探究：
作法：
（2）画一条射线O′A′，以点O′为圆心，OC 长为半
径画弧，交O′A′于点C′；
O′
C′
A′
O
D
B
C
A
作法：
（3）以点C′为圆心，CD 长为半径画弧，与第2 步中
所画的弧交于点D′；
O′
D′
C′
A′
O
D
B
C
A
作法：
（4）过点D′画射线O′B′，则∠A′O′B′=∠AOB．
O′
D′
B′
C′
A′
O
D
B
C
A
自主展示：
动动手：用纸片剪一个角，将角对折，折痕将角分成两个相等的角。
如图，如果∠AOB＝∠BOC,那么
∠AOC＝2∠AOB＝2 ,
∠AOB＝∠BOC＝ .
∠AOC
∠BOC
我们把射线OB叫做∠AOC的角平分线.
类比线段中点的定义，你能给角平分线下定义吗？
从一个角的顶点出发，把这个角分成相等的两个角的射线，叫这个角的平分线．
角平分线
角的平分线：
A
B
O
C
　从一个角的顶点出发，把这个角分成相等的两个角的射线，叫做这个角的平分线.
数学语言：
∵射线OC平分∠AOB
∴∠AOC=∠BOC= ∠AOB
1
2
或∠AOB=2∠AOC=2∠BOC
类似地：还有角的三等分线,如图
O
A
B
C
D
⌒
⌒
⌒
1
2
3
OB、OC是∠AOD的三等分线
例 如图，∠AOD=80°，OB是∠AOC的平分线，∠AOB=30°. 求∠AOC、∠COD的度数.
O
A
B
C
D
例题探究
解：由题可知,OB是∠AOC的平分线，
∠AOC＝2∠AOB
＝ 2 ×30°
＝ 60 .
∠COD＝∠AOD－∠AOC
＝80 －60
＝20
1．如图，∠AOB＝90 ，OC平分∠AOB，OE平分∠AOD，若∠EOC＝60 ，∠AOC＝ ， ∠AOE＝ , ∠EOD＝ ．
45
15
15
课堂练习
2.如图，O是直线AB上一点, OC是∠AOB的平分线， ∠COD=31 28′，求∠AOD的度数.
解：由题意可知，∠AOB是平角，
由OC是∠AOB的平分线可知，
∠AOC＝ ∠AOB
＝ ×180°
＝ 90 .
由∠AOC＝∠AOD＋∠COD可知，
∠AOD＝∠AOC－∠COD
＝90 －31 28′
＝58 32′.
检测反馈：
1.（2分）利用一副三角板上已知度数的角，不能画出的角是（ ）
A.15° B.135°C.165° D.100°
2.（2分）如图，OC是∠AOB的平分线，若∠AOC＝75°，则∠AOB的度数为(　　)
A．145° B．150° C．155° D．160°
3．（2分）已知OC在∠AOB的内部，下列给出的条件中，不能得到OC为∠AOB的平分线的是( )
A．∠AOC＝2(1)∠AOB B．∠AOB＝2∠BOC
C．∠AOC＋∠COB＝∠AOB D．∠AOC＝∠BOC.
4.（4分）如图，如果∠AOD=76°，OC是∠ AOD内的一条射线，OB是∠AOC的平分线，
∠AOB= 30°.求∠AOC与∠COD的度数.
1、尺规作图：如何作一个角等于已知角
2、角的平分线：
　从一个角的顶点出发，把这个角分成相等的两个角的射线，叫做这个角的平分线.
课堂小结：
课后作业：
课本157页习题6.2—
4、7、8.
谢 谢！