人教版 数学六年级上册 专项突破练习之应用题(含答案)
文档属性
| 名称 | 人教版 数学六年级上册 专项突破练习之应用题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 267.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 14:44:32 | ||
图片预览




文档简介
人教版六年级上册数学期末专项突破练习之应用题
1.狮子的寿命大约是21年,老虎的寿命是狮子的,刺猬的寿命是老虎的,刺猬的寿命是多少年?
2.今年妈妈的年龄是42岁,女儿的年龄比妈妈少,女儿今年几岁?
3.(10分)在平面图上标出各场所的位置。
(1)学校在少年宫北偏东30°的方向2000米处。
(2)图书馆在少年宫西偏南45°方向1000米处。
(3)购物中心在少年宫西偏北40°方向1500米处。
(4)体育馆在少年宫东偏北25°方向2500米处。
(5)邮局在少年宫南偏东35°方向2000米处。
4.根据小东从家到书店的路线图填写下表。
方向 路程 时间
小东家→超市 7分钟
超市→邮局 11分钟
邮局→广场 7分钟
广场→体育馆 11分钟
体育馆→书店 14分钟
小东从家到书店的平均速度是多少?
5.大齿轮有100个齿,每分钟转25转;小齿轮有25个齿,每分钟转100转.
(1)写出大齿轮和小齿轮齿数的比,并求出比值.
(2)写出大齿轮和小齿轮每分钟转数的比,并求出比值.
6.一个长方形,它的周长是36cm,长宽的比是7:2,这个长方形的面积是多少平方厘米.
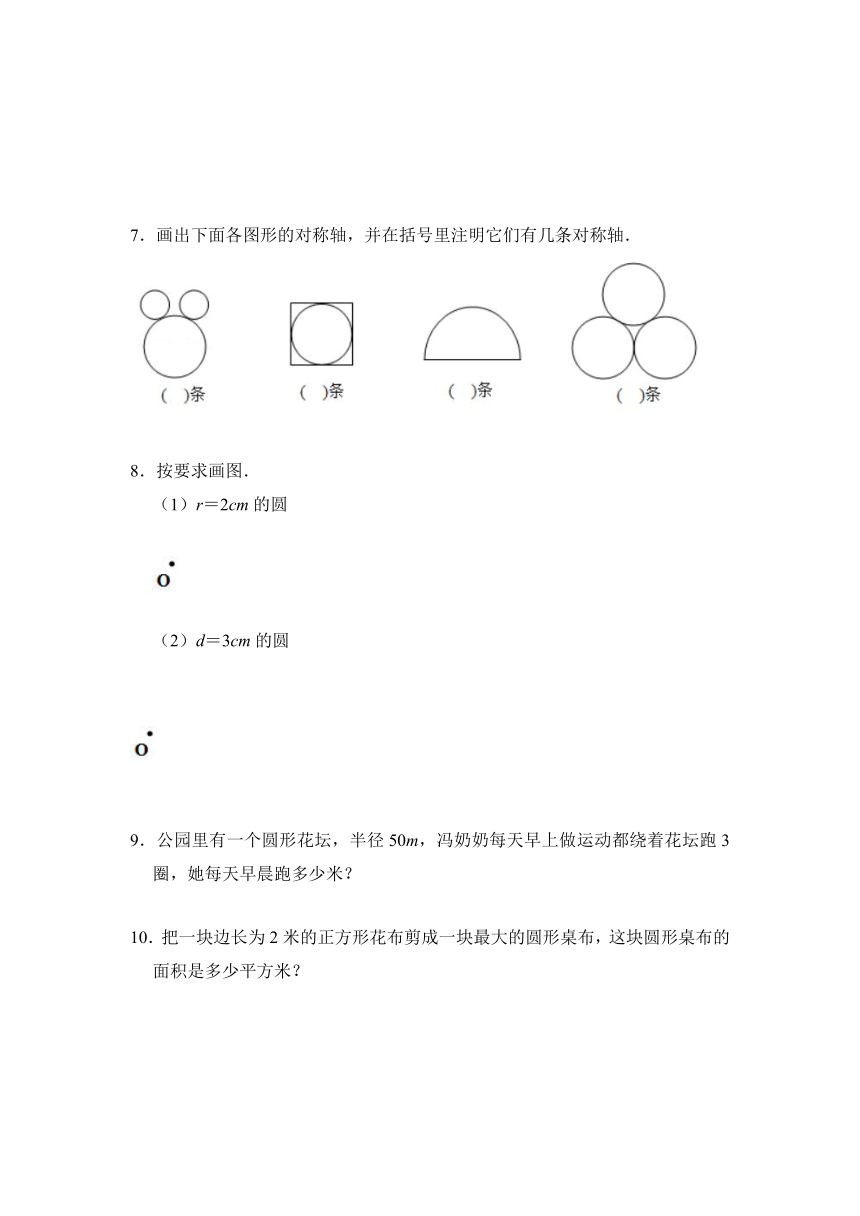
7.画出下面各图形的对称轴,并在括号里注明它们有几条对称轴.
8.按要求画图.
(1)r=2cm的圆
(2)d=3cm的圆
9.公园里有一个圆形花坛,半径50m,冯奶奶每天早上做运动都绕着花坛跑3圈,她每天早晨跑多少米?
10.把一块边长为2米的正方形花布剪成一块最大的圆形桌布,这块圆形桌布的面积是多少平方米?
11.一捆电线在半径为0.1米的圆筒上绕了30圈,这捆电线大约长多少米?
答案
1.狮子的寿命大约是21年,老虎的寿命是狮子的,刺猬的寿命是老虎的,刺猬的寿命是多少年?
【分析】把狮子的寿命看作单位“1”,用狮子的寿命乘就是老虎的寿命,把老虎的寿命看作单位“1”,用老虎的寿命乘就是刺猬的寿命,据此即可解答.
【解答】解:21××
=19×
=5(年)
答:刺猬的寿命是5年.
2.今年妈妈的年龄是42岁,女儿的年龄比妈妈少,女儿今年几岁?
【分析】今年妈妈的年龄是42岁,女儿的年龄比妈妈少,即女儿年龄是妈妈的1﹣,根据分数乘法的意义,用妈妈年龄乘女儿占妈妈年龄的分率,即得女儿多少岁.
【解答】解:42×(1﹣)
=42×
=14(岁)
答:女儿今年14岁.
3.在平面图上标出各场所的位置。
(1)学校在少年宫北偏东30°的方向2000米处。
(2)图书馆在少年宫西偏南45°方向1000米处。
(3)购物中心在少年宫西偏北40°方向1500米处。
(4)体育馆在少年宫东偏北25°方向2500米处。
(5)邮局在少年宫南偏东35°方向2000米处。
【分析】(1)学校在少年宫北偏东30°的方向,距离2000÷500=4(个)单位长度;
(2)图书馆在少年宫西偏南45°方向,距离1000÷500=2(个)单位长度;
(3)购物中心在少年宫西偏北40°方向,距离1500÷500=3(个)单位长度;
(4)体育馆在少年宫东偏北25°方向,距离2500÷500=5(个)单位长度;
(5)邮局在少年宫南偏东35°方向,距离2000÷500=4(个)单位长度。
【解答】解:根据题意作图如下:
4.根据小东从家到书店的路线图填写下表。
方向 路程 时间
小东家→超市 7分钟
超市→邮局 11分钟
邮局→广场 7分钟
广场→体育馆 11分钟
体育馆→书店 14分钟
小东从家到书店的平均速度是多少?
【分析】根据图上确定方向的方法:上北下南、左西右东确定方向,利用比例尺和图上距离,计算实际距离,结合图示角度完成统计表。
【解答】解:300×2=600(米)
300×3=900(米)
300×4=1200(米)
如表:
方向 路程 时间
小东家→超市 北偏东35° 600 7分钟
超市→邮局 东偏南30° 900 11分钟
邮局→广场 东 600 7分钟
广场→体育馆 东偏北25° 900 11分钟
体育馆→书店 东偏南35° 1200 14分钟
(600+900+600+900+1200)÷(7+11+7+11+14)
=4200÷50
=84(米/分)
答:小东从家到书店的平均速度是84米/分。
5.大齿轮有100个齿,每分钟转25转;小齿轮有25个齿,每分钟转100转.
(1)写出大齿轮和小齿轮齿数的比,并求出比值.
(2)写出大齿轮和小齿轮每分钟转数的比,并求出比值.
【分析】(1)大齿轮齿数比小齿轮齿数即可,用比的前项除以后项求出比值;
(2)大齿轮每分钟转数比小齿轮每分钟转数即可,用比的前项除以后项求出比值.
【解答】解:(1)100:25=4:1;
4:1=4÷1=4;
答:大齿轮和小齿轮齿数的比是4:1,比值是4.
(2)25:100=1:4,
1:4=1÷4=;
答:大齿轮和小齿轮每分钟转数的比是1:4,比值是.
6.一个长方形,它的周长是36cm,长宽的比是7:2,这个长方形的面积是 56 平方厘米.
【分析】根据长方形的特征,对边平行且相等,已知周长和长与宽的比,首先利用按比例分配的方法求出长、宽,再根据长方形的面积=长×宽,列式解答.
【解答】解:7+2=9(份),
长:36÷2×=18×=14(厘米),
宽:36÷2×=18×=4(厘米),
面积:14×4=56(平方厘米);
答:这个长方形的面积是56平方厘米.
故答案为:56.
7.画出下面各图形的对称轴,并在括号里注明它们有几条对称轴.
【分析】一个图形沿一条直线对折,直线两旁的部分能够完全重合,那么这个图形就是轴对称图形,这条直线就是这个图形的对称轴.根据轴对称图形的定义,找出并画出轴对称图形的对称轴即可.
【解答】解:根据轴对称图形的定义可以找出上述图形的对称轴,并把它们画出来,如下图所示:
8.按要求画图.
(1)r=2cm的圆
(2)d=3cm的圆
【分析】圆心决定圆的位置,半径决定圆的大小,先制定好圆规两脚之间的距离,即以已知线段长为圆规两脚之间的距离,然后以已知点O为圆心,以已知线段r长为半径画圆即可.
【解答】解:画圆如下:
(1)r=2cm的圆
(2)d=3cm的圆,即r=1.5cm
9.公园里有一个圆形花坛,半径50m,冯奶奶每天早上做运动都绕着花坛跑3圈,她每天早晨跑多少米?
【分析】根据圆的周长公式:c=2πr,把数据代入公式求出花坛的周长,然后乘3即为每天早晨跑多少米.
【解答】解:2×3.14×50×3
=314×30
=942(米)
答:她每天早晨跑942米.
10.把一块边长为2米的正方形花布剪成一块最大的圆形桌布,这块圆形桌布的面积是多少平方米?
【分析】根据题意可知,正方形的边长为最大圆的直径,然后再用圆的直径除以2计算出最大圆的半径,最后再根据圆的面积公式进行计算即可得到答案.
【解答】解:3.14×(2÷2)2
=3.14×1
=3.14(平方米)
答:这块圆形桌布的面积是3.14平方米.
11.一捆电线在半径为0.1米的圆筒上绕了30圈,这捆电线大约长多少米?
【分析】利用圆的周长公式C=2πr计算出每圈电线的长度,然后再乘30圈就是这一捆电线的总长,据此解答即可.
【解答】解:2×3.14×0.1×30
=3.14×6
=18.84(米)
答:这捆电线大约长18.84米
1.狮子的寿命大约是21年,老虎的寿命是狮子的,刺猬的寿命是老虎的,刺猬的寿命是多少年?
2.今年妈妈的年龄是42岁,女儿的年龄比妈妈少,女儿今年几岁?
3.(10分)在平面图上标出各场所的位置。
(1)学校在少年宫北偏东30°的方向2000米处。
(2)图书馆在少年宫西偏南45°方向1000米处。
(3)购物中心在少年宫西偏北40°方向1500米处。
(4)体育馆在少年宫东偏北25°方向2500米处。
(5)邮局在少年宫南偏东35°方向2000米处。
4.根据小东从家到书店的路线图填写下表。
方向 路程 时间
小东家→超市 7分钟
超市→邮局 11分钟
邮局→广场 7分钟
广场→体育馆 11分钟
体育馆→书店 14分钟
小东从家到书店的平均速度是多少?
5.大齿轮有100个齿,每分钟转25转;小齿轮有25个齿,每分钟转100转.
(1)写出大齿轮和小齿轮齿数的比,并求出比值.
(2)写出大齿轮和小齿轮每分钟转数的比,并求出比值.
6.一个长方形,它的周长是36cm,长宽的比是7:2,这个长方形的面积是多少平方厘米.
7.画出下面各图形的对称轴,并在括号里注明它们有几条对称轴.
8.按要求画图.
(1)r=2cm的圆
(2)d=3cm的圆
9.公园里有一个圆形花坛,半径50m,冯奶奶每天早上做运动都绕着花坛跑3圈,她每天早晨跑多少米?
10.把一块边长为2米的正方形花布剪成一块最大的圆形桌布,这块圆形桌布的面积是多少平方米?
11.一捆电线在半径为0.1米的圆筒上绕了30圈,这捆电线大约长多少米?
答案
1.狮子的寿命大约是21年,老虎的寿命是狮子的,刺猬的寿命是老虎的,刺猬的寿命是多少年?
【分析】把狮子的寿命看作单位“1”,用狮子的寿命乘就是老虎的寿命,把老虎的寿命看作单位“1”,用老虎的寿命乘就是刺猬的寿命,据此即可解答.
【解答】解:21××
=19×
=5(年)
答:刺猬的寿命是5年.
2.今年妈妈的年龄是42岁,女儿的年龄比妈妈少,女儿今年几岁?
【分析】今年妈妈的年龄是42岁,女儿的年龄比妈妈少,即女儿年龄是妈妈的1﹣,根据分数乘法的意义,用妈妈年龄乘女儿占妈妈年龄的分率,即得女儿多少岁.
【解答】解:42×(1﹣)
=42×
=14(岁)
答:女儿今年14岁.
3.在平面图上标出各场所的位置。
(1)学校在少年宫北偏东30°的方向2000米处。
(2)图书馆在少年宫西偏南45°方向1000米处。
(3)购物中心在少年宫西偏北40°方向1500米处。
(4)体育馆在少年宫东偏北25°方向2500米处。
(5)邮局在少年宫南偏东35°方向2000米处。
【分析】(1)学校在少年宫北偏东30°的方向,距离2000÷500=4(个)单位长度;
(2)图书馆在少年宫西偏南45°方向,距离1000÷500=2(个)单位长度;
(3)购物中心在少年宫西偏北40°方向,距离1500÷500=3(个)单位长度;
(4)体育馆在少年宫东偏北25°方向,距离2500÷500=5(个)单位长度;
(5)邮局在少年宫南偏东35°方向,距离2000÷500=4(个)单位长度。
【解答】解:根据题意作图如下:
4.根据小东从家到书店的路线图填写下表。
方向 路程 时间
小东家→超市 7分钟
超市→邮局 11分钟
邮局→广场 7分钟
广场→体育馆 11分钟
体育馆→书店 14分钟
小东从家到书店的平均速度是多少?
【分析】根据图上确定方向的方法:上北下南、左西右东确定方向,利用比例尺和图上距离,计算实际距离,结合图示角度完成统计表。
【解答】解:300×2=600(米)
300×3=900(米)
300×4=1200(米)
如表:
方向 路程 时间
小东家→超市 北偏东35° 600 7分钟
超市→邮局 东偏南30° 900 11分钟
邮局→广场 东 600 7分钟
广场→体育馆 东偏北25° 900 11分钟
体育馆→书店 东偏南35° 1200 14分钟
(600+900+600+900+1200)÷(7+11+7+11+14)
=4200÷50
=84(米/分)
答:小东从家到书店的平均速度是84米/分。
5.大齿轮有100个齿,每分钟转25转;小齿轮有25个齿,每分钟转100转.
(1)写出大齿轮和小齿轮齿数的比,并求出比值.
(2)写出大齿轮和小齿轮每分钟转数的比,并求出比值.
【分析】(1)大齿轮齿数比小齿轮齿数即可,用比的前项除以后项求出比值;
(2)大齿轮每分钟转数比小齿轮每分钟转数即可,用比的前项除以后项求出比值.
【解答】解:(1)100:25=4:1;
4:1=4÷1=4;
答:大齿轮和小齿轮齿数的比是4:1,比值是4.
(2)25:100=1:4,
1:4=1÷4=;
答:大齿轮和小齿轮每分钟转数的比是1:4,比值是.
6.一个长方形,它的周长是36cm,长宽的比是7:2,这个长方形的面积是 56 平方厘米.
【分析】根据长方形的特征,对边平行且相等,已知周长和长与宽的比,首先利用按比例分配的方法求出长、宽,再根据长方形的面积=长×宽,列式解答.
【解答】解:7+2=9(份),
长:36÷2×=18×=14(厘米),
宽:36÷2×=18×=4(厘米),
面积:14×4=56(平方厘米);
答:这个长方形的面积是56平方厘米.
故答案为:56.
7.画出下面各图形的对称轴,并在括号里注明它们有几条对称轴.
【分析】一个图形沿一条直线对折,直线两旁的部分能够完全重合,那么这个图形就是轴对称图形,这条直线就是这个图形的对称轴.根据轴对称图形的定义,找出并画出轴对称图形的对称轴即可.
【解答】解:根据轴对称图形的定义可以找出上述图形的对称轴,并把它们画出来,如下图所示:
8.按要求画图.
(1)r=2cm的圆
(2)d=3cm的圆
【分析】圆心决定圆的位置,半径决定圆的大小,先制定好圆规两脚之间的距离,即以已知线段长为圆规两脚之间的距离,然后以已知点O为圆心,以已知线段r长为半径画圆即可.
【解答】解:画圆如下:
(1)r=2cm的圆
(2)d=3cm的圆,即r=1.5cm
9.公园里有一个圆形花坛,半径50m,冯奶奶每天早上做运动都绕着花坛跑3圈,她每天早晨跑多少米?
【分析】根据圆的周长公式:c=2πr,把数据代入公式求出花坛的周长,然后乘3即为每天早晨跑多少米.
【解答】解:2×3.14×50×3
=314×30
=942(米)
答:她每天早晨跑942米.
10.把一块边长为2米的正方形花布剪成一块最大的圆形桌布,这块圆形桌布的面积是多少平方米?
【分析】根据题意可知,正方形的边长为最大圆的直径,然后再用圆的直径除以2计算出最大圆的半径,最后再根据圆的面积公式进行计算即可得到答案.
【解答】解:3.14×(2÷2)2
=3.14×1
=3.14(平方米)
答:这块圆形桌布的面积是3.14平方米.
11.一捆电线在半径为0.1米的圆筒上绕了30圈,这捆电线大约长多少米?
【分析】利用圆的周长公式C=2πr计算出每圈电线的长度,然后再乘30圈就是这一捆电线的总长,据此解答即可.
【解答】解:2×3.14×0.1×30
=3.14×6
=18.84(米)
答:这捆电线大约长18.84米
