高一数学《空间向量与立体几何》小结与复习课件
文档属性
| 名称 | 高一数学《空间向量与立体几何》小结与复习课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 877.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-16 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
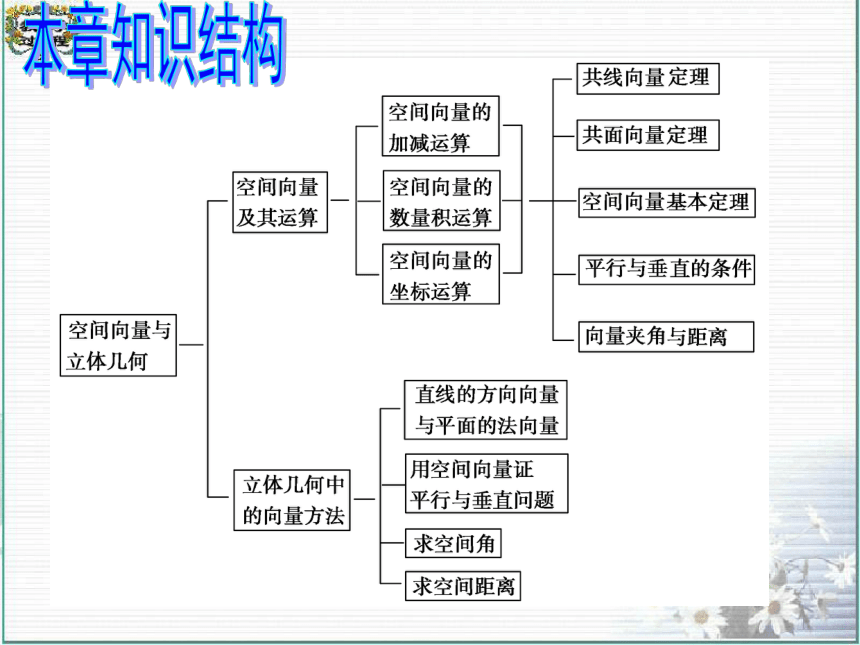
第三章
空间向量与立体几何
小结与复习
归纳整理
归纳整理
8.如果表示空间向量的有向线段所在的直线互相平行或重合,则这些向量叫做共线向量或平行向量。
9.平行于同一平面的向量,叫做共面向量
10.平面的法向量:如果表示向量 的有向线段所在直线垂直于平面 ,则称这个向量垂直于平面 ,记作 ⊥ ,如果 ⊥ ,那 么 向 量 叫做平面 的法向量.
(二)空间向量的运算
1.加法:三角形法则或平行四边形法则
2.减法:三角形法则
加法交换律
加法结合律
注:两个空间向量的加、减法与两个平面向量的加、
减法实质是一样的.三个向量或三个以上向量的和
遵循空间多边形法则
空间向量的数乘运算满足分配律及结合律
4、两个向量的数量积
注:①两个向量的数量积是数量,而不是向量.
②规定:零向量与任意向量的数量积等于零.
空间两个向量的数量积的性质
注:空间向量的数量积具有和平面向量的数量积完全相同的性质.
1.共线向量定理:对空间任意两个向量
的充要条件是存在实数 使
2、平面向量基本定理 如果e1和e2是一平面内的两个不平行的向量,那么,该平面内的任一向量a,存在惟一的一对实数a1,a2,使 a= a1 e1 +a2 e2
(三)空间向量的理论
O
A
B
P
a
若P为A,B中点,
则
向量参数表示式
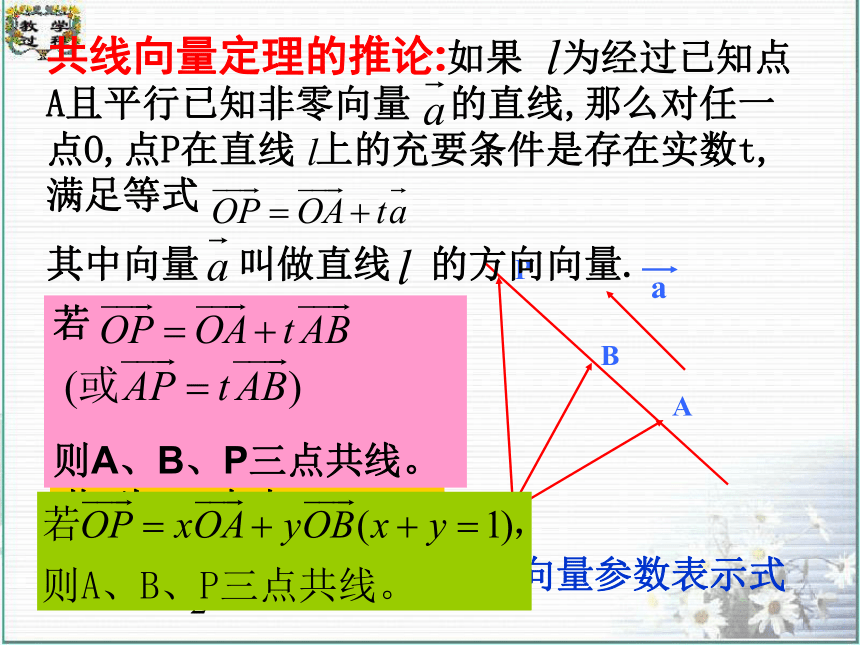
共线向量定理的推论:如果 为经过已知点A且平行已知非零向量 的直线,那么对任一点O,点P在直线 上的充要条件是存在实数t,满足等式
其中向量 叫做直线 的方向向量.
若
则A、B、P三点共线。
结论:空间一点P位于平面ABC内
存在有序实数对x,y使
可证明或判断四点共面
或对空间任一点O,有
共面向量定理的推论:
4.空间向量基本定理 若三个向量a,b,c不共面,则对空间任一向量p,存在有序实数组{x,y,z},使得p=xa+yb+zc.
其中{a,b,c}叫做空间的一个基底,a,b,c都叫做基向量
若空间向量的一个基底中的三个基向量互相垂直,则称这个
基底为正交基底,若三个基向量是互相垂直的单位向量,则称这
个基底为单位正交基底
共线向量 共面向量
定义 向量所在直线互相平行或重合 平行于同一平面的向量,叫做共面向量.
定理
推论
运用 判断三点共线,或两直线平行 判断四点共面,或直线平行于平面
小结
共面
(四)空间向量运算的坐标表示
(1)若p=xe1+ye2+ze3,则p=(x,y,z).
(2)设{i,j,k}为单位正交基底,向量a=(x1,y1,z1),b=(x2,y2,z2).
a+b=(x1+x2,y1+y2,z1+z2)
a-b=(x1-x2,y1-y2,z1-z2)
λa=(λx1,λy1,λz1)
a·b=x1x2+y1y2+z1z2
x1=λx2,y1=λy2,z1=λz2(λ∈R)
a//b
a⊥b
x1x2+y1y2+z1z2 =0
|a|=
(五)、空间线面位置关系的向量法:
异面直线所成角的范围:
思考:
结论:
1、线线角:
(六)、空间角的向量方法:
斜线与平面所成的角
平面的一条斜线
和它在这个平面内的射影
所成的锐角
A
O
B
2、线面角
当直线与平面垂直时,直
线与平面所成的角是90°
当直线在平面内或
与平面平行时,
直线与平面所成的角是0°
斜线与平面所成的角
( 0°, 90°)
直线与平面所成的角
[ 0°, 90°]
异面直线所成的角
( 0°, 90°]
n
A
B
线面角或等于直线的方向向量与平面的法向量所成角的补角的余角.
2、线面角向量法:
范围:
线面角等于直线的方向向量与平面的法向量所成角 的余角.
O
B
A
A
B
从一条直线出发的两个半平面所组成的图形叫做二面角。
这条直线叫做二面角的棱。
这两个半平面叫做二面角的面。
3
定义:
2、二面角
二面角的平面角必须满足:
3)角的边都要垂直于二面角的棱
1)角的顶点在棱上
2)角的两边分别在两个面内
以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角。
10
l
O
A
B
l
l
3、二面角的向量方法:
二面角的范围:
①向量法
注意法向量的方向:一进一出,二面角等于法向量夹角;
同进同出,二面角等于法向量夹角的补角
(六)、空间角的向量方法:
(七)空间“距离”问题
1. 空间两点之间的距离
根据两向量数量积的性质和坐标运算,
利用公式 或
(其中 ) ,可将两点距离问题
转化为求向量模长问题
2、E为平面α外一点,F为α内任意一 点, 为平面α的法向量,则点E到平面的距离为:
3、a,b是异面直线,E,F分别是直线a,b上的点, 是a,b公垂线的方向向量,则a,b间距离为
第三章
空间向量与立体几何
小结与复习
归纳整理
归纳整理
8.如果表示空间向量的有向线段所在的直线互相平行或重合,则这些向量叫做共线向量或平行向量。
9.平行于同一平面的向量,叫做共面向量
10.平面的法向量:如果表示向量 的有向线段所在直线垂直于平面 ,则称这个向量垂直于平面 ,记作 ⊥ ,如果 ⊥ ,那 么 向 量 叫做平面 的法向量.
(二)空间向量的运算
1.加法:三角形法则或平行四边形法则
2.减法:三角形法则
加法交换律
加法结合律
注:两个空间向量的加、减法与两个平面向量的加、
减法实质是一样的.三个向量或三个以上向量的和
遵循空间多边形法则
空间向量的数乘运算满足分配律及结合律
4、两个向量的数量积
注:①两个向量的数量积是数量,而不是向量.
②规定:零向量与任意向量的数量积等于零.
空间两个向量的数量积的性质
注:空间向量的数量积具有和平面向量的数量积完全相同的性质.
1.共线向量定理:对空间任意两个向量
的充要条件是存在实数 使
2、平面向量基本定理 如果e1和e2是一平面内的两个不平行的向量,那么,该平面内的任一向量a,存在惟一的一对实数a1,a2,使 a= a1 e1 +a2 e2
(三)空间向量的理论
O
A
B
P
a
若P为A,B中点,
则
向量参数表示式
共线向量定理的推论:如果 为经过已知点A且平行已知非零向量 的直线,那么对任一点O,点P在直线 上的充要条件是存在实数t,满足等式
其中向量 叫做直线 的方向向量.
若
则A、B、P三点共线。
结论:空间一点P位于平面ABC内
存在有序实数对x,y使
可证明或判断四点共面
或对空间任一点O,有
共面向量定理的推论:
4.空间向量基本定理 若三个向量a,b,c不共面,则对空间任一向量p,存在有序实数组{x,y,z},使得p=xa+yb+zc.
其中{a,b,c}叫做空间的一个基底,a,b,c都叫做基向量
若空间向量的一个基底中的三个基向量互相垂直,则称这个
基底为正交基底,若三个基向量是互相垂直的单位向量,则称这
个基底为单位正交基底
共线向量 共面向量
定义 向量所在直线互相平行或重合 平行于同一平面的向量,叫做共面向量.
定理
推论
运用 判断三点共线,或两直线平行 判断四点共面,或直线平行于平面
小结
共面
(四)空间向量运算的坐标表示
(1)若p=xe1+ye2+ze3,则p=(x,y,z).
(2)设{i,j,k}为单位正交基底,向量a=(x1,y1,z1),b=(x2,y2,z2).
a+b=(x1+x2,y1+y2,z1+z2)
a-b=(x1-x2,y1-y2,z1-z2)
λa=(λx1,λy1,λz1)
a·b=x1x2+y1y2+z1z2
x1=λx2,y1=λy2,z1=λz2(λ∈R)
a//b
a⊥b
x1x2+y1y2+z1z2 =0
|a|=
(五)、空间线面位置关系的向量法:
异面直线所成角的范围:
思考:
结论:
1、线线角:
(六)、空间角的向量方法:
斜线与平面所成的角
平面的一条斜线
和它在这个平面内的射影
所成的锐角
A
O
B
2、线面角
当直线与平面垂直时,直
线与平面所成的角是90°
当直线在平面内或
与平面平行时,
直线与平面所成的角是0°
斜线与平面所成的角
( 0°, 90°)
直线与平面所成的角
[ 0°, 90°]
异面直线所成的角
( 0°, 90°]
n
A
B
线面角或等于直线的方向向量与平面的法向量所成角的补角的余角.
2、线面角向量法:
范围:
线面角等于直线的方向向量与平面的法向量所成角 的余角.
O
B
A
A
B
从一条直线出发的两个半平面所组成的图形叫做二面角。
这条直线叫做二面角的棱。
这两个半平面叫做二面角的面。
3
定义:
2、二面角
二面角的平面角必须满足:
3)角的边都要垂直于二面角的棱
1)角的顶点在棱上
2)角的两边分别在两个面内
以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角。
10
l
O
A
B
l
l
3、二面角的向量方法:
二面角的范围:
①向量法
注意法向量的方向:一进一出,二面角等于法向量夹角;
同进同出,二面角等于法向量夹角的补角
(六)、空间角的向量方法:
(七)空间“距离”问题
1. 空间两点之间的距离
根据两向量数量积的性质和坐标运算,
利用公式 或
(其中 ) ,可将两点距离问题
转化为求向量模长问题
2、E为平面α外一点,F为α内任意一 点, 为平面α的法向量,则点E到平面的距离为:
3、a,b是异面直线,E,F分别是直线a,b上的点, 是a,b公垂线的方向向量,则a,b间距离为
