2021-2022学年高一下学期物理人教版(2019)必修第二册6.3 向心加速度 课件(共33张PPT)
文档属性
| 名称 | 2021-2022学年高一下学期物理人教版(2019)必修第二册6.3 向心加速度 课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-12-06 15:53:40 | ||
图片预览











文档简介
(共33张PPT)
第六章 圆周运动
§6.3 向心加速度
CONTENTS
教学目标
01
知道匀速圆周运动中向心加速度大小的表达式,
理解向心加速度与半径的关系,并会用来进行简单的计算
03
能根据问题情境选择合适的向心加速度的表达式
02
了解分析匀速圆周运动速度变化量时用到的极限思想
01
教学重、难点
PART ONE
1.匀速圆周运动有什么特点?
2.向心力的来源是什么?
温故而知新
天宫二号空间实验室在轨飞行时,可认为它绕地球做匀速圆周运动。尽管线速度大小不变,但方向却时刻变化,因此,它运动的加速度一定不为 0。那么,该如何确定它在轨飞行时加速度的方向和大小呢?
脑洞大开
问题来了
做匀速圆周运动的物体,是否具有加速度?
问题来了
做匀速圆周运动的物体的加速度方向如何确定?依据是什么?
做匀速圆周运动的物体加速度指向圆心.这个加速度称为向心加速度.
根据牛顿第二定律,匀速圆周运动物体的加速度方向跟合外力的方向相同。
1
向心加速度
1.物理意义:
描述线速度方向变化的快慢
an
始终指向圆心
2.符号:
3.方向:
匀速圆周运动加速度的大小不变,方向时刻改变,所以匀速圆周运动不是匀变速运动,是变加速运动
4.说明:
问题来了
除了牛顿第二定律确定向心加速度的方向外,你还有什么方法可确定向心加速度的方向?
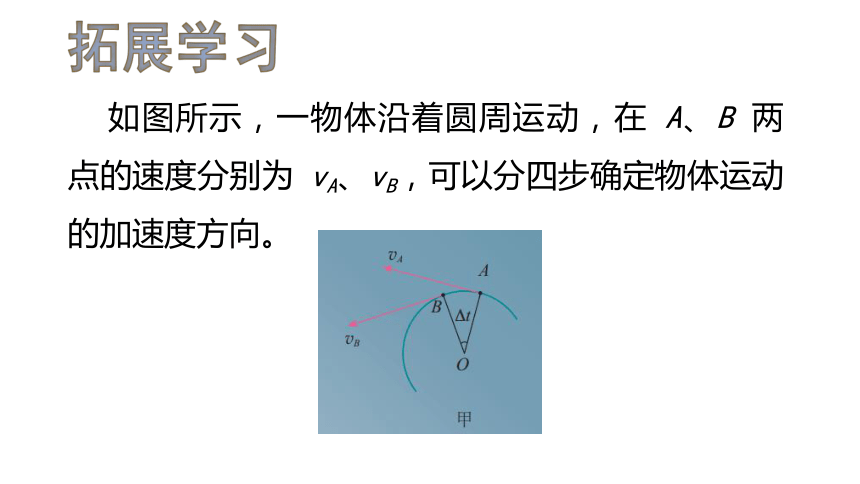
如图所示,一物体沿着圆周运动,在 A、B 两点的速度分别为 vA、vB,可以分四步确定物体运动的加速度方向。
拓展学习
第一步,根据曲线运动的速度方向沿着切线方向,画出物体经过 A、B 两点时的速度方向,分别用 vA、vB 表示,如图甲所示。
拓展学习
第二步,平移 vA 至 B 点,如图乙所示。
拓展学习
第三步,根据矢量运算法则,做出物体由 A 点到 B 点的速度变化量 Δv,其方向由 vA 的箭头位置指向 vB 的箭头位置,如图丙所示。由于物体做匀速圆周运动,vA、vB 的大小相等,所以,Δv与 vA、vB 构成等腰三角形。
拓展学习
第四步,假设由 A 点到 B 点的时间极短,在匀速圆周运动的速度大小一定的情况下,A 点到 B 点的距离将非常小,作出此时的 Δv,如图丁所示。
拓展学习
仔细观察图丁,可以发现,此时,Δv与vA、vB都几乎垂直,因此Δv的方向几乎沿着圆周的半径,指向圆心。由于加速度a与Δv的方向是一致的,所以从运动学角度分析也可以发现:物体做匀速圆周运动时的加速度指向圆心。
拓展学习
1.动力学原理:牛顿第二定律
2.运动学描述:加速度的定义式 (拓展学习)
两种探究方案:
2
向心加速度的大小
根据牛顿第二定律,结合上节学习的向心力表达式,推导向心加速度的表达式:
1. 用v 和 r 来表示向心加速度:
2. 用ω 和 r 来表示向心加速度:
3. 用 v 和ω 来表示向心加速度:
1.动力学原理:牛顿第二定律
2
向心加速度的大小
4. 用 T 和 r 来表示向心加速度:
5. 用 n ( f )和 r 来表示向心加速度:
根据牛顿第二定律,结合上节学习的向心力表达式,推导向心加速度的表达式:
1.动力学原理:牛顿第二定律
2
向心加速度的大小
思考讨论
1、当圆周运动的线速度一定时,向心加速度与半径r成反比;
2、当角速度ω一定时,向心加速度与半径r成正比。
PART ONE
01
思考讨论
PART ONE
他们两人的观点都不正确.
当v一定时,an与r成反比;当ω一定时,an与r成正比.
(an与r的关系图象如图所示)
拓展学习
向心加速度的推导过程
物体从A点经时间Δt沿圆周匀速率运动到B点,转过的角度为Δθ,如图所示,因为vA与OA垂直,vB与OB垂直,且vA=vB,OA=OB,所以△OAB与vA、vB、Δv组成的矢量三角形相似.
A
下列关于向心加速度的说法中,正确的是 ( )
向心加速度的方向始终与速度的方向垂直
向心加速度的方向保持不变
在匀速圆周运动中,向心加速度是恒定的
在匀速圆周运动中,向心加速度的大小不断变化
2、一物体在水平面内沿半径 R=20cm的圆形轨道做匀速圆周运动,线速度v =0.2m/s,则它的 向心加速度为______m/s2, 角速度为_____ rad/s,周期为_____s.
0.2
1
2π
3、关于北京和广州随地球自转的向心加速度,下列说法中正确的是 ( )
A、它们的方向都沿半径指向地心
B、它们的方向都平行于赤道平面指向地轴
C、北京的向心加速度比广州的向心加速度大
D、北京的向心加速度比广州的向心加速度小
BD
例4 、如图所示装置中,三个轮的半径分别为r、2r、4r,b点到圆心的距离为r,求图中a、b、c、d各点的加速度之比.
课堂小结
完成课后作业P34
01
学而不思则罔
思而不学则殆
PART ONE
第六章 圆周运动
§6.3 向心加速度
CONTENTS
教学目标
01
知道匀速圆周运动中向心加速度大小的表达式,
理解向心加速度与半径的关系,并会用来进行简单的计算
03
能根据问题情境选择合适的向心加速度的表达式
02
了解分析匀速圆周运动速度变化量时用到的极限思想
01
教学重、难点
PART ONE
1.匀速圆周运动有什么特点?
2.向心力的来源是什么?
温故而知新
天宫二号空间实验室在轨飞行时,可认为它绕地球做匀速圆周运动。尽管线速度大小不变,但方向却时刻变化,因此,它运动的加速度一定不为 0。那么,该如何确定它在轨飞行时加速度的方向和大小呢?
脑洞大开
问题来了
做匀速圆周运动的物体,是否具有加速度?
问题来了
做匀速圆周运动的物体的加速度方向如何确定?依据是什么?
做匀速圆周运动的物体加速度指向圆心.这个加速度称为向心加速度.
根据牛顿第二定律,匀速圆周运动物体的加速度方向跟合外力的方向相同。
1
向心加速度
1.物理意义:
描述线速度方向变化的快慢
an
始终指向圆心
2.符号:
3.方向:
匀速圆周运动加速度的大小不变,方向时刻改变,所以匀速圆周运动不是匀变速运动,是变加速运动
4.说明:
问题来了
除了牛顿第二定律确定向心加速度的方向外,你还有什么方法可确定向心加速度的方向?
如图所示,一物体沿着圆周运动,在 A、B 两点的速度分别为 vA、vB,可以分四步确定物体运动的加速度方向。
拓展学习
第一步,根据曲线运动的速度方向沿着切线方向,画出物体经过 A、B 两点时的速度方向,分别用 vA、vB 表示,如图甲所示。
拓展学习
第二步,平移 vA 至 B 点,如图乙所示。
拓展学习
第三步,根据矢量运算法则,做出物体由 A 点到 B 点的速度变化量 Δv,其方向由 vA 的箭头位置指向 vB 的箭头位置,如图丙所示。由于物体做匀速圆周运动,vA、vB 的大小相等,所以,Δv与 vA、vB 构成等腰三角形。
拓展学习
第四步,假设由 A 点到 B 点的时间极短,在匀速圆周运动的速度大小一定的情况下,A 点到 B 点的距离将非常小,作出此时的 Δv,如图丁所示。
拓展学习
仔细观察图丁,可以发现,此时,Δv与vA、vB都几乎垂直,因此Δv的方向几乎沿着圆周的半径,指向圆心。由于加速度a与Δv的方向是一致的,所以从运动学角度分析也可以发现:物体做匀速圆周运动时的加速度指向圆心。
拓展学习
1.动力学原理:牛顿第二定律
2.运动学描述:加速度的定义式 (拓展学习)
两种探究方案:
2
向心加速度的大小
根据牛顿第二定律,结合上节学习的向心力表达式,推导向心加速度的表达式:
1. 用v 和 r 来表示向心加速度:
2. 用ω 和 r 来表示向心加速度:
3. 用 v 和ω 来表示向心加速度:
1.动力学原理:牛顿第二定律
2
向心加速度的大小
4. 用 T 和 r 来表示向心加速度:
5. 用 n ( f )和 r 来表示向心加速度:
根据牛顿第二定律,结合上节学习的向心力表达式,推导向心加速度的表达式:
1.动力学原理:牛顿第二定律
2
向心加速度的大小
思考讨论
1、当圆周运动的线速度一定时,向心加速度与半径r成反比;
2、当角速度ω一定时,向心加速度与半径r成正比。
PART ONE
01
思考讨论
PART ONE
他们两人的观点都不正确.
当v一定时,an与r成反比;当ω一定时,an与r成正比.
(an与r的关系图象如图所示)
拓展学习
向心加速度的推导过程
物体从A点经时间Δt沿圆周匀速率运动到B点,转过的角度为Δθ,如图所示,因为vA与OA垂直,vB与OB垂直,且vA=vB,OA=OB,所以△OAB与vA、vB、Δv组成的矢量三角形相似.
A
下列关于向心加速度的说法中,正确的是 ( )
向心加速度的方向始终与速度的方向垂直
向心加速度的方向保持不变
在匀速圆周运动中,向心加速度是恒定的
在匀速圆周运动中,向心加速度的大小不断变化
2、一物体在水平面内沿半径 R=20cm的圆形轨道做匀速圆周运动,线速度v =0.2m/s,则它的 向心加速度为______m/s2, 角速度为_____ rad/s,周期为_____s.
0.2
1
2π
3、关于北京和广州随地球自转的向心加速度,下列说法中正确的是 ( )
A、它们的方向都沿半径指向地心
B、它们的方向都平行于赤道平面指向地轴
C、北京的向心加速度比广州的向心加速度大
D、北京的向心加速度比广州的向心加速度小
BD
例4 、如图所示装置中,三个轮的半径分别为r、2r、4r,b点到圆心的距离为r,求图中a、b、c、d各点的加速度之比.
课堂小结
完成课后作业P34
01
学而不思则罔
思而不学则殆
PART ONE
