2021-2022学年高二上学期数学 上教版(2020)必修第三册12.4 随机事件的独立性 课件(共17张PPT)
文档属性
| 名称 | 2021-2022学年高二上学期数学 上教版(2020)必修第三册12.4 随机事件的独立性 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 162.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 上教版(2020) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 19:26:01 | ||
图片预览






文档简介
(共17张PPT)
12.4 随机事件的独立性
引入
伯努利大数定律
独立地重复一个伯努利试验n次,当n很大时,频率 逼近概率
那么,什么样的事件才可称为是“相互独立”的?以及,相互独立事件同时发生的概率可以如何计算?
情境创设
利用古典概型计算下列问题,观察 P(A)P(B) 与 P(A∩B) 的关系
并从直观上判断各个问题中的事件是否互相影响?(注:H/T分别表示硬币的正反面)
问题1-1设随机试验E为“抛甲、乙两枚硬币,观察正反面出现的情况”。设事件A为“甲币出现H”,事件B为“乙币出现H”. 试计算P(A)、P(B)、P(A∩B) 解: 问题1-2 考虑随机事件:抛掷一枚质地均匀的硬币,抛掷一颗质量均匀的骰子。设事件A为“硬币出现H”,事件B为“骰子出现3”. 试计算P(A)、P(B)、P(A∩B)
解:
对上述问题的思考
对问题1中的两个问题,我们容易从直观上判断事件A、B的发生互不影响,或者说,事件A、B相互独立,且此时
这给我们提供了计算P(A∩B)的一种更为简便的方法,使得我们不需要列举等可能样本空间就可以快速的计算出P(A∩B)
概念形成-事件的独立性
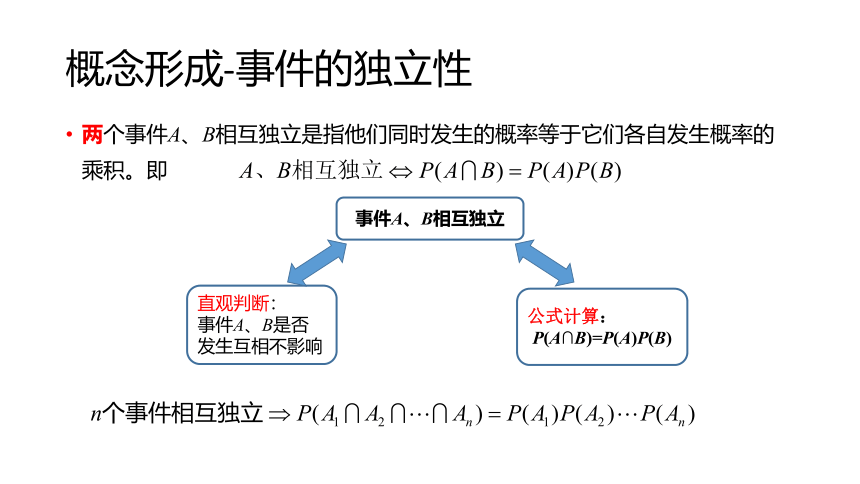
两个事件A、B相互独立是指他们同时发生的概率等于它们各自发生概率的乘积。即
直观判断:
事件A、B是否发生互相不影响
事件A、B相互独立
公式计算:
P(A∩B)=P(A)P(B)
事件独立性(引例)
引例:甲袋中有2个红球1个黑球,乙袋中有1个红球2个黑球,记事件
A:从甲袋中任取一球结果是黑球;
B:从乙袋中任取一球结果是红球;
试判断:A与B 是否相互独立?
典型例题1
证明:如果A与B两个事件相互独立,那么下列事件也相互独立:
证明:因为
而
所以
因此,
独立事件的性质
定义辨析
1、若P(A)≠ 0,P(B)≠ 0,则A、B相互独立与A、B互斥不能同时成立
2、必然事件Ω和不可能事件 与任何不确定事件A都是相互独立的。
典型例题2
依次抛掷10枚硬币(抛掷过程互不影响),观察朝上的面。求
(1)都是正面朝上的概率;
(2)只有第一枚反面朝上的概率;
(2)恰有1枚反面朝上的概率
直观判断独立性并计算
课堂练习
1、掷两颗骰子,使用独立性求:
(1)它们的点数都是偶数的概率;
(2)它们的点数是一奇一偶的概率
2、已知事件A与B相互独立,如果P(A)=0.3,P(B)=0.6,那么
P(A∩ B)=________,
典型例题3(弱者的机会)
两个人比赛,对于弱者(赢的概率较小者)来说,一局定胜负和三局两胜比较,哪个更有利?(假设弱者每局赢的概率均相同,各局互不影响且无和棋)
注:“三局两胜”是常见的比赛模式,指先赢得两局者为胜,最多三局结束。
解:设A、B两人比赛。A为弱者,每一局赢的概率为p
思考题4(领先一局带来的收益)
A、B两人下棋,每局两人获胜的可能性一样,每局之间互不影响且无和棋。某一天两人要进行一场三局两胜的比赛,最终胜者赢得1000英镑的奖金。第一局 比赛A胜,后因为其他要事而中止比赛。问:怎么分这1000英镑的奖金才算公平?
怎么分才公平?帕斯卡和费马认为应该依据在现有状态下,按两人最终获胜的可能性大小来分。
记A表示事件“A最终胜”;
Ai表示事件“第i局A胜”
则
又因每局相互独立,且
所以
因此,A、B两人应该按3:1来分奖金。
解法3:构造随机事件的等可能样本空间
Ω={AA,AB,BA,BB}
A最终获胜的概率:
B最终获胜的概率:
因此,A、B两人应该按3:1来分奖金
对题4的再思考1
将上述奖金分配问题的三局两胜规则改为五局三胜,试问在比分是2:1的情况下,怎么分配奖金公平?
对题4的再思考2
将上述奖金分配问题的三局两胜规则改为五局三胜,试问在比分是1:0的情况下,怎么分配奖金公平?
小结评价
随机事件独立性的定义
随机事件独立性的判断
随机事件独立性的应用
你对随机事件独立性的理解程度:
A 理解并熟练掌握 B 会做题 C 理解但不熟练
D还有点不会 E不懂 F其他___
直观判断:
事件A、B是否发生互相不影响
事件A、B相互独立
公式计算:
P(A∩B)=P(A)P(B)
课后作业
学生自评:
练习12.4(2)T1,2,3
校本练习册:习题12.4 A组 T1,3;B组 T1,3
12.4 随机事件的独立性
引入
伯努利大数定律
独立地重复一个伯努利试验n次,当n很大时,频率 逼近概率
那么,什么样的事件才可称为是“相互独立”的?以及,相互独立事件同时发生的概率可以如何计算?
情境创设
利用古典概型计算下列问题,观察 P(A)P(B) 与 P(A∩B) 的关系
并从直观上判断各个问题中的事件是否互相影响?(注:H/T分别表示硬币的正反面)
问题1-1设随机试验E为“抛甲、乙两枚硬币,观察正反面出现的情况”。设事件A为“甲币出现H”,事件B为“乙币出现H”. 试计算P(A)、P(B)、P(A∩B) 解: 问题1-2 考虑随机事件:抛掷一枚质地均匀的硬币,抛掷一颗质量均匀的骰子。设事件A为“硬币出现H”,事件B为“骰子出现3”. 试计算P(A)、P(B)、P(A∩B)
解:
对上述问题的思考
对问题1中的两个问题,我们容易从直观上判断事件A、B的发生互不影响,或者说,事件A、B相互独立,且此时
这给我们提供了计算P(A∩B)的一种更为简便的方法,使得我们不需要列举等可能样本空间就可以快速的计算出P(A∩B)
概念形成-事件的独立性
两个事件A、B相互独立是指他们同时发生的概率等于它们各自发生概率的乘积。即
直观判断:
事件A、B是否发生互相不影响
事件A、B相互独立
公式计算:
P(A∩B)=P(A)P(B)
事件独立性(引例)
引例:甲袋中有2个红球1个黑球,乙袋中有1个红球2个黑球,记事件
A:从甲袋中任取一球结果是黑球;
B:从乙袋中任取一球结果是红球;
试判断:A与B 是否相互独立?
典型例题1
证明:如果A与B两个事件相互独立,那么下列事件也相互独立:
证明:因为
而
所以
因此,
独立事件的性质
定义辨析
1、若P(A)≠ 0,P(B)≠ 0,则A、B相互独立与A、B互斥不能同时成立
2、必然事件Ω和不可能事件 与任何不确定事件A都是相互独立的。
典型例题2
依次抛掷10枚硬币(抛掷过程互不影响),观察朝上的面。求
(1)都是正面朝上的概率;
(2)只有第一枚反面朝上的概率;
(2)恰有1枚反面朝上的概率
直观判断独立性并计算
课堂练习
1、掷两颗骰子,使用独立性求:
(1)它们的点数都是偶数的概率;
(2)它们的点数是一奇一偶的概率
2、已知事件A与B相互独立,如果P(A)=0.3,P(B)=0.6,那么
P(A∩ B)=________,
典型例题3(弱者的机会)
两个人比赛,对于弱者(赢的概率较小者)来说,一局定胜负和三局两胜比较,哪个更有利?(假设弱者每局赢的概率均相同,各局互不影响且无和棋)
注:“三局两胜”是常见的比赛模式,指先赢得两局者为胜,最多三局结束。
解:设A、B两人比赛。A为弱者,每一局赢的概率为p
思考题4(领先一局带来的收益)
A、B两人下棋,每局两人获胜的可能性一样,每局之间互不影响且无和棋。某一天两人要进行一场三局两胜的比赛,最终胜者赢得1000英镑的奖金。第一局 比赛A胜,后因为其他要事而中止比赛。问:怎么分这1000英镑的奖金才算公平?
怎么分才公平?帕斯卡和费马认为应该依据在现有状态下,按两人最终获胜的可能性大小来分。
记A表示事件“A最终胜”;
Ai表示事件“第i局A胜”
则
又因每局相互独立,且
所以
因此,A、B两人应该按3:1来分奖金。
解法3:构造随机事件的等可能样本空间
Ω={AA,AB,BA,BB}
A最终获胜的概率:
B最终获胜的概率:
因此,A、B两人应该按3:1来分奖金
对题4的再思考1
将上述奖金分配问题的三局两胜规则改为五局三胜,试问在比分是2:1的情况下,怎么分配奖金公平?
对题4的再思考2
将上述奖金分配问题的三局两胜规则改为五局三胜,试问在比分是1:0的情况下,怎么分配奖金公平?
小结评价
随机事件独立性的定义
随机事件独立性的判断
随机事件独立性的应用
你对随机事件独立性的理解程度:
A 理解并熟练掌握 B 会做题 C 理解但不熟练
D还有点不会 E不懂 F其他___
直观判断:
事件A、B是否发生互相不影响
事件A、B相互独立
公式计算:
P(A∩B)=P(A)P(B)
课后作业
学生自评:
练习12.4(2)T1,2,3
校本练习册:习题12.4 A组 T1,3;B组 T1,3
同课章节目录
