小学数学青岛版(六三制)四年级下第三单元 快乐农场——运算律回顾整理课件(30张PPT)
文档属性
| 名称 | 小学数学青岛版(六三制)四年级下第三单元 快乐农场——运算律回顾整理课件(30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 17:33:39 | ||
图片预览










文档简介
(共30张PPT)
回顾整理
青岛版数学四年级(下)
三 快乐农场
——运算律
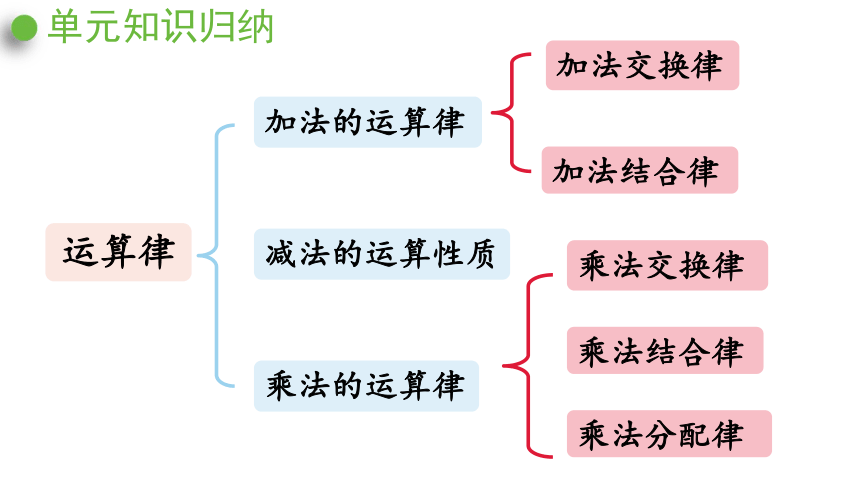
单元知识归纳
运算律
加法的运算律
加法结合律
加法交换律
乘法交换律
乘法分配律
减法的运算性质
乘法的运算律
乘法结合律
接下来我们一起回顾一下吧!
经过这一单元的学习,你有哪些收获?
我会运用运算律使计算简便。
我学会了加法运算律和乘法运算律
……
加法结合律
三个数相加,先把前两个数相加再加第三个数,或者先把后两个数相加再加第一个数,和不变。这就叫加法结合律。用字母表示为( a + b )+c = a + ( b + c )。
加法交换律
两个数相加,交换加数的位置,他们的和不变,这个规律叫作加法交换律。用字母表示为:a + b = b + a。
加法运算律的运用
1.在一个加法算式中,当某些加数可以凑成整十、整百……的数时,运用加法运算律使这几个加数先相加,使计算简便。
2.运用加法交换律还可以进行验算。
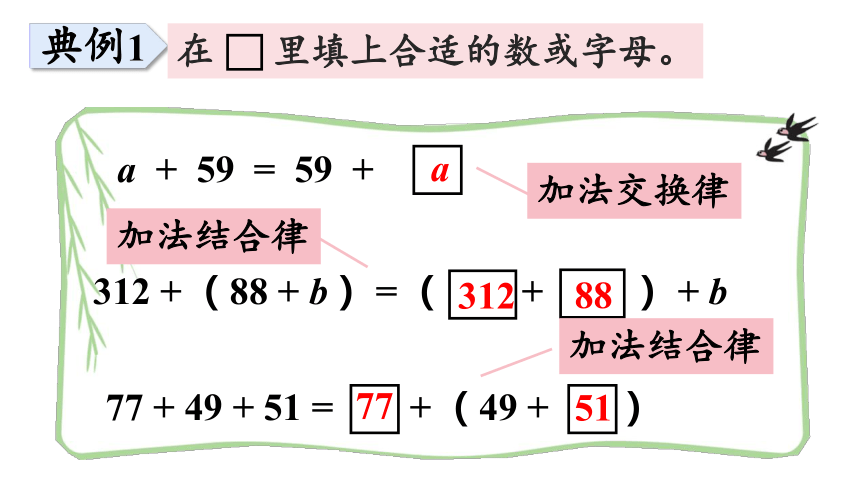
典例1
在 里填上合适的数或字母。
a + 59 = 59 +
312 +( 88 + b )=( + )+ b
77 + 49 + 51 = +( 49 + )
a
312
88
77
51
加法交换律
加法结合律
加法结合律
典例2
用简便方法计算。
(1) 98 + 198 + 1998 + 2 × 3
(2)9 + 99 + 999 + 9999
=100-2
=200-2
=2000-2
=2+2+2
(1) 98 + 198 + 1998 + 2 × 3
= (100 – 2)+(200 – 2)+(2000 – 2)+2+2+2
= 100 – 2 + 200 – 2 + 2000 – 2+2+2+2
= 100 + 200 + 2000
= 2300
=100-2
=200-2
=2000-2
=2+2+2
典例2
用简便方法计算。
(1) 98 + 198 + 1998 + 2 × 3
(2)9 + 99 + 999 + 9999
=100-2
=200-2
=2000-2
=2+2+2
=10-1
=100-1
=1000-1
=10000-1
(2)9 + 99 + 999 + 9999
=10-1
=100-1
=1000-1
=10000-1
= (10 – 1)+(100 – 1)+(1000 – 1)+(10000 – 1)
= 10 – 1+100 – 1+1000 – 1+10000 – 1
= 10 + 100 +1000 + 10000 – 1– 1– 1
= 11110 – 1– 1– 1
= 10007
减法的运算性质
一个数连续减去两个数,等于从这个数里减去这两个数的和,这就是减法的运算性质。用字母表示为:
a-b-c = a -(b + c)。
典例3
用简便方法计算。
(1)629 – 135 – 65
(2)9803 –( 190 + 803)
135+65=200
= 629 –( 135 + 65 )
= 629 – 200
= 429
典例3
用简便方法计算。
(2)9803 –( 190 + 803)
9803-803=9000
= 9803 – 190 – 803
= 9803 – 803 – 190
= 9000 – 190
= 8810
乘法结合律
三个数相乘,先把前两个数相乘,再同第三个数相乘,或者先把后两个数相乘,再同第一个数相乘,它们的积不变。这就叫乘法结合律。用字母表示为:
( a · b ) · c = a ·( b · c )
乘法交换律
两个数相乘,交换因数的位置,它们的积不变,这个规律叫作乘法交换律。用字母表示为:
a · b = b · a
乘法分配律
两个数的和乘一个数,可以把它们分别乘这个数,再把两个积相加,结果不变。这叫作乘法分配律。用字母表示为:
( a + b )· c = a · c + b · c
两数之差乘另一个数同样适用
乘法运算律的运用
1.在一个乘法算式中,当某些因数可以凑成整十、整百……的数时,运用乘法运算律使这几个因数先相乘,使计算简便。
2.运用乘法交换律还可以进行验算。
典例4
在 里填上合适的数或字母。
32 × b = b ×
c ×( × )= c × 8 × 125
a ×3 +17 × a = ×( 3 + )
32
125
8
a
17
乘法交换律
乘法结合律
乘法分配律
典例5
用简便方法计算。
(1) 20× 178 × 5
(2)168×15-68×15
= 178 ×( 20 × 5)
= 178 × 100
= 17800
20×5=100
典例5
用简便方法计算。
(2)168 × 15 - 68 × 15
有相同因数15
168 – 68 = 100
= ( 168 - 68 ) × 15
= 100 × 15
= 1500
工程队 每月的绿化面积(平方米)
环宇 366
志远 476
鹏飞 524
(1)中心广场进行绿化养护,平均每月花费2万元,5年共需绿化养护费多少万元?
2×12×5=2×5×12=120(万元)
1
一年花费(2×12)万元
(教材第31页“我学会了吗?”)
(2)花园小区的绿化任务由环宇、志远、鹏飞三个工程队共同承担,计划3个月完成。
①三个工程队每个月一共要绿化多少平方米?
366 + 476 + 524
= 366 +( 476 + 524)
= 1366(平方米)
工程队 每月的绿化面积(平方米)
环宇 366
志远 476
鹏飞 524
(教材第31页“我学会了吗?”)
②志远队和鹏飞队3个月一共要绿化多少平方米?
(2)花园小区的绿化任务由环宇、志远、鹏飞三个工程队共同承担,计划3个月完成。
(476 + 524) × 3
= 1000×3
= 3000(平方米)
工程队 每月的绿化面积(平方米)
环宇 366
志远 476
鹏飞 524
(教材第31页“我学会了吗?”)
(1)41 × 18 + 59 × 18 =(41+59)×( ),运用了( )律。
(2)125+147+175=147+(125+175)这是运用了( )律和( )律。
18
乘法分配
加法交换
加法结合
填一填。
2
相同因数
运算顺序和因数位置都发生变化
(3)从植物园到车站25千米,王师傅每天开车行驶4个来回,王师傅每天行驶( )千米。
一个来回是2个“25千米”
4×2×25=200(千米)
200
填一填。
2
两个加数调换位置,和不变。( )
2. a ·( b + c )= a · b + b · c。( )
3. 56×18+43×18+18的简便算法是(56+43+1)×18。( )
√
×
√
加法交换律
= a · b + a · c
乘法分配律
判断。
3
149+128+151+72 25×7×4
=(149+151)+(128+72)
= 300+200
= 500
= 7×(25×4)
= 7×100
= 700
简便计算。
4
凑整
凑整
凑整
= 142×(100 – 1)
= 142×100 – 142 ×1
= 14200 – 142
= 333×3×11+333×67
= 333×(3×11+67)
142×99 999×11+333×67
99=100-1
= 14058
999=333×3
= 333×(33+67)
= 333×100
= 33300
简便计算。
4
142×(42+58)
=142×100
=14200(平方米)
答:两个班的同学这一天捡的废旧电池一共能减少14200平方米的土壤污染。
一节废旧电池能造成周围约145平方分米的土壤污染。四(1)班同学在环保活动中一天捡了58节废旧电池,四(2)班同学一天捡了42节废旧电池。两个班的同学这一天捡的废旧电池一共能减少多少土壤污染?
5
回顾整理
青岛版数学四年级(下)
三 快乐农场
——运算律
单元知识归纳
运算律
加法的运算律
加法结合律
加法交换律
乘法交换律
乘法分配律
减法的运算性质
乘法的运算律
乘法结合律
接下来我们一起回顾一下吧!
经过这一单元的学习,你有哪些收获?
我会运用运算律使计算简便。
我学会了加法运算律和乘法运算律
……
加法结合律
三个数相加,先把前两个数相加再加第三个数,或者先把后两个数相加再加第一个数,和不变。这就叫加法结合律。用字母表示为( a + b )+c = a + ( b + c )。
加法交换律
两个数相加,交换加数的位置,他们的和不变,这个规律叫作加法交换律。用字母表示为:a + b = b + a。
加法运算律的运用
1.在一个加法算式中,当某些加数可以凑成整十、整百……的数时,运用加法运算律使这几个加数先相加,使计算简便。
2.运用加法交换律还可以进行验算。
典例1
在 里填上合适的数或字母。
a + 59 = 59 +
312 +( 88 + b )=( + )+ b
77 + 49 + 51 = +( 49 + )
a
312
88
77
51
加法交换律
加法结合律
加法结合律
典例2
用简便方法计算。
(1) 98 + 198 + 1998 + 2 × 3
(2)9 + 99 + 999 + 9999
=100-2
=200-2
=2000-2
=2+2+2
(1) 98 + 198 + 1998 + 2 × 3
= (100 – 2)+(200 – 2)+(2000 – 2)+2+2+2
= 100 – 2 + 200 – 2 + 2000 – 2+2+2+2
= 100 + 200 + 2000
= 2300
=100-2
=200-2
=2000-2
=2+2+2
典例2
用简便方法计算。
(1) 98 + 198 + 1998 + 2 × 3
(2)9 + 99 + 999 + 9999
=100-2
=200-2
=2000-2
=2+2+2
=10-1
=100-1
=1000-1
=10000-1
(2)9 + 99 + 999 + 9999
=10-1
=100-1
=1000-1
=10000-1
= (10 – 1)+(100 – 1)+(1000 – 1)+(10000 – 1)
= 10 – 1+100 – 1+1000 – 1+10000 – 1
= 10 + 100 +1000 + 10000 – 1– 1– 1
= 11110 – 1– 1– 1
= 10007
减法的运算性质
一个数连续减去两个数,等于从这个数里减去这两个数的和,这就是减法的运算性质。用字母表示为:
a-b-c = a -(b + c)。
典例3
用简便方法计算。
(1)629 – 135 – 65
(2)9803 –( 190 + 803)
135+65=200
= 629 –( 135 + 65 )
= 629 – 200
= 429
典例3
用简便方法计算。
(2)9803 –( 190 + 803)
9803-803=9000
= 9803 – 190 – 803
= 9803 – 803 – 190
= 9000 – 190
= 8810
乘法结合律
三个数相乘,先把前两个数相乘,再同第三个数相乘,或者先把后两个数相乘,再同第一个数相乘,它们的积不变。这就叫乘法结合律。用字母表示为:
( a · b ) · c = a ·( b · c )
乘法交换律
两个数相乘,交换因数的位置,它们的积不变,这个规律叫作乘法交换律。用字母表示为:
a · b = b · a
乘法分配律
两个数的和乘一个数,可以把它们分别乘这个数,再把两个积相加,结果不变。这叫作乘法分配律。用字母表示为:
( a + b )· c = a · c + b · c
两数之差乘另一个数同样适用
乘法运算律的运用
1.在一个乘法算式中,当某些因数可以凑成整十、整百……的数时,运用乘法运算律使这几个因数先相乘,使计算简便。
2.运用乘法交换律还可以进行验算。
典例4
在 里填上合适的数或字母。
32 × b = b ×
c ×( × )= c × 8 × 125
a ×3 +17 × a = ×( 3 + )
32
125
8
a
17
乘法交换律
乘法结合律
乘法分配律
典例5
用简便方法计算。
(1) 20× 178 × 5
(2)168×15-68×15
= 178 ×( 20 × 5)
= 178 × 100
= 17800
20×5=100
典例5
用简便方法计算。
(2)168 × 15 - 68 × 15
有相同因数15
168 – 68 = 100
= ( 168 - 68 ) × 15
= 100 × 15
= 1500
工程队 每月的绿化面积(平方米)
环宇 366
志远 476
鹏飞 524
(1)中心广场进行绿化养护,平均每月花费2万元,5年共需绿化养护费多少万元?
2×12×5=2×5×12=120(万元)
1
一年花费(2×12)万元
(教材第31页“我学会了吗?”)
(2)花园小区的绿化任务由环宇、志远、鹏飞三个工程队共同承担,计划3个月完成。
①三个工程队每个月一共要绿化多少平方米?
366 + 476 + 524
= 366 +( 476 + 524)
= 1366(平方米)
工程队 每月的绿化面积(平方米)
环宇 366
志远 476
鹏飞 524
(教材第31页“我学会了吗?”)
②志远队和鹏飞队3个月一共要绿化多少平方米?
(2)花园小区的绿化任务由环宇、志远、鹏飞三个工程队共同承担,计划3个月完成。
(476 + 524) × 3
= 1000×3
= 3000(平方米)
工程队 每月的绿化面积(平方米)
环宇 366
志远 476
鹏飞 524
(教材第31页“我学会了吗?”)
(1)41 × 18 + 59 × 18 =(41+59)×( ),运用了( )律。
(2)125+147+175=147+(125+175)这是运用了( )律和( )律。
18
乘法分配
加法交换
加法结合
填一填。
2
相同因数
运算顺序和因数位置都发生变化
(3)从植物园到车站25千米,王师傅每天开车行驶4个来回,王师傅每天行驶( )千米。
一个来回是2个“25千米”
4×2×25=200(千米)
200
填一填。
2
两个加数调换位置,和不变。( )
2. a ·( b + c )= a · b + b · c。( )
3. 56×18+43×18+18的简便算法是(56+43+1)×18。( )
√
×
√
加法交换律
= a · b + a · c
乘法分配律
判断。
3
149+128+151+72 25×7×4
=(149+151)+(128+72)
= 300+200
= 500
= 7×(25×4)
= 7×100
= 700
简便计算。
4
凑整
凑整
凑整
= 142×(100 – 1)
= 142×100 – 142 ×1
= 14200 – 142
= 333×3×11+333×67
= 333×(3×11+67)
142×99 999×11+333×67
99=100-1
= 14058
999=333×3
= 333×(33+67)
= 333×100
= 33300
简便计算。
4
142×(42+58)
=142×100
=14200(平方米)
答:两个班的同学这一天捡的废旧电池一共能减少14200平方米的土壤污染。
一节废旧电池能造成周围约145平方分米的土壤污染。四(1)班同学在环保活动中一天捡了58节废旧电池,四(2)班同学一天捡了42节废旧电池。两个班的同学这一天捡的废旧电池一共能减少多少土壤污染?
5
