7.3平行线的判定 课件(共12张PPT)
文档属性
| 名称 | 7.3平行线的判定 课件(共12张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-09 11:42:23 | ||
图片预览





文档简介
(共12张PPT)
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8
0 1 2 3 4 5
0 1 2 3 4 5
北师大版 八年级 上册(第七章)
1.公理:
人们在长期实践中总结出来的,并作为判定其他命题真假的根据.
2.定理:
用推理的方法得到的真命题.
3.证明:
除公理外,一个命题的正确性需要经过推理,才能作出判断,这个推理的过程叫做证明.
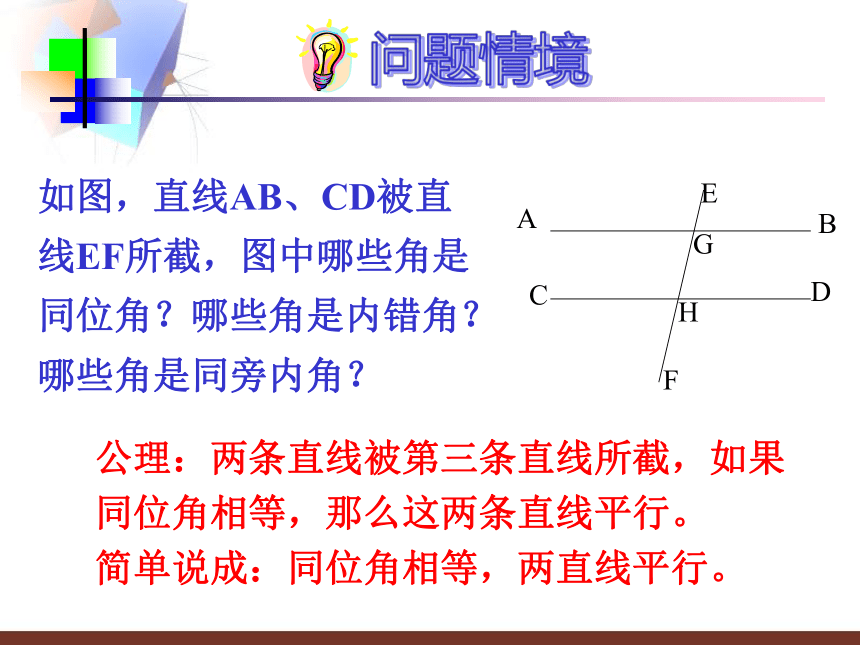
公理:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
简单说成:同位角相等,两直线平行。
如图,直线AB、CD被直线EF所截,图中哪些角是同位角?哪些角是内错角?哪些角是同旁内角?
A
B
C
D
E
F
G
H
你认为“两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行”这个命题正确吗?说明理由。
已知:如图,∠1和 ∠2是直线a、 b被直线c截出的同旁内角,且∠1与 ∠2互补。求证:a ∥b .
证明:∵ ∠1与 ∠2互补(已知),
∴ ∠1+ ∠2= 180 °(互补的定义)
∴ ∠1= 180 °- ∠2(等式的性质)
∵ ∠3+ ∠2= 180 °(1平角= 180 °)
∴ ∠3= 180 °- ∠2(等式的性质)
∴ ∠1= ∠3(等量代换)
∴ a ∥b(同位角相等,两直线平行)
1
3
a
b
c
2
证明一个命题的一般步骤:
(1)弄清题设和结论; (2)根据题意画出相应的图形;
(3)根据题设和结论写出已知,求证; (4)分析证明思路,写出证明过程.
小明用下面的方法 作出了平行线,你认为他的作法吗?为什么?
定理 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。简单说成:内错角相等,两条直线平行。
已知:如图,∠1和 ∠2是直线a、 b被直线c截出的内错角,且∠1= ∠2。求证:a ∥b .
证明: ∵ ∠1= ∠2(已知)
∠1+ ∠3=180 ° (1平角=180 ° )
∴ ∠2+ ∠3=180 ° (等量代换)
∴ ∠2与 ∠3互补(互补的定义)
∴ a ∥b(同旁内角互补,两直线平行)
1
2
3
借助“同位角相等,两条直线平行”这一公理,你还能证明哪些熟悉的结论?
练习:1 、蜂房的底部由三个全等的四边形围成的,每个四边形的形状如图所示,其中∠α=109°28′, ∠β=70°32′。试确定这三个四边形的形状,并说明你的理由。
A
B
C
D
解:
∵∠A+∠D=180o
∴ AB∥CD
∴ ABCD为平行四边形
同理可证:AD∥BC
即所求三个四边形为平行四边形
2、证明:对顶角相等。
已知:如图,直线AB、CD相交于点O, ∠1和∠2是对顶角,
求证: ∠1= ∠2。
证明:∵ ∠1+∠AOC=180 °(1平角=180 ° ),
∠2+∠AOC=180 ° ( 1平角=180 ° ),
∴ ∠1= ∠2(同角的补角相等)。
EF
内错角相等,两直线平行
BC
同旁内角互补,两直线平行
AD
BC
平行于同一条直线的两条直线互相平行
3、完成下列推理,并在括号中写出相应的根据。
∴ ∥ 。
(1)如图甲所示
∵ ∠ADE= ∠DEF(已知)
∴ AD ∥ ( )
又∵ ∠EFC+ ∠C= 180 °
∴ EF ∥ ( )
( )
( )
(2)如图乙所示
∵ AC ⊥ AB,BF ⊥ AB ( )
∴ ∠ CAB = ∠ ABF=90 ° ( )
∵ ∠ CAD= ∠ EBF=30 ° ( )
∴ = ( )
∴ ∥ 。
等式的性质
垂直的性质
BE
∠EBA
内错角相等,两直线平行
∠ABD
AD
已知
已知
继 续
已知:如图直线a、 b被直线c所截,且∠1+∠2=180 °
求证: a ∥b。
你有几种证明方法?
3
4
方法1:
∵ ∠ 1 + ∠ 2 = 180 °
∴ ∠ 2 = ∠ 4
∠ 1 + ∠ 4 = 180 °
∴ a ∥b
(同位角相等,两直线平行)
方法2:
∵ ∠ 1 + ∠ 2 = 180 °
∴ ∠ 2 + ∠ 3= 180 °
∠ 1 = ∠ 3
∴ a ∥b
(同旁内角互补,两直线平行)
小结
证明一个命题的一般步骤:
(1)弄清题设和结论;
(2)根据题意画出相应的图形;
(3)根据题设和结论写出已知,求证;
(4)分析证明思路,写出证明过程.
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8
0 1 2 3 4 5
0 1 2 3 4 5
北师大版 八年级 上册(第七章)
1.公理:
人们在长期实践中总结出来的,并作为判定其他命题真假的根据.
2.定理:
用推理的方法得到的真命题.
3.证明:
除公理外,一个命题的正确性需要经过推理,才能作出判断,这个推理的过程叫做证明.
公理:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
简单说成:同位角相等,两直线平行。
如图,直线AB、CD被直线EF所截,图中哪些角是同位角?哪些角是内错角?哪些角是同旁内角?
A
B
C
D
E
F
G
H
你认为“两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行”这个命题正确吗?说明理由。
已知:如图,∠1和 ∠2是直线a、 b被直线c截出的同旁内角,且∠1与 ∠2互补。求证:a ∥b .
证明:∵ ∠1与 ∠2互补(已知),
∴ ∠1+ ∠2= 180 °(互补的定义)
∴ ∠1= 180 °- ∠2(等式的性质)
∵ ∠3+ ∠2= 180 °(1平角= 180 °)
∴ ∠3= 180 °- ∠2(等式的性质)
∴ ∠1= ∠3(等量代换)
∴ a ∥b(同位角相等,两直线平行)
1
3
a
b
c
2
证明一个命题的一般步骤:
(1)弄清题设和结论; (2)根据题意画出相应的图形;
(3)根据题设和结论写出已知,求证; (4)分析证明思路,写出证明过程.
小明用下面的方法 作出了平行线,你认为他的作法吗?为什么?
定理 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。简单说成:内错角相等,两条直线平行。
已知:如图,∠1和 ∠2是直线a、 b被直线c截出的内错角,且∠1= ∠2。求证:a ∥b .
证明: ∵ ∠1= ∠2(已知)
∠1+ ∠3=180 ° (1平角=180 ° )
∴ ∠2+ ∠3=180 ° (等量代换)
∴ ∠2与 ∠3互补(互补的定义)
∴ a ∥b(同旁内角互补,两直线平行)
1
2
3
借助“同位角相等,两条直线平行”这一公理,你还能证明哪些熟悉的结论?
练习:1 、蜂房的底部由三个全等的四边形围成的,每个四边形的形状如图所示,其中∠α=109°28′, ∠β=70°32′。试确定这三个四边形的形状,并说明你的理由。
A
B
C
D
解:
∵∠A+∠D=180o
∴ AB∥CD
∴ ABCD为平行四边形
同理可证:AD∥BC
即所求三个四边形为平行四边形
2、证明:对顶角相等。
已知:如图,直线AB、CD相交于点O, ∠1和∠2是对顶角,
求证: ∠1= ∠2。
证明:∵ ∠1+∠AOC=180 °(1平角=180 ° ),
∠2+∠AOC=180 ° ( 1平角=180 ° ),
∴ ∠1= ∠2(同角的补角相等)。
EF
内错角相等,两直线平行
BC
同旁内角互补,两直线平行
AD
BC
平行于同一条直线的两条直线互相平行
3、完成下列推理,并在括号中写出相应的根据。
∴ ∥ 。
(1)如图甲所示
∵ ∠ADE= ∠DEF(已知)
∴ AD ∥ ( )
又∵ ∠EFC+ ∠C= 180 °
∴ EF ∥ ( )
( )
( )
(2)如图乙所示
∵ AC ⊥ AB,BF ⊥ AB ( )
∴ ∠ CAB = ∠ ABF=90 ° ( )
∵ ∠ CAD= ∠ EBF=30 ° ( )
∴ = ( )
∴ ∥ 。
等式的性质
垂直的性质
BE
∠EBA
内错角相等,两直线平行
∠ABD
AD
已知
已知
继 续
已知:如图直线a、 b被直线c所截,且∠1+∠2=180 °
求证: a ∥b。
你有几种证明方法?
3
4
方法1:
∵ ∠ 1 + ∠ 2 = 180 °
∴ ∠ 2 = ∠ 4
∠ 1 + ∠ 4 = 180 °
∴ a ∥b
(同位角相等,两直线平行)
方法2:
∵ ∠ 1 + ∠ 2 = 180 °
∴ ∠ 2 + ∠ 3= 180 °
∠ 1 = ∠ 3
∴ a ∥b
(同旁内角互补,两直线平行)
小结
证明一个命题的一般步骤:
(1)弄清题设和结论;
(2)根据题意画出相应的图形;
(3)根据题设和结论写出已知,求证;
(4)分析证明思路,写出证明过程.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
