2.2 不等式的基本性质(1) 课件(共17张PPT)
文档属性
| 名称 | 2.2 不等式的基本性质(1) 课件(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 876.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-09 16:55:52 | ||
图片预览




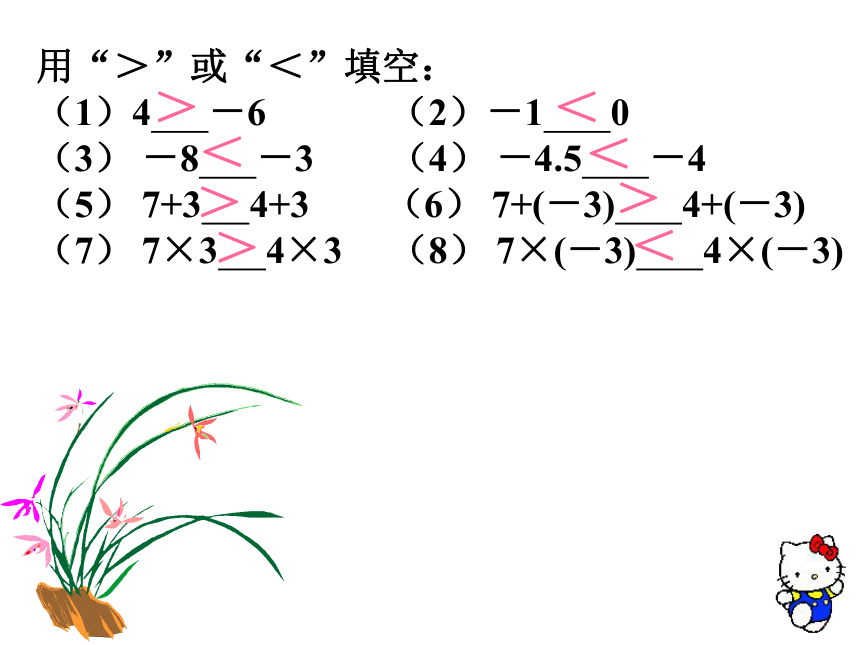
文档简介
(共17张PPT)
1.2不等式的基本性质
北师大版 八年级 下册
第1课时
1、观察下面这几个式子,完成下面的填空。
∵
∴
∴
同一个数
同一个整式
等式的两边都加上(或减去) 或 ,所得的结果仍是等式。
等式的基本性质1:
2、继续观察下面这几个式子,完成下面的填空。
∵
∴
∴
同一个数
等式的两边都乘以(或除以) (除数不能为零),所得的结果仍是等式。
等式的基本性质2:
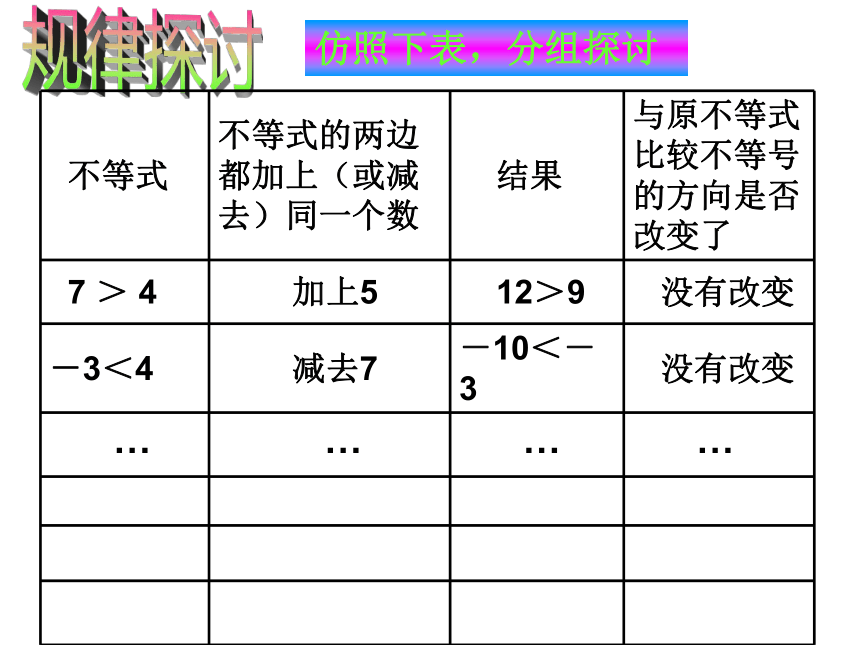
不等式 不等式的两边都加上(或减去)同一个数 结果 与原不等式比较不等号的方向是否改变了
7 > 4 加上5 12>9 没有改变
-3<4 减去7 -10<-3 没有改变
… … … …
仿照下表,分组探讨
不等式的性质1:
不等式的两边都加上(或减去)同一个数,不等号的方向不变。
由上面的探讨我们可以得出:
这个性质可以用数学语言表示为:
如果 ,那么
<
如果 ,那么
>
>
>
>
>
<
<
<
<
用“>”或“<”填空:
(1)4 -6 (2)-1 0
(3) -8 -3 (4) -4.5 -4
(5) 7+3 4+3 (6) 7+(-3) 4+(-3)
(7) 7×3 4×3 (8) 7×(-3) 4×(-3)
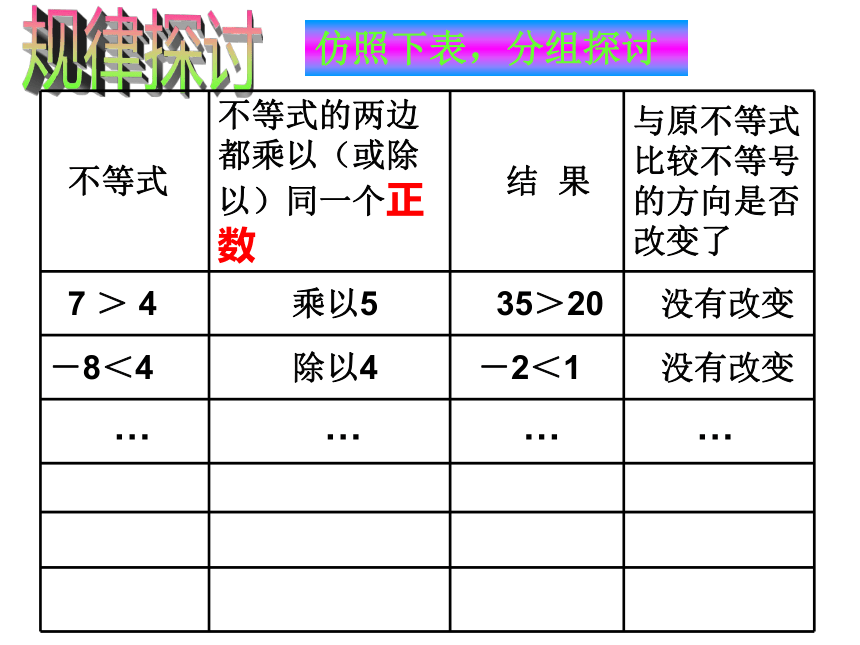
不等式 不等式的两边都乘以(或除以)同一个正数 结 果 与原不等式比较不等号的方向是否改变了
7 > 4 乘以5 35>20 没有改变
-8<4 除以4 -2<1 没有改变
… … … …
仿照下表,分组探讨
不等式的基本性质 2:
不等式的两边都乘以(或除以)同一个正数,不等号的方向不变。
由上面的探讨我们可以继续得出:
如果 , ,那么
如果 , ,那么
这个性质可以用数学语言表示为:
1、如果x+5>4,那么两边都 可得 x >-1
2、在-7<8 的两边都加上9可得 。
3、在5>-2 的两边都减去6可得 。
4、在-3>-4 的两边都乘以7可得 。
5、在-8<0 的两边都除以8 可得 。
减去5
2<17
-1>-8
-21>-28
-1<0
不等式 不等式的两边都乘以(或除以)同一个负数 结 果 与原不等式比较不等号的方向是否改变了
7 > 4 乘以-5 -35<-20 改变了
-8<4 除以-4 2 >-1 改变了
… … … …
仿照下表,分组探讨
不等式的基本性质 3:
不等式的两边都乘以(或除以)同一个负数,不等号的方向要改变。
由上面的探讨我们可以继续得出:
如果 , ,那么
如果 , ,那么
这个性质可以用数学语言表示为:
1、在不等式-8<0的两边都除以-8可得 。
2、在不等式-3 x<3的两边都除以-3可得 。
3、在不等式-3>-4的两边都乘以-3可得 。
4、在不等式 的两边都乘以-1可得 。
1>0
9<12
>
>
>
<
如果 ,那么:
①
②
③
④
(不等式的性质 )
(不等式的性质 )
(不等式的性质 )
(不等式的性质 )
1
2
3
1
解 (1)根据不等式的性质1,两边都加上2得:
x-2+2<3+2
即 x <5
(2)根据不等式的性质1,两边都减去5 x 得:
6 x -5 x <(5 x -1)-5 x
即 x <-1
例 1 根据不等式的基本性质,把下列不等式化成 x< 或 x> 的形式:
(1) x -2< 3 (2) 6 x < 5 x -1
(3) x >5 (4) -4 x >3
③④ 同学回答
是任意有理数,试比较 与 的大小。
解:∵ 5 > 3
∴
这种解法对吗?如果正确,说出它根据的是不等式的哪一条基本性质;如果不正确,请就明理由。
答:这种解法不正确,因为字母 的取值范围我们并不知道。如果 ,那么 ;
如果 ,那么 。
不等式的三条性质是:
① 、不等式的两边都加上(或减去)同一个 数或同一个整式,不等号的方向不变;
② 、不等式的两边都乘以(或除以)同一个 正数,不等号的方向不变;
③ 、*不等式的两边都乘以(或除以)同一个负数,不等号的方向要改变 ;
本节重点
(1)掌握不等式的三条性质,尤其是性质3;
(2)能正确应用性质对不等式进行变形;
当不等式两边都乘以(或除以)同 一个数时,一定要看清是正数还是负数;对于未给定范围的字母,应分情况讨论。
注意事项
1.2不等式的基本性质
北师大版 八年级 下册
第1课时
1、观察下面这几个式子,完成下面的填空。
∵
∴
∴
同一个数
同一个整式
等式的两边都加上(或减去) 或 ,所得的结果仍是等式。
等式的基本性质1:
2、继续观察下面这几个式子,完成下面的填空。
∵
∴
∴
同一个数
等式的两边都乘以(或除以) (除数不能为零),所得的结果仍是等式。
等式的基本性质2:
不等式 不等式的两边都加上(或减去)同一个数 结果 与原不等式比较不等号的方向是否改变了
7 > 4 加上5 12>9 没有改变
-3<4 减去7 -10<-3 没有改变
… … … …
仿照下表,分组探讨
不等式的性质1:
不等式的两边都加上(或减去)同一个数,不等号的方向不变。
由上面的探讨我们可以得出:
这个性质可以用数学语言表示为:
如果 ,那么
<
如果 ,那么
>
>
>
>
>
<
<
<
<
用“>”或“<”填空:
(1)4 -6 (2)-1 0
(3) -8 -3 (4) -4.5 -4
(5) 7+3 4+3 (6) 7+(-3) 4+(-3)
(7) 7×3 4×3 (8) 7×(-3) 4×(-3)
不等式 不等式的两边都乘以(或除以)同一个正数 结 果 与原不等式比较不等号的方向是否改变了
7 > 4 乘以5 35>20 没有改变
-8<4 除以4 -2<1 没有改变
… … … …
仿照下表,分组探讨
不等式的基本性质 2:
不等式的两边都乘以(或除以)同一个正数,不等号的方向不变。
由上面的探讨我们可以继续得出:
如果 , ,那么
如果 , ,那么
这个性质可以用数学语言表示为:
1、如果x+5>4,那么两边都 可得 x >-1
2、在-7<8 的两边都加上9可得 。
3、在5>-2 的两边都减去6可得 。
4、在-3>-4 的两边都乘以7可得 。
5、在-8<0 的两边都除以8 可得 。
减去5
2<17
-1>-8
-21>-28
-1<0
不等式 不等式的两边都乘以(或除以)同一个负数 结 果 与原不等式比较不等号的方向是否改变了
7 > 4 乘以-5 -35<-20 改变了
-8<4 除以-4 2 >-1 改变了
… … … …
仿照下表,分组探讨
不等式的基本性质 3:
不等式的两边都乘以(或除以)同一个负数,不等号的方向要改变。
由上面的探讨我们可以继续得出:
如果 , ,那么
如果 , ,那么
这个性质可以用数学语言表示为:
1、在不等式-8<0的两边都除以-8可得 。
2、在不等式-3 x<3的两边都除以-3可得 。
3、在不等式-3>-4的两边都乘以-3可得 。
4、在不等式 的两边都乘以-1可得 。
1>0
9<12
>
>
>
<
如果 ,那么:
①
②
③
④
(不等式的性质 )
(不等式的性质 )
(不等式的性质 )
(不等式的性质 )
1
2
3
1
解 (1)根据不等式的性质1,两边都加上2得:
x-2+2<3+2
即 x <5
(2)根据不等式的性质1,两边都减去5 x 得:
6 x -5 x <(5 x -1)-5 x
即 x <-1
例 1 根据不等式的基本性质,把下列不等式化成 x< 或 x> 的形式:
(1) x -2< 3 (2) 6 x < 5 x -1
(3) x >5 (4) -4 x >3
③④ 同学回答
是任意有理数,试比较 与 的大小。
解:∵ 5 > 3
∴
这种解法对吗?如果正确,说出它根据的是不等式的哪一条基本性质;如果不正确,请就明理由。
答:这种解法不正确,因为字母 的取值范围我们并不知道。如果 ,那么 ;
如果 ,那么 。
不等式的三条性质是:
① 、不等式的两边都加上(或减去)同一个 数或同一个整式,不等号的方向不变;
② 、不等式的两边都乘以(或除以)同一个 正数,不等号的方向不变;
③ 、*不等式的两边都乘以(或除以)同一个负数,不等号的方向要改变 ;
本节重点
(1)掌握不等式的三条性质,尤其是性质3;
(2)能正确应用性质对不等式进行变形;
当不等式两边都乘以(或除以)同 一个数时,一定要看清是正数还是负数;对于未给定范围的字母,应分情况讨论。
注意事项
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
