人教版数学九上24.1.4圆周角课件(共74张PPT)
文档属性
| 名称 | 人教版数学九上24.1.4圆周角课件(共74张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 07:03:26 | ||
图片预览






文档简介
(共74张PPT)
圆周角
如图是圆柱形的海洋馆横截面的示意图,
学完今天的课程,你们就会知道答案了!
玻璃
弧AB 表示圆弧形玻璃窗.
他们的视角相同吗?
乙、丙分别站在其他靠墙的位置D 和E,
同学甲站在正对着玻璃窗的靠墙的位置C,
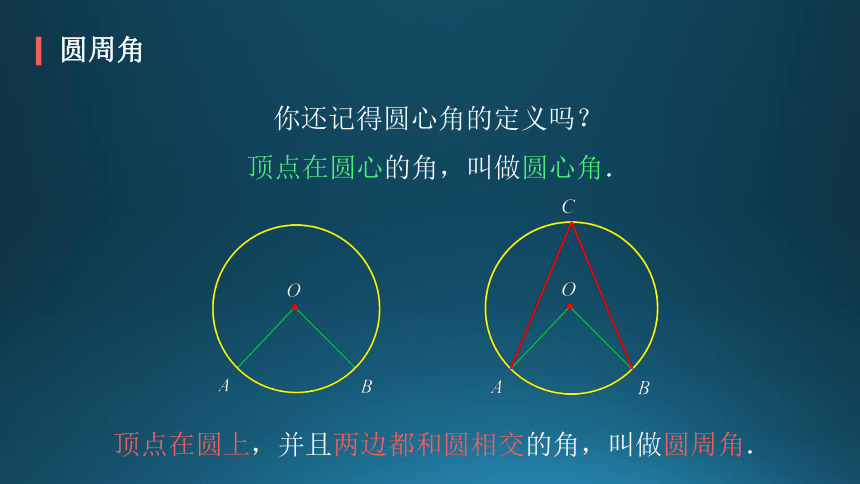
圆周角
你还记得圆心角的定义吗?
顶点在圆心的角,叫做圆心角.
顶点在圆上,并且两边都和圆相交的角,叫做圆周角.
练习
判断下列各图中的角是不是圆周角,为什么?
分别测量图中弧AB所对的圆周角∠ACB和圆心角∠AOB,它们之间有什么关系?
改变C点的位置,再次测量∠ACB 和∠AOB,这个关系还成立吗?
改变B点的位置,再次测量∠ACB 和∠AOB,这个关系还成立吗?
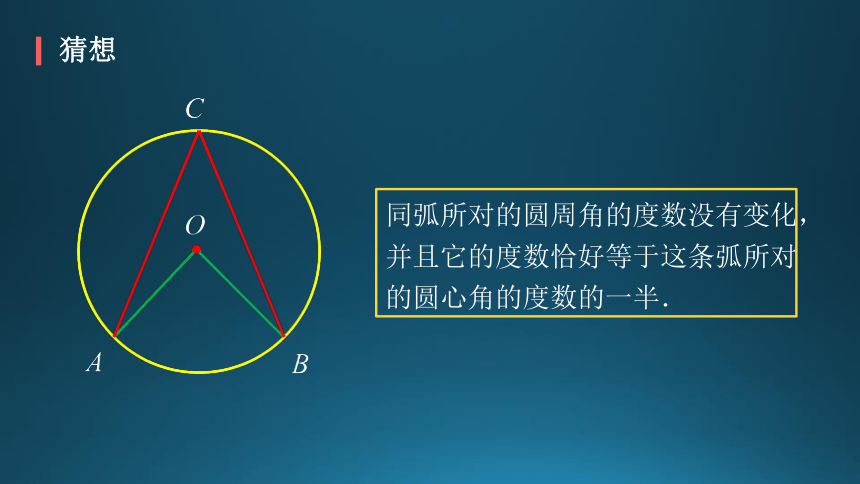
探究
猜想
同弧所对的圆周角的度数没有变化,并且它的度数恰好等于这条弧所对的圆心角的度数的一半.
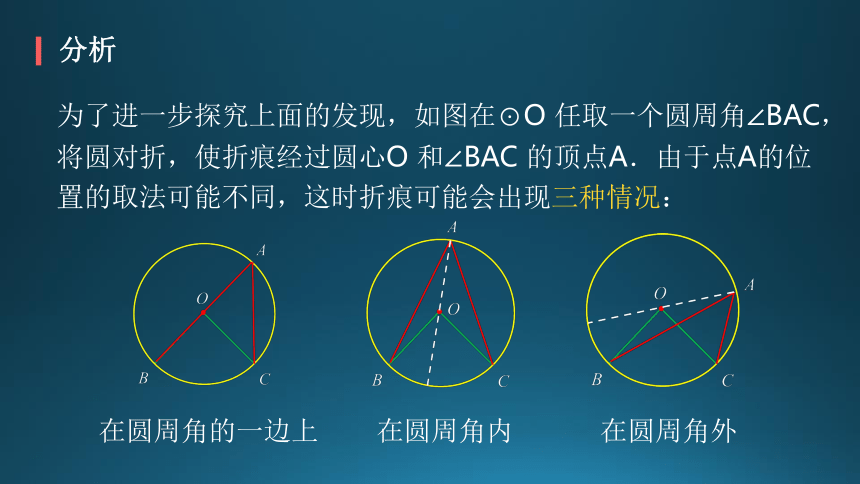
分析
为了进一步探究上面的发现,如图在⊙O 任取一个圆周角∠BAC,将圆对折,使折痕经过圆心O 和∠BAC 的顶点A.由于点A的位置的取法可能不同,这时折痕可能会出现三种情况:
在圆周角的一边上
在圆周角内
在圆周角外
证明
(1)折痕在圆周角的一边上
∵OA=OC,
∴∠A=∠C.
又∠BOC =∠A+∠C
∴∠BOC =2∠A
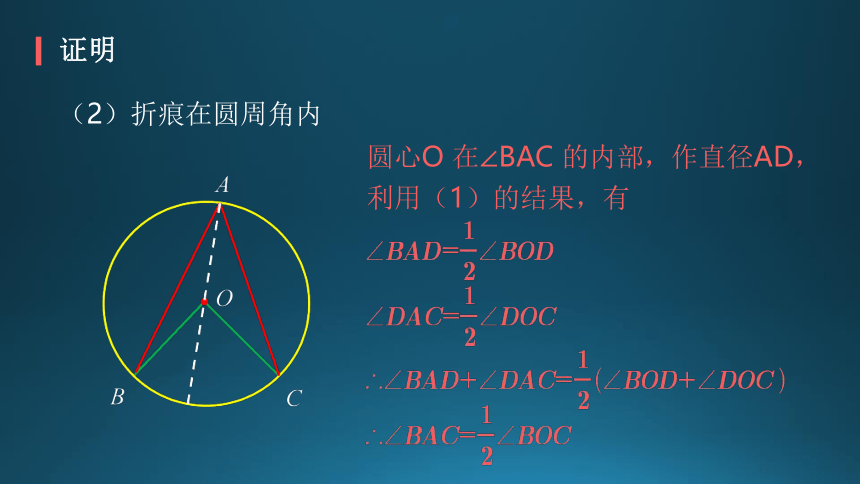
证明
(2)折痕在圆周角内
圆心O 在∠BAC 的内部,作直径AD,
利用(1)的结果,有
证明
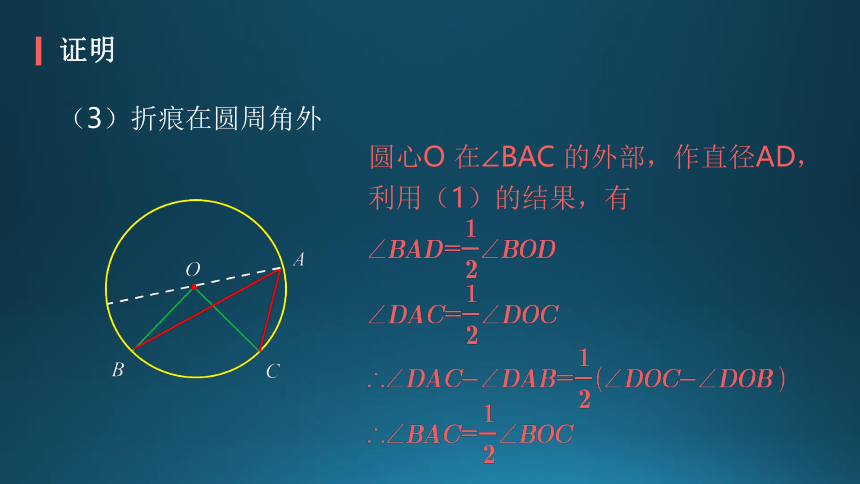
(3)折痕在圆周角外
圆心O 在∠BAC 的外部,作直径AD,
利用(1)的结果,有
圆周角定理
一条弧所对的圆周角等于它所对的圆心角的一半.
练习
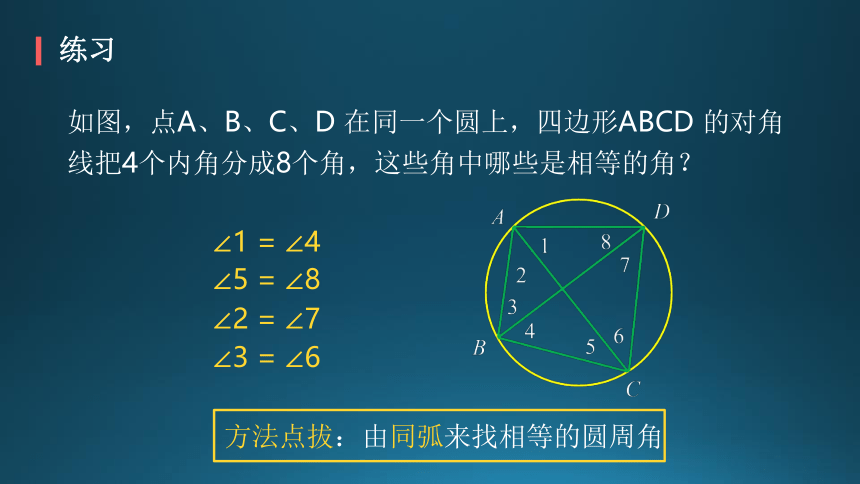
如图,点A、B、C、D 在同一个圆上,四边形ABCD 的对角线把4个内角分成8个角,这些角中哪些是相等的角?
∠1 = ∠4
∠5 = ∠8
∠2 = ∠7
∠3 = ∠6
方法点拔:由同弧来找相等的圆周角
练习
求圆中角α 的度数.
35°
120°
练习
如图,OA、OB、OC 都是⊙O 的半径,∠AOB=2∠BOC,∠ACB与∠BAC 的大小有什么关系?为什么?
答案:∠ACB =2∠BAC.
练习
如图,AB 是⊙O 的直径,∠AOD是圆心角, ∠BCD 是圆周角,若∠BCD =25°,则∠AOD = _______ .
130°
练习
如图,AB 是⊙O 的直径,∠A=30°,点B是弧CD的中点,则∠BOD = _____.
60°
练习
在⊙O 中,∠CBD =30°,∠BDC =20°,求∠A.
提示:连接AC
答案:50°
思考题
如图,在 ⊙O 中,AB 为直径, ,弦CG⊥AB,交AB 于D,交BF 于E.求证:BE =EC.
提示:连接BC
等弧对等角
基于圆周角定理,我们很容易得到如下推理:
同弧或等弧所对的圆周角相等
练习
如图,点A、B、C、D 在⊙O上,若∠C =60°,则∠D = ____ ,∠O = ____ .
60°
120°
练习
如图,等边△ABC 的顶点都在 ⊙O 上,点D 是 ⊙O 上一点,∠BDC = ____ .
60°
直径对直角
如果圆周角定理中的圆弧变成了半圆,就会有如下推论:
半圆(或直径)所对的圆周角是直角
反过来,也成立
90°的圆周角所对的弦是直径
例题
如图,⊙O 的直径 AB 为 10 cm,弦 AC 为 6 cm,∠ACB 的平分线交⊙O 于点 D,求 BC,AD,BD 的长.
解:连接 OD,AD,BD,
∵ AB 是 ⊙O 的直径,
∴ ∠ACB =∠ADB =90°.
在 Rt△ABC 中,
BC = =8(cm)
例题
如图,⊙O 的直径 AB 为 10 cm,弦 AC 为 6 cm,∠ACB 的平分线交⊙O 于点 D,求 BC,AD,BD 的长.
∵ CD 平分∠ACB,
∴ ∠ACD=∠BCD,
∴ ∠AOD=∠BOD .
∴ AD=BD.
在 Rt△ABD 中,
例题
求证:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.
已知:△ABC 中,CO 为AB 边上的中线,且 ,求证: △ABC 为直角三角形.
证明:
以AB 为直径作⊙O,
∵AO=BO,
∴AO=BO=CO.
∴点C 在 ⊙O上.
又∵AB为直径,
∴∠ACB= ×180°= 90°.
∴ △ABC 为直角三角形.
练习
如图,已知△ABC 内接于圆O,AB=AC,∠A=36°,CD 是圆O 的直径,求∠ACD 的度数.
答案:18°.
总结:看到直径就要想到直角.
知识回顾
圆周角定理及其推论是什么?
半圆(或直径)所对的圆周角是直角 90°的圆周角所对的弦是直径.
同弧或等弧所对的圆周角相等
一条弧所对的圆周角等于它所对的圆心角的一半.
知识回顾
判断正误:
1.同弧或等弧所对的圆周角相等( )
2.相等的圆周角所对的弧相等( )
3.90°圆周角所对的弦是直径( )
4.直径所对的角等于90°( )
圆内接多边形
若一个多边形各顶点都在同一个圆上,那么,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆.
圆内接多边形
多边形的外接圆
圆内接四边形
如图,四边形ABCD 为 ⊙O 的内接四边形;⊙O为四边形ABCD的外接圆.
圆内接四边形的四个角之间有什么关系?
对角互补
圆内四边形对角互补
猜想:
圆内四边形对角互补
证明:
∴∠A+∠ C= 180°
同理∠B+∠D=180°
圆的内接四边形的对角互补
如图,四边形ABCD 内接于⊙O,
则∠A+∠C =______ ,∠B+∠ADC =_______;
若∠B=80°,则∠ADC = ____.
练习
180°
180°
100°
练习
四边形ABCD 内接于 ⊙O,∠AOC =100°,则∠B = ______,∠D = ______ .
50°
130°
练习
四边形ABCD 内接于 ⊙O, ∠A:∠C =1:3,则∠A= _____.
45°
练习
若ABCD 为圆内接四边形,则下列哪个选项可能成立( )
A.∠A∶∠B∶∠C∶∠D = 1∶2∶3∶4
B.∠A∶∠B∶∠C∶∠D = 1∶2∶4∶3
C.∠A∶∠B∶∠C∶∠D = 3∶2∶1∶4
D.∠A∶∠B∶∠C∶∠D = 4∶3∶2∶1
B
练习
如图,等边三角形ABC 内接于⊙O,P 是 上的一点,则∠APB = ________.
120°
练习
如图,四边形ABCD 内接于 ⊙O,如果∠BOD=130°,则∠BCD 的度数是 ______.
115°
练习
如图,四边形ABCD 为⊙O 的内接四边形,已知∠BOD=100°,求∠BAD及∠BCD 的度数.
答案:50°,130°
练习
如图,已知四边形ABCD 内接于圆O,点O 在∠A 内部,∠OBA +
∠ODA =50°,则∠C = ______ .
130°
提示:连接AO
练习
如下图左,四边形 ABCD 内接于⊙O,AB 是直径,∠ABD =30°,则∠BCD 的度数为多少?
答案:120°
练习
如图,圆内接四边形ABCD 的两组对边的延长线分别相交于E、F,若∠A=55°,∠E=30°,则∠F = ______.
40°
练习
梯形ABCD 内接于⊙O,AD∥BC, ∠B =75°,则∠C =_____.
75°
圆的内接梯形一定是 ______ 梯形.
等腰
练习
已知:如图,四边形ABCD 是圆的内接四边形并且ABCD 是平行四边形.求证:四边形ABCD 是矩形.
提示:证明∠A=∠B 即可.
练习
1.判断下列图形中的角是不是圆周角,并说明理由:
练习
2.如图,圆内接四边形ABCD 的对角线AC,BD 把它的4个内角分成8个角,这些角中哪些相等?为什么
练习
3.如图,OA,OB,OC,都是 O 的半径,∠AOB=2∠BOC .求证:∠ACB =2∠BAC .
练习
4.如图,你能用三角尺确定一张圆形纸片的圆心吗?有几种方法?与同学交流一下.
练习
5.如图,四边形ABCD 内接于 O,E 为CD 延长线一点 .若∠B =110°,∠ADE 的度数 .
思考题
已知:△ABC 中,AB=AC,D 是△ABC 外接圆上的点(不与 A,C 重合),延长 BD 到 E.求证:AD 的延长线平分∠CDE.
提示:
圆内接四边形的外角等于内对角;
同弧所对圆周角相等.
思考题
如图⊙O 与⊙O 都经过A、B 两点,经过点A 的直线CD 与⊙O 交于点C,与⊙O 交于点D.经过点B 的直线EF 与⊙O 交于点E,与⊙O 交于点F.求证:CE∥DF.
1
2
1
2
1
2
提示1:连接AB.
提示2:圆内接四边形的外角等于其内角的对角.
思考题
如图,在⊙O 中,AB 为直径,直线 l 与⊙O 交于点 C、D,BE⊥l 于点 E,连接 BD、BC.求证:∠CBE =∠ABD.
提示:连接AD.
多解问题
如图所示,AB 为⊙O 的直径,C 为⊙O上一点,且∠AOC =80°,点D 在⊙O上(不与B、C 重合),则∠BDC 的度数是 __________.
50°或130°
提示:D 可能在劣弧BC 上,也可能在优弧BC 上.
如图,AD、BE 是△ABC 的两条高.求证:∠CED =∠ABC.
利用共圆证明
提示:取AB 中点M,连接EM,DM,证明ABDE 四点共圆.
圆的性质综合
如图,已知AE 是圆O 的直径,△ABC 内接于圆O,AD⊥BC 于 D 交圆O于F.
(1)求证:∠BAE =∠CAF.
(2) 若∠ACB =60°,CF =2,求圆O 的半径.
(1)提示:连接EC
(2)提示:连接OF,OC
总结
半圆(或直径)所对的圆周角是直角 90°的圆周角所对的弦是直径.
同弧或等弧所对的圆周角相等
一条弧所对的圆周角等于它所对的圆心角的一半.
这节课我们学会了什么?
总结
若一个多边形各顶点都在同一个圆上,那么,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆.
这节课我们还学会了什么?
圆的内接四边形的对角互补
复习巩固
1.求证:直径是圆中最长的弦 .
复习巩固
2.如图,在半径为 50mm 的 ⊙O 中,弦AB长50mm . 求:
(1)∠AOB 的度数;
(2)点O 到AB 的距离.
复习巩固
3.如图,⊙O 中, ,∠C =75°.求∠A的度数 .
复习巩固
4.如图,AD =BC ,比较 ,并证明你的结论 .
复习巩固
5.如图,⊙O 中, ,∠AOB =50°.求∠ADC 的度数 .
复习巩固
6.如图,用直角曲尺检查圆形的工件,哪个是合格的?为什么?
复习巩固
7.求证:圆内接平行四边形是矩形.
综合运用
8.如下页图是一个隧道的横截面,它的形状是以点O 为圆心的圆的一部分.如果M 是 ⊙O 中CD 的中点,EM 经过圆心O 交圆O 于点E,并且CD =4m.EM =6m.求⊙O 的半径.
综合运用
9.如图,两个圆都以点O 为圆心,大圆的弦AB 交小圆于C , D 两点.求证:AC =BD.
综合运用
10.⊙O 的半径为13cm,AB,CD 是 ⊙O 的两条弦, ,AB =24cm,CD =10cm . 求AB 和CD 之间的距离.
综合运用
11.如图,AB,CD 是 ⊙O 的两条平行弦,MN 是AB 的垂直平行线 . 求证:MN 垂直平分CD .
综合运用
12.如图,一条公路的转弯处是一段圆弧( ),点O是这段弧所在圆的圆心.AB =300m,C 是 上一点,垂足为D,CD =45m.求这段弯路的半径.
综合运用
13.如图,A,B 是⊙O上的两点,∠AOB =120°,C 是 的中点.求证:四边形OACB 是菱形.
综合运用
14.如图,A,P,B,C 是 ⊙O上的四个点,∠APC =∠CPB=60°,判断△ABC 的形状,并证明你的结论.
拓广探索
15.如图,AB 和CD 分别 是 ⊙O上的两条弦,圆心到它们的距离分别是OM 和ON . 如果AB >CD,OM 和ON 的大小有什么关系?为什么?
拓广探索
16.如图,铁路MN和公路PQ 在点O 处交会,∠QON =30°,在点A处有一栋居民楼,AO =200m.如果火车行驶时,周围200m以内会受到噪声的影响,那么火车在铁路MN 上沿ON 方向行驶时,居民楼是否会受到噪声的影响?如果火车行驶的速度为72km/h . 居民楼受噪声影响的时间约为多少秒(结果保留小数点后一位)?
拓广探索
17.如图,一个海港在 范围内是浅滩,为了使深水船只不进入浅滩,需要测量船所在的位置与两个灯塔的视角∠XPY,并把它与已知的危险角∠XZY( 上任意一点Z与两个灯塔所成的角)相较,航行中保持∠XPY <∠XZY . 你知道这样做的道理吗?
圆周角
如图是圆柱形的海洋馆横截面的示意图,
学完今天的课程,你们就会知道答案了!
玻璃
弧AB 表示圆弧形玻璃窗.
他们的视角相同吗?
乙、丙分别站在其他靠墙的位置D 和E,
同学甲站在正对着玻璃窗的靠墙的位置C,
圆周角
你还记得圆心角的定义吗?
顶点在圆心的角,叫做圆心角.
顶点在圆上,并且两边都和圆相交的角,叫做圆周角.
练习
判断下列各图中的角是不是圆周角,为什么?
分别测量图中弧AB所对的圆周角∠ACB和圆心角∠AOB,它们之间有什么关系?
改变C点的位置,再次测量∠ACB 和∠AOB,这个关系还成立吗?
改变B点的位置,再次测量∠ACB 和∠AOB,这个关系还成立吗?
探究
猜想
同弧所对的圆周角的度数没有变化,并且它的度数恰好等于这条弧所对的圆心角的度数的一半.
分析
为了进一步探究上面的发现,如图在⊙O 任取一个圆周角∠BAC,将圆对折,使折痕经过圆心O 和∠BAC 的顶点A.由于点A的位置的取法可能不同,这时折痕可能会出现三种情况:
在圆周角的一边上
在圆周角内
在圆周角外
证明
(1)折痕在圆周角的一边上
∵OA=OC,
∴∠A=∠C.
又∠BOC =∠A+∠C
∴∠BOC =2∠A
证明
(2)折痕在圆周角内
圆心O 在∠BAC 的内部,作直径AD,
利用(1)的结果,有
证明
(3)折痕在圆周角外
圆心O 在∠BAC 的外部,作直径AD,
利用(1)的结果,有
圆周角定理
一条弧所对的圆周角等于它所对的圆心角的一半.
练习
如图,点A、B、C、D 在同一个圆上,四边形ABCD 的对角线把4个内角分成8个角,这些角中哪些是相等的角?
∠1 = ∠4
∠5 = ∠8
∠2 = ∠7
∠3 = ∠6
方法点拔:由同弧来找相等的圆周角
练习
求圆中角α 的度数.
35°
120°
练习
如图,OA、OB、OC 都是⊙O 的半径,∠AOB=2∠BOC,∠ACB与∠BAC 的大小有什么关系?为什么?
答案:∠ACB =2∠BAC.
练习
如图,AB 是⊙O 的直径,∠AOD是圆心角, ∠BCD 是圆周角,若∠BCD =25°,则∠AOD = _______ .
130°
练习
如图,AB 是⊙O 的直径,∠A=30°,点B是弧CD的中点,则∠BOD = _____.
60°
练习
在⊙O 中,∠CBD =30°,∠BDC =20°,求∠A.
提示:连接AC
答案:50°
思考题
如图,在 ⊙O 中,AB 为直径, ,弦CG⊥AB,交AB 于D,交BF 于E.求证:BE =EC.
提示:连接BC
等弧对等角
基于圆周角定理,我们很容易得到如下推理:
同弧或等弧所对的圆周角相等
练习
如图,点A、B、C、D 在⊙O上,若∠C =60°,则∠D = ____ ,∠O = ____ .
60°
120°
练习
如图,等边△ABC 的顶点都在 ⊙O 上,点D 是 ⊙O 上一点,∠BDC = ____ .
60°
直径对直角
如果圆周角定理中的圆弧变成了半圆,就会有如下推论:
半圆(或直径)所对的圆周角是直角
反过来,也成立
90°的圆周角所对的弦是直径
例题
如图,⊙O 的直径 AB 为 10 cm,弦 AC 为 6 cm,∠ACB 的平分线交⊙O 于点 D,求 BC,AD,BD 的长.
解:连接 OD,AD,BD,
∵ AB 是 ⊙O 的直径,
∴ ∠ACB =∠ADB =90°.
在 Rt△ABC 中,
BC = =8(cm)
例题
如图,⊙O 的直径 AB 为 10 cm,弦 AC 为 6 cm,∠ACB 的平分线交⊙O 于点 D,求 BC,AD,BD 的长.
∵ CD 平分∠ACB,
∴ ∠ACD=∠BCD,
∴ ∠AOD=∠BOD .
∴ AD=BD.
在 Rt△ABD 中,
例题
求证:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.
已知:△ABC 中,CO 为AB 边上的中线,且 ,求证: △ABC 为直角三角形.
证明:
以AB 为直径作⊙O,
∵AO=BO,
∴AO=BO=CO.
∴点C 在 ⊙O上.
又∵AB为直径,
∴∠ACB= ×180°= 90°.
∴ △ABC 为直角三角形.
练习
如图,已知△ABC 内接于圆O,AB=AC,∠A=36°,CD 是圆O 的直径,求∠ACD 的度数.
答案:18°.
总结:看到直径就要想到直角.
知识回顾
圆周角定理及其推论是什么?
半圆(或直径)所对的圆周角是直角 90°的圆周角所对的弦是直径.
同弧或等弧所对的圆周角相等
一条弧所对的圆周角等于它所对的圆心角的一半.
知识回顾
判断正误:
1.同弧或等弧所对的圆周角相等( )
2.相等的圆周角所对的弧相等( )
3.90°圆周角所对的弦是直径( )
4.直径所对的角等于90°( )
圆内接多边形
若一个多边形各顶点都在同一个圆上,那么,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆.
圆内接多边形
多边形的外接圆
圆内接四边形
如图,四边形ABCD 为 ⊙O 的内接四边形;⊙O为四边形ABCD的外接圆.
圆内接四边形的四个角之间有什么关系?
对角互补
圆内四边形对角互补
猜想:
圆内四边形对角互补
证明:
∴∠A+∠ C= 180°
同理∠B+∠D=180°
圆的内接四边形的对角互补
如图,四边形ABCD 内接于⊙O,
则∠A+∠C =______ ,∠B+∠ADC =_______;
若∠B=80°,则∠ADC = ____.
练习
180°
180°
100°
练习
四边形ABCD 内接于 ⊙O,∠AOC =100°,则∠B = ______,∠D = ______ .
50°
130°
练习
四边形ABCD 内接于 ⊙O, ∠A:∠C =1:3,则∠A= _____.
45°
练习
若ABCD 为圆内接四边形,则下列哪个选项可能成立( )
A.∠A∶∠B∶∠C∶∠D = 1∶2∶3∶4
B.∠A∶∠B∶∠C∶∠D = 1∶2∶4∶3
C.∠A∶∠B∶∠C∶∠D = 3∶2∶1∶4
D.∠A∶∠B∶∠C∶∠D = 4∶3∶2∶1
B
练习
如图,等边三角形ABC 内接于⊙O,P 是 上的一点,则∠APB = ________.
120°
练习
如图,四边形ABCD 内接于 ⊙O,如果∠BOD=130°,则∠BCD 的度数是 ______.
115°
练习
如图,四边形ABCD 为⊙O 的内接四边形,已知∠BOD=100°,求∠BAD及∠BCD 的度数.
答案:50°,130°
练习
如图,已知四边形ABCD 内接于圆O,点O 在∠A 内部,∠OBA +
∠ODA =50°,则∠C = ______ .
130°
提示:连接AO
练习
如下图左,四边形 ABCD 内接于⊙O,AB 是直径,∠ABD =30°,则∠BCD 的度数为多少?
答案:120°
练习
如图,圆内接四边形ABCD 的两组对边的延长线分别相交于E、F,若∠A=55°,∠E=30°,则∠F = ______.
40°
练习
梯形ABCD 内接于⊙O,AD∥BC, ∠B =75°,则∠C =_____.
75°
圆的内接梯形一定是 ______ 梯形.
等腰
练习
已知:如图,四边形ABCD 是圆的内接四边形并且ABCD 是平行四边形.求证:四边形ABCD 是矩形.
提示:证明∠A=∠B 即可.
练习
1.判断下列图形中的角是不是圆周角,并说明理由:
练习
2.如图,圆内接四边形ABCD 的对角线AC,BD 把它的4个内角分成8个角,这些角中哪些相等?为什么
练习
3.如图,OA,OB,OC,都是 O 的半径,∠AOB=2∠BOC .求证:∠ACB =2∠BAC .
练习
4.如图,你能用三角尺确定一张圆形纸片的圆心吗?有几种方法?与同学交流一下.
练习
5.如图,四边形ABCD 内接于 O,E 为CD 延长线一点 .若∠B =110°,∠ADE 的度数 .
思考题
已知:△ABC 中,AB=AC,D 是△ABC 外接圆上的点(不与 A,C 重合),延长 BD 到 E.求证:AD 的延长线平分∠CDE.
提示:
圆内接四边形的外角等于内对角;
同弧所对圆周角相等.
思考题
如图⊙O 与⊙O 都经过A、B 两点,经过点A 的直线CD 与⊙O 交于点C,与⊙O 交于点D.经过点B 的直线EF 与⊙O 交于点E,与⊙O 交于点F.求证:CE∥DF.
1
2
1
2
1
2
提示1:连接AB.
提示2:圆内接四边形的外角等于其内角的对角.
思考题
如图,在⊙O 中,AB 为直径,直线 l 与⊙O 交于点 C、D,BE⊥l 于点 E,连接 BD、BC.求证:∠CBE =∠ABD.
提示:连接AD.
多解问题
如图所示,AB 为⊙O 的直径,C 为⊙O上一点,且∠AOC =80°,点D 在⊙O上(不与B、C 重合),则∠BDC 的度数是 __________.
50°或130°
提示:D 可能在劣弧BC 上,也可能在优弧BC 上.
如图,AD、BE 是△ABC 的两条高.求证:∠CED =∠ABC.
利用共圆证明
提示:取AB 中点M,连接EM,DM,证明ABDE 四点共圆.
圆的性质综合
如图,已知AE 是圆O 的直径,△ABC 内接于圆O,AD⊥BC 于 D 交圆O于F.
(1)求证:∠BAE =∠CAF.
(2) 若∠ACB =60°,CF =2,求圆O 的半径.
(1)提示:连接EC
(2)提示:连接OF,OC
总结
半圆(或直径)所对的圆周角是直角 90°的圆周角所对的弦是直径.
同弧或等弧所对的圆周角相等
一条弧所对的圆周角等于它所对的圆心角的一半.
这节课我们学会了什么?
总结
若一个多边形各顶点都在同一个圆上,那么,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆.
这节课我们还学会了什么?
圆的内接四边形的对角互补
复习巩固
1.求证:直径是圆中最长的弦 .
复习巩固
2.如图,在半径为 50mm 的 ⊙O 中,弦AB长50mm . 求:
(1)∠AOB 的度数;
(2)点O 到AB 的距离.
复习巩固
3.如图,⊙O 中, ,∠C =75°.求∠A的度数 .
复习巩固
4.如图,AD =BC ,比较 ,并证明你的结论 .
复习巩固
5.如图,⊙O 中, ,∠AOB =50°.求∠ADC 的度数 .
复习巩固
6.如图,用直角曲尺检查圆形的工件,哪个是合格的?为什么?
复习巩固
7.求证:圆内接平行四边形是矩形.
综合运用
8.如下页图是一个隧道的横截面,它的形状是以点O 为圆心的圆的一部分.如果M 是 ⊙O 中CD 的中点,EM 经过圆心O 交圆O 于点E,并且CD =4m.EM =6m.求⊙O 的半径.
综合运用
9.如图,两个圆都以点O 为圆心,大圆的弦AB 交小圆于C , D 两点.求证:AC =BD.
综合运用
10.⊙O 的半径为13cm,AB,CD 是 ⊙O 的两条弦, ,AB =24cm,CD =10cm . 求AB 和CD 之间的距离.
综合运用
11.如图,AB,CD 是 ⊙O 的两条平行弦,MN 是AB 的垂直平行线 . 求证:MN 垂直平分CD .
综合运用
12.如图,一条公路的转弯处是一段圆弧( ),点O是这段弧所在圆的圆心.AB =300m,C 是 上一点,垂足为D,CD =45m.求这段弯路的半径.
综合运用
13.如图,A,B 是⊙O上的两点,∠AOB =120°,C 是 的中点.求证:四边形OACB 是菱形.
综合运用
14.如图,A,P,B,C 是 ⊙O上的四个点,∠APC =∠CPB=60°,判断△ABC 的形状,并证明你的结论.
拓广探索
15.如图,AB 和CD 分别 是 ⊙O上的两条弦,圆心到它们的距离分别是OM 和ON . 如果AB >CD,OM 和ON 的大小有什么关系?为什么?
拓广探索
16.如图,铁路MN和公路PQ 在点O 处交会,∠QON =30°,在点A处有一栋居民楼,AO =200m.如果火车行驶时,周围200m以内会受到噪声的影响,那么火车在铁路MN 上沿ON 方向行驶时,居民楼是否会受到噪声的影响?如果火车行驶的速度为72km/h . 居民楼受噪声影响的时间约为多少秒(结果保留小数点后一位)?
拓广探索
17.如图,一个海港在 范围内是浅滩,为了使深水船只不进入浅滩,需要测量船所在的位置与两个灯塔的视角∠XPY,并把它与已知的危险角∠XZY( 上任意一点Z与两个灯塔所成的角)相较,航行中保持∠XPY <∠XZY . 你知道这样做的道理吗?
同课章节目录
