人教版数学九年级上册24.1.4圆周角课件(共19张PPT)
文档属性
| 名称 | 人教版数学九年级上册24.1.4圆周角课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 548.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 07:05:14 | ||
图片预览




文档简介
(共19张PPT)
24.1.4 圆 周 角
学习目标
1、理解圆周角定义。
2、掌握有关圆周角的定理及推论。
一. 复习引入:
1.圆心角的定义
.
O
B
C
在同圆(或等圆)中,如果圆心角、弧、弦有一组量相等,那么它们所对应的其余两个量都分别相等。
答:顶点在圆心的角叫圆心角
2.上节课我们学习了圆心角、弧、弦三个量之间关系的一个结论,这个结论是什么?
在射门游戏中(如图),球员射中球门的难易程度与他所处的位置B对球门AC的张角(∠ABC)有关.
顶点在圆上,并且两边都与圆相交的角,叫做圆周角.
●O
B
A
C
B
A
C
B
A
C
B
A
C
B
A
C
B
A
C
B
A
C
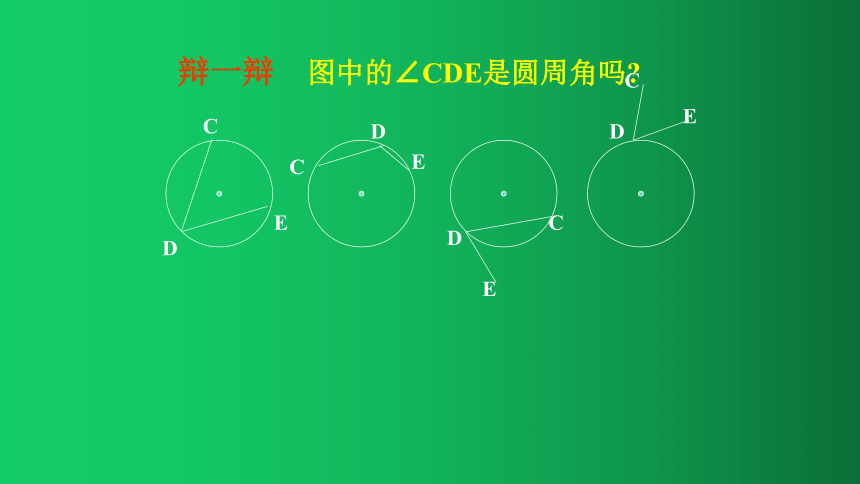
辩一辩 图中的∠CDE是圆周角吗
C
D
E
C
D
E
C
D
E
C
D
E
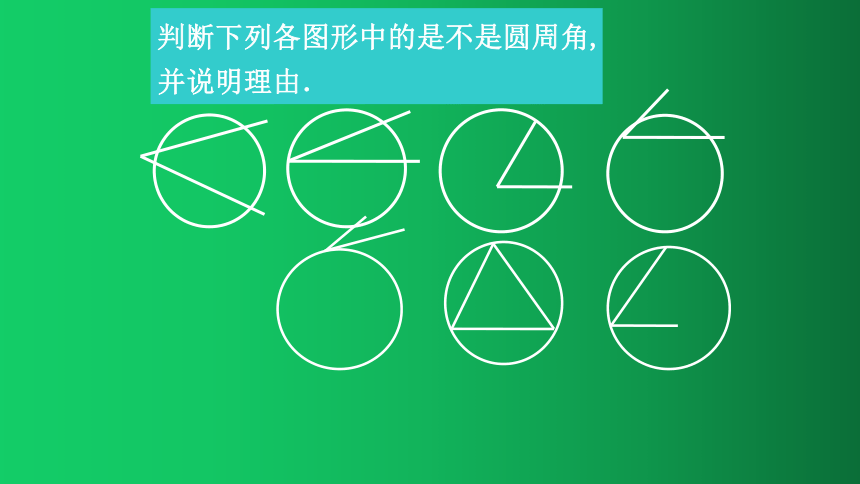
判断下列各图形中的是不是圆周角,
并说明理由.
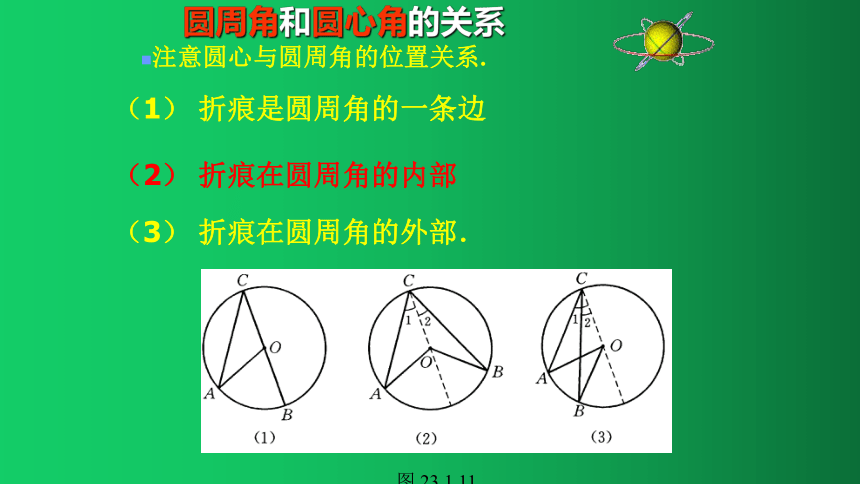
圆周角和圆心角的关系
注意圆心与圆周角的位置关系.
(1) 折痕是圆周角的一条边
(2) 折痕在圆周角的内部
(3) 折痕在圆周角的外部.
综上所述,圆周角∠ABC与圆心角∠AOC的大小关系是:
同弧所对的圆周角等于它所对的圆心角的一半.
●O
A
B
C
●O
A
B
C
●O
A
B
C
即 ∠ABC = ∠AOC.
圆周角和圆心角的关系
1.首先考虑一种特殊情况:
当圆心(O)在圆周角(∠ABC)的一边(BC)上时,圆周角∠ABC与圆心角∠AOC的大小关系.
∵∠AOC是△ABO的外角,
∴∠AOC=∠B+∠A.
∵OA=OB,
●O
A
B
C
∴∠A=∠B.
∴∠AOC=2∠B.
即 ∠ABC = ∠AOC.
你能写出这个命题吗
同弧所对的圆周角等于它所对的圆心角的一半.
综上所述,圆周角∠ABC与圆心角∠AOC的大小关系是:
同弧所对的圆周角等于它所对的圆心角的一半.
●O
A
B
C
●O
A
B
C
●O
A
B
C
即 ∠ABC = ∠AOC.
1.如图,在⊙O中,∠BOC=50°,求∠A的大小.
●O
B
A
C
解: ∠A = ∠BOC = 25°.
A
B
O
C
如图,AB是直径,则∠ACB=____
90 度
半圆(或直径)所对的圆周角是直角,
90度的圆周角所对的弦是直径。
圆周角定理
一条弧所对的圆周角等于它所对圆心角的一半.
同弧所对的圆周角相等
O
E
C
D
B
A
1.试找出下图中所有相等的圆周角。
A
B
C
D
1
2
3
4
5
6
7
8
∠2=∠7
∠1=∠4
∠3=∠6
∠5=∠8
课堂练习
2、下面图形中的角,是圆周角的是( B )
3、如图所示,OA,OB,OC都是☉O的半径,∠ACB=45°,∠BOC=30°,求∠BAC与∠AOB的度数.
分析:根据同弧所对的圆周角等于这条弧所对的圆心角的一半得出∠BAC= ∠BOC=15°,∠AOB=2∠ACB=90°.
解:∵OA,OB,OC都是☉O的半径,∠ACB=45°,∠BOC=30°,∴∠BAC= ∠BOC=15°,
∠AOB=2∠ACB=90°.
能力提升
1、在⊙O中,∠CBD=30° ,∠BDC=20°,求∠A
2、求圆中角X的度数
B
A
O
.
70°
x
A
O
.
X
120°
600
B
P
课堂总结
1.顶点在圆上,并且两边都与圆相交的角,叫做圆周角.
2.同弧所对的圆周角等于它所对的圆心角的一半
3.半圆(或直径)所对的圆周角是直角,
4.90度的圆周角所对的弦是直径。
谢谢
24.1.4 圆 周 角
学习目标
1、理解圆周角定义。
2、掌握有关圆周角的定理及推论。
一. 复习引入:
1.圆心角的定义
.
O
B
C
在同圆(或等圆)中,如果圆心角、弧、弦有一组量相等,那么它们所对应的其余两个量都分别相等。
答:顶点在圆心的角叫圆心角
2.上节课我们学习了圆心角、弧、弦三个量之间关系的一个结论,这个结论是什么?
在射门游戏中(如图),球员射中球门的难易程度与他所处的位置B对球门AC的张角(∠ABC)有关.
顶点在圆上,并且两边都与圆相交的角,叫做圆周角.
●O
B
A
C
B
A
C
B
A
C
B
A
C
B
A
C
B
A
C
B
A
C
辩一辩 图中的∠CDE是圆周角吗
C
D
E
C
D
E
C
D
E
C
D
E
判断下列各图形中的是不是圆周角,
并说明理由.
圆周角和圆心角的关系
注意圆心与圆周角的位置关系.
(1) 折痕是圆周角的一条边
(2) 折痕在圆周角的内部
(3) 折痕在圆周角的外部.
综上所述,圆周角∠ABC与圆心角∠AOC的大小关系是:
同弧所对的圆周角等于它所对的圆心角的一半.
●O
A
B
C
●O
A
B
C
●O
A
B
C
即 ∠ABC = ∠AOC.
圆周角和圆心角的关系
1.首先考虑一种特殊情况:
当圆心(O)在圆周角(∠ABC)的一边(BC)上时,圆周角∠ABC与圆心角∠AOC的大小关系.
∵∠AOC是△ABO的外角,
∴∠AOC=∠B+∠A.
∵OA=OB,
●O
A
B
C
∴∠A=∠B.
∴∠AOC=2∠B.
即 ∠ABC = ∠AOC.
你能写出这个命题吗
同弧所对的圆周角等于它所对的圆心角的一半.
综上所述,圆周角∠ABC与圆心角∠AOC的大小关系是:
同弧所对的圆周角等于它所对的圆心角的一半.
●O
A
B
C
●O
A
B
C
●O
A
B
C
即 ∠ABC = ∠AOC.
1.如图,在⊙O中,∠BOC=50°,求∠A的大小.
●O
B
A
C
解: ∠A = ∠BOC = 25°.
A
B
O
C
如图,AB是直径,则∠ACB=____
90 度
半圆(或直径)所对的圆周角是直角,
90度的圆周角所对的弦是直径。
圆周角定理
一条弧所对的圆周角等于它所对圆心角的一半.
同弧所对的圆周角相等
O
E
C
D
B
A
1.试找出下图中所有相等的圆周角。
A
B
C
D
1
2
3
4
5
6
7
8
∠2=∠7
∠1=∠4
∠3=∠6
∠5=∠8
课堂练习
2、下面图形中的角,是圆周角的是( B )
3、如图所示,OA,OB,OC都是☉O的半径,∠ACB=45°,∠BOC=30°,求∠BAC与∠AOB的度数.
分析:根据同弧所对的圆周角等于这条弧所对的圆心角的一半得出∠BAC= ∠BOC=15°,∠AOB=2∠ACB=90°.
解:∵OA,OB,OC都是☉O的半径,∠ACB=45°,∠BOC=30°,∴∠BAC= ∠BOC=15°,
∠AOB=2∠ACB=90°.
能力提升
1、在⊙O中,∠CBD=30° ,∠BDC=20°,求∠A
2、求圆中角X的度数
B
A
O
.
70°
x
A
O
.
X
120°
600
B
P
课堂总结
1.顶点在圆上,并且两边都与圆相交的角,叫做圆周角.
2.同弧所对的圆周角等于它所对的圆心角的一半
3.半圆(或直径)所对的圆周角是直角,
4.90度的圆周角所对的弦是直径。
谢谢
同课章节目录
