人教版七年级数学下册5.1.1 对顶角 教案(表格式)
文档属性
| 名称 | 人教版七年级数学下册5.1.1 对顶角 教案(表格式) |

|
|
| 格式 | doc | ||
| 文件大小 | 198.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 07:07:47 | ||
图片预览

文档简介
《对顶角》教学设计
学科 七年级数学 教学内容(课名) 5.1相交线
该内容总课时 3 翻转课时 1
一、学习内容分析
1.本节课是人教版七年级数学下册第五章5.1相交线中的内容。教学重点是:⑴理解对顶角的概念.⑵探索并掌握对顶角相等的性质.教学难点是:探索并掌握对顶角相等的性质.2.平面内两条直线的位置关系是“图形与几何”所要研究的基本问题,这些内容学生在前两个学段已经有所接触。本节课在学习了前一节内容邻补角的经验和基础上,继续研究两条直线相交的情形,探究了两直线相交所成的角的位置和大小关系,给出了对顶角概念,得出了“对顶角相等”的结论. 3.对于推理能力的培养,在本章,不仅要求学生通过观察、思考、探究等活动归纳出图形的概念和性质,还要求“说理”和“简单推理”,并了解证明,把推理和证明作为探究得出结论的自然延续.例如“对顶角相等”性质的得出.
二、学习目标分析
1.学习目标:⑴理解对顶角的概念.⑵探索并掌握对顶角相等的性质.2.学习目标分析:⑴对顶角概念的描述要结合图形进行,这样便于学生抓住问题的本质.对顶角是两条相交直线形成的,这是一个前提条件,其中有公共顶点没有公共边(相对)的两个角.⑵对顶角的性质“对顶角相等”是这一节的重点内容,它在以后“几何与图形”知识的学习中经常要用到.这个性质的说理过程开始用“因为…所以…”的形式,从此开始逐步培养学生规范的推理表达.3.目标达成指标:(1)能准确找出相交线中的对顶角;(2)会根据对顶角概念判断哪些角是对顶角;(3)会利用“对顶角相等”这一性质进行简单计算。
三、学习者特征分析
学生已经初步认识了两条直线相交的情况,能够找出其中的邻补角,知道一对邻补角的位置特征和数量关系,并能解决一些简单的几何问题。在学习方法和能力上,学生已经具备了初步的自学、讨论、观察、操作、说理等方法和能力,这都为本节课教学活动的开展提供了有力的知识和能力背景。
四、课前任务设计
1.学生准备:三角尺、量角器、木条(或硬纸条)两根;2.学习资源:①课本;②“对顶角”教学视频:3.学习任务:①阅读课本P2,勾画出对顶角的概念和性质;②认真观看“对顶角”教学视频,完成下列任务:a.知道什么是对顶角: 有公共顶点,且角的两边互为反向延长线的两个角叫做对顶角。b.总结判断对顶角的方法: 对顶角成对出现;有公共顶点;角的两边互为反向延长线。c.完成视频中练一练;d. 完成视频中做一做;4.尝试用“因为……所以……”“由……得……”等完成拓展练习。
五、课上任务设计
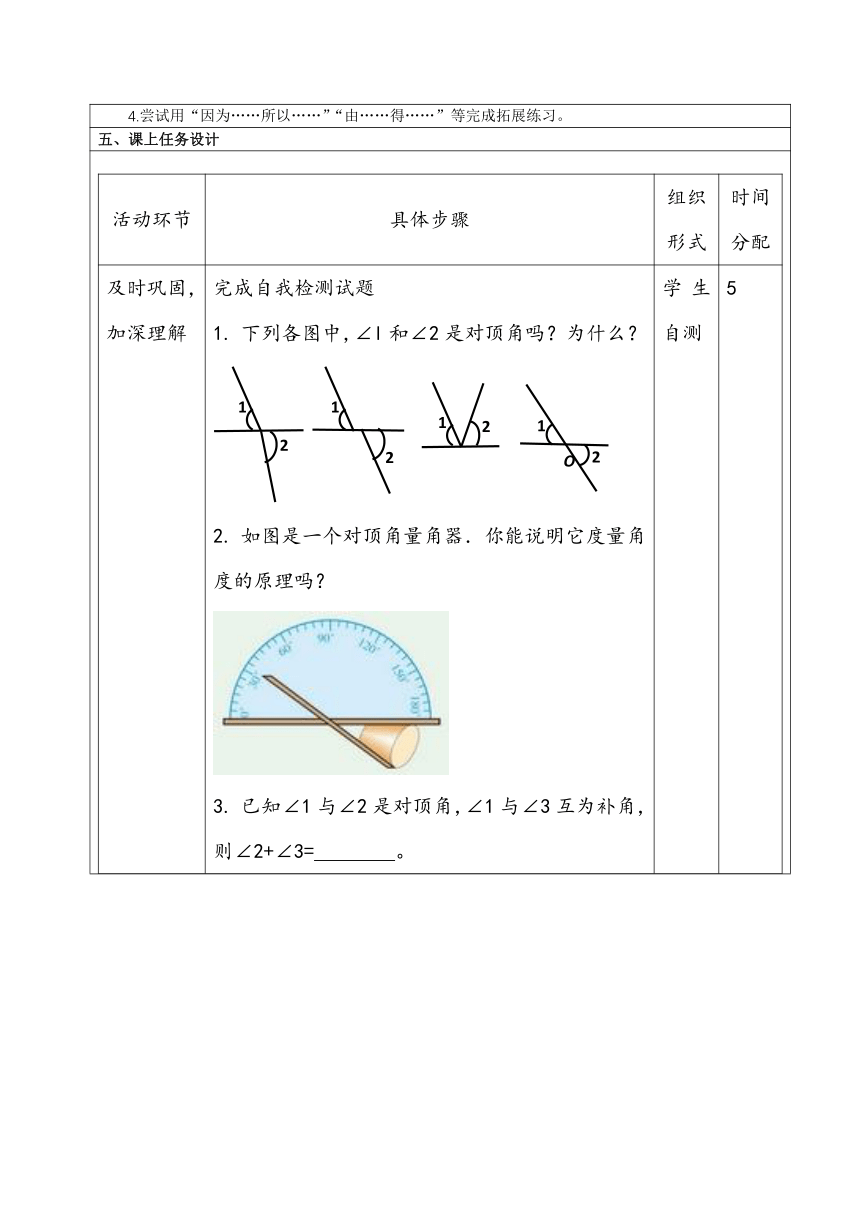
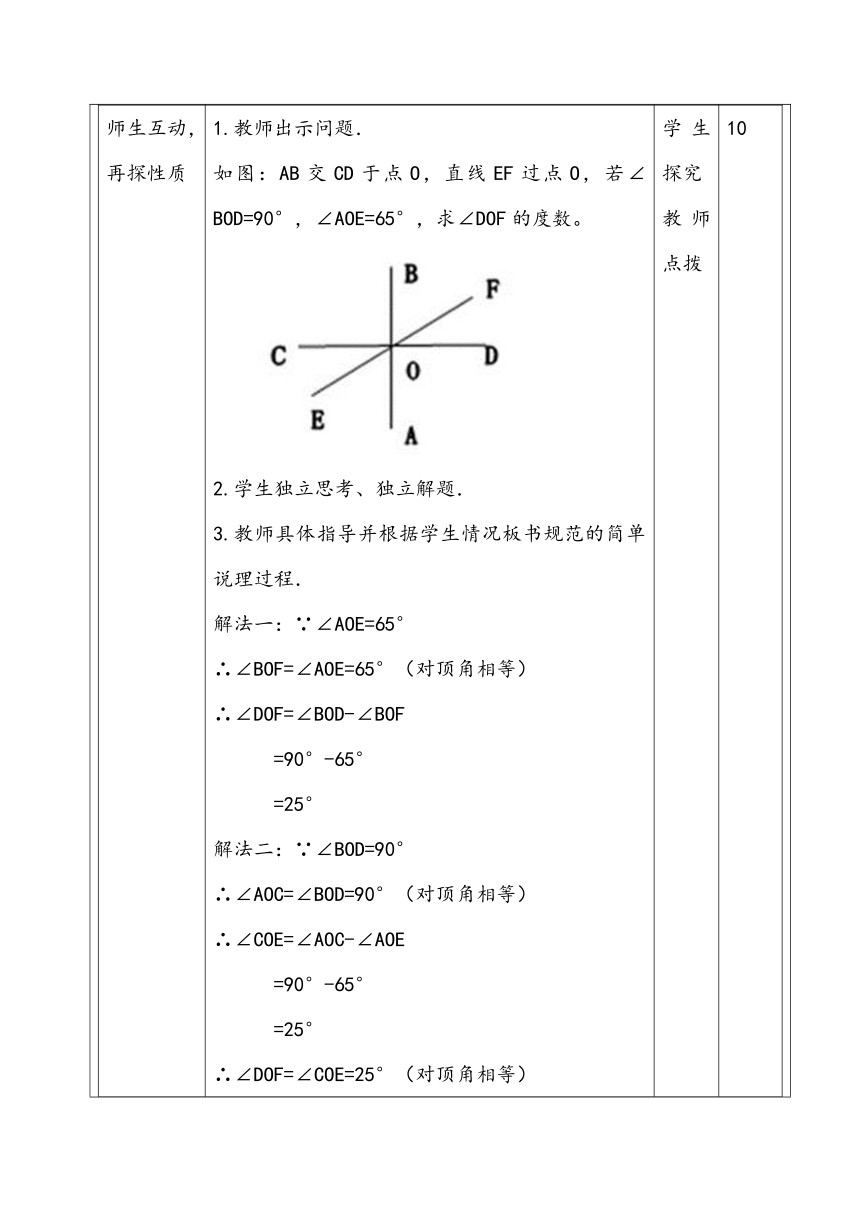
活动环节具体步骤组织形式时间分配及时巩固,加深理解完成自我检测试题1. 下列各图中,∠l和∠2是对顶角吗?为什么?2. 如图是一个对顶角量角器.你能说明它度量角度的原理吗?3. 已知∠1与∠2是对顶角,∠1与∠3互为补角,则∠2+∠3= 。学生自测5师生互动,再探性质1.教师出示问题.如图:AB交CD于点O,直线EF过点O,若∠BOD=90°,∠AOE=65°,求∠DOF的度数。2.学生独立思考、独立解题.3.教师具体指导并根据学生情况板书规范的简单说理过程.解法一:∵∠AOE=65°∴∠BOF=∠AOE=65°(对顶角相等)∴∠DOF=∠BOD-∠BOF=90°-65°=25°解法二:∵∠BOD=90°∴∠AOC=∠BOD=90°(对顶角相等)∴∠COE=∠AOC-∠AOE=90°-65°=25°∴∠DOF=∠COE=25°(对顶角相等)本次活动中,教师应关注:(1)学生对对顶角相等的掌握情况.(2)学生进行简单说理的准确性、规范性.(3)学生能否在独立思考的基础上,积极参与数学问题的讨论.(4)是否能用几何符号语言来表达自己的解题过程.学生探究教师点拨10变式训练,提升能力一、教师出示问题:已知直线a、b相交,∠l=40°,求∠2、∠3、∠4的度数.二、学生进行脑风暴,以小组为单位改变原题中的某一个条件或结论,编制一道试题,并解答。变式1:把∠l=40°变为∠l=90°,求∠2、∠3、∠4的度数.变式2:把∠l=40°变为∠l=n°,求∠2、∠3、∠4的度数.变式3:把∠l=40°改为∠2是∠l的3倍,求∠1、∠2∠3、∠4的度数.变式4:如图,直线AB、CD相交于O点,OE平分∠AOD,若∠1=20°,那么∠2=______.变式5:如图,直线AB、CD相交于O点,∠AOE=90°,若∠1=20°,那么∠2=____,∠3=____,∠4=____.小组合作学习15回顾梳理,归纳小结想一想:通过本节课的学习,你学到了哪些数学知识?你是怎样学习的?学习过程中由知识所反映的数学思想方法有哪些?小组讨论展示10
六、教学设计反思
1.有意识地培养学生有条理的思考和表达对于推理能力的培养,本套教科书按照“说点儿理”“说理”“简单推理”“用符号表示推理”等不同层次分阶段逐步加深地安排.本章对于推理的要求还处在初步阶段,只是结合知识的学习,识图、画图、几何语言的训练从“说理”过渡到“简单推理”.本节课在推导“对顶角相等”这个结论时,采用了用语言叙述的方式进行“说理”,教学中要注意循序渐进逐步提高学生的推理能力,要鼓励学生用自己的语言说明理由,在书写格式上不作统一要求,可以用自然语言,可以结合图形进行说明,可以用箭头等形式表明自己的思路,也可以用数学符号语言表示说理、简单推理的过程,等等.总之,要注意逐步提高、不要急于要求学生用数学符号语言书写,不能操之过急.2.注意突出重点内容这一章的内容比较丰富,除了要研究平面内两条直线间的位置关系(重点是垂直和平行关系),还包括平移以及一些有关命题的内容,由于教学时间有限,为了使学生集中精力掌握最基础的知识,并形成一定的能力,教学时应注意突出重点. 由于内容较多,每课教学时都要突出一两个重点,课堂活动也要围绕这一两个重点进行.本节课要抓住“对顶角相等”这个重点.在课堂上识图、画图、语言训练、作练习都可以主要围绕找“对顶角”或应用“对顶角相等”进行.3.重视信息技术的应用信息技术工具的使用能为学生的数学学习和发展提供丰富多彩的教育环境和有力的学习工具.利用信息技术工具,可以很方便地制作图形,可以很方便地让图形动起来.许多计算机软件还具有测量功能,这也有利于我们在图形的运动变化的过程中去发现其中的不变的位置关系和数量关系,有利于发现图形的性质,这可以使得许多传统的数学教学做不到或做不好的事情变得容易起来.在这一章,信息技术工具是大有用武之地的,教科书还专门安排了一个“信息技术应用”的选学栏目,对教科书中一些可以应用信息技术的地方进行了举例说明.例如,我们随意画两条相交直线,就得到了一个相交线的“模型”,这个模型比我们用木条做成的模型又进一步,它不仅可以随意转动,通过寻找转动过程中角的不变的位置关系得到邻补角和对顶角;还可以利用软件的测量功能,测出这些角的大小,再观察转动过程中角的大小的变化,去发现邻补角、特别是对顶角之间的数量关系,这是传统方法所不能做到的,也正是信息技术工具的优势所在.其他探索垂线的性质、探索平行线的性质和判定方法也是类似的.因此,有条件的学校,应尽可能多的使用计算机或图形计算器等信息技术工具,帮助学生的数学学习.
1
2
1
2
1
2
O
1
2
a
b
1
4
2
32
A
B
E
C
D
O
1
2
学科 七年级数学 教学内容(课名) 5.1相交线
该内容总课时 3 翻转课时 1
一、学习内容分析
1.本节课是人教版七年级数学下册第五章5.1相交线中的内容。教学重点是:⑴理解对顶角的概念.⑵探索并掌握对顶角相等的性质.教学难点是:探索并掌握对顶角相等的性质.2.平面内两条直线的位置关系是“图形与几何”所要研究的基本问题,这些内容学生在前两个学段已经有所接触。本节课在学习了前一节内容邻补角的经验和基础上,继续研究两条直线相交的情形,探究了两直线相交所成的角的位置和大小关系,给出了对顶角概念,得出了“对顶角相等”的结论. 3.对于推理能力的培养,在本章,不仅要求学生通过观察、思考、探究等活动归纳出图形的概念和性质,还要求“说理”和“简单推理”,并了解证明,把推理和证明作为探究得出结论的自然延续.例如“对顶角相等”性质的得出.
二、学习目标分析
1.学习目标:⑴理解对顶角的概念.⑵探索并掌握对顶角相等的性质.2.学习目标分析:⑴对顶角概念的描述要结合图形进行,这样便于学生抓住问题的本质.对顶角是两条相交直线形成的,这是一个前提条件,其中有公共顶点没有公共边(相对)的两个角.⑵对顶角的性质“对顶角相等”是这一节的重点内容,它在以后“几何与图形”知识的学习中经常要用到.这个性质的说理过程开始用“因为…所以…”的形式,从此开始逐步培养学生规范的推理表达.3.目标达成指标:(1)能准确找出相交线中的对顶角;(2)会根据对顶角概念判断哪些角是对顶角;(3)会利用“对顶角相等”这一性质进行简单计算。
三、学习者特征分析
学生已经初步认识了两条直线相交的情况,能够找出其中的邻补角,知道一对邻补角的位置特征和数量关系,并能解决一些简单的几何问题。在学习方法和能力上,学生已经具备了初步的自学、讨论、观察、操作、说理等方法和能力,这都为本节课教学活动的开展提供了有力的知识和能力背景。
四、课前任务设计
1.学生准备:三角尺、量角器、木条(或硬纸条)两根;2.学习资源:①课本;②“对顶角”教学视频:3.学习任务:①阅读课本P2,勾画出对顶角的概念和性质;②认真观看“对顶角”教学视频,完成下列任务:a.知道什么是对顶角: 有公共顶点,且角的两边互为反向延长线的两个角叫做对顶角。b.总结判断对顶角的方法: 对顶角成对出现;有公共顶点;角的两边互为反向延长线。c.完成视频中练一练;d. 完成视频中做一做;4.尝试用“因为……所以……”“由……得……”等完成拓展练习。
五、课上任务设计
活动环节具体步骤组织形式时间分配及时巩固,加深理解完成自我检测试题1. 下列各图中,∠l和∠2是对顶角吗?为什么?2. 如图是一个对顶角量角器.你能说明它度量角度的原理吗?3. 已知∠1与∠2是对顶角,∠1与∠3互为补角,则∠2+∠3= 。学生自测5师生互动,再探性质1.教师出示问题.如图:AB交CD于点O,直线EF过点O,若∠BOD=90°,∠AOE=65°,求∠DOF的度数。2.学生独立思考、独立解题.3.教师具体指导并根据学生情况板书规范的简单说理过程.解法一:∵∠AOE=65°∴∠BOF=∠AOE=65°(对顶角相等)∴∠DOF=∠BOD-∠BOF=90°-65°=25°解法二:∵∠BOD=90°∴∠AOC=∠BOD=90°(对顶角相等)∴∠COE=∠AOC-∠AOE=90°-65°=25°∴∠DOF=∠COE=25°(对顶角相等)本次活动中,教师应关注:(1)学生对对顶角相等的掌握情况.(2)学生进行简单说理的准确性、规范性.(3)学生能否在独立思考的基础上,积极参与数学问题的讨论.(4)是否能用几何符号语言来表达自己的解题过程.学生探究教师点拨10变式训练,提升能力一、教师出示问题:已知直线a、b相交,∠l=40°,求∠2、∠3、∠4的度数.二、学生进行脑风暴,以小组为单位改变原题中的某一个条件或结论,编制一道试题,并解答。变式1:把∠l=40°变为∠l=90°,求∠2、∠3、∠4的度数.变式2:把∠l=40°变为∠l=n°,求∠2、∠3、∠4的度数.变式3:把∠l=40°改为∠2是∠l的3倍,求∠1、∠2∠3、∠4的度数.变式4:如图,直线AB、CD相交于O点,OE平分∠AOD,若∠1=20°,那么∠2=______.变式5:如图,直线AB、CD相交于O点,∠AOE=90°,若∠1=20°,那么∠2=____,∠3=____,∠4=____.小组合作学习15回顾梳理,归纳小结想一想:通过本节课的学习,你学到了哪些数学知识?你是怎样学习的?学习过程中由知识所反映的数学思想方法有哪些?小组讨论展示10
六、教学设计反思
1.有意识地培养学生有条理的思考和表达对于推理能力的培养,本套教科书按照“说点儿理”“说理”“简单推理”“用符号表示推理”等不同层次分阶段逐步加深地安排.本章对于推理的要求还处在初步阶段,只是结合知识的学习,识图、画图、几何语言的训练从“说理”过渡到“简单推理”.本节课在推导“对顶角相等”这个结论时,采用了用语言叙述的方式进行“说理”,教学中要注意循序渐进逐步提高学生的推理能力,要鼓励学生用自己的语言说明理由,在书写格式上不作统一要求,可以用自然语言,可以结合图形进行说明,可以用箭头等形式表明自己的思路,也可以用数学符号语言表示说理、简单推理的过程,等等.总之,要注意逐步提高、不要急于要求学生用数学符号语言书写,不能操之过急.2.注意突出重点内容这一章的内容比较丰富,除了要研究平面内两条直线间的位置关系(重点是垂直和平行关系),还包括平移以及一些有关命题的内容,由于教学时间有限,为了使学生集中精力掌握最基础的知识,并形成一定的能力,教学时应注意突出重点. 由于内容较多,每课教学时都要突出一两个重点,课堂活动也要围绕这一两个重点进行.本节课要抓住“对顶角相等”这个重点.在课堂上识图、画图、语言训练、作练习都可以主要围绕找“对顶角”或应用“对顶角相等”进行.3.重视信息技术的应用信息技术工具的使用能为学生的数学学习和发展提供丰富多彩的教育环境和有力的学习工具.利用信息技术工具,可以很方便地制作图形,可以很方便地让图形动起来.许多计算机软件还具有测量功能,这也有利于我们在图形的运动变化的过程中去发现其中的不变的位置关系和数量关系,有利于发现图形的性质,这可以使得许多传统的数学教学做不到或做不好的事情变得容易起来.在这一章,信息技术工具是大有用武之地的,教科书还专门安排了一个“信息技术应用”的选学栏目,对教科书中一些可以应用信息技术的地方进行了举例说明.例如,我们随意画两条相交直线,就得到了一个相交线的“模型”,这个模型比我们用木条做成的模型又进一步,它不仅可以随意转动,通过寻找转动过程中角的不变的位置关系得到邻补角和对顶角;还可以利用软件的测量功能,测出这些角的大小,再观察转动过程中角的大小的变化,去发现邻补角、特别是对顶角之间的数量关系,这是传统方法所不能做到的,也正是信息技术工具的优势所在.其他探索垂线的性质、探索平行线的性质和判定方法也是类似的.因此,有条件的学校,应尽可能多的使用计算机或图形计算器等信息技术工具,帮助学生的数学学习.
1
2
1
2
1
2
O
1
2
a
b
1
4
2
32
A
B
E
C
D
O
1
2
