人教版七年级数学下册第七章平面直角坐标系本章复习教案
文档属性
| 名称 | 人教版七年级数学下册第七章平面直角坐标系本章复习教案 |  | |
| 格式 | doc | ||
| 文件大小 | 152.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:32:02 | ||
图片预览


文档简介
平面直角坐标系复习
教学目标:
1.能准确画出平面直角坐标系,由点的位置写出坐标,由点的坐标确定点的位置.掌握特殊位置点的坐标特征,并能用坐标表示平移变换.
2.会建立适当的平面直角坐标系,用坐标表示地理位置.
3.通过观察、尝试、交流,提高学生数形结合思想,培养学生归纳,整理所学知识和应用数学的意识.
教学重点:
1.准确确定平面内点的位置和坐标,并能进行综合应用.
2.根据实际问题建立适当的平面直角坐标系,并解决实际问题
教学难点:
1.正确运用坐标特征解决实际问题.
2.平面直角坐标系的实际应用.
教学方法:启发、讨论、交流.
教学过程:
1、 创设情景,导入新课
这是一张某市旅游景点示意图,我们以中心广场所在水平线为横轴,以中心广场所在铅垂线为纵轴建立平面直角坐标系,你们能说出各景点的坐标吗?
平面直角坐标系是确定平面内点的坐标的重要工具,用它可以解决很多实际问题,本节课我们大家一起来复面直角坐标系”这一章.(由一个具体实例引出课题,可激发学生的兴趣,创造积极的求知氛围)
二、师生互动,构建知识框架
1.有序数对:有序数对是指______的两个数组成的数对,它的表示形式是(a,b).
2.平面直角坐标系的意义:在平面内,两条具有 、并且______的数轴所构成的图形叫做平面直角坐标系,其中水平的数轴叫做______或_______,取向______方向为正方向,竖直的数轴叫做______或_______,取向______方向为正方向,横轴与纵轴的交点叫做平面直角坐标系的______,平面直角坐标系的两条数轴把坐标平面分成四个象限,这两条数轴的正方向的所夹的象限叫做第______象限,其它三个象限按逆时针方向依次叫做第______、______、______象限,坐标轴不属于任何象限.
注意:(1)组成平面直角坐标系的四个要素:①在同一平面内;②两条数轴;③互相垂直;④有公共原点.(2)两个规定:①正方向的规定:横轴取向右为正方向,纵轴取向上为正方向;②两条数轴单位长度规定:一般情况下,横轴与纵轴单位长度相同,为了实际需要有时横轴与纵轴单位长度可以不同.
3.坐标平面内点的坐标的符号特征(填“+”或“-”):
点的位置 横坐标的符号 纵坐标的符号
第一象限
第二象限
第三象限
第四象限
4.特殊点的坐标性质:
(1)平行于坐标轴直线上的点的坐标:平行于x轴的直线上的各点的________相同,_______不同;平行于y轴的直线上的各点的_________相同,__________不同;
(2)点P(x,y)在第一、三象限的角平分线上,则 ,P(x,y)在第二、四象限的角平分线上,则 ;
(3)对称点的坐标:点P(a,b)关于x轴对称的点为_________,点P(a,b)关于y轴对称的点为__________;
(4)点到两轴的距离的意义:点P(x,y)到x轴的距离为_____,到y轴的距离为____;
(5)点的坐标与图形平移的关系:一个图形在平面直角坐标系中进行平移,其坐标就要发生相应的变化,可以简单地理解为:左、右平移纵坐标 ,横坐标 ,变化规律是 ,上下平移横坐标 ,纵坐标 ,变化规律是 .
5.用坐标表示地理位置的一般过程:
(1) ;
(2) ;
(3) .
(学生独立思考后与同伴交流各自的答案,学生代表发言,教师纠正学生出现的问题.)
评析:复习时以点的坐标特征为主线,把全章知识系统化,条理化,全面化,以便于应用,同时也培养了学生的归纳概括能力.
三、运用知识,进行基础训练
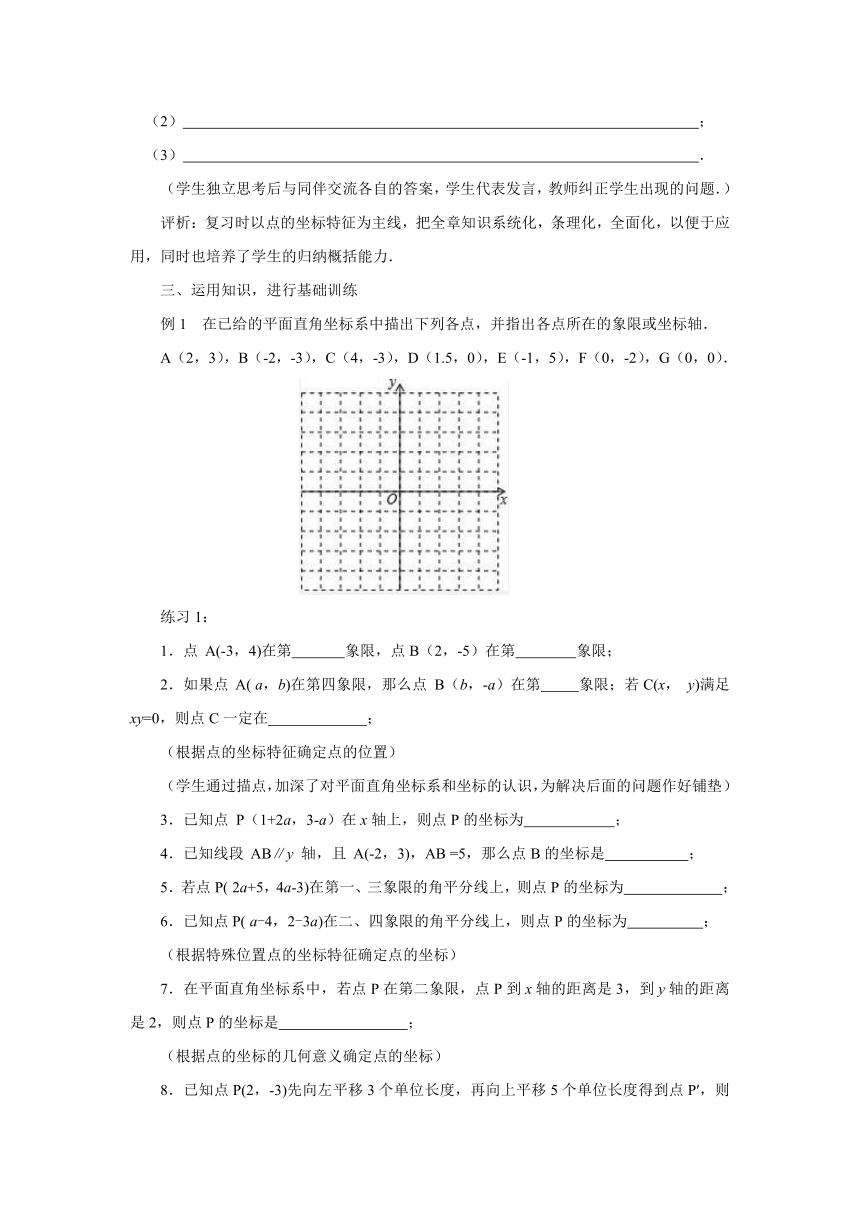
例1 在已给的平面直角坐标系中描出下列各点,并指出各点所在的象限或坐标轴.
A(2,3),B(-2,-3),C(4,-3),D(1.5,0),E(-1,5),F(0,-2),G(0,0).
练习1:
1.点 A(-3,4)在第 象限,点B(2,-5)在第 象限;
2.如果点 A( a,b)在第四象限,那么点 B(b,-a)在第 象限;若C(x, y)满足 xy=0,则点C一定在 ;
(根据点的坐标特征确定点的位置)
(学生通过描点,加深了对平面直角坐标系和坐标的认识,为解决后面的问题作好铺垫)
3.已知点 P(1+2a,3-a)在x轴上,则点P的坐标为 ;
4.已知线段 AB∥y 轴,且 A(-2,3),AB =5,那么点B的坐标是 ;
5.若点P( 2a+5,4a-3)在第一、三象限的角平分线上,则点P的坐标为 ;
6.已知点P( a-4,2-3a)在二、四象限的角平分线上,则点P的坐标为 ;
(根据特殊位置点的坐标特征确定点的坐标)
7.在平面直角坐标系中,若点P在第二象限,点P到x轴的距离是3,到y轴的距离是2,则点P的坐标是 ;
(根据点的坐标的几何意义确定点的坐标)
8.已知点P(2,-3)先向左平移3个单位长度,再向上平移5个单位长度得到点P′,则点P′坐标为 ;(根据点的平移变换与坐标变化规律确定点的坐标)
9.点P(3,-2)关于y 轴对称点的坐标是 .(根据对称点坐标的规律确定点的坐标)
评析:这些题型不仅对所学知识能进一步理解和应用,而且也提高了学生用数学知识解决问题的能力.
例2 如图是某市部分平面简图(图中小正方形的边长代表100 m长),请建立适当的平面直角坐标系,并写出各地的坐标.
(学生在自己设计的活动中体验怎样建立平面直角坐标系,训练学生数学表达能力,也给学生极大的创造空间,有利于学生个性发展)
四、拓宽知识,实现知识迁移
师:平面直角坐标系是建立图形和数量关系的桥梁,反映了数学中重要的思想方法——数形结合,下面我们以图形面积为例说明怎样用数形结合思想、转化思想解决有关问题.
例3 在平面直角坐标系中,△ABC的顶点都在网格点上.
(1)平移△ABC,使得点C与坐标原点O重合,请画出平移后的△A′B′C′;
(2)写出A、B两点对应点A′、B′的坐标;
(3)求△A′B′C′的面积.
(学生自己动手画图,作适当的辅助线,将所求图形的面积转化为规则图形的面积差来求,然后同伴相互交流)
评析:学生在做数学的过程中掌握了一些数学思想方法,积累了数学解题经验,感受到了数学的应用价值.
练习2
1.在平面直角坐标系中,点P(m2+1,-4)在 象限.
2.已知点A(a,-5),B(8,b),根据下列要求,确定a,b的值:
(1)A,B两点关于y轴对称;
(2)A,B两点关于原点对称;
(3)AB∥x轴;
(4)A,B两点在第一,三象限的平分线上.
3.在边长为1的小正方形网格中,△AOB的顶点均在格点上,
(1)B点关于y轴的对称点坐标为 ;
(2)将△AOB向左平移3个单位长度得到△A1O1B1,请画出△A1O1B1;
(3)在(2)的条件下,A1的坐标为 .
4.如图,方格纸中每个小方格都是长为1个单位的正方形,若学校位置坐标为A(2,1),图书馆位置坐标为B(﹣1,﹣2),解答以下问题:
(1)在图中试找出坐标系的原点,并建立直角坐标系;
(2)若体育馆位置坐标为C(1,﹣3),请在坐标系中标出体育馆的位置;
(3)顺次连接学校、图书馆、体育馆,得到△ABC,求△ABC的面积.
五、师生小结,概括本章内容
通过本节复习课,你对本章知识是否有了更深的认识呢?谈谈你的体会.
(通过学生自己总结,加强学生对复习课的认识和学习方法的掌握)
六、布置作业,拓展思维空间
1.书本P84第1,2,4题;
2.请你绘制一幅学校平面分布图,并用坐标表示.(强化用坐标表示地理位置的实际应用).
教学目标:
1.能准确画出平面直角坐标系,由点的位置写出坐标,由点的坐标确定点的位置.掌握特殊位置点的坐标特征,并能用坐标表示平移变换.
2.会建立适当的平面直角坐标系,用坐标表示地理位置.
3.通过观察、尝试、交流,提高学生数形结合思想,培养学生归纳,整理所学知识和应用数学的意识.
教学重点:
1.准确确定平面内点的位置和坐标,并能进行综合应用.
2.根据实际问题建立适当的平面直角坐标系,并解决实际问题
教学难点:
1.正确运用坐标特征解决实际问题.
2.平面直角坐标系的实际应用.
教学方法:启发、讨论、交流.
教学过程:
1、 创设情景,导入新课
这是一张某市旅游景点示意图,我们以中心广场所在水平线为横轴,以中心广场所在铅垂线为纵轴建立平面直角坐标系,你们能说出各景点的坐标吗?
平面直角坐标系是确定平面内点的坐标的重要工具,用它可以解决很多实际问题,本节课我们大家一起来复面直角坐标系”这一章.(由一个具体实例引出课题,可激发学生的兴趣,创造积极的求知氛围)
二、师生互动,构建知识框架
1.有序数对:有序数对是指______的两个数组成的数对,它的表示形式是(a,b).
2.平面直角坐标系的意义:在平面内,两条具有 、并且______的数轴所构成的图形叫做平面直角坐标系,其中水平的数轴叫做______或_______,取向______方向为正方向,竖直的数轴叫做______或_______,取向______方向为正方向,横轴与纵轴的交点叫做平面直角坐标系的______,平面直角坐标系的两条数轴把坐标平面分成四个象限,这两条数轴的正方向的所夹的象限叫做第______象限,其它三个象限按逆时针方向依次叫做第______、______、______象限,坐标轴不属于任何象限.
注意:(1)组成平面直角坐标系的四个要素:①在同一平面内;②两条数轴;③互相垂直;④有公共原点.(2)两个规定:①正方向的规定:横轴取向右为正方向,纵轴取向上为正方向;②两条数轴单位长度规定:一般情况下,横轴与纵轴单位长度相同,为了实际需要有时横轴与纵轴单位长度可以不同.
3.坐标平面内点的坐标的符号特征(填“+”或“-”):
点的位置 横坐标的符号 纵坐标的符号
第一象限
第二象限
第三象限
第四象限
4.特殊点的坐标性质:
(1)平行于坐标轴直线上的点的坐标:平行于x轴的直线上的各点的________相同,_______不同;平行于y轴的直线上的各点的_________相同,__________不同;
(2)点P(x,y)在第一、三象限的角平分线上,则 ,P(x,y)在第二、四象限的角平分线上,则 ;
(3)对称点的坐标:点P(a,b)关于x轴对称的点为_________,点P(a,b)关于y轴对称的点为__________;
(4)点到两轴的距离的意义:点P(x,y)到x轴的距离为_____,到y轴的距离为____;
(5)点的坐标与图形平移的关系:一个图形在平面直角坐标系中进行平移,其坐标就要发生相应的变化,可以简单地理解为:左、右平移纵坐标 ,横坐标 ,变化规律是 ,上下平移横坐标 ,纵坐标 ,变化规律是 .
5.用坐标表示地理位置的一般过程:
(1) ;
(2) ;
(3) .
(学生独立思考后与同伴交流各自的答案,学生代表发言,教师纠正学生出现的问题.)
评析:复习时以点的坐标特征为主线,把全章知识系统化,条理化,全面化,以便于应用,同时也培养了学生的归纳概括能力.
三、运用知识,进行基础训练
例1 在已给的平面直角坐标系中描出下列各点,并指出各点所在的象限或坐标轴.
A(2,3),B(-2,-3),C(4,-3),D(1.5,0),E(-1,5),F(0,-2),G(0,0).
练习1:
1.点 A(-3,4)在第 象限,点B(2,-5)在第 象限;
2.如果点 A( a,b)在第四象限,那么点 B(b,-a)在第 象限;若C(x, y)满足 xy=0,则点C一定在 ;
(根据点的坐标特征确定点的位置)
(学生通过描点,加深了对平面直角坐标系和坐标的认识,为解决后面的问题作好铺垫)
3.已知点 P(1+2a,3-a)在x轴上,则点P的坐标为 ;
4.已知线段 AB∥y 轴,且 A(-2,3),AB =5,那么点B的坐标是 ;
5.若点P( 2a+5,4a-3)在第一、三象限的角平分线上,则点P的坐标为 ;
6.已知点P( a-4,2-3a)在二、四象限的角平分线上,则点P的坐标为 ;
(根据特殊位置点的坐标特征确定点的坐标)
7.在平面直角坐标系中,若点P在第二象限,点P到x轴的距离是3,到y轴的距离是2,则点P的坐标是 ;
(根据点的坐标的几何意义确定点的坐标)
8.已知点P(2,-3)先向左平移3个单位长度,再向上平移5个单位长度得到点P′,则点P′坐标为 ;(根据点的平移变换与坐标变化规律确定点的坐标)
9.点P(3,-2)关于y 轴对称点的坐标是 .(根据对称点坐标的规律确定点的坐标)
评析:这些题型不仅对所学知识能进一步理解和应用,而且也提高了学生用数学知识解决问题的能力.
例2 如图是某市部分平面简图(图中小正方形的边长代表100 m长),请建立适当的平面直角坐标系,并写出各地的坐标.
(学生在自己设计的活动中体验怎样建立平面直角坐标系,训练学生数学表达能力,也给学生极大的创造空间,有利于学生个性发展)
四、拓宽知识,实现知识迁移
师:平面直角坐标系是建立图形和数量关系的桥梁,反映了数学中重要的思想方法——数形结合,下面我们以图形面积为例说明怎样用数形结合思想、转化思想解决有关问题.
例3 在平面直角坐标系中,△ABC的顶点都在网格点上.
(1)平移△ABC,使得点C与坐标原点O重合,请画出平移后的△A′B′C′;
(2)写出A、B两点对应点A′、B′的坐标;
(3)求△A′B′C′的面积.
(学生自己动手画图,作适当的辅助线,将所求图形的面积转化为规则图形的面积差来求,然后同伴相互交流)
评析:学生在做数学的过程中掌握了一些数学思想方法,积累了数学解题经验,感受到了数学的应用价值.
练习2
1.在平面直角坐标系中,点P(m2+1,-4)在 象限.
2.已知点A(a,-5),B(8,b),根据下列要求,确定a,b的值:
(1)A,B两点关于y轴对称;
(2)A,B两点关于原点对称;
(3)AB∥x轴;
(4)A,B两点在第一,三象限的平分线上.
3.在边长为1的小正方形网格中,△AOB的顶点均在格点上,
(1)B点关于y轴的对称点坐标为 ;
(2)将△AOB向左平移3个单位长度得到△A1O1B1,请画出△A1O1B1;
(3)在(2)的条件下,A1的坐标为 .
4.如图,方格纸中每个小方格都是长为1个单位的正方形,若学校位置坐标为A(2,1),图书馆位置坐标为B(﹣1,﹣2),解答以下问题:
(1)在图中试找出坐标系的原点,并建立直角坐标系;
(2)若体育馆位置坐标为C(1,﹣3),请在坐标系中标出体育馆的位置;
(3)顺次连接学校、图书馆、体育馆,得到△ABC,求△ABC的面积.
五、师生小结,概括本章内容
通过本节复习课,你对本章知识是否有了更深的认识呢?谈谈你的体会.
(通过学生自己总结,加强学生对复习课的认识和学习方法的掌握)
六、布置作业,拓展思维空间
1.书本P84第1,2,4题;
2.请你绘制一幅学校平面分布图,并用坐标表示.(强化用坐标表示地理位置的实际应用).
