鲁教版(五四制)数学六年级上册 探寻神奇的幻方 课件(共23张PPT)
文档属性
| 名称 | 鲁教版(五四制)数学六年级上册 探寻神奇的幻方 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:52:04 | ||
图片预览





文档简介
(共23张PPT)
课前预习
1.将1——9九个数字填写在3×3的方格中,使得每个横行、每个竖列和每条对角线上的三个数之和都相等。
2.查阅有关幻方的资料,了解幻方的起源。
探寻神奇的幻方
鲁教版五·四学制六年级上——综合与实践
一、展示成果,初识幻方
1.请展示自己完成的预习作业,并介绍自己填写方格的体会及所用的时间。
2.说一说你所了解到的幻方。
【预习作业】将1——9九个数字填写在3×3的方格中,使得每个横行、每个竖列和每条对角线上的三个数之和都相等。
关于幻方
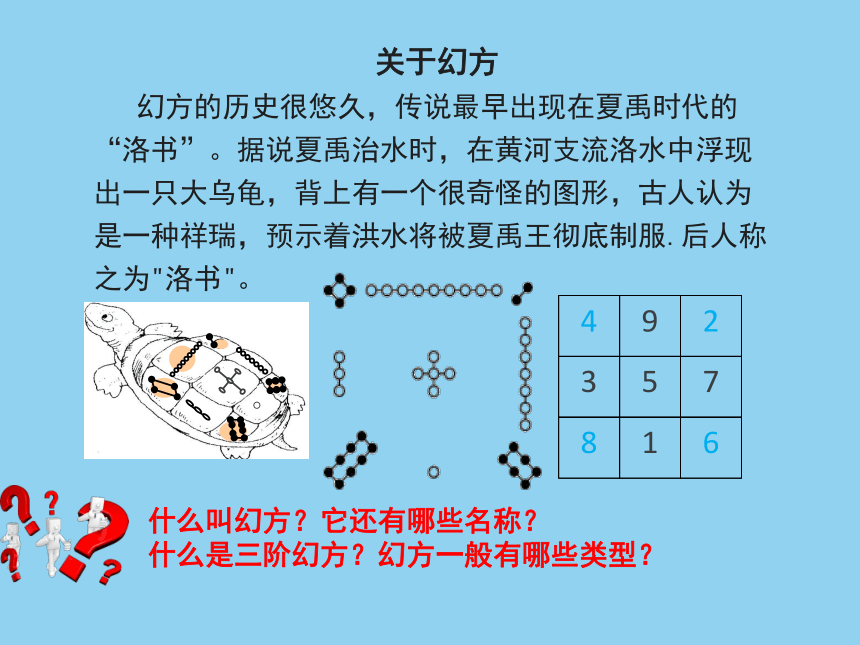
幻方的历史很悠久,传说最早出现在夏禹时代的“洛书”。据说夏禹治水时,在黄河支流洛水中浮现出一只大乌龟,背上有一个很奇怪的图形,古人认为是一种祥瑞,预示着洪水将被夏禹王彻底制服.后人称之为"洛书"。
2
9
4
3
5
7
8
1
6
什么叫幻方?它还有哪些名称?
什么是三阶幻方?幻方一般有哪些类型?
幻方:是一个方形的表格,其中每个格中都填入了各不相同的整数,从而使每一行、每一列以及每条对角线上的数字之和相等(又称为九宫格、纵横图、奇方或方阵、魔阵等)这个和称为幻和。
n阶幻方:由1到n2,这n2个自然数组成的幻方称为n阶幻方或n阶纵横图。
幻方的一般分类:
按照纵横各有数字的个数,可以分为:
三阶幻方、四阶幻方、五阶幻方、六阶幻方… …
按照纵横数字数量奇偶的不同,可以分为:
奇阶幻方、偶阶幻方。
你想了解更多有关幻方的故事吗?
你知道三阶幻方有哪些特点吗?
如何能在最短的时间里面构建三阶幻方?
如果换9个数字,你还能很快地构建广义的三阶幻方吗?
2
9
4
3
5
7
8
1
6
二、合作探索,研究幻方
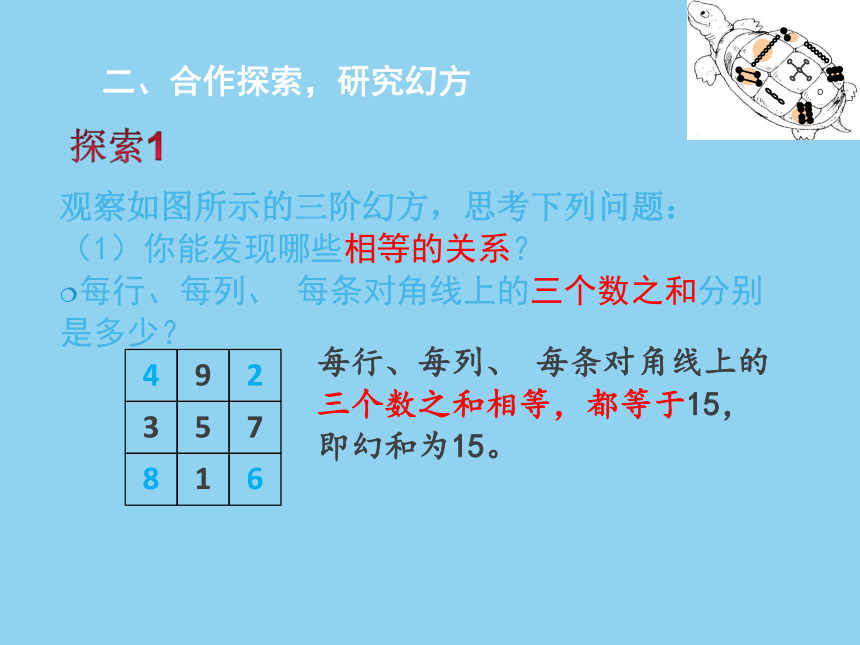
观察如图所示的三阶幻方,思考下列问题:
(1)你能发现哪些相等的关系?
每行、每列、 每条对角线上的三个数之和分别是多少?
2
9
4
3
5
7
8
1
6
每行、每列、 每条对角线上的三个数之和相等,都等于15,即幻和为15。
探索1
二、合作探索,研究幻方
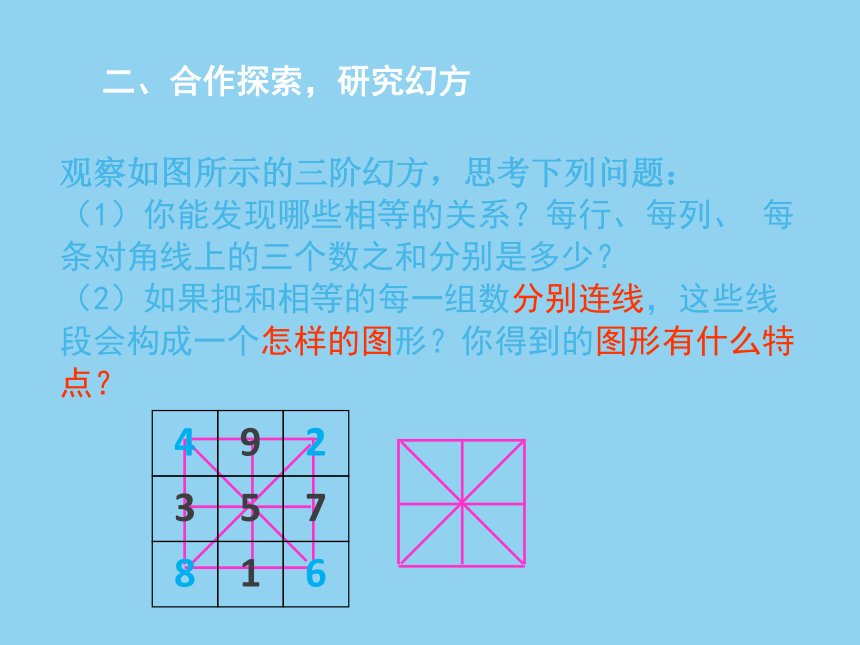
观察如图所示的三阶幻方,思考下列问题:
(1)你能发现哪些相等的关系?每行、每列、 每条对角线上的三个数之和分别是多少?
(2)如果把和相等的每一组数分别连线,这些线段会构成一个怎样的图形?你得到的图形有什么特点?
2
9
4
3
5
7
8
1
6
二、合作探索,研究幻方
(3)你能否改变如图所示幻方中数字的位置,使它们仍然满足你发现的那些相等关系?(先独立思考,再小组进行交流)
2
9
4
3
5
7
8
1
6
二、合作探索,研究幻方
(3)你能否改变如图所示幻方中数字的位置,使它们仍然满足你发现的那些相等关系?
2
9
4
3
5
7
8
1
6
4
6
2
8
9
1
3
7
5
6
4
8
2
1
9
7
3
5
4
6
2
8
9
1
3
7
5
4
6
2
8
9
1
3
7
5
4
6
2
8
9
1
3
7
5
4
6
2
8
9
1
3
7
5
2
8
6
4
7
3
9
1
5
二、合作探索,研究幻方
(4)在你构造的幻方中,最核心的位置是什么?在这个位置上出现的数是几?有没有“成对”出现的数?
2
9
4
3
5
7
8
1
6
为什么5必须放在中间
为什么会有“成对”出现的数呢
先独立思考,再组内交流,说说你的理由。
最核心的位置是正中间,这个位置出现的数是5;
2
9
4
3
5
7
8
1
6
成对出现的数为:4与6,9与1,2与8,3与7。
2
9
4
3
5
7
8
1
6
c
b
a
d
e
f
g
h
i
如图,将九个数字分别用a,b,c,d,e,f,g,h,i来表示,
∵1-9这九个数的和为45
∴每行、每列、每条对角线上的三个数之和都是15,
即:a+e+i=15,
c+e+g=15,
b+e+h=15,
三式相加得(a+b+c+i+g+h)+3e=45,
又∵ a+b+c=15, i+g+h=15,
∴ e=5
二、合作探索,研究幻方
(5)在如图所示的三阶幻方中,中心方格中的数5与每行、每列和每条对角线上的三个数之和之间分别有什么关系?
(6)你还有什么新的发现?
2
9
4
3
5
7
8
1
6
每行、每列、每条对角线上的三个数之和都是中心数的3倍。
3个数的和
为
6
二、合作探索,研究幻方
在图中所示的两个广义的三阶幻方中分别给出了3个数,你能将其余六个数填上吗?
想一想,学以致用
-1
4
3
-5
-6
-11
3个数的和
为
6
3个数的和=6
2
中心数=6÷3
3个数的和=6
0
5
3个数的和
为
6
6
-2
令右下角的数为x,
则-5+(-11)=2x
解得 x=-8
x
-8
∵-6+(-8)=2×中心数
∴ 中心数=-7
-7
∴可得幻和为-21
-9
-10
-3
-4
3个数的和=6
1
探索2
三、学以致用,制作幻方
(1)用2,3,4,5,6,7,8,9,10这九个数构造一个广义的三阶幻方;
(2)用2,4,6,8,10,12,14,16,18这九个数构造一个广义的三阶幻方;
(3)用-8,-6,-4,-2,0,2,4,6,8这九个数构造一个广义的三阶幻方;
2
9
4
3
5
7
8
1
6
探索3
三、学以致用,制作幻方
说一说,你是用什么方法制作幻方的?
探索3
四、梳理小结,共谈体会
请从下列关键词中选出一个或是几个,谈一谈你对这节课的收获与感受。
我了解了 我学会了 我掌握了 我欣赏 我希望 …… 知识
方法
题型
某某同学
自己
……
五、课后作业,拓展延伸
1.(必做题)在下列各图的空格里,填上合适的数,使横行、竖列及两条对角线上三个数的和都相等.
8
4
2
第1题
9
2
10
五、课后作业,拓展延伸
2. (必做题)利用一个3×3的方框在日历图上任意套出9个数,这9个数能否构造一个广义的三阶幻方?为什么?并思考怎样的9个数可以构造三阶幻方?
第2题
日 一 二 三 四 五 六
1 2 3 4 5 6 7
8 9 10 11 12 13 14
15 16 17 18 19 20 21
22 23 24 25 26 27 28
29 30
五、课后作业,拓展延伸
3.(选做题)自行选取一组数构造一个三阶幻方,使得每行、每列和每条对角线上的三个数之和都等于60.
第3题
祝福同学们, 通过自己的探索与努力, 拥有幻方般美妙的人生!
综合与实践:——探寻神奇的幻方
二、合作探索,研究幻方
新的发现
2
9
4
3
5
7
8
1
6
1+7=4×2
1+3=2×2
3+9=6×2
7+9=8×2
用“奇偶试验法”填写三阶幻方
幻和=15 (奇数)
奇数+奇数+奇数=奇数
偶数+偶数+奇数=奇数
2
9
4
3
5
7
8
1
6
偶数
奇数
偶数
奇数
5
奇数
偶数
奇数
偶数
奇数
偶数
奇数
偶数
5
偶数
奇数
偶数
奇数
×
课前预习
1.将1——9九个数字填写在3×3的方格中,使得每个横行、每个竖列和每条对角线上的三个数之和都相等。
2.查阅有关幻方的资料,了解幻方的起源。
探寻神奇的幻方
鲁教版五·四学制六年级上——综合与实践
一、展示成果,初识幻方
1.请展示自己完成的预习作业,并介绍自己填写方格的体会及所用的时间。
2.说一说你所了解到的幻方。
【预习作业】将1——9九个数字填写在3×3的方格中,使得每个横行、每个竖列和每条对角线上的三个数之和都相等。
关于幻方
幻方的历史很悠久,传说最早出现在夏禹时代的“洛书”。据说夏禹治水时,在黄河支流洛水中浮现出一只大乌龟,背上有一个很奇怪的图形,古人认为是一种祥瑞,预示着洪水将被夏禹王彻底制服.后人称之为"洛书"。
2
9
4
3
5
7
8
1
6
什么叫幻方?它还有哪些名称?
什么是三阶幻方?幻方一般有哪些类型?
幻方:是一个方形的表格,其中每个格中都填入了各不相同的整数,从而使每一行、每一列以及每条对角线上的数字之和相等(又称为九宫格、纵横图、奇方或方阵、魔阵等)这个和称为幻和。
n阶幻方:由1到n2,这n2个自然数组成的幻方称为n阶幻方或n阶纵横图。
幻方的一般分类:
按照纵横各有数字的个数,可以分为:
三阶幻方、四阶幻方、五阶幻方、六阶幻方… …
按照纵横数字数量奇偶的不同,可以分为:
奇阶幻方、偶阶幻方。
你想了解更多有关幻方的故事吗?
你知道三阶幻方有哪些特点吗?
如何能在最短的时间里面构建三阶幻方?
如果换9个数字,你还能很快地构建广义的三阶幻方吗?
2
9
4
3
5
7
8
1
6
二、合作探索,研究幻方
观察如图所示的三阶幻方,思考下列问题:
(1)你能发现哪些相等的关系?
每行、每列、 每条对角线上的三个数之和分别是多少?
2
9
4
3
5
7
8
1
6
每行、每列、 每条对角线上的三个数之和相等,都等于15,即幻和为15。
探索1
二、合作探索,研究幻方
观察如图所示的三阶幻方,思考下列问题:
(1)你能发现哪些相等的关系?每行、每列、 每条对角线上的三个数之和分别是多少?
(2)如果把和相等的每一组数分别连线,这些线段会构成一个怎样的图形?你得到的图形有什么特点?
2
9
4
3
5
7
8
1
6
二、合作探索,研究幻方
(3)你能否改变如图所示幻方中数字的位置,使它们仍然满足你发现的那些相等关系?(先独立思考,再小组进行交流)
2
9
4
3
5
7
8
1
6
二、合作探索,研究幻方
(3)你能否改变如图所示幻方中数字的位置,使它们仍然满足你发现的那些相等关系?
2
9
4
3
5
7
8
1
6
4
6
2
8
9
1
3
7
5
6
4
8
2
1
9
7
3
5
4
6
2
8
9
1
3
7
5
4
6
2
8
9
1
3
7
5
4
6
2
8
9
1
3
7
5
4
6
2
8
9
1
3
7
5
2
8
6
4
7
3
9
1
5
二、合作探索,研究幻方
(4)在你构造的幻方中,最核心的位置是什么?在这个位置上出现的数是几?有没有“成对”出现的数?
2
9
4
3
5
7
8
1
6
为什么5必须放在中间
为什么会有“成对”出现的数呢
先独立思考,再组内交流,说说你的理由。
最核心的位置是正中间,这个位置出现的数是5;
2
9
4
3
5
7
8
1
6
成对出现的数为:4与6,9与1,2与8,3与7。
2
9
4
3
5
7
8
1
6
c
b
a
d
e
f
g
h
i
如图,将九个数字分别用a,b,c,d,e,f,g,h,i来表示,
∵1-9这九个数的和为45
∴每行、每列、每条对角线上的三个数之和都是15,
即:a+e+i=15,
c+e+g=15,
b+e+h=15,
三式相加得(a+b+c+i+g+h)+3e=45,
又∵ a+b+c=15, i+g+h=15,
∴ e=5
二、合作探索,研究幻方
(5)在如图所示的三阶幻方中,中心方格中的数5与每行、每列和每条对角线上的三个数之和之间分别有什么关系?
(6)你还有什么新的发现?
2
9
4
3
5
7
8
1
6
每行、每列、每条对角线上的三个数之和都是中心数的3倍。
3个数的和
为
6
二、合作探索,研究幻方
在图中所示的两个广义的三阶幻方中分别给出了3个数,你能将其余六个数填上吗?
想一想,学以致用
-1
4
3
-5
-6
-11
3个数的和
为
6
3个数的和=6
2
中心数=6÷3
3个数的和=6
0
5
3个数的和
为
6
6
-2
令右下角的数为x,
则-5+(-11)=2x
解得 x=-8
x
-8
∵-6+(-8)=2×中心数
∴ 中心数=-7
-7
∴可得幻和为-21
-9
-10
-3
-4
3个数的和=6
1
探索2
三、学以致用,制作幻方
(1)用2,3,4,5,6,7,8,9,10这九个数构造一个广义的三阶幻方;
(2)用2,4,6,8,10,12,14,16,18这九个数构造一个广义的三阶幻方;
(3)用-8,-6,-4,-2,0,2,4,6,8这九个数构造一个广义的三阶幻方;
2
9
4
3
5
7
8
1
6
探索3
三、学以致用,制作幻方
说一说,你是用什么方法制作幻方的?
探索3
四、梳理小结,共谈体会
请从下列关键词中选出一个或是几个,谈一谈你对这节课的收获与感受。
我了解了 我学会了 我掌握了 我欣赏 我希望 …… 知识
方法
题型
某某同学
自己
……
五、课后作业,拓展延伸
1.(必做题)在下列各图的空格里,填上合适的数,使横行、竖列及两条对角线上三个数的和都相等.
8
4
2
第1题
9
2
10
五、课后作业,拓展延伸
2. (必做题)利用一个3×3的方框在日历图上任意套出9个数,这9个数能否构造一个广义的三阶幻方?为什么?并思考怎样的9个数可以构造三阶幻方?
第2题
日 一 二 三 四 五 六
1 2 3 4 5 6 7
8 9 10 11 12 13 14
15 16 17 18 19 20 21
22 23 24 25 26 27 28
29 30
五、课后作业,拓展延伸
3.(选做题)自行选取一组数构造一个三阶幻方,使得每行、每列和每条对角线上的三个数之和都等于60.
第3题
祝福同学们, 通过自己的探索与努力, 拥有幻方般美妙的人生!
综合与实践:——探寻神奇的幻方
二、合作探索,研究幻方
新的发现
2
9
4
3
5
7
8
1
6
1+7=4×2
1+3=2×2
3+9=6×2
7+9=8×2
用“奇偶试验法”填写三阶幻方
幻和=15 (奇数)
奇数+奇数+奇数=奇数
偶数+偶数+奇数=奇数
2
9
4
3
5
7
8
1
6
偶数
奇数
偶数
奇数
5
奇数
偶数
奇数
偶数
奇数
偶数
奇数
偶数
5
偶数
奇数
偶数
奇数
×
