人教版八年级数学下册19.2一次函数的应用——面积问题教学设计
文档属性
| 名称 | 人教版八年级数学下册19.2一次函数的应用——面积问题教学设计 |  | |
| 格式 | doc | ||
| 文件大小 | 147.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 10:08:32 | ||
图片预览

文档简介
课题名称 《一次函数的应用——面积问题》
教学目标 知识与技能 能利用点的坐标求三角形的面积,能利用面积求点的坐标。
过程与方法 通过动点的坐标与三角形的面积的关系的探究,使学生理解动点的坐标与三角形的面积的联系规律,体会数形结合思想。
情感、态度与价值观 培养学生主动探究,合作交流的意识,激发学生学习数学的热情,体验学数学的乐趣。
教学重、难点 重点 根据函数表达式求三角形的面积,会根据面积求点坐标。
难点 探究理解动点的坐标与三角形面积的关系。
教法选择 1、遵循以学生为主体,练习为主线,思维为中心,采用并发展了兴趣教学法,本人作为学生的组织者、引导者、合作者。2、让学生在老师的指导下,进行探究性学习,合作交流,让学生自己发现问题,并逐步能解决问题。
学法指导 根据学生是课堂主体的教学要求,本节课从学生的角度出发,采用以“自主参与,合作探究”的学法。
《一次函数的应用——面积问题》教学设计
教学过程 教师活动 学生活动 设计意图
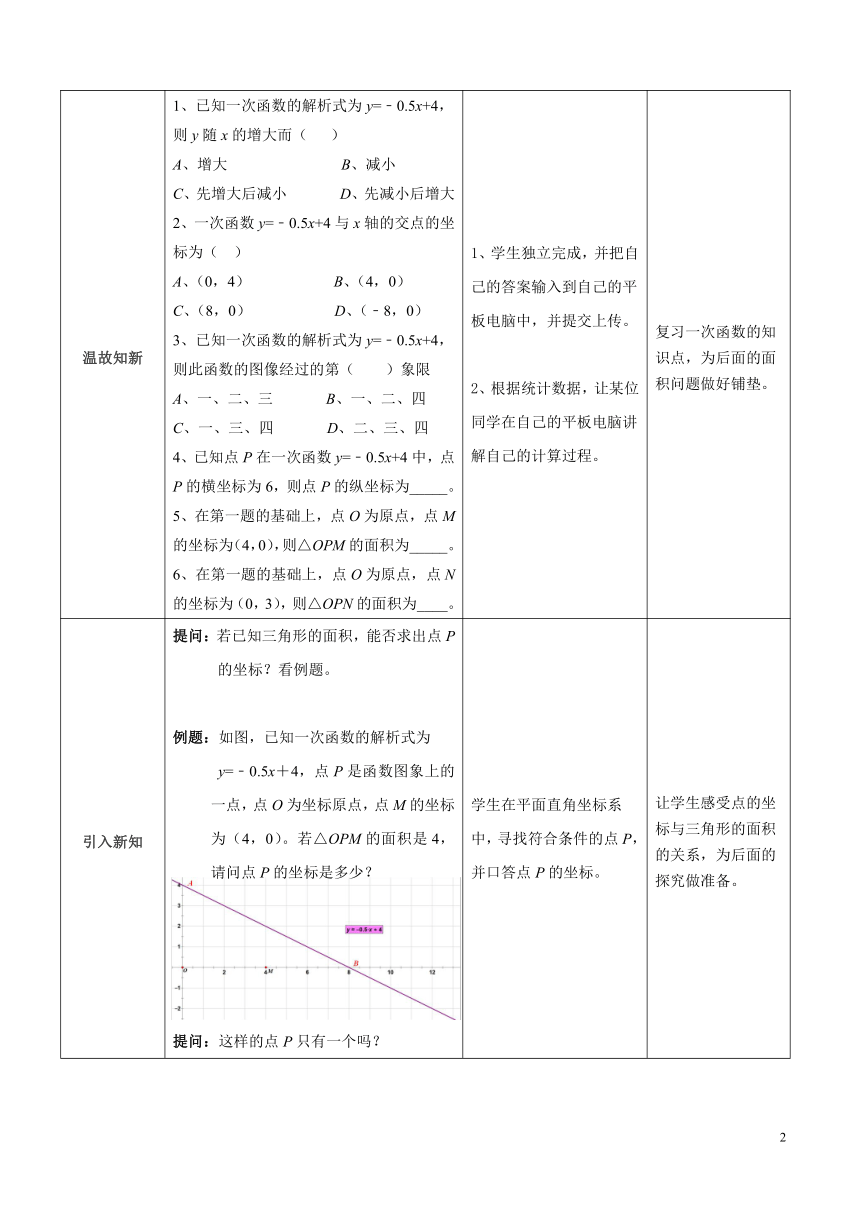
温故知新 1、已知一次函数的解析式为y=﹣0.5x+4,则y随x的增大而( )A、增大 B、减小 C、先增大后减小 D、先减小后增大2、一次函数y=﹣0.5x+4与x轴的交点的坐标为( )A、(0,4) B、(4,0) C、(8,0) D、(﹣8,0)3、已知一次函数的解析式为y=﹣0.5x+4,则此函数的图像经过的第( )象限A、一、二、三 B、一、二、四 C、一、三、四 D、二、三、四4、已知点P在一次函数y=﹣0.5x+4中,点P的横坐标为6,则点P的纵坐标为_____。5、在第一题的基础上,点O为原点,点M的坐标为(4,0),则△OPM的面积为_____。6、在第一题的基础上,点O为原点,点N的坐标为(0,3),则△OPN的面积为____。 1、学生独立完成,并把自己的答案输入到自己的平板电脑中,并提交上传。2、根据统计数据,让某位同学在自己的平板电脑讲解自己的计算过程。 复习一次函数的知识点,为后面的面积问题做好铺垫。
引入新知 提问:若已知三角形的面积,能否求出点P的坐标?看例题。例题:如图,已知一次函数的解析式为y=﹣0.5x+4,点P是函数图象上的一点,点O为坐标原点,点M的坐标为(4,0)。若△OPM的面积是4,请问点P的坐标是多少?提问:这样的点P只有一个吗? 学生在平面直角坐标系中,寻找符合条件的点P,并口答点P的坐标。 让学生感受点的坐标与三角形的面积的关系,为后面的探究做准备。
探究规律 提问:点P的位置改变,△OPM的面积也在改变,那么如果点P是一个动点,那么△OPM的面积又该如何表示呢?例题:(2)若点P的坐标为(x,y),则△POM的面积S怎么表示呢? 学生观察点的位置与三角形的面积,并通过观察动态视频,小组讨论,总结点P的坐标与△POM的面积的关系。 学生通过观察体会,小组讨论,探究出点的坐标与三角形的面积关系,,培养学生的探究能力和归纳能力。
规律应用 提问:我们归纳点P的坐标与△POM的面积的关系,能否根据关系式,求出符合条件的点P的坐标。例题:(3)请问:P的坐标为多少时,△POM面积等于一次函数的图象与坐标轴围成的三角形面积的一半。 学生根据推导出的关系式,求出点P的坐标,并阐述计算过程。 考察学生对关系式的应用能力。
巩固训练 如图,已知一次函数的解析式为y=﹣0.5x+4,点P是函数图象的一点,点O为坐标原点,点N的坐标为(0,3)。(1)若点P的纵坐标为2时,则△OPN面积为多少?(2)若点P的坐标为(x,y),则△OPN面积为多少?(3)当点P的坐标为多少时,则△OPN面积为一次函数的图象与坐标轴围成的三角形面积的一半 学生根据例题的探究方法,自行推导关系式,并利用关系式求出点的坐标 考察学生对所学知识的应用能力。
总结方法 1、在动点的运动过程中,观察图形的变化情况,需要理解图形在不同位置的情况,才能做好计算推理的过程。2、在变化中找到不变的性质是解决数学“动点”探究题的基本思路,这也是动态几何数学问题中最核心的数学本质。 学生共同总结 让学生体会、理解动点问题的一般解决方法。
作业布置 已知在平面直角坐标系中,点A的坐标为(6,0),另有一动点B的坐标为(x,y),且点B的横纵坐标之和为8,设△OAB的面积为s,求: (1)s与点B的横纵坐标x之间的函数关系式,并写出自变量的取值范围。 (2)当△OAB的面积为20时,求B点的坐标。 学生课后自主完成 让学生对所学的知识点加深巩固。
设计说明
本教学设计力求体现以人为本的教育理念,让学生在经历“问题情境——建立模型——解释应用——延伸课题”的基本过程中,体验知识间的内在联系,感受到数学有用、有趣和数学好玩。
在教学过程中本着活化教材、强化体验、深化应用的原则,从学生认知出发,通过一系列的探究、升华让学生感受一次函数对动点面积的应用,从而明确学习一次函数的意义和作用,凸现数学即生活的新课程理念,渗透“以知生情”的数学文化。在教学活动中,通过学生的自主学习来体现他们的主体地位,而教师是通过对学生参与学习的启发、调整、激励来体现自己的主导作用。
另外,在学生合作学习的同时,始终坚持对学生进行 “学疑结合”、“学思结合”、“学用结合”的学法指导,对学生的主体意识和创新能力的培养有着积极的意义。
教学反思
本节课的设计,力求体现新课程改革的理念,与平板电脑教学进行很好的对接,充分体现出教学信息化的特征,为学生营造宽松、和谐的氛围,让学生学得更主动、更轻松,力求在探索知识的过程中,培养学生的探索能力和创新能力,激发学生学习的积极性。在学生选择解决问题的诸多方法的过程中,不过多地干涉学生的思维,而是通过引导学生自己去探究来选择解决问题的办法。
本节课也存在一些应该深刻的反思和改进的地方。例如在探究活动中有些问题处理的有些仓促,有些问题的指向性有些不需太明确,需要今后加强。另外,今后教学中还应该更多地关注学生的发展和提升。多用幽默和鼓励性的语言激励学生。
总之,本节课着力做到课堂是数学活动的场所,是师生共同成长的基地,是学生张扬自我舞台。
y
PAGE
5
教学目标 知识与技能 能利用点的坐标求三角形的面积,能利用面积求点的坐标。
过程与方法 通过动点的坐标与三角形的面积的关系的探究,使学生理解动点的坐标与三角形的面积的联系规律,体会数形结合思想。
情感、态度与价值观 培养学生主动探究,合作交流的意识,激发学生学习数学的热情,体验学数学的乐趣。
教学重、难点 重点 根据函数表达式求三角形的面积,会根据面积求点坐标。
难点 探究理解动点的坐标与三角形面积的关系。
教法选择 1、遵循以学生为主体,练习为主线,思维为中心,采用并发展了兴趣教学法,本人作为学生的组织者、引导者、合作者。2、让学生在老师的指导下,进行探究性学习,合作交流,让学生自己发现问题,并逐步能解决问题。
学法指导 根据学生是课堂主体的教学要求,本节课从学生的角度出发,采用以“自主参与,合作探究”的学法。
《一次函数的应用——面积问题》教学设计
教学过程 教师活动 学生活动 设计意图
温故知新 1、已知一次函数的解析式为y=﹣0.5x+4,则y随x的增大而( )A、增大 B、减小 C、先增大后减小 D、先减小后增大2、一次函数y=﹣0.5x+4与x轴的交点的坐标为( )A、(0,4) B、(4,0) C、(8,0) D、(﹣8,0)3、已知一次函数的解析式为y=﹣0.5x+4,则此函数的图像经过的第( )象限A、一、二、三 B、一、二、四 C、一、三、四 D、二、三、四4、已知点P在一次函数y=﹣0.5x+4中,点P的横坐标为6,则点P的纵坐标为_____。5、在第一题的基础上,点O为原点,点M的坐标为(4,0),则△OPM的面积为_____。6、在第一题的基础上,点O为原点,点N的坐标为(0,3),则△OPN的面积为____。 1、学生独立完成,并把自己的答案输入到自己的平板电脑中,并提交上传。2、根据统计数据,让某位同学在自己的平板电脑讲解自己的计算过程。 复习一次函数的知识点,为后面的面积问题做好铺垫。
引入新知 提问:若已知三角形的面积,能否求出点P的坐标?看例题。例题:如图,已知一次函数的解析式为y=﹣0.5x+4,点P是函数图象上的一点,点O为坐标原点,点M的坐标为(4,0)。若△OPM的面积是4,请问点P的坐标是多少?提问:这样的点P只有一个吗? 学生在平面直角坐标系中,寻找符合条件的点P,并口答点P的坐标。 让学生感受点的坐标与三角形的面积的关系,为后面的探究做准备。
探究规律 提问:点P的位置改变,△OPM的面积也在改变,那么如果点P是一个动点,那么△OPM的面积又该如何表示呢?例题:(2)若点P的坐标为(x,y),则△POM的面积S怎么表示呢? 学生观察点的位置与三角形的面积,并通过观察动态视频,小组讨论,总结点P的坐标与△POM的面积的关系。 学生通过观察体会,小组讨论,探究出点的坐标与三角形的面积关系,,培养学生的探究能力和归纳能力。
规律应用 提问:我们归纳点P的坐标与△POM的面积的关系,能否根据关系式,求出符合条件的点P的坐标。例题:(3)请问:P的坐标为多少时,△POM面积等于一次函数的图象与坐标轴围成的三角形面积的一半。 学生根据推导出的关系式,求出点P的坐标,并阐述计算过程。 考察学生对关系式的应用能力。
巩固训练 如图,已知一次函数的解析式为y=﹣0.5x+4,点P是函数图象的一点,点O为坐标原点,点N的坐标为(0,3)。(1)若点P的纵坐标为2时,则△OPN面积为多少?(2)若点P的坐标为(x,y),则△OPN面积为多少?(3)当点P的坐标为多少时,则△OPN面积为一次函数的图象与坐标轴围成的三角形面积的一半 学生根据例题的探究方法,自行推导关系式,并利用关系式求出点的坐标 考察学生对所学知识的应用能力。
总结方法 1、在动点的运动过程中,观察图形的变化情况,需要理解图形在不同位置的情况,才能做好计算推理的过程。2、在变化中找到不变的性质是解决数学“动点”探究题的基本思路,这也是动态几何数学问题中最核心的数学本质。 学生共同总结 让学生体会、理解动点问题的一般解决方法。
作业布置 已知在平面直角坐标系中,点A的坐标为(6,0),另有一动点B的坐标为(x,y),且点B的横纵坐标之和为8,设△OAB的面积为s,求: (1)s与点B的横纵坐标x之间的函数关系式,并写出自变量的取值范围。 (2)当△OAB的面积为20时,求B点的坐标。 学生课后自主完成 让学生对所学的知识点加深巩固。
设计说明
本教学设计力求体现以人为本的教育理念,让学生在经历“问题情境——建立模型——解释应用——延伸课题”的基本过程中,体验知识间的内在联系,感受到数学有用、有趣和数学好玩。
在教学过程中本着活化教材、强化体验、深化应用的原则,从学生认知出发,通过一系列的探究、升华让学生感受一次函数对动点面积的应用,从而明确学习一次函数的意义和作用,凸现数学即生活的新课程理念,渗透“以知生情”的数学文化。在教学活动中,通过学生的自主学习来体现他们的主体地位,而教师是通过对学生参与学习的启发、调整、激励来体现自己的主导作用。
另外,在学生合作学习的同时,始终坚持对学生进行 “学疑结合”、“学思结合”、“学用结合”的学法指导,对学生的主体意识和创新能力的培养有着积极的意义。
教学反思
本节课的设计,力求体现新课程改革的理念,与平板电脑教学进行很好的对接,充分体现出教学信息化的特征,为学生营造宽松、和谐的氛围,让学生学得更主动、更轻松,力求在探索知识的过程中,培养学生的探索能力和创新能力,激发学生学习的积极性。在学生选择解决问题的诸多方法的过程中,不过多地干涉学生的思维,而是通过引导学生自己去探究来选择解决问题的办法。
本节课也存在一些应该深刻的反思和改进的地方。例如在探究活动中有些问题处理的有些仓促,有些问题的指向性有些不需太明确,需要今后加强。另外,今后教学中还应该更多地关注学生的发展和提升。多用幽默和鼓励性的语言激励学生。
总之,本节课着力做到课堂是数学活动的场所,是师生共同成长的基地,是学生张扬自我舞台。
y
PAGE
5
