人教版九年级下册 一次函数的复习 教学设计
文档属性
| 名称 | 人教版九年级下册 一次函数的复习 教学设计 |  | |
| 格式 | doc | ||
| 文件大小 | 124.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 10:13:31 | ||
图片预览

文档简介
一次函数的复习
---------初三数学总复习
一、教学目标
(一)考纲要求
1、结合具体情境体会一次函数的意义,根据已知条件确定一次函数表达式.
2、会画一次函数的图象,并会利用待定系数法确定一次函数的解析式,根据一次函数的图象和解析表达式探索并理解其性质(k>0或k<0时,图象的变化情况).
3、理解正比例函数.
4、能根据一次函数的图象求二元一次方程组的近似解.
5、能用一次函数解决实际问题.
(二)过程与方法
1、通过复习进一步发展学生形象思维能力和应用数学的能力
2、发展学生数形结合意识,提高学生观察图象的能力
(三)情感态度价值观
通过复习进一步培养学生良好的学习习惯
(四)教学重难点
1、重点:一次函数的图象与性质.
2、难点:用图象法解二元一次方程组,及利用一次函数的增减性解决实际问题中的最值.
二、学情分析:
学生已经在初二学习过一次函数,现在在初三总复习中再一次复习一次函数,有的学生已经忘记了一次函数的一些知识点,所以有必要系统地给学生复习过一遍一次函数的相关内容。次节课中,学生在原有知识与学习经验对本节课的类比学习奠定扎实的学习基础,在前后知识的类比学习中,学生可以进一步理解函数的知识,体验研究函数的基本思路,促进学生的认知结构的不断的完善,进而发展学生的类比、抽象与概括能力.而这些目标的达成必须是在充分发挥学生的主体作用,给予学生足够的活动、探究、交流、反思的时间与空间,让在学生在类比中学习、在类比中思考的前提下才能完成的.
三、教学内容分析:
一次函数属于《数学课程标准》中“数与代数”领域,是最基本的、最简单的函数,一次函数在中考考察中往往跟反比例函数和二次函数结合在一起,所以复习好一次函数对之后函数的综合题有很大的帮助。
四、教学环节与活动:
(一)知识点回顾和相应题目小练
考点一:正比例函数定义、图像与性质
一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫比例系数.例如:y=5x, y=-2x都是正比例函数
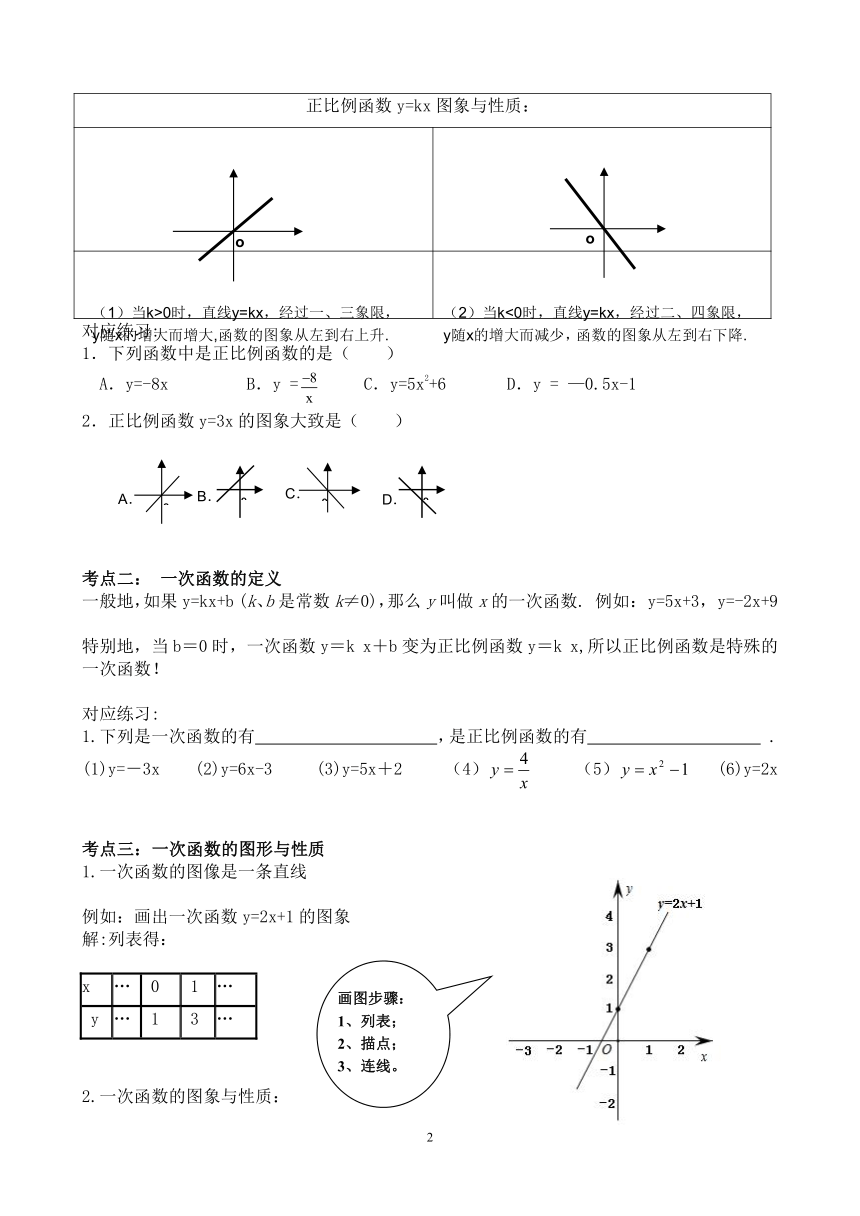
正比例函数y=kx图象与性质:
对应练习:
1.下列函数中是正比例函数的是( )
A.y=-8x B.y = C.y=5x2+6 D.y = —0.5x-1
2.正比例函数y=3x的图象大致是( )
考点二: 一次函数的定义
一般地,如果y=kx+b (k、b是常数k≠0),那么y叫做x的一次函数. 例如: y=5x+3, y=-2x+9
特别地,当b=0时,一次函数y=k x+b变为正比例函数y=k x,所以正比例函数是特殊的一次函数!
对应练习:
1.下列是一次函数的有 ,是正比例函数的有 .
(1)y=-3x (2)y=6x-3 (3)y=5x+2 (4) (5) (6)y=2x
考点三:一次函数的图形与性质
1.一次函数的图像是一条直线
例如:画出一次函数y=2x+1的图象
解:列表得:
x … 0 1 …
y … 1 3 …
2.一次函数的图象与性质:
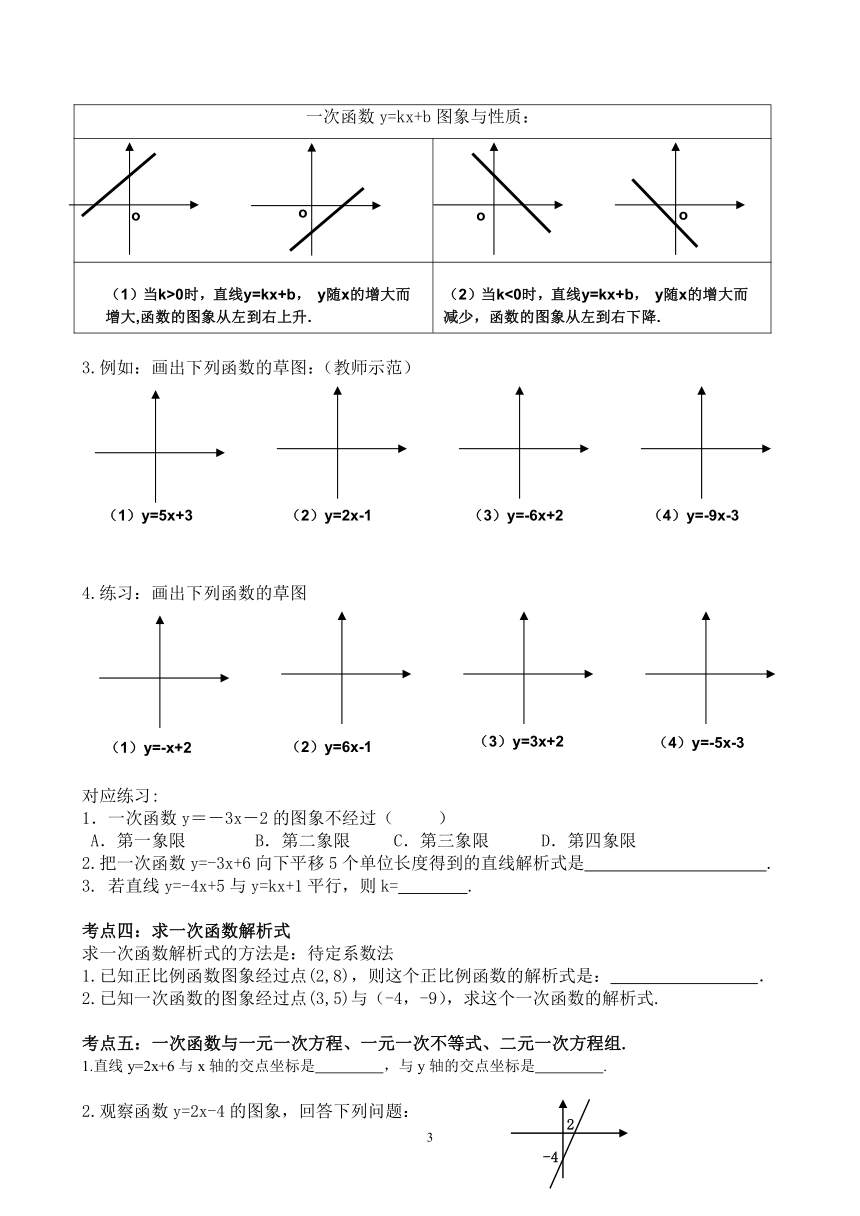
一次函数y=kx+b图象与性质:
3.例如:画出下列函数的草图:(教师示范)
4.练习:画出下列函数的草图
对应练习:
1.一次函数y=-3x-2的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.把一次函数y=-3x+6向下平移5个单位长度得到的直线解析式是 .
3. 若直线y=-4x+5与y=kx+1平行,则k= .
考点四:求一次函数解析式
求一次函数解析式的方法是:待定系数法
1.已知正比例函数图象经过点(2,8),则这个正比例函数的解析式是: .
2.已知一次函数的图象经过点(3,5)与(-4,-9),求这个一次函数的解析式.
考点五:一次函数与一元一次方程、一元一次不等式、二元一次方程组.
1.直线y=2x+6与x轴的交点坐标是 ,与y轴的交点坐标是 .
2.观察函数y=2x-4的图象,回答下列问题:
(1)当x , 2x-4>0?
(2)当x , 2x-4<0
3.一次函数y=-x-3与y=x-3的图象如图所示,则这两个函
数图象的交点坐标是 ,方程组 的解是
考点六:一次函数的应用
1.某市出租车计费方法如图所示,请根据图象回答
下面的问题:
(1)出租车的起步价是 元,在路程 千米内只收起步价.
(2)表示路程s大于3km时,费用y与s之间的函数关系式
是 .
(3)某乘客坐出租车,车费为31元,则他乘车的路程是 千米.
(二)课堂练习:《校本》第24页“基础训练”
基础训练:
1.已知函数y=4x+5,当x=-3时,y=___;当y=5时,x=___.
2. 函数y=xm-8是正比例函数,则m=______,y随x的增大而________.
3.一次函数y=2x-3的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第一象限
4.已知直线y=kx+b中,当x1>x2时,y1>y2,则下列结论中一定正确的是( )
A.k>0 B.k<0 C.b>0 D.b<0
5.将直线y=2x向下平移1个单位后所得图象对应的函数解析式为( )
A.y=2x-1 B.y=2x-2
C.y=2x+1 D.y=2x+2
6.若实数a,b满足ab<0,且a<b,则函数y=ax+b的图象可能是( )
7.如图,一次函数y=﹣x+m的图象和y轴交于点B,与正比例函数y=x图象交于点P (2,n).
(1)求m和n的值;
(2)求△POB的面积.
(三)小结:(引导学生回顾复习的知识点)
1、正比例函数定义、图像与性质
2、一次函数的定义
3、一次函数的图形与性质
4、求一次函数解析式
5、一次函数与一元一次方程、一元一次不等式、二元一次方程组
6、一次函数的应用
(四)作业:《校本》第24页“基础训练”、“自我检测 ”剩下的题目.
自我检测:
1.已知函数y=(k+1)x+k2-1,当k______时,它是一次函数;当k=______时,它是正比例函数.
2.若一次函数y=kx+b的图象经过M(0,2)和N(1,3)两点,则k=________,b=________.
3.一次函数,若随的增大而增大,则的取值范围是___________.
4.下列函数中,y随x的增大而减少的函数是( )
A.y=2x+8 B.y=﹣2+4x C.y=﹣2x+8 D.y=4x
5.为庆祝商都正式营业,商都推出了两种购物方案.方案一:非会员购物所有商品价格可获九五折优惠,方案二:如交纳300元会费成为该商都会员,则所有商品价格可获九折优惠.
(1)以x(元)表示商品价格,y(元)表示支出金额,分别写出两种购物方案中y关于x的函数解析式;
(2)若某人计划在商都购买价格为5880元的电视机一台,请分析选择哪种方案更省钱?
拓展视野:
6.如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,﹣2).(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△BOC=2,求点C的坐标.
五、教学评价与反思:
本节课是初三数学总复习的第12讲一次函数的复习,我将一次函数这内容总结出五个考点,分别是:考点一:正比例函数定义、图像与性质;考点二: 一次函数的定义;考点三:一次函数的图形与性质;考点四:求一次函数解析式;考点五:一次函数与一元一次方程、一元一次不等式、二元一次方程组; 考点六:一次函数的应用.
授课过程中体现在让学生进行知识回顾、知识点小结及练习巩固等,让学生对一次函数有一个系统、直观的复习思路.在提问学生回答问题时,我不是单纯地叫学生回答,我是让学生回答完后帮老师找下一题回答的学生,这样就会使学生变被动为主动学习.例如,在“画一次函数的草图”时,回答了第一个问题的学生就找他想叫的同学回答下一个问题,使无味的复习课变得活跃了起来,增强了学习气氛.
本节课的教学方法主要有讲练结合,自主探究,同学讨论等,教学中让学生积极主动参与知识的复习过程,使学生有效地回想起一次函数的概念和应用,同时让他们获得了数学思想方法,并培养了学生探索问题的能力.
本节课在复习前面的四个考点时,学生还是很顺利的,但到了第五个考点时,我发现学生对考点五:一次函数与一元一次方程、一元一次不等式、二元一次方程组,理解有点困难,我就放慢一点节奏,但还是有部分学生反映不过来,所以,我要在接下来的练习和作业中加强这方面的训练。
总之,在本节课的教学设计时,我明确复习的主要内容,在整节课中,我不断地提问学生,让学生在老师的问题中回顾知识点,加深知识点的认识,培养学生思考和解题能力,促进学生思维发展,把沉闷的复习课“动”起来,同时,我将“自主思考、合作交流”的学习方式贯穿于课的始终,并将评价与教师的教和学生的学有机的融为一体.通过老师的提问使学生自主对知识点的回顾和思考,进一步让学生体会“函数思想”“类比思想”“数形结合思想”,为后面函数的综合题做好铺垫.我相信,在新程标准的指引下,只要我努力教学,我的数学课堂将会越来越精彩.
o
(1)当k>0时,直线y=kx,经过一、三象限,y随x的增大而增大,函数的图象从左到右上升.
o
(2)当k<0时,直线y=kx,经过二、四象限,y随x的增大而减少,函数的图象从左到右下降.
A.
o
B.
o
o
C.
D.
o
画图步骤:
1、列表;
2、描点;
3、连线。
o
(1)当k>0时,直线y=kx+b, y随x的增大而增大,函数的图象从左到右上升.
(2)当k<0时,直线y=kx+b, y随x的增大而减少,函数的图象从左到右下降.
o
o
o
(1)y=5x+3
(2)y=2x-1
(4)y=-9x-3
(3)y=-6x+2
(1)y=-x+2
(2)y=6x-1
(4)y=-5x-3
(3)y=3x+2
-4
2
o
y=-x-3
y=x-3
-3
D
C
B.
A.
(3)y=-6x+2
(4)y=-9x-3
PAGE
3
---------初三数学总复习
一、教学目标
(一)考纲要求
1、结合具体情境体会一次函数的意义,根据已知条件确定一次函数表达式.
2、会画一次函数的图象,并会利用待定系数法确定一次函数的解析式,根据一次函数的图象和解析表达式探索并理解其性质(k>0或k<0时,图象的变化情况).
3、理解正比例函数.
4、能根据一次函数的图象求二元一次方程组的近似解.
5、能用一次函数解决实际问题.
(二)过程与方法
1、通过复习进一步发展学生形象思维能力和应用数学的能力
2、发展学生数形结合意识,提高学生观察图象的能力
(三)情感态度价值观
通过复习进一步培养学生良好的学习习惯
(四)教学重难点
1、重点:一次函数的图象与性质.
2、难点:用图象法解二元一次方程组,及利用一次函数的增减性解决实际问题中的最值.
二、学情分析:
学生已经在初二学习过一次函数,现在在初三总复习中再一次复习一次函数,有的学生已经忘记了一次函数的一些知识点,所以有必要系统地给学生复习过一遍一次函数的相关内容。次节课中,学生在原有知识与学习经验对本节课的类比学习奠定扎实的学习基础,在前后知识的类比学习中,学生可以进一步理解函数的知识,体验研究函数的基本思路,促进学生的认知结构的不断的完善,进而发展学生的类比、抽象与概括能力.而这些目标的达成必须是在充分发挥学生的主体作用,给予学生足够的活动、探究、交流、反思的时间与空间,让在学生在类比中学习、在类比中思考的前提下才能完成的.
三、教学内容分析:
一次函数属于《数学课程标准》中“数与代数”领域,是最基本的、最简单的函数,一次函数在中考考察中往往跟反比例函数和二次函数结合在一起,所以复习好一次函数对之后函数的综合题有很大的帮助。
四、教学环节与活动:
(一)知识点回顾和相应题目小练
考点一:正比例函数定义、图像与性质
一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫比例系数.例如:y=5x, y=-2x都是正比例函数
正比例函数y=kx图象与性质:
对应练习:
1.下列函数中是正比例函数的是( )
A.y=-8x B.y = C.y=5x2+6 D.y = —0.5x-1
2.正比例函数y=3x的图象大致是( )
考点二: 一次函数的定义
一般地,如果y=kx+b (k、b是常数k≠0),那么y叫做x的一次函数. 例如: y=5x+3, y=-2x+9
特别地,当b=0时,一次函数y=k x+b变为正比例函数y=k x,所以正比例函数是特殊的一次函数!
对应练习:
1.下列是一次函数的有 ,是正比例函数的有 .
(1)y=-3x (2)y=6x-3 (3)y=5x+2 (4) (5) (6)y=2x
考点三:一次函数的图形与性质
1.一次函数的图像是一条直线
例如:画出一次函数y=2x+1的图象
解:列表得:
x … 0 1 …
y … 1 3 …
2.一次函数的图象与性质:
一次函数y=kx+b图象与性质:
3.例如:画出下列函数的草图:(教师示范)
4.练习:画出下列函数的草图
对应练习:
1.一次函数y=-3x-2的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.把一次函数y=-3x+6向下平移5个单位长度得到的直线解析式是 .
3. 若直线y=-4x+5与y=kx+1平行,则k= .
考点四:求一次函数解析式
求一次函数解析式的方法是:待定系数法
1.已知正比例函数图象经过点(2,8),则这个正比例函数的解析式是: .
2.已知一次函数的图象经过点(3,5)与(-4,-9),求这个一次函数的解析式.
考点五:一次函数与一元一次方程、一元一次不等式、二元一次方程组.
1.直线y=2x+6与x轴的交点坐标是 ,与y轴的交点坐标是 .
2.观察函数y=2x-4的图象,回答下列问题:
(1)当x , 2x-4>0?
(2)当x , 2x-4<0
3.一次函数y=-x-3与y=x-3的图象如图所示,则这两个函
数图象的交点坐标是 ,方程组 的解是
考点六:一次函数的应用
1.某市出租车计费方法如图所示,请根据图象回答
下面的问题:
(1)出租车的起步价是 元,在路程 千米内只收起步价.
(2)表示路程s大于3km时,费用y与s之间的函数关系式
是 .
(3)某乘客坐出租车,车费为31元,则他乘车的路程是 千米.
(二)课堂练习:《校本》第24页“基础训练”
基础训练:
1.已知函数y=4x+5,当x=-3时,y=___;当y=5时,x=___.
2. 函数y=xm-8是正比例函数,则m=______,y随x的增大而________.
3.一次函数y=2x-3的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第一象限
4.已知直线y=kx+b中,当x1>x2时,y1>y2,则下列结论中一定正确的是( )
A.k>0 B.k<0 C.b>0 D.b<0
5.将直线y=2x向下平移1个单位后所得图象对应的函数解析式为( )
A.y=2x-1 B.y=2x-2
C.y=2x+1 D.y=2x+2
6.若实数a,b满足ab<0,且a<b,则函数y=ax+b的图象可能是( )
7.如图,一次函数y=﹣x+m的图象和y轴交于点B,与正比例函数y=x图象交于点P (2,n).
(1)求m和n的值;
(2)求△POB的面积.
(三)小结:(引导学生回顾复习的知识点)
1、正比例函数定义、图像与性质
2、一次函数的定义
3、一次函数的图形与性质
4、求一次函数解析式
5、一次函数与一元一次方程、一元一次不等式、二元一次方程组
6、一次函数的应用
(四)作业:《校本》第24页“基础训练”、“自我检测 ”剩下的题目.
自我检测:
1.已知函数y=(k+1)x+k2-1,当k______时,它是一次函数;当k=______时,它是正比例函数.
2.若一次函数y=kx+b的图象经过M(0,2)和N(1,3)两点,则k=________,b=________.
3.一次函数,若随的增大而增大,则的取值范围是___________.
4.下列函数中,y随x的增大而减少的函数是( )
A.y=2x+8 B.y=﹣2+4x C.y=﹣2x+8 D.y=4x
5.为庆祝商都正式营业,商都推出了两种购物方案.方案一:非会员购物所有商品价格可获九五折优惠,方案二:如交纳300元会费成为该商都会员,则所有商品价格可获九折优惠.
(1)以x(元)表示商品价格,y(元)表示支出金额,分别写出两种购物方案中y关于x的函数解析式;
(2)若某人计划在商都购买价格为5880元的电视机一台,请分析选择哪种方案更省钱?
拓展视野:
6.如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,﹣2).(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△BOC=2,求点C的坐标.
五、教学评价与反思:
本节课是初三数学总复习的第12讲一次函数的复习,我将一次函数这内容总结出五个考点,分别是:考点一:正比例函数定义、图像与性质;考点二: 一次函数的定义;考点三:一次函数的图形与性质;考点四:求一次函数解析式;考点五:一次函数与一元一次方程、一元一次不等式、二元一次方程组; 考点六:一次函数的应用.
授课过程中体现在让学生进行知识回顾、知识点小结及练习巩固等,让学生对一次函数有一个系统、直观的复习思路.在提问学生回答问题时,我不是单纯地叫学生回答,我是让学生回答完后帮老师找下一题回答的学生,这样就会使学生变被动为主动学习.例如,在“画一次函数的草图”时,回答了第一个问题的学生就找他想叫的同学回答下一个问题,使无味的复习课变得活跃了起来,增强了学习气氛.
本节课的教学方法主要有讲练结合,自主探究,同学讨论等,教学中让学生积极主动参与知识的复习过程,使学生有效地回想起一次函数的概念和应用,同时让他们获得了数学思想方法,并培养了学生探索问题的能力.
本节课在复习前面的四个考点时,学生还是很顺利的,但到了第五个考点时,我发现学生对考点五:一次函数与一元一次方程、一元一次不等式、二元一次方程组,理解有点困难,我就放慢一点节奏,但还是有部分学生反映不过来,所以,我要在接下来的练习和作业中加强这方面的训练。
总之,在本节课的教学设计时,我明确复习的主要内容,在整节课中,我不断地提问学生,让学生在老师的问题中回顾知识点,加深知识点的认识,培养学生思考和解题能力,促进学生思维发展,把沉闷的复习课“动”起来,同时,我将“自主思考、合作交流”的学习方式贯穿于课的始终,并将评价与教师的教和学生的学有机的融为一体.通过老师的提问使学生自主对知识点的回顾和思考,进一步让学生体会“函数思想”“类比思想”“数形结合思想”,为后面函数的综合题做好铺垫.我相信,在新程标准的指引下,只要我努力教学,我的数学课堂将会越来越精彩.
o
(1)当k>0时,直线y=kx,经过一、三象限,y随x的增大而增大,函数的图象从左到右上升.
o
(2)当k<0时,直线y=kx,经过二、四象限,y随x的增大而减少,函数的图象从左到右下降.
A.
o
B.
o
o
C.
D.
o
画图步骤:
1、列表;
2、描点;
3、连线。
o
(1)当k>0时,直线y=kx+b, y随x的增大而增大,函数的图象从左到右上升.
(2)当k<0时,直线y=kx+b, y随x的增大而减少,函数的图象从左到右下降.
o
o
o
(1)y=5x+3
(2)y=2x-1
(4)y=-9x-3
(3)y=-6x+2
(1)y=-x+2
(2)y=6x-1
(4)y=-5x-3
(3)y=3x+2
-4
2
o
y=-x-3
y=x-3
-3
D
C
B.
A.
(3)y=-6x+2
(4)y=-9x-3
PAGE
3
同课章节目录
