2.4用因式分解法求解一元二次方程 课件(共14张PPT)
文档属性
| 名称 | 2.4用因式分解法求解一元二次方程 课件(共14张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-11 12:40:45 | ||
图片预览






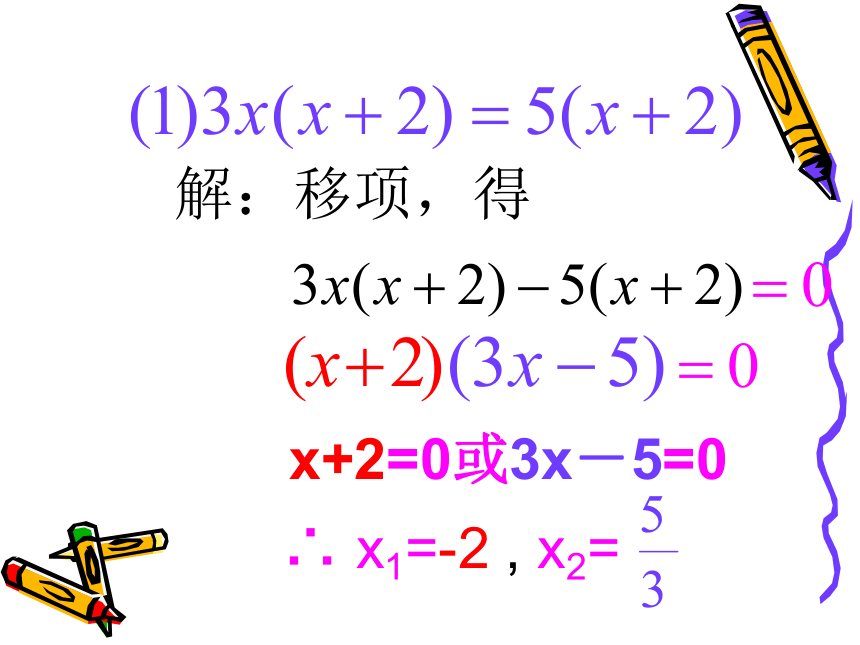
文档简介
(共14张PPT)
用直接开平方法可解下列类型的一元二次方程:
根据平方根的定义,要特别注意:由于负数没有平方根,
所以当b<0时,原方程无解。
知识回顾
大胆猜测:使下列式子成立的x为多少?
AB=0 A=0或B=0
知识回顾
解:
(直接开平方法):
例2:解方程x2- 4=0.
另解:原方程可变形为
(x+2)(x-2)=0
x+2=0 或 x-2=0
∴ x1=-2 ,x2=2
我们观察可以发现
可以使用平方差公式
以上解某些一元二次方程的方法叫做因式分解法。
x2-4=(x-2)(x+2)
例3 解下列方程:
x+2=0或3x-5=0
∴ x1=-2 , x2=
解:原方程可变形为
归纳:用因式分解法解一元二次方程的步骤
1 . 方程右边不为零的化为 。
2 . 将方程左边分解成两个 的乘积。
3 . 至少 一次因式为零,得到两个一元一次方程。
4 . 两个 就是原方程的解。
零
一次因式
有一个
一元一次方程的解
例 (x+3)(x-1)=5
解:原方程可变形为
(x-2)(x+4)=0
x-2=0或x+4=0
∴ x1=2 ,x2=-4
解题步骤演示
方程右边化为零
x2+2x-8 =0
左边分解成两个一次因式 的乘积
至少有一个一次因式为零得到两个一元一次方程
两个一元一次方程的解就是原方程的解
这样解是否正确呢?
方程的两边同时除以同一个不等于零的数,所得的方程与原方程 同解。
拓展练习1:辨析
2、下面的解法正确吗?如果不正确,错误在哪?
( )
用因式分解法解一元二次方程的步骤
1. 方程右边不为零的化为 。
2 .将方程左边分解成两个 的乘积。
3 .至少 一次因式为零,得到两个一元一次方程。
4 .两个 就是原方程的解。
零
一次因式
有一个
一元一次方程的解
小结
再 见 碑
用直接开平方法可解下列类型的一元二次方程:
根据平方根的定义,要特别注意:由于负数没有平方根,
所以当b<0时,原方程无解。
知识回顾
大胆猜测:使下列式子成立的x为多少?
AB=0 A=0或B=0
知识回顾
解:
(直接开平方法):
例2:解方程x2- 4=0.
另解:原方程可变形为
(x+2)(x-2)=0
x+2=0 或 x-2=0
∴ x1=-2 ,x2=2
我们观察可以发现
可以使用平方差公式
以上解某些一元二次方程的方法叫做因式分解法。
x2-4=(x-2)(x+2)
例3 解下列方程:
x+2=0或3x-5=0
∴ x1=-2 , x2=
解:原方程可变形为
归纳:用因式分解法解一元二次方程的步骤
1 . 方程右边不为零的化为 。
2 . 将方程左边分解成两个 的乘积。
3 . 至少 一次因式为零,得到两个一元一次方程。
4 . 两个 就是原方程的解。
零
一次因式
有一个
一元一次方程的解
例 (x+3)(x-1)=5
解:原方程可变形为
(x-2)(x+4)=0
x-2=0或x+4=0
∴ x1=2 ,x2=-4
解题步骤演示
方程右边化为零
x2+2x-8 =0
左边分解成两个一次因式 的乘积
至少有一个一次因式为零得到两个一元一次方程
两个一元一次方程的解就是原方程的解
这样解是否正确呢?
方程的两边同时除以同一个不等于零的数,所得的方程与原方程 同解。
拓展练习1:辨析
2、下面的解法正确吗?如果不正确,错误在哪?
( )
用因式分解法解一元二次方程的步骤
1. 方程右边不为零的化为 。
2 .将方程左边分解成两个 的乘积。
3 .至少 一次因式为零,得到两个一元一次方程。
4 .两个 就是原方程的解。
零
一次因式
有一个
一元一次方程的解
小结
再 见 碑
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
