2.7 有理数的乘法(2) 课件(共15张PPT)
文档属性
| 名称 | 2.7 有理数的乘法(2) 课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 806.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
北师大版七年级上册
2.7有理数的乘法
(第二课时)
有理数乘法法则
两数相乘,同号得正,异号得负,并把绝对值相乘。任何数同0相乘,都得0。
=1 ;
=1 ;
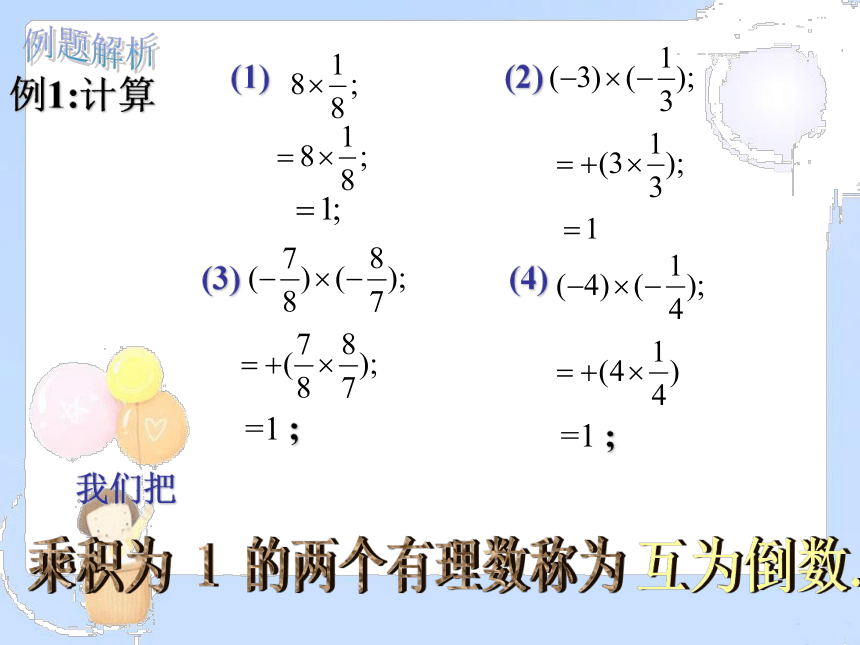
例1:计算
(3) (4)
(1) (2)
我们把
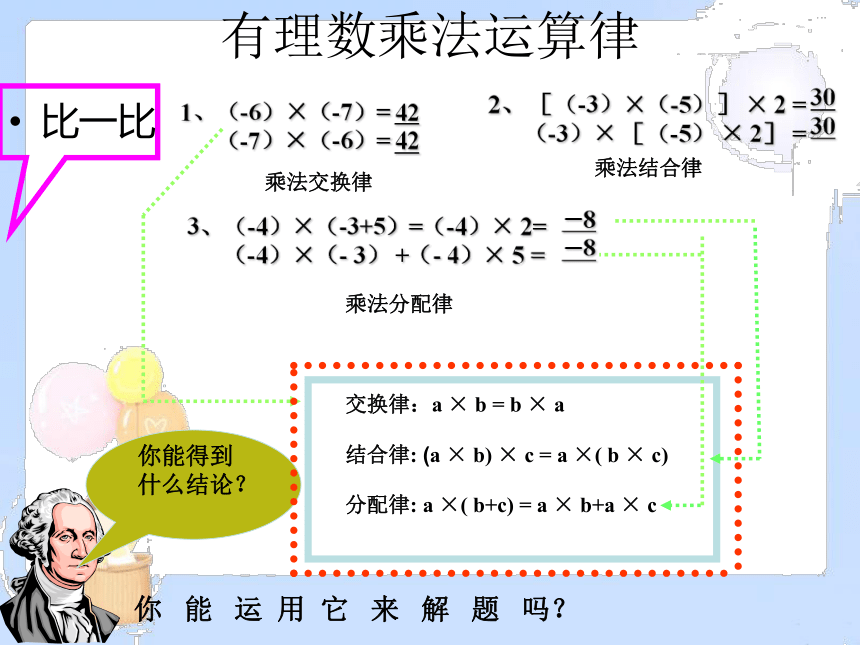
有理数乘法运算律
比一比
1、(-6)×(-7)=
(-7)×(-6)=
2、 [(-3)×(-5)] × 2 =
(-3)× [(-5) × 2] =
3、(-4)×(-3+5)=(-4)× 2=
(-4)×(- 3) +(- 4)× 5 =
乘法交换律
乘法结合律
乘法分配律
42
你能得到什么结论?
42
30
30
-8
-8
交换律:a × b = b × a
结合律: (a × b) × c = a ×( b × c)
分配律: a ×( b+c) = a × b+a × c
你 能 运 用 它 来 解 题 吗?
例2
计算
[
]
应运了哪一
个定律呀?
你理解
了吗?
变式 :
计算:
分析:细心观察本题三项积中,都有 这个因数,所以可逆用乘法分配律求解.
解:原式
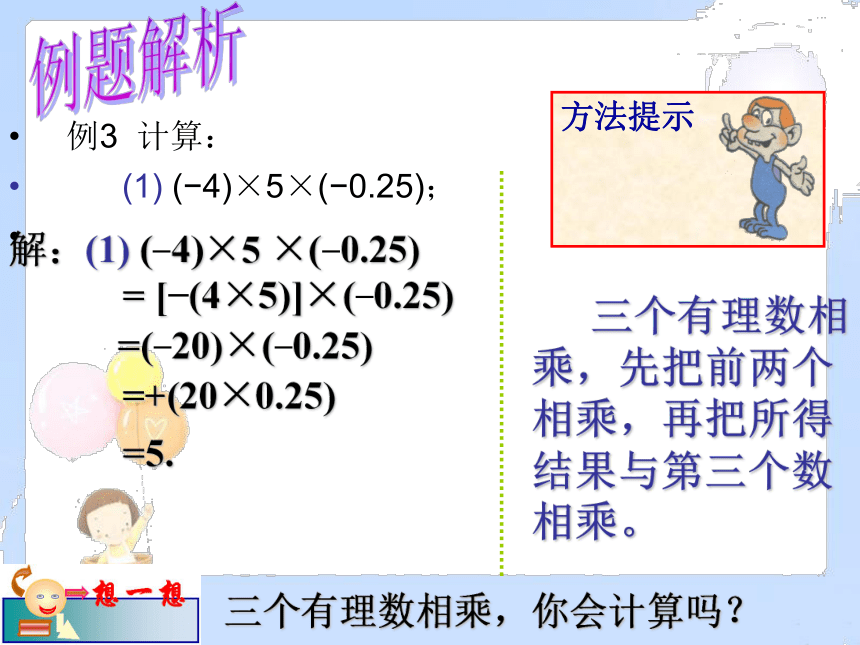
例3 计算:
(1) ( 4)×5×( 0.25);
解:(1) ( 4)×5 ×( 0.25)
= [ (4×5)]×( 0.25)
=+(20×0.25)
=5.
=( 20)×( 0.25)
方法提示
三个有理数相乘,先把前两个相乘,再把所得结果与第三个数相乘。
三个有理数相乘,你会计算吗?
例4 计算:
解:
对于本例的求解,是连续两次使用乘法法则。
= 1 .
解题后的反思
如果我们把乘法法则推广到三个有理数相乘,只“一次性地”先定号再绝对值相乘,
那么各小题中的“ 积”应分别是什么符号?
观察下列各式,它们的积是正的还是负的?
(1)(-1) ×2 ×3 ×4 ;
(2)(-1) ×(-2 )×3 ×4;
(3) (-1) ×(-2 )×(-3 )×4;
(4) (-1) ×(-2 )×(-3 )×(-4)
(5) (-1) ×(-2 )×(-3 )×(-4)×0
乘积的符号的确定
以例3、例4为例 :
(1) ( 4)×5×( 0.25) (2)
解:(1) ( 4)×5 ×( 0.25) (2)
= (4×5×0.25)
几个有理数相乘,因数都不为 0 时,
积的符号怎样确定?
+
有一因数为 0 时,积是多少?
乘积 的符号 的确定
几个有理数相乘,因数都不为 0 时,
积的符号由 确定:
负因数的个数
奇数个为负,偶数个为正。
有一因数为 0 时,积是
0 .
(1)3×(-5)=(-5)×(-3)
(2)-7.25×7.26+7.25×(-7.29)
=(-7.25)×[7.26+(-7.29)]
(3)(-6)×[(-0.5)-1.3]
=(-6)×(-0.5)+(-6)×1.3
(4)[(-10)×1.3]×0.3
=(-10)×[0.3 +1.3]
(5)(-8)×(-9)= 9×8
找 错
这题有错吗?错在哪里?
某校体育器材室共有60个篮球,一天课外活动,有3个班级分别计划借篮球总数的 , 和 。请你算一算,这60个篮球够借吗?如果够了,还多几个篮球?如果不够,还缺几个?
再 见
北师大版七年级上册
2.7有理数的乘法
(第二课时)
有理数乘法法则
两数相乘,同号得正,异号得负,并把绝对值相乘。任何数同0相乘,都得0。
=1 ;
=1 ;
例1:计算
(3) (4)
(1) (2)
我们把
有理数乘法运算律
比一比
1、(-6)×(-7)=
(-7)×(-6)=
2、 [(-3)×(-5)] × 2 =
(-3)× [(-5) × 2] =
3、(-4)×(-3+5)=(-4)× 2=
(-4)×(- 3) +(- 4)× 5 =
乘法交换律
乘法结合律
乘法分配律
42
你能得到什么结论?
42
30
30
-8
-8
交换律:a × b = b × a
结合律: (a × b) × c = a ×( b × c)
分配律: a ×( b+c) = a × b+a × c
你 能 运 用 它 来 解 题 吗?
例2
计算
[
]
应运了哪一
个定律呀?
你理解
了吗?
变式 :
计算:
分析:细心观察本题三项积中,都有 这个因数,所以可逆用乘法分配律求解.
解:原式
例3 计算:
(1) ( 4)×5×( 0.25);
解:(1) ( 4)×5 ×( 0.25)
= [ (4×5)]×( 0.25)
=+(20×0.25)
=5.
=( 20)×( 0.25)
方法提示
三个有理数相乘,先把前两个相乘,再把所得结果与第三个数相乘。
三个有理数相乘,你会计算吗?
例4 计算:
解:
对于本例的求解,是连续两次使用乘法法则。
= 1 .
解题后的反思
如果我们把乘法法则推广到三个有理数相乘,只“一次性地”先定号再绝对值相乘,
那么各小题中的“ 积”应分别是什么符号?
观察下列各式,它们的积是正的还是负的?
(1)(-1) ×2 ×3 ×4 ;
(2)(-1) ×(-2 )×3 ×4;
(3) (-1) ×(-2 )×(-3 )×4;
(4) (-1) ×(-2 )×(-3 )×(-4)
(5) (-1) ×(-2 )×(-3 )×(-4)×0
乘积的符号的确定
以例3、例4为例 :
(1) ( 4)×5×( 0.25) (2)
解:(1) ( 4)×5 ×( 0.25) (2)
= (4×5×0.25)
几个有理数相乘,因数都不为 0 时,
积的符号怎样确定?
+
有一因数为 0 时,积是多少?
乘积 的符号 的确定
几个有理数相乘,因数都不为 0 时,
积的符号由 确定:
负因数的个数
奇数个为负,偶数个为正。
有一因数为 0 时,积是
0 .
(1)3×(-5)=(-5)×(-3)
(2)-7.25×7.26+7.25×(-7.29)
=(-7.25)×[7.26+(-7.29)]
(3)(-6)×[(-0.5)-1.3]
=(-6)×(-0.5)+(-6)×1.3
(4)[(-10)×1.3]×0.3
=(-10)×[0.3 +1.3]
(5)(-8)×(-9)= 9×8
找 错
这题有错吗?错在哪里?
某校体育器材室共有60个篮球,一天课外活动,有3个班级分别计划借篮球总数的 , 和 。请你算一算,这60个篮球够借吗?如果够了,还多几个篮球?如果不够,还缺几个?
再 见
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
