3.3 探索三角形全等的条件(3) 课件(共18张PPT)
文档属性
| 名称 | 3.3 探索三角形全等的条件(3) 课件(共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 583.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-11 11:47:07 | ||
图片预览




文档简介
(共18张PPT)
北师大版七年级 下册
(第3课时)
1.判断三角形全等至少要有几个条件?
至少要有三个条件.
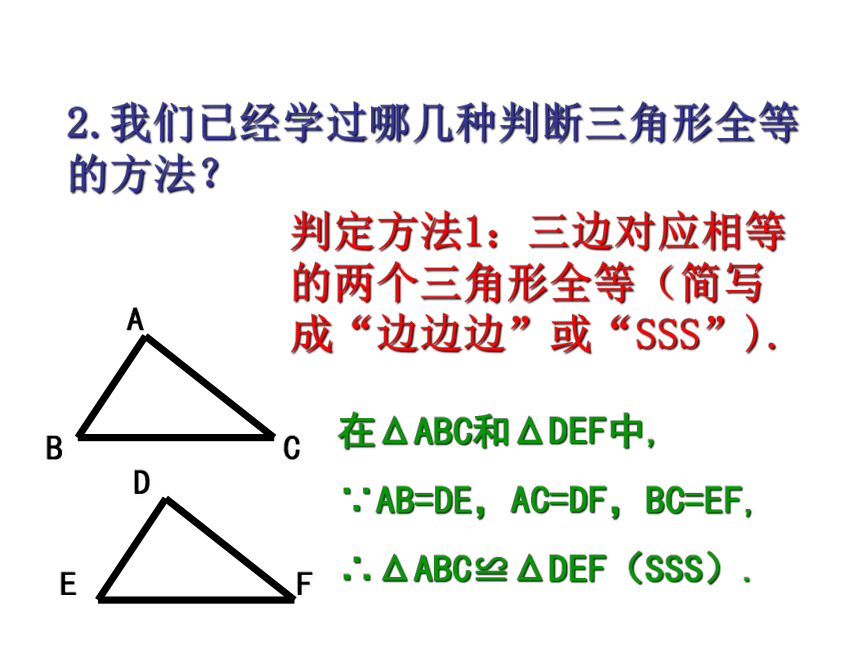
2.我们已经学过哪几种判断三角形全等的方法?
A
B
C
D
E
F
在ΔABC和ΔDEF中,
∵AB=DE,AC=DF,BC=EF,
∴ΔABC≌ΔDEF(SSS).
判定方法1:三边对应相等的两个三角形全等(简写成“边边边”或“SSS”).
A
B
C
D
E
F
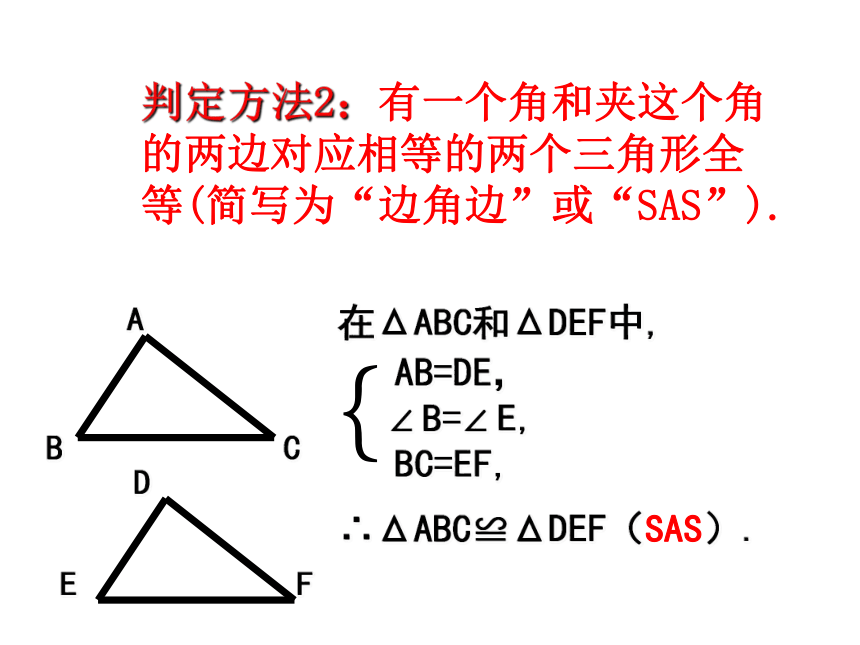
判定方法2:有一个角和夹这个角的两边对应相等的两个三角形全等(简写为“边角边”或“SAS”).
{
在ΔABC和ΔDEF中,
AB=DE,
∠ B=∠ E,
BC=EF,
∴ΔABC≌ΔDEF(SAS).
如图,小明不慎将一块三角形模具打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具呢 如果可以,带哪块去合适 你能说明其中理由吗
问题1:如果已知一个三角形的两角及一边,那么有几种可能的情况呢?
角边角 角角边
A
B
C
600
450
3cm
E
G
F
600
450
3cm
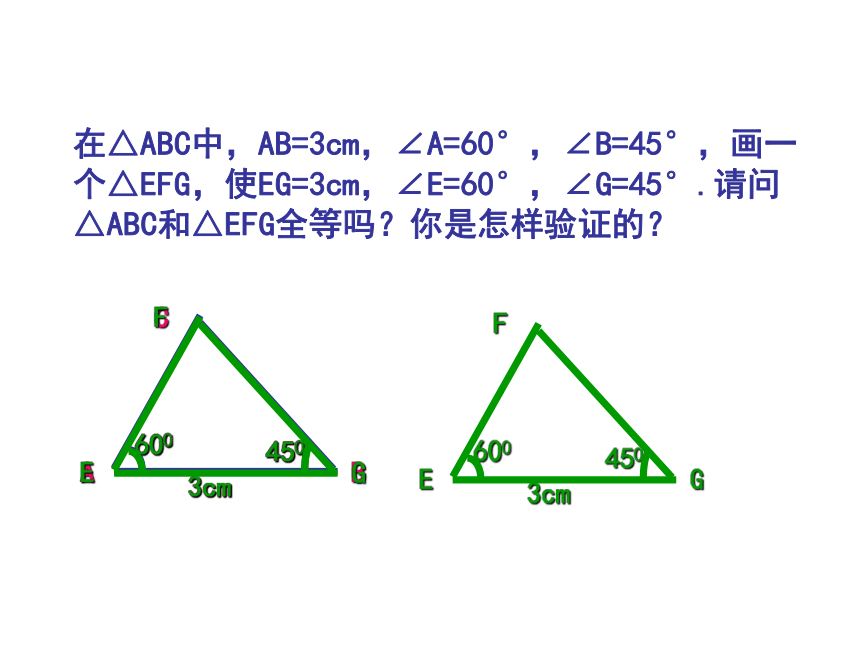
在△ABC中,AB=3cm,∠A=60°,∠B=45°,画一个△EFG,使EG=3cm,∠E=60°,∠G=45°.请问△ABC和△EFG全等吗?你是怎样验证的?
E
G
F
600
450
3cm
有两个角和这两个角的夹边对应相等的两个三角形全等(简写成“角边角”或“ASA”).
判定方法3
在ΔABC和Δ DEF中,
∠A= ∠D,
AC=DF,
∠C=∠F,
解 ∵ ∠A+∠B+∠C=180°,
∠D+∠E+∠F=180°,
(三角形的内角和等于180°)
A
B
C
D
E
F
在ΔABC和ΔDEF中,∠B=∠E,∠C=∠F,AC=DF,请说明ΔABC≌ΔDEF.
∴ ∠A=180°-∠B-∠C,
∠D=180°-∠E-∠F.
∵ ∠B=∠E ,∠C=∠F,
∴ ∠A= ∠D.
∴ΔABC≌ΔDEF(ASA).
有两个角和其中一个角的对边对应相等的两个三角形全等(简写成“角角边”或“AAS”).
判定方法4
三角形全等的判定方法3:∵∠B=∠E,BC=EF,∠C=∠F,
∴ΔABC≌DEF(ASA).
三角形全等的判定方法4:∵ ∠B=∠E ,∠C=∠F,AC=DF,
∴ΔABC≌DEF(AAS).
A
B
C
D
E
F
A
B
C
D
E
F
如图,小明不慎将一块三角形模具打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗 如果可以,带哪块去合适 你能说明其中理由吗
有两个角和这两个角的夹边对应相等的两个三角形全等.
( )
公共边
练一练
完成下列推理过程:
在△ABC和△DCB中,
∠ABC=∠DCB
∵ BC=CB
∴△ABC≌△DCB( )
ASA
A
B
C
D
O
1
2
3
4
∠2=∠1
AAS
∠3=∠4
∠2=∠1
CB=BC
例5 如图,点P是∠BAC的平分线上的一点,PB⊥AB,PC⊥AC.说明PB=PC的理由.
解 ∵ PB⊥AB,PC⊥AC,
A
B
C
P
∴ ∠ABP=∠ACP(垂线的意义),
在ΔABP和ΔACP中,
∠PAB=∠PAC (角平分线的意义),
∠ABP=∠ACP,
AP=AP(公共边),
∴ ΔABP≌ΔACP(AAS).
∴ PB=PC(全等三角形的对应边相等).
角平分线上的点到角两边的距离相等.
应 用:
∵P 是∠BAC的平分线上的点,
PB⊥AB,PC⊥AC,∴PB=PC(角平分线上的点到角
两边的距离相等).
A
B
C
P
D
C
B
A
1、在△ABC中,AB=AC,AD是边BC上的中线.请说明∠BAD=∠CAD的理由.
解 ∵AD是BC边上的中线, ∴BD=CD(三角形中线的定义), 在△ABD和△ACD中,
∴ △ABD≌△ACD(SSS),
∴ ∠BAD=∠CAB(全等三角形对应角相等).
AD是∠BAC的角平分线.
请说明BD=CD的理由.
解 ∵AD是∠BAC的角平分线(已知),
∴∠BAD=∠CAD(角平分线的定义),
∵AB=AC(已知),∠BAD=∠CAD(已证),
AD=AD(公共边),
∴△ABD≌△ACD(SAS),
∴BD=CD(全等三角形对应边相等).
(1) 两角和它们的夹边对应相等的两个三角形全等.
简写成“角边角”或“ASA”.
(2) 两角和其中一角的对边对应相等的两个三角形全等.
简写成“角角边”或“AAS”.
知识要点:
(3)探索三角形全等是证明线段相等(对应边相等),
角相等(对应角相等)等问题的基本途径.
数学思想:
要学会用分类的思想,转化的思想解决问题。
再 见
北师大版七年级 下册
(第3课时)
1.判断三角形全等至少要有几个条件?
至少要有三个条件.
2.我们已经学过哪几种判断三角形全等的方法?
A
B
C
D
E
F
在ΔABC和ΔDEF中,
∵AB=DE,AC=DF,BC=EF,
∴ΔABC≌ΔDEF(SSS).
判定方法1:三边对应相等的两个三角形全等(简写成“边边边”或“SSS”).
A
B
C
D
E
F
判定方法2:有一个角和夹这个角的两边对应相等的两个三角形全等(简写为“边角边”或“SAS”).
{
在ΔABC和ΔDEF中,
AB=DE,
∠ B=∠ E,
BC=EF,
∴ΔABC≌ΔDEF(SAS).
如图,小明不慎将一块三角形模具打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具呢 如果可以,带哪块去合适 你能说明其中理由吗
问题1:如果已知一个三角形的两角及一边,那么有几种可能的情况呢?
角边角 角角边
A
B
C
600
450
3cm
E
G
F
600
450
3cm
在△ABC中,AB=3cm,∠A=60°,∠B=45°,画一个△EFG,使EG=3cm,∠E=60°,∠G=45°.请问△ABC和△EFG全等吗?你是怎样验证的?
E
G
F
600
450
3cm
有两个角和这两个角的夹边对应相等的两个三角形全等(简写成“角边角”或“ASA”).
判定方法3
在ΔABC和Δ DEF中,
∠A= ∠D,
AC=DF,
∠C=∠F,
解 ∵ ∠A+∠B+∠C=180°,
∠D+∠E+∠F=180°,
(三角形的内角和等于180°)
A
B
C
D
E
F
在ΔABC和ΔDEF中,∠B=∠E,∠C=∠F,AC=DF,请说明ΔABC≌ΔDEF.
∴ ∠A=180°-∠B-∠C,
∠D=180°-∠E-∠F.
∵ ∠B=∠E ,∠C=∠F,
∴ ∠A= ∠D.
∴ΔABC≌ΔDEF(ASA).
有两个角和其中一个角的对边对应相等的两个三角形全等(简写成“角角边”或“AAS”).
判定方法4
三角形全等的判定方法3:∵∠B=∠E,BC=EF,∠C=∠F,
∴ΔABC≌DEF(ASA).
三角形全等的判定方法4:∵ ∠B=∠E ,∠C=∠F,AC=DF,
∴ΔABC≌DEF(AAS).
A
B
C
D
E
F
A
B
C
D
E
F
如图,小明不慎将一块三角形模具打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗 如果可以,带哪块去合适 你能说明其中理由吗
有两个角和这两个角的夹边对应相等的两个三角形全等.
( )
公共边
练一练
完成下列推理过程:
在△ABC和△DCB中,
∠ABC=∠DCB
∵ BC=CB
∴△ABC≌△DCB( )
ASA
A
B
C
D
O
1
2
3
4
∠2=∠1
AAS
∠3=∠4
∠2=∠1
CB=BC
例5 如图,点P是∠BAC的平分线上的一点,PB⊥AB,PC⊥AC.说明PB=PC的理由.
解 ∵ PB⊥AB,PC⊥AC,
A
B
C
P
∴ ∠ABP=∠ACP(垂线的意义),
在ΔABP和ΔACP中,
∠PAB=∠PAC (角平分线的意义),
∠ABP=∠ACP,
AP=AP(公共边),
∴ ΔABP≌ΔACP(AAS).
∴ PB=PC(全等三角形的对应边相等).
角平分线上的点到角两边的距离相等.
应 用:
∵P 是∠BAC的平分线上的点,
PB⊥AB,PC⊥AC,∴PB=PC(角平分线上的点到角
两边的距离相等).
A
B
C
P
D
C
B
A
1、在△ABC中,AB=AC,AD是边BC上的中线.请说明∠BAD=∠CAD的理由.
解 ∵AD是BC边上的中线, ∴BD=CD(三角形中线的定义), 在△ABD和△ACD中,
∴ △ABD≌△ACD(SSS),
∴ ∠BAD=∠CAB(全等三角形对应角相等).
AD是∠BAC的角平分线.
请说明BD=CD的理由.
解 ∵AD是∠BAC的角平分线(已知),
∴∠BAD=∠CAD(角平分线的定义),
∵AB=AC(已知),∠BAD=∠CAD(已证),
AD=AD(公共边),
∴△ABD≌△ACD(SAS),
∴BD=CD(全等三角形对应边相等).
(1) 两角和它们的夹边对应相等的两个三角形全等.
简写成“角边角”或“ASA”.
(2) 两角和其中一角的对边对应相等的两个三角形全等.
简写成“角角边”或“AAS”.
知识要点:
(3)探索三角形全等是证明线段相等(对应边相等),
角相等(对应角相等)等问题的基本途径.
数学思想:
要学会用分类的思想,转化的思想解决问题。
再 见
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
