14.2.三角形全等的判定(第1课时) 课件(共14张PPT)
文档属性
| 名称 | 14.2.三角形全等的判定(第1课时) 课件(共14张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-09 00:00:00 | ||
图片预览


文档简介
(共14张PPT)
B
A'
B'
C'
A
C
活 动 一
第一组:一条边为6cm;
第二组:一个角是45°;
第三组:两条边分别为4cm和6cm;
第四组:一条边为6cm,一个角为45°;
第五组:两个角分别为45°和60°.
按下列条件做三角形,并通过比较判断它们之间是否全等,由此你有什么发现
大家要合作哦
活 动 二
利用你手中的材料做一个三角形,使∠A的两边分别为6cm和10cm,同位进行比较并判断它们之间的关系,由此你有什么结论吗
A
结论:两边和它们的夹角对应相等的三角形全等.简记为“边角边”或“SAS”。
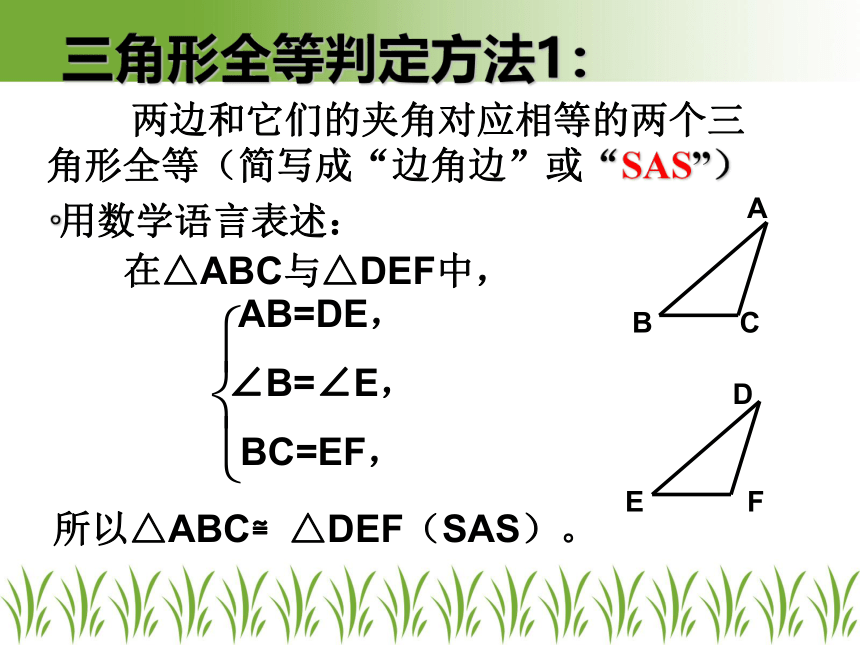
三角形全等判定方法1:
用数学语言表述:
在△ABC与△DEF中,
AB=DE,
∠B=∠E,
BC=EF,
所以△ABC≌△DEF(SAS)。
A
B
C
D
E
F
两边和它们的夹角对应相等的两个三角形全等(简写成“边角边”或“SAS”)。
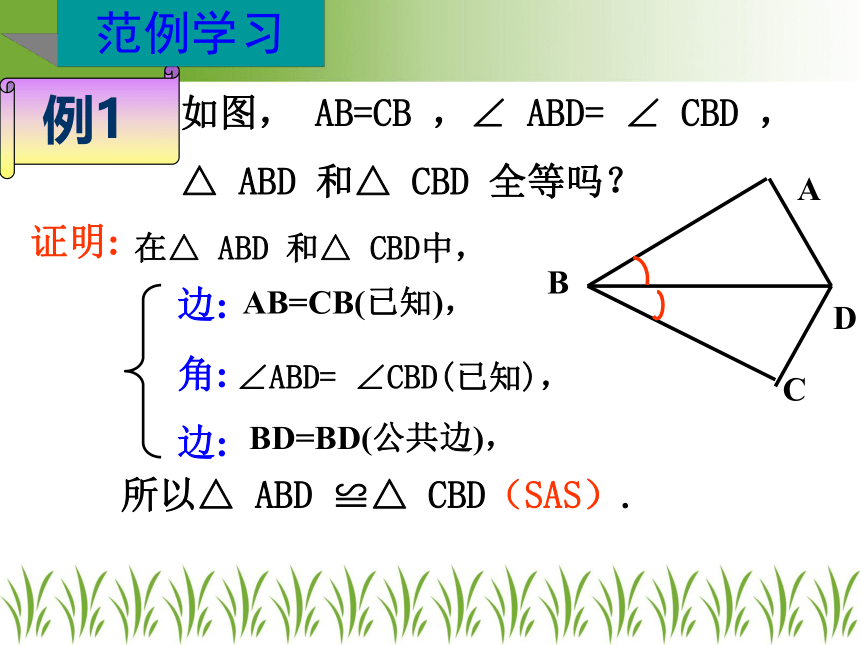
如图, AB=CB ,∠ ABD= ∠ CBD ,
△ ABD 和△ CBD 全等吗?
例1
证明:
所以△ ABD ≌△ CBD(SAS).
边:
角:
边:
AB=CB(已知),
∠ABD= ∠CBD(已知),
BD=BD(公共边),
A
B
C
D
在△ ABD 和△ CBD中,
范例学习
活 动 三
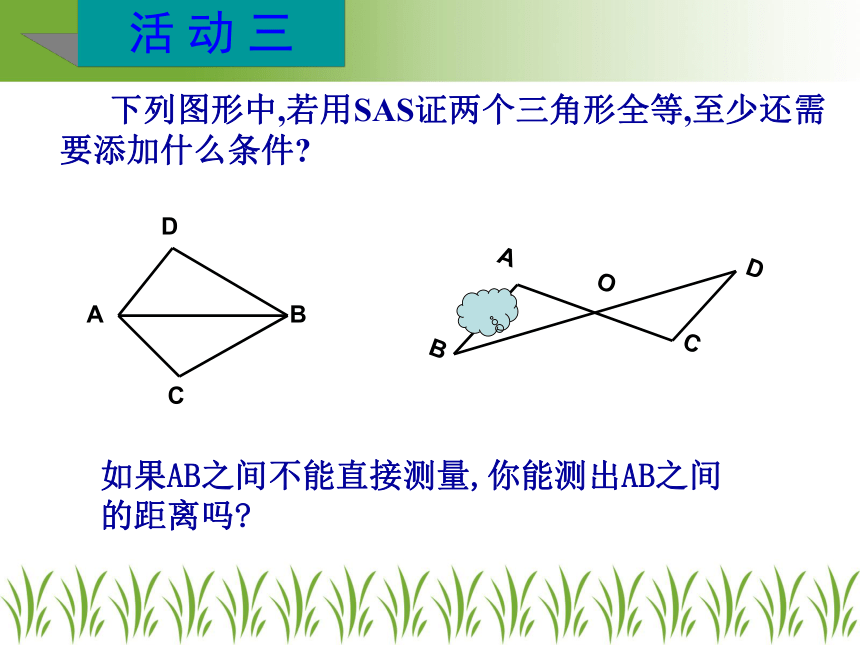
下列图形中,若用SAS证两个三角形全等,至少还需要添加什么条件
如果AB之间不能直接测量,你能测出AB之间的距离吗
A
B
C
D
O
D
C
A
B
范例学习
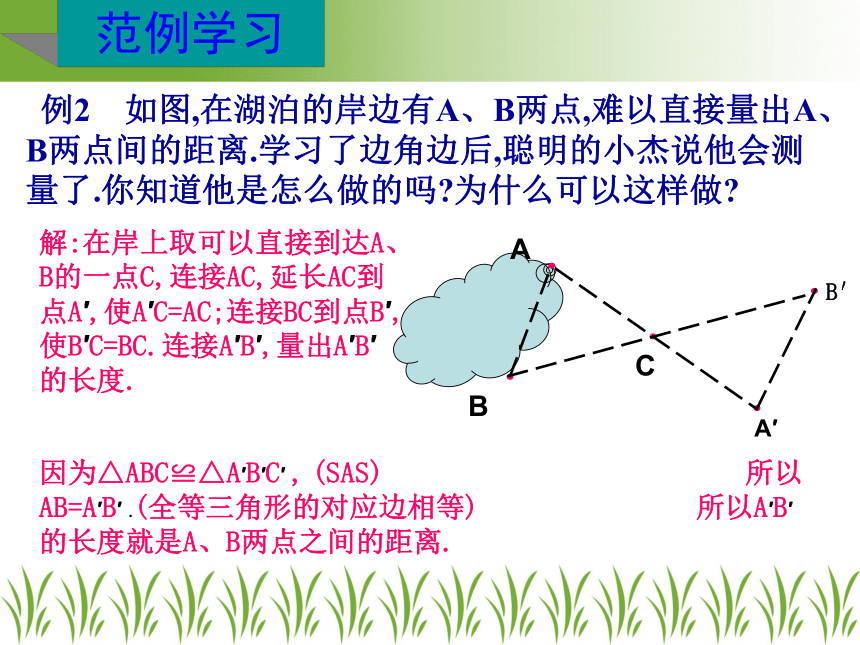
例2 如图,在湖泊的岸边有A、B两点,难以直接量出A、B两点间的距离.学习了边角边后,聪明的小杰说他会测量了.你知道他是怎么做的吗 为什么可以这样做
A
B
C
A′
B′
因为△ABC≌△A′B′C′ , (SAS) 所以AB=A′B′ .(全等三角形的对应边相等) 所以A′B′的长度就是A、B两点之间的距离.
解:在岸上取可以直接到达A、B的一点C,连接AC,延长AC到点A′,使A′C=AC;连接BC到点B′,使B′C=BC.连接A′B′,量出A′B′的长度.
范例学习
例3 已知:如图,AD∥BC,AD=BC,
求证:△ADC≌△CBA.
证明:∵AD∥BC(已知)
∴∠DAC=∠BCA.(两直线平行,内错角相等)
在△ADC和△CBA中,
AD=BC,(已知)
∠DAC=∠BCA,(已证)
AC=CA,(公共边)
∴△ADC≌△CBA.(SAS)
A
B
C
D
准备条件
指出范围
列举条件
得出结论
牛刀小试
已知:如图,AB=DB,CB=EB,∠1=∠2.
求证:∠A=∠D.
证明:∵∠1=∠2,(已知)
∴∠1+∠DBC=∠2+∠DBC.(等式的性质)
即∠ABC=∠DBE.
在△ABC和△DBE中,
AB=DB,(已知)
∠ABC=∠DBE,(已证)
CB=EB,(已知)
∴△ABC≌△DBE.(SAS)
∴∠A=∠D.(全等三角形的对应角相等)
1
A
2
C
B
D
E
以2.5cm,3.5cm为三角形的两边,长度为2.5cm的边所对的角为40° ,情况又怎样?动手画一画,你发现了什么?
A
B
C
D
E
F
2.5cm
3.5cm
40°
40°
3.5cm
2.5cm
结论:两边及其一边所对的角相等,两个三角形不一定全等
探究
猜一猜:
是不是二条边和一个角对应相等,这样的两个三角形一定全等吗?你能举例说明吗?
如图△ABC与△ABD中,AB=AB,AC=BD, ∠B=∠B
他们全等吗?
B
A
C
D
注:这个角一定要是这两边所夹的角
小 结
1.学习了本节课以后,你有哪些收获
2.你还有什么疑惑
思 考
学习本节课后,我们知道已知两边及其夹角这三对元素对应相等,就可以判断两三角形全等,那么两个三角形具备其他三组元素对应相等,他们是否也能得到两个三角形全等
再 见
B
A'
B'
C'
A
C
活 动 一
第一组:一条边为6cm;
第二组:一个角是45°;
第三组:两条边分别为4cm和6cm;
第四组:一条边为6cm,一个角为45°;
第五组:两个角分别为45°和60°.
按下列条件做三角形,并通过比较判断它们之间是否全等,由此你有什么发现
大家要合作哦
活 动 二
利用你手中的材料做一个三角形,使∠A的两边分别为6cm和10cm,同位进行比较并判断它们之间的关系,由此你有什么结论吗
A
结论:两边和它们的夹角对应相等的三角形全等.简记为“边角边”或“SAS”。
三角形全等判定方法1:
用数学语言表述:
在△ABC与△DEF中,
AB=DE,
∠B=∠E,
BC=EF,
所以△ABC≌△DEF(SAS)。
A
B
C
D
E
F
两边和它们的夹角对应相等的两个三角形全等(简写成“边角边”或“SAS”)。
如图, AB=CB ,∠ ABD= ∠ CBD ,
△ ABD 和△ CBD 全等吗?
例1
证明:
所以△ ABD ≌△ CBD(SAS).
边:
角:
边:
AB=CB(已知),
∠ABD= ∠CBD(已知),
BD=BD(公共边),
A
B
C
D
在△ ABD 和△ CBD中,
范例学习
活 动 三
下列图形中,若用SAS证两个三角形全等,至少还需要添加什么条件
如果AB之间不能直接测量,你能测出AB之间的距离吗
A
B
C
D
O
D
C
A
B
范例学习
例2 如图,在湖泊的岸边有A、B两点,难以直接量出A、B两点间的距离.学习了边角边后,聪明的小杰说他会测量了.你知道他是怎么做的吗 为什么可以这样做
A
B
C
A′
B′
因为△ABC≌△A′B′C′ , (SAS) 所以AB=A′B′ .(全等三角形的对应边相等) 所以A′B′的长度就是A、B两点之间的距离.
解:在岸上取可以直接到达A、B的一点C,连接AC,延长AC到点A′,使A′C=AC;连接BC到点B′,使B′C=BC.连接A′B′,量出A′B′的长度.
范例学习
例3 已知:如图,AD∥BC,AD=BC,
求证:△ADC≌△CBA.
证明:∵AD∥BC(已知)
∴∠DAC=∠BCA.(两直线平行,内错角相等)
在△ADC和△CBA中,
AD=BC,(已知)
∠DAC=∠BCA,(已证)
AC=CA,(公共边)
∴△ADC≌△CBA.(SAS)
A
B
C
D
准备条件
指出范围
列举条件
得出结论
牛刀小试
已知:如图,AB=DB,CB=EB,∠1=∠2.
求证:∠A=∠D.
证明:∵∠1=∠2,(已知)
∴∠1+∠DBC=∠2+∠DBC.(等式的性质)
即∠ABC=∠DBE.
在△ABC和△DBE中,
AB=DB,(已知)
∠ABC=∠DBE,(已证)
CB=EB,(已知)
∴△ABC≌△DBE.(SAS)
∴∠A=∠D.(全等三角形的对应角相等)
1
A
2
C
B
D
E
以2.5cm,3.5cm为三角形的两边,长度为2.5cm的边所对的角为40° ,情况又怎样?动手画一画,你发现了什么?
A
B
C
D
E
F
2.5cm
3.5cm
40°
40°
3.5cm
2.5cm
结论:两边及其一边所对的角相等,两个三角形不一定全等
探究
猜一猜:
是不是二条边和一个角对应相等,这样的两个三角形一定全等吗?你能举例说明吗?
如图△ABC与△ABD中,AB=AB,AC=BD, ∠B=∠B
他们全等吗?
B
A
C
D
注:这个角一定要是这两边所夹的角
小 结
1.学习了本节课以后,你有哪些收获
2.你还有什么疑惑
思 考
学习本节课后,我们知道已知两边及其夹角这三对元素对应相等,就可以判断两三角形全等,那么两个三角形具备其他三组元素对应相等,他们是否也能得到两个三角形全等
再 见
