2021-2022学年湘教版九年级上册数学期中复习试卷(Word版,附答案解析)
文档属性
| 名称 | 2021-2022学年湘教版九年级上册数学期中复习试卷(Word版,附答案解析) |  | |
| 格式 | zip | ||
| 文件大小 | 387.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 11:06:49 | ||
图片预览



文档简介
2021-2022学年湘教新版九年级上册数学期中复习试卷
一.选择题(共10小题,满分40分,每小题4分)
1.如图,在平面直角坐标系中,Rt△ABC的顶点A,B分别在y轴、x轴上,OA=2,OB=1,斜边AC∥x轴.若反比例函数y=(k>0,x>0)的图象经过AC的中点D,则k的值为( )
A.4 B.5 C.6 D.8
2.方程(3x﹣2)(x+1)=0的解是( )
A.x= B.x=﹣1
C.x1=﹣,x2=1 D.x1=,x2=﹣1
3.若,则的值为( )
A. B. C. D.
4.已知反比例函数,下列说法中正确的是( )
A.该函数的图象分布在第一、三象限
B.点(﹣4,﹣3)在函数图象上
C.y随x的增大而增大
D.若点(﹣2,y1)和(﹣1,y2)在该函数图象上,则y1<y2
5.下列图形中不一定相似的是( )
A.两个矩形 B.两个圆
C.两个正方形 D.两个等边三角形
6.若一元二次方程(x﹣2)2=9可转化为两个一元一次方程,一个一元一次方程是x﹣2=3,则另一个一元一次方程是( )
A.x﹣2=3 B.x﹣2=﹣3 C.x+2=3 D.x+2=﹣3
7.在函数y=(a为常数)的图象上有三点(﹣3,y1),(﹣1,y2),(2,y3),则函数值y1,y2,y3的大小关系为( )
A.y3<y1<y2 B.y1<y2<y3 C.y3<y2<y1 D.y2<y1<y3
8.若关于x的方程kx2﹣6x+9=0有实数根,则k的取值范围是( )
A.k<1 B.k≤1 C.k<1且k≠0 D.k≤1且k≠0
9.新龟兔赛跑的故事:龟兔从同一地点同时出发后,兔子很快把乌龟远远甩在后头.骄傲自满的兔子觉得自己遥遥领先,就躺在路边呼呼大睡起来.当它一觉醒来,发现乌龟已经超过它,于是奋力直追,最后同时到达终点.用S1、S2分别表示乌龟和兔子赛跑的路程,t为赛跑时间,则下列图象中与故事情节相吻合的是( )
A. B.
C. D.
10.如图,在矩形ABCD中,AB=m,BC=6,点E在边CD上,且CE=m.连接BE,将△BCE沿BE折叠,点C的对应点C'恰好落在边AD上,则m=( )
A.3 B.2 C. D.5
二.填空题(共8小题,满分32分,每小题4分)
11.若函数y=m是反比例函数,则m= .
12.已知a是方程x2﹣2018x+1=0的一个根a,则a2﹣2017a+的值为 .
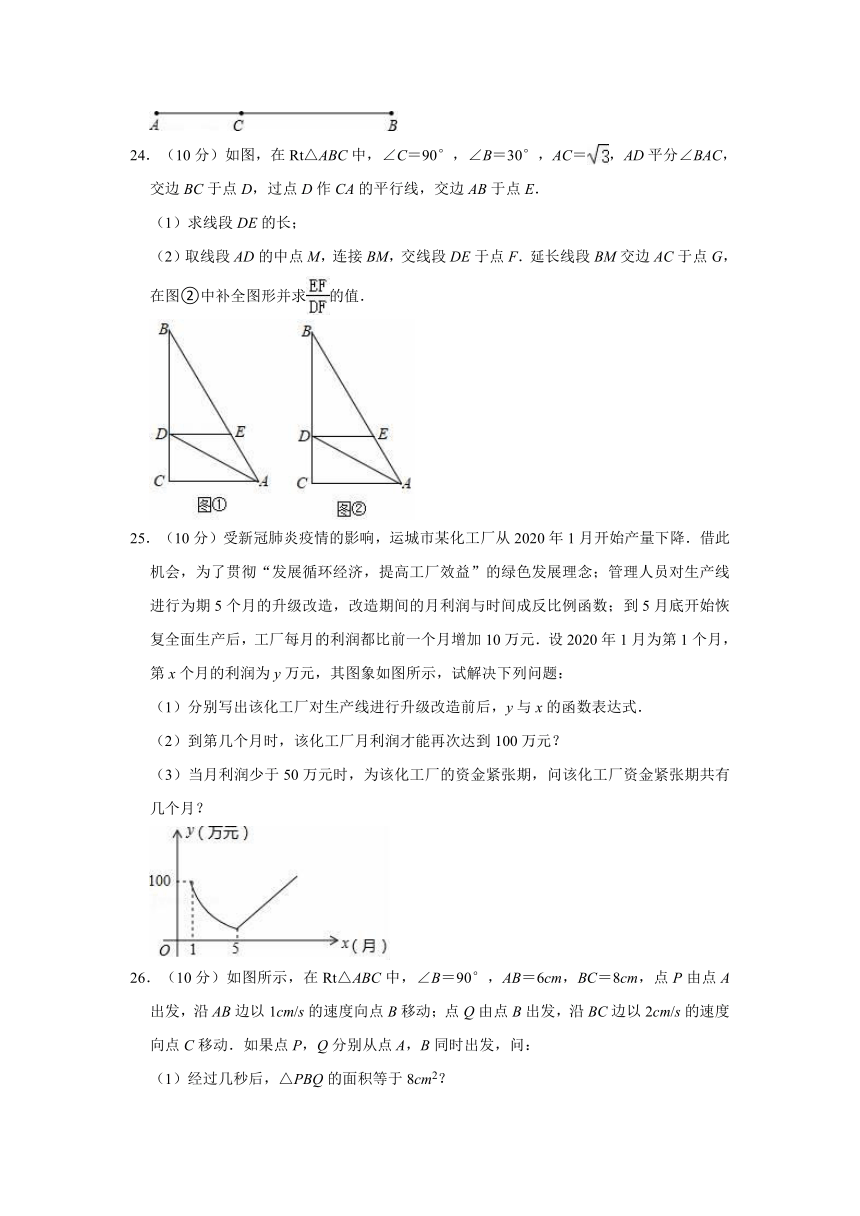
13.《九章算术》中记载了一种测量古井水面以上部分深度的方法.如图所示,在井口A处立一根垂直于井口的木杆AB,从木杆的顶端B观察井水水岸D,视线BD与井口的直径AC交于点E,如果测得AB=1米,AC=1.6米,AE=0.4米,那么CD为 米.
14.反比例函数y=的图象在一、三象限,则m应满足 .
15.已知(m﹣1)x|m+1|+2mx+4=0是关于x的一元二次方程,则m的值是 .
16.如图,直线y=kx+b与双曲线y=相交于A(﹣2,),B(1,﹣3)两点,则不等式kx+b<的解集为 .
17.某超市销售一种饮料,平均每天可售出100箱,每箱利润20元.为扩大销售,增加利润,超市准备适当降价.据测算,每箱每降价4元,平均每天可多售出20箱.若要使每天销售这种饮料获利1280元,每箱应降价多少元?设每箱降价x元,可列方程,得 .
18.如图,在△ABC中,∠C=90°,BC=3,AC=4,D为AB中点.若在AC边上取点E,使△ADE与△ABC相似,则AE的长为 .
三.解答题(共8小题,满分78分)
19.(10分)解下列方程:
(1)(x﹣3)2﹣4=0;
(2)x2﹣4x﹣8=0.
20.(12分)如图,一次函数y1=ax+b与反比例函数y2=的图象相交于A(2,8),B(8,2)两点,连接AO,BO,延长AO交反比例函数图象于点C.
(1)求一次函数y1的表达式与反比例函数y2的表达式;
(2)当y1<y2,时,直接写出自变量x的取值范围为 ;
(3)点P是x轴上一点,当S△PAC=S△AOB时,请直接写出点P的坐标为 .
21.(8分)如图,△ABC中,BD平分∠ABC,E为BC上一点,∠BDE=∠BAD=90°.
(1)求证:BD2=BA BE;
(2)若AB=6,BE=8,求CD的长.
22.(10分)对于实数m、n,定义一种运算:m△n=mn+n.
(1)求﹣2△的值;
(2)如果关于x的方程x△(a△x)=有两个相等的实数根,求实数a的值.
23.(8分)在线段AB上存在一点C,满足AC:CB=CB:AB=k.
(1)求k的值.
(2)如果三条线段a、b、c满足a:b=b:c=k,问这三条线段能否构成三角形,如果能,请指出三角形的形状;如果不能,请说明理由.
24.(10分)如图,在Rt△ABC中,∠C=90°,∠B=30°,AC=,AD平分∠BAC,交边BC于点D,过点D作CA的平行线,交边AB于点E.
(1)求线段DE的长;
(2)取线段AD的中点M,连接BM,交线段DE于点F.延长线段BM交边AC于点G,在图②中补全图形并求的值.
25.(10分)受新冠肺炎疫情的影响,运城市某化工厂从2020年1月开始产量下降.借此机会,为了贯彻“发展循环经济,提高工厂效益”的绿色发展理念;管理人员对生产线进行为期5个月的升级改造,改造期间的月利润与时间成反比例函数;到5月底开始恢复全面生产后,工厂每月的利润都比前一个月增加10万元.设2020年1月为第1个月,第x个月的利润为y万元,其图象如图所示,试解决下列问题:
(1)分别写出该化工厂对生产线进行升级改造前后,y与x的函数表达式.
(2)到第几个月时,该化工厂月利润才能再次达到100万元?
(3)当月利润少于50万元时,为该化工厂的资金紧张期,问该化工厂资金紧张期共有几个月?
26.(10分)如图所示,在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点P由点A出发,沿AB边以1cm/s的速度向点B移动;点Q由点B出发,沿BC边以2cm/s的速度向点C移动.如果点P,Q分别从点A,B同时出发,问:
(1)经过几秒后,△PBQ的面积等于8cm2?
(2)经过几秒后,P,Q两点间距离是cm?
参考答案与试题解析
一.选择题(共10小题,满分40分,每小题4分)
1.解:作CE⊥x轴于E,
∵AC∥x轴,OA=2,OB=1,
∴OA=CE=2,
∵∠ABO+∠CBE=90°=∠OAB+∠ABO,
∴∠OAB=∠CBE,
∵∠AOB=∠BEC,
∴△AOB∽△BEC,
∴=,即=,
∴BE=4,
∴OE=5,
∵点D是AC的中点,
∴D(,2).
∵反比例函数y=(k>0,x>0)的图象经过点D,
∴k=×2=5.
故选:B.
2.解:方程(3x﹣2)(x+1)=0,
可得3x﹣2=0或x+1=0,
解得:x1=,x2=﹣1.
故选:D.
3.解:设===k,
则x=3k,y=4k,z=6k,
所以
=
=
=,
故选:A.
4.解:A、k=﹣6<0,函数的图象在第二、四象限,故说法错误;
B、因为﹣3×(﹣4)=12≠﹣6,所以点(﹣4,﹣3)不在函数图象上,故说法错误
C、k=﹣6<0,在每个象限内,y随着x的增大而增大,故说法错误;
D、k=﹣6<0,在每个象限内,y随着x的增大而增大,因为﹣2<﹣1<0,则y1<y2,故说法正确;
故选:D.
5.解:A.所有的矩形,对应边不一定成比例,对应角一定相等,故不一定相似,故本选项符合题意;
B.所有的圆,一定相似,故本选项不合题意;
C.所有的正方形对应边成比例,对应角相等,一定相似,故本选项不合题意;
D.所有的等边三角形对应边成比例,对应角相等,一定相似,故本选项不合题意.
故选:A.
6.解:原方程两边开方可得:x﹣2=±3,
即x﹣2=3或x﹣2=﹣3,
故选:B.
7.解:∵﹣a2﹣1<0,
∴函数y=(a为常数)的图象在二、四象限,且在每一象限内y随x的增大而增大,
∵﹣3<﹣1<0,
∴点(﹣3,y1),(﹣1,y2)在第二象限,
∴y2>y1>0,
∵2>0,
∴点(2,y3)在第四象限,
∴y3<0,
∴y3<y1<y2.
故选:A.
8.解:(1)当k=0时,﹣6x+9=0,解得x=;
(2)当k≠0时,此方程是一元二次方程,
∵关于x的方程kx2﹣6x+9=0有实数根,
∴Δ=(﹣6)2﹣4k×9≥0,解得k≤1,
由(1)、(2)得,k的取值范围是k≤1.
故选:B.
9.解:A.此函数图象中,S2先达到最大值,即兔子先到终点,不符合题意;
B.此函数图象中,S2第2段随时间增加其路程一直保持不变,与“当它一觉醒来,发现乌龟已经超过它,于是奋力直追”不符,不符合题意;
C.此函数图象中,乌龟和兔子同时到达终点,符合题意;
D.此函数图象中,S1先达到最大值,即乌龟先到终点,不符合题意.
故选:C.
10.解:∵四边形ABCD是矩形,
∴AD=BC=6,CD=AB=m,∠A=∠D=∠C=90°.
∵将△BCE沿BE折叠,点C的对应点C'恰好落在边AD上,
∴BC'=BC=6,∠BC'E=∠C=90°,C'E=CE=m,DE=CD﹣CE=m﹣m=m,
∴DE=C'E,
∴∠DC'E=30°,
∴∠AC'B=180°﹣90°﹣30°=60°,
∴AB=BC'×sin∠AC'B=6×=3,
即m=3;
故选:A.
二.填空题(共8小题,满分32分,每小题4分)
11.解:∵函数y=m是反比例函数,
∴m2+3m﹣1=﹣1,m≠0,
解得:m=﹣3.
故答案为:﹣3.
12.解:根据题意可知:a2﹣2018a+1=0,
∴a2+1=2018a,
a2﹣2017a=a﹣1,
∴原式=a2﹣2017a+
=a﹣1+
=﹣1
=2018﹣1
=2017
故答案为:2017
13.解:由题意知:AB∥CD,
则∠BAE=∠C,∠B=∠CDE,
∴△ABE∽△CDE,
∴,
∴,
∴CD=3米,
故答案为:3.
14.解:∵反比例函数y=的图象在一、三象限,
∴m﹣3>0,
解得m>3.
故答案为:m>3.
15.解:∵(m﹣1)x|m+1|+2mx+4=0是关于x的一元二次方程,
∴|m+1|=2,m﹣1≠0,
解得:m=﹣3,
故答案为:﹣3.
16.解:∵两函数的交点A和B的横坐标分别为﹣2和1,
∴当﹣2<x<0或x>1时,一次函数图象在反比例函数图象下方,
∴不等式kx+b<的解集为﹣2<x<0或x>1,
故答案为﹣2<x<0或x>1.
17.解:设每箱应降价x元,则销售数量为:(100+×20)箱,
根据题意,得(20﹣x)(100+×20)=1280,
故答案是:(20﹣x)(100+×20)=1280.
18.解:∵∠C=90°,AC=4,BC=3,
∴AB===5,
∵D为AB的中点,
∴AD=AB=,
当△ADE∽△ABC时,,即,
解得,AE=2,
当△ADE∽△ACB时,,即,
解得,AE=,
故答案为:2或.
三.解答题(共8小题,满分78分)
19.解:(1)∵(x﹣3)2=4,
∴x﹣3=2或x﹣3=﹣2,
解得x1=5,x2=1;
(2)∵x2﹣4x﹣8=0,
∴x2﹣4x=8,
则x2﹣4x+4=8+4,即(x﹣2)2=12,
∴x﹣2=,
∴x1=2+2,x2=2﹣2.
20.解:(1)将A(2,8),B(8,2)代入y=ax+b得,
解得,
∴一次函数为y=﹣x+10,
将A(2,8)代入y2=得8=,解得k=16,
∴反比例函数的解析式为y=;
(2)由图象可知,当y1<y2时,自变量x的取值范围为:x>8或0<x<2,
故答案为x>8或0<x<2;
(3)由题意可知OA=OC,
∴S△APC=2S△AOP,
把y=0代入y1=﹣x+10得,0=﹣x+10,解得x=10,
∴D(10,0),
∴S△AOB=S△AOD﹣S△BOD=﹣=30,
∵S△PAC=S△AOB=×30=24,
∴2S△AOP=24,
∴2××yA=24,即2×OP×8=24,
∴OP=3,
∴P(3,0)或P(﹣3,0),
故答案为P(3,0)或P(﹣3,0).
21.证明:(1)∵BD平分∠ABC,
∴∠ABD=∠CBD,
又∵∠BDE=∠BAD=90°,
∴△ABD∽△DBE,
∴,
∴BD2=BA BE;
(2)∵AB=6,BE=8,BD2=BA BE,
∴BD=4,
∴DE===4,
∵∠BDC=∠A+∠ABD=∠BDE+∠EDC,
∴∠ABD=∠CDE,
∴∠CDE=∠DBC,
又∵∠C=∠C,
∴△BCD∽△DCE,
∴,
∴,
∴EC=4,CD=4.
方法二、∵sin∠DBE===,
∴∠DBE=30°,
∴∠ABD=∠DBE=30°,
∴∠C=30°,
∴∠C=∠DBC,
∴BD=CD,
∵∠ABD=30°,
∴cos∠ABD==
∴BD=4,
∴CD=4.
22.解:(1)﹣2△=﹣2×+=﹣2×4+4=﹣4;
(2)∵a△x=ax+x,
∴x△(a△x)=x(ax+x)+ax+x,
∴关于x的方程x△(a△x)=化为x(ax+x)+ax+x=﹣,
整理得(a+1)x2+(a+1)x+=0,
∵方程有两个相等的实数根,
∴a+1≠0且Δ=(a+1)2﹣4(a+1)×=0,解得a=0,
即a的值为0.
23.解:(1)因为AC:CB=CB:AB=k,不妨设AB=1,则
CB=k,AC=k2.
又∵AC+BC=AB,
∴k2+k=1,
∴.
又因为k>0,
∴.
(2)因为a:b=b:c=k,
所以,
∴a+b=c.
所以线段a、b、c不能构成三角形.
24.解:(1)∵AD平分∠BAC,∠BAC=60°,
∴∠DAC=30°,
在Rt△ACD中,∠ACD=90°,∠DAC=30°,AC=,
∴CD=1,
在Rt△ACB中,∠ACB=90°,∠BAC=60°,
∴BC=3,
∴BD=BC﹣CD=2,
∵DE∥CA,
∴△BDE∽△BCA,
∴=,
∴DE=;
(2)如图,
∵点M是线段AD的中点,
∴DM=AM,
∵DE∥CA,
∴,
∴DF=AG,
∵DE∥CA,
∴,,
∴,
∵BD=2,BC=3,DF=AG,
∴.
25.解:(1)(0<x≤5,且x为整数)y=10x﹣30(x>5且x为整数).
(2)在函数y=10x﹣30中,令y=100,得10x﹣30=100,
解得:x=13,
答:到第13个月时,该化工厂月利润再次达到100万元.
(3)在函数中,
当y=50时,x=2,
∵100>0,y随x的增大而减小,
∴当y<50时,x>2,
在函数y=10x﹣30中,
当y<50时,得10x﹣30<50
解得:x<8
∴2<x<8且x为整数;
∴x可取3,4,5,6,7;共5个月.
答:该化工厂资金紧张期共有5个月.
26.解:(1)设经过x秒后,△PBQ的面积等于8cm2,则BP=(6﹣x)cm,BQ=2xcm,
依题意,得:(6﹣x)×2x=8,
化简,得:x2﹣6x+8=0,
解得:x1=2,x2=4.
答:经过2秒或4秒后,△PBQ的面积等于8cm2.
(2)设经过y秒后,P,Q两点间距离是cm,则BP=(6﹣y)cm,BQ=2ycm,
依题意,得:(6﹣y)2+(2y)2=()2,
化简,得:5y2﹣12y﹣17=0,
解得:y1=,y2=﹣1(不合题意,舍去).
答:经过秒后,P,Q两点间距离是cm.
一.选择题(共10小题,满分40分,每小题4分)
1.如图,在平面直角坐标系中,Rt△ABC的顶点A,B分别在y轴、x轴上,OA=2,OB=1,斜边AC∥x轴.若反比例函数y=(k>0,x>0)的图象经过AC的中点D,则k的值为( )
A.4 B.5 C.6 D.8
2.方程(3x﹣2)(x+1)=0的解是( )
A.x= B.x=﹣1
C.x1=﹣,x2=1 D.x1=,x2=﹣1
3.若,则的值为( )
A. B. C. D.
4.已知反比例函数,下列说法中正确的是( )
A.该函数的图象分布在第一、三象限
B.点(﹣4,﹣3)在函数图象上
C.y随x的增大而增大
D.若点(﹣2,y1)和(﹣1,y2)在该函数图象上,则y1<y2
5.下列图形中不一定相似的是( )
A.两个矩形 B.两个圆
C.两个正方形 D.两个等边三角形
6.若一元二次方程(x﹣2)2=9可转化为两个一元一次方程,一个一元一次方程是x﹣2=3,则另一个一元一次方程是( )
A.x﹣2=3 B.x﹣2=﹣3 C.x+2=3 D.x+2=﹣3
7.在函数y=(a为常数)的图象上有三点(﹣3,y1),(﹣1,y2),(2,y3),则函数值y1,y2,y3的大小关系为( )
A.y3<y1<y2 B.y1<y2<y3 C.y3<y2<y1 D.y2<y1<y3
8.若关于x的方程kx2﹣6x+9=0有实数根,则k的取值范围是( )
A.k<1 B.k≤1 C.k<1且k≠0 D.k≤1且k≠0
9.新龟兔赛跑的故事:龟兔从同一地点同时出发后,兔子很快把乌龟远远甩在后头.骄傲自满的兔子觉得自己遥遥领先,就躺在路边呼呼大睡起来.当它一觉醒来,发现乌龟已经超过它,于是奋力直追,最后同时到达终点.用S1、S2分别表示乌龟和兔子赛跑的路程,t为赛跑时间,则下列图象中与故事情节相吻合的是( )
A. B.
C. D.
10.如图,在矩形ABCD中,AB=m,BC=6,点E在边CD上,且CE=m.连接BE,将△BCE沿BE折叠,点C的对应点C'恰好落在边AD上,则m=( )
A.3 B.2 C. D.5
二.填空题(共8小题,满分32分,每小题4分)
11.若函数y=m是反比例函数,则m= .
12.已知a是方程x2﹣2018x+1=0的一个根a,则a2﹣2017a+的值为 .
13.《九章算术》中记载了一种测量古井水面以上部分深度的方法.如图所示,在井口A处立一根垂直于井口的木杆AB,从木杆的顶端B观察井水水岸D,视线BD与井口的直径AC交于点E,如果测得AB=1米,AC=1.6米,AE=0.4米,那么CD为 米.
14.反比例函数y=的图象在一、三象限,则m应满足 .
15.已知(m﹣1)x|m+1|+2mx+4=0是关于x的一元二次方程,则m的值是 .
16.如图,直线y=kx+b与双曲线y=相交于A(﹣2,),B(1,﹣3)两点,则不等式kx+b<的解集为 .
17.某超市销售一种饮料,平均每天可售出100箱,每箱利润20元.为扩大销售,增加利润,超市准备适当降价.据测算,每箱每降价4元,平均每天可多售出20箱.若要使每天销售这种饮料获利1280元,每箱应降价多少元?设每箱降价x元,可列方程,得 .
18.如图,在△ABC中,∠C=90°,BC=3,AC=4,D为AB中点.若在AC边上取点E,使△ADE与△ABC相似,则AE的长为 .
三.解答题(共8小题,满分78分)
19.(10分)解下列方程:
(1)(x﹣3)2﹣4=0;
(2)x2﹣4x﹣8=0.
20.(12分)如图,一次函数y1=ax+b与反比例函数y2=的图象相交于A(2,8),B(8,2)两点,连接AO,BO,延长AO交反比例函数图象于点C.
(1)求一次函数y1的表达式与反比例函数y2的表达式;
(2)当y1<y2,时,直接写出自变量x的取值范围为 ;
(3)点P是x轴上一点,当S△PAC=S△AOB时,请直接写出点P的坐标为 .
21.(8分)如图,△ABC中,BD平分∠ABC,E为BC上一点,∠BDE=∠BAD=90°.
(1)求证:BD2=BA BE;
(2)若AB=6,BE=8,求CD的长.
22.(10分)对于实数m、n,定义一种运算:m△n=mn+n.
(1)求﹣2△的值;
(2)如果关于x的方程x△(a△x)=有两个相等的实数根,求实数a的值.
23.(8分)在线段AB上存在一点C,满足AC:CB=CB:AB=k.
(1)求k的值.
(2)如果三条线段a、b、c满足a:b=b:c=k,问这三条线段能否构成三角形,如果能,请指出三角形的形状;如果不能,请说明理由.
24.(10分)如图,在Rt△ABC中,∠C=90°,∠B=30°,AC=,AD平分∠BAC,交边BC于点D,过点D作CA的平行线,交边AB于点E.
(1)求线段DE的长;
(2)取线段AD的中点M,连接BM,交线段DE于点F.延长线段BM交边AC于点G,在图②中补全图形并求的值.
25.(10分)受新冠肺炎疫情的影响,运城市某化工厂从2020年1月开始产量下降.借此机会,为了贯彻“发展循环经济,提高工厂效益”的绿色发展理念;管理人员对生产线进行为期5个月的升级改造,改造期间的月利润与时间成反比例函数;到5月底开始恢复全面生产后,工厂每月的利润都比前一个月增加10万元.设2020年1月为第1个月,第x个月的利润为y万元,其图象如图所示,试解决下列问题:
(1)分别写出该化工厂对生产线进行升级改造前后,y与x的函数表达式.
(2)到第几个月时,该化工厂月利润才能再次达到100万元?
(3)当月利润少于50万元时,为该化工厂的资金紧张期,问该化工厂资金紧张期共有几个月?
26.(10分)如图所示,在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点P由点A出发,沿AB边以1cm/s的速度向点B移动;点Q由点B出发,沿BC边以2cm/s的速度向点C移动.如果点P,Q分别从点A,B同时出发,问:
(1)经过几秒后,△PBQ的面积等于8cm2?
(2)经过几秒后,P,Q两点间距离是cm?
参考答案与试题解析
一.选择题(共10小题,满分40分,每小题4分)
1.解:作CE⊥x轴于E,
∵AC∥x轴,OA=2,OB=1,
∴OA=CE=2,
∵∠ABO+∠CBE=90°=∠OAB+∠ABO,
∴∠OAB=∠CBE,
∵∠AOB=∠BEC,
∴△AOB∽△BEC,
∴=,即=,
∴BE=4,
∴OE=5,
∵点D是AC的中点,
∴D(,2).
∵反比例函数y=(k>0,x>0)的图象经过点D,
∴k=×2=5.
故选:B.
2.解:方程(3x﹣2)(x+1)=0,
可得3x﹣2=0或x+1=0,
解得:x1=,x2=﹣1.
故选:D.
3.解:设===k,
则x=3k,y=4k,z=6k,
所以
=
=
=,
故选:A.
4.解:A、k=﹣6<0,函数的图象在第二、四象限,故说法错误;
B、因为﹣3×(﹣4)=12≠﹣6,所以点(﹣4,﹣3)不在函数图象上,故说法错误
C、k=﹣6<0,在每个象限内,y随着x的增大而增大,故说法错误;
D、k=﹣6<0,在每个象限内,y随着x的增大而增大,因为﹣2<﹣1<0,则y1<y2,故说法正确;
故选:D.
5.解:A.所有的矩形,对应边不一定成比例,对应角一定相等,故不一定相似,故本选项符合题意;
B.所有的圆,一定相似,故本选项不合题意;
C.所有的正方形对应边成比例,对应角相等,一定相似,故本选项不合题意;
D.所有的等边三角形对应边成比例,对应角相等,一定相似,故本选项不合题意.
故选:A.
6.解:原方程两边开方可得:x﹣2=±3,
即x﹣2=3或x﹣2=﹣3,
故选:B.
7.解:∵﹣a2﹣1<0,
∴函数y=(a为常数)的图象在二、四象限,且在每一象限内y随x的增大而增大,
∵﹣3<﹣1<0,
∴点(﹣3,y1),(﹣1,y2)在第二象限,
∴y2>y1>0,
∵2>0,
∴点(2,y3)在第四象限,
∴y3<0,
∴y3<y1<y2.
故选:A.
8.解:(1)当k=0时,﹣6x+9=0,解得x=;
(2)当k≠0时,此方程是一元二次方程,
∵关于x的方程kx2﹣6x+9=0有实数根,
∴Δ=(﹣6)2﹣4k×9≥0,解得k≤1,
由(1)、(2)得,k的取值范围是k≤1.
故选:B.
9.解:A.此函数图象中,S2先达到最大值,即兔子先到终点,不符合题意;
B.此函数图象中,S2第2段随时间增加其路程一直保持不变,与“当它一觉醒来,发现乌龟已经超过它,于是奋力直追”不符,不符合题意;
C.此函数图象中,乌龟和兔子同时到达终点,符合题意;
D.此函数图象中,S1先达到最大值,即乌龟先到终点,不符合题意.
故选:C.
10.解:∵四边形ABCD是矩形,
∴AD=BC=6,CD=AB=m,∠A=∠D=∠C=90°.
∵将△BCE沿BE折叠,点C的对应点C'恰好落在边AD上,
∴BC'=BC=6,∠BC'E=∠C=90°,C'E=CE=m,DE=CD﹣CE=m﹣m=m,
∴DE=C'E,
∴∠DC'E=30°,
∴∠AC'B=180°﹣90°﹣30°=60°,
∴AB=BC'×sin∠AC'B=6×=3,
即m=3;
故选:A.
二.填空题(共8小题,满分32分,每小题4分)
11.解:∵函数y=m是反比例函数,
∴m2+3m﹣1=﹣1,m≠0,
解得:m=﹣3.
故答案为:﹣3.
12.解:根据题意可知:a2﹣2018a+1=0,
∴a2+1=2018a,
a2﹣2017a=a﹣1,
∴原式=a2﹣2017a+
=a﹣1+
=﹣1
=2018﹣1
=2017
故答案为:2017
13.解:由题意知:AB∥CD,
则∠BAE=∠C,∠B=∠CDE,
∴△ABE∽△CDE,
∴,
∴,
∴CD=3米,
故答案为:3.
14.解:∵反比例函数y=的图象在一、三象限,
∴m﹣3>0,
解得m>3.
故答案为:m>3.
15.解:∵(m﹣1)x|m+1|+2mx+4=0是关于x的一元二次方程,
∴|m+1|=2,m﹣1≠0,
解得:m=﹣3,
故答案为:﹣3.
16.解:∵两函数的交点A和B的横坐标分别为﹣2和1,
∴当﹣2<x<0或x>1时,一次函数图象在反比例函数图象下方,
∴不等式kx+b<的解集为﹣2<x<0或x>1,
故答案为﹣2<x<0或x>1.
17.解:设每箱应降价x元,则销售数量为:(100+×20)箱,
根据题意,得(20﹣x)(100+×20)=1280,
故答案是:(20﹣x)(100+×20)=1280.
18.解:∵∠C=90°,AC=4,BC=3,
∴AB===5,
∵D为AB的中点,
∴AD=AB=,
当△ADE∽△ABC时,,即,
解得,AE=2,
当△ADE∽△ACB时,,即,
解得,AE=,
故答案为:2或.
三.解答题(共8小题,满分78分)
19.解:(1)∵(x﹣3)2=4,
∴x﹣3=2或x﹣3=﹣2,
解得x1=5,x2=1;
(2)∵x2﹣4x﹣8=0,
∴x2﹣4x=8,
则x2﹣4x+4=8+4,即(x﹣2)2=12,
∴x﹣2=,
∴x1=2+2,x2=2﹣2.
20.解:(1)将A(2,8),B(8,2)代入y=ax+b得,
解得,
∴一次函数为y=﹣x+10,
将A(2,8)代入y2=得8=,解得k=16,
∴反比例函数的解析式为y=;
(2)由图象可知,当y1<y2时,自变量x的取值范围为:x>8或0<x<2,
故答案为x>8或0<x<2;
(3)由题意可知OA=OC,
∴S△APC=2S△AOP,
把y=0代入y1=﹣x+10得,0=﹣x+10,解得x=10,
∴D(10,0),
∴S△AOB=S△AOD﹣S△BOD=﹣=30,
∵S△PAC=S△AOB=×30=24,
∴2S△AOP=24,
∴2××yA=24,即2×OP×8=24,
∴OP=3,
∴P(3,0)或P(﹣3,0),
故答案为P(3,0)或P(﹣3,0).
21.证明:(1)∵BD平分∠ABC,
∴∠ABD=∠CBD,
又∵∠BDE=∠BAD=90°,
∴△ABD∽△DBE,
∴,
∴BD2=BA BE;
(2)∵AB=6,BE=8,BD2=BA BE,
∴BD=4,
∴DE===4,
∵∠BDC=∠A+∠ABD=∠BDE+∠EDC,
∴∠ABD=∠CDE,
∴∠CDE=∠DBC,
又∵∠C=∠C,
∴△BCD∽△DCE,
∴,
∴,
∴EC=4,CD=4.
方法二、∵sin∠DBE===,
∴∠DBE=30°,
∴∠ABD=∠DBE=30°,
∴∠C=30°,
∴∠C=∠DBC,
∴BD=CD,
∵∠ABD=30°,
∴cos∠ABD==
∴BD=4,
∴CD=4.
22.解:(1)﹣2△=﹣2×+=﹣2×4+4=﹣4;
(2)∵a△x=ax+x,
∴x△(a△x)=x(ax+x)+ax+x,
∴关于x的方程x△(a△x)=化为x(ax+x)+ax+x=﹣,
整理得(a+1)x2+(a+1)x+=0,
∵方程有两个相等的实数根,
∴a+1≠0且Δ=(a+1)2﹣4(a+1)×=0,解得a=0,
即a的值为0.
23.解:(1)因为AC:CB=CB:AB=k,不妨设AB=1,则
CB=k,AC=k2.
又∵AC+BC=AB,
∴k2+k=1,
∴.
又因为k>0,
∴.
(2)因为a:b=b:c=k,
所以,
∴a+b=c.
所以线段a、b、c不能构成三角形.
24.解:(1)∵AD平分∠BAC,∠BAC=60°,
∴∠DAC=30°,
在Rt△ACD中,∠ACD=90°,∠DAC=30°,AC=,
∴CD=1,
在Rt△ACB中,∠ACB=90°,∠BAC=60°,
∴BC=3,
∴BD=BC﹣CD=2,
∵DE∥CA,
∴△BDE∽△BCA,
∴=,
∴DE=;
(2)如图,
∵点M是线段AD的中点,
∴DM=AM,
∵DE∥CA,
∴,
∴DF=AG,
∵DE∥CA,
∴,,
∴,
∵BD=2,BC=3,DF=AG,
∴.
25.解:(1)(0<x≤5,且x为整数)y=10x﹣30(x>5且x为整数).
(2)在函数y=10x﹣30中,令y=100,得10x﹣30=100,
解得:x=13,
答:到第13个月时,该化工厂月利润再次达到100万元.
(3)在函数中,
当y=50时,x=2,
∵100>0,y随x的增大而减小,
∴当y<50时,x>2,
在函数y=10x﹣30中,
当y<50时,得10x﹣30<50
解得:x<8
∴2<x<8且x为整数;
∴x可取3,4,5,6,7;共5个月.
答:该化工厂资金紧张期共有5个月.
26.解:(1)设经过x秒后,△PBQ的面积等于8cm2,则BP=(6﹣x)cm,BQ=2xcm,
依题意,得:(6﹣x)×2x=8,
化简,得:x2﹣6x+8=0,
解得:x1=2,x2=4.
答:经过2秒或4秒后,△PBQ的面积等于8cm2.
(2)设经过y秒后,P,Q两点间距离是cm,则BP=(6﹣y)cm,BQ=2ycm,
依题意,得:(6﹣y)2+(2y)2=()2,
化简,得:5y2﹣12y﹣17=0,
解得:y1=,y2=﹣1(不合题意,舍去).
答:经过秒后,P,Q两点间距离是cm.
同课章节目录
