2021-2022学年冀教新版八年级上册数学期中复习试卷(word解析版)
文档属性
| 名称 | 2021-2022学年冀教新版八年级上册数学期中复习试卷(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 322.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 12:43:48 | ||
图片预览


文档简介
2021-2022学年冀教新版八年级上册数学期中复习试卷
一.选择题(共16小题,满分32分,每小题2分)
1.在、、、、、中,分式的个数有( )
A.2个 B.3个 C.4个 D.5个
2.下列实数:15,,,﹣3π,0.10101中,无理数有( )个.
A.1 B.2 C.3 D.4
3.如图,AB,CD表示两根长度相等的铁条,若O是AB,CD的中点,经测量AC=15cm,则容器的内径长为( )
A.12cm B.13cm C.14cm D.15cm
4.若分式在实数范围内有意义,则x的取值范围是( )
A.x≠﹣5 B.x≠0 C.x≠5 D.x>﹣5
5.如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
A.∠A=∠D B.AB=DC C.∠ACB=∠DBC D.AC=BD
6.下列分式中,与的值相等的是( )
A. B. C.﹣ D.
7.一个数的两个平方根分别是2a﹣1与﹣a+2,则这个数是( )
A.﹣1 B.3 C.9 D.﹣3
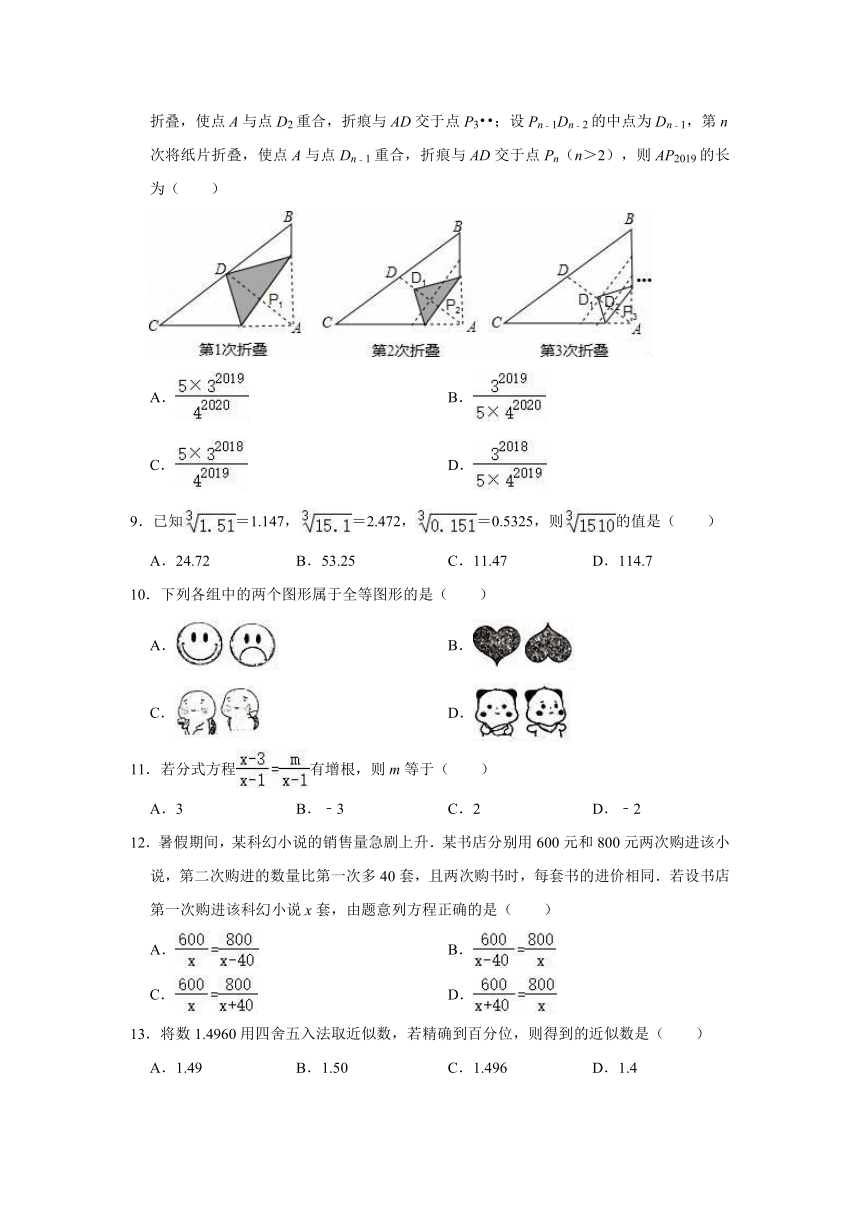
8.如图,直角三角形纸片ABC中,AB=3,AC=4.D为斜边BC的中点,第1次将纸片折叠,使点A与点D重合,折痕与AD交于点P1;设P1D的中点为D1,第2次将纸片折叠,使点A与点D1重合,折痕与AD交于点P2;设P2D1的中点为D2,第3次将纸片折叠,使点A与点D2重合,折痕与AD交于点P3 ;设Pn﹣1Dn﹣2的中点为Dn﹣1,第n次将纸片折叠,使点A与点Dn﹣1重合,折痕与AD交于点Pn(n>2),则AP2019的长为( )
A. B.
C. D.
9.已知=1.147,=2.472,=0.5325,则的值是( )
A.24.72 B.53.25 C.11.47 D.114.7
10.下列各组中的两个图形属于全等图形的是( )
A. B.
C. D.
11.若分式方程有增根,则m等于( )
A.3 B.﹣3 C.2 D.﹣2
12.暑假期间,某科幻小说的销售量急剧上升.某书店分别用600元和800元两次购进该小说,第二次购进的数量比第一次多40套,且两次购书时,每套书的进价相同.若设书店第一次购进该科幻小说x套,由题意列方程正确的是( )
A. B.
C. D.
13.将数1.4960用四舍五入法取近似数,若精确到百分位,则得到的近似数是( )
A.1.49 B.1.50 C.1.496 D.1.4
14.化简+的结果是( )
A.x B.﹣x C.x﹣1 D.x+1
15.下列说法正确的是( )
A.形状相同的两个三角形全等
B.面积相等的两个三角形全等
C.完全重合的两个三角形全等
D.所有的等边三角形全等
16.如图,已知线段AB=18米,MA⊥AB于点A,MA=6米,射线BD⊥AB于B,P点从B点向A运动,每秒走1米,Q点从B点向D运动,每秒走2米,P、Q同时从B出发,则出发x秒后,在线段MA上有一点C,使△CAP与△PBQ全等,则x的值为( )
A.4 B.6 C.4或9 D.6或9
二.填空题(共4小题,满分12分,每小题3分)
17.如果一个正数a的两个不同平方根分别是2x﹣2和6﹣3x,则a= .
18.如果表示a、b的实数的点在数轴上的位置如图所示,那么化简|a﹣b|+的结果是 .
19.已知关于x的方程的解是正数,则m的取值范围为 .
20.如图,在四边形ABCD中,∠B=∠C=45°,P是BC上一点,PA=PD,∠APD=90°,= .
三.解答题(共6小题,满分56分)
21.(9分)解方程.
(1)求x的值:(x﹣3)2=16.
(2)﹣=1.
22.(9分)(1)解不等式组,并写出它的整数解.
(2)先化简,再求值:( +)÷,其中m=4.
23.(9分)比较与的大小.
24.(9分)如图,AB=AC,直线l过点A,BM⊥直线l,CN⊥直线l,垂足分别为M、N,且BM=AN.
(1)求证△AMB≌△CNA;
(2)求证∠BAC=90°.
25.(10分)某超市在2017年“双11”,销售一批用16800元购进的中老年人保暖内衣,发现供不应求.为了备战“双12”,积极参与支付宝扫码领红包活动,超市又用36400元购进了第二批这种保暖内衣,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该超市购进的第一批保暖内衣是多少件?
(2)两批保暖内衣按相同的标价销售,最后剩下的50件按六折优惠卖出,两批保暖内衣全部售完后利润没有低于进价的20%(不考虑其他因素),请计算每件保暖内衣的标价至少是多少元?
26.(10分)阅读下面材料:
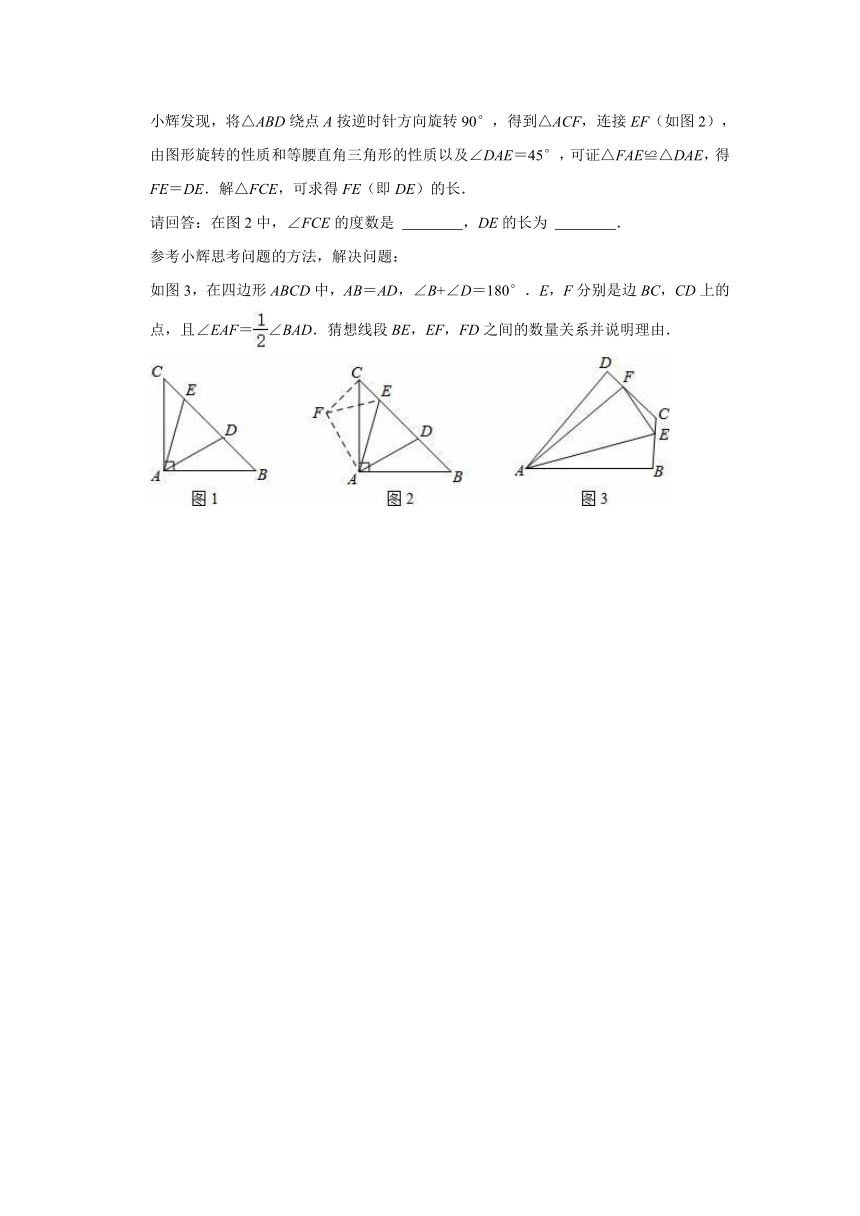
小辉遇到这样一个问题:如图1,在Rt△ABC中,∠BAC=90°,AB=AC,点D,E在边BC上,∠DAE=45°.若BD=3,CE=1,求DE的长.
小辉发现,将△ABD绕点A按逆时针方向旋转90°,得到△ACF,连接EF(如图2),由图形旋转的性质和等腰直角三角形的性质以及∠DAE=45°,可证△FAE≌△DAE,得FE=DE.解△FCE,可求得FE(即DE)的长.
请回答:在图2中,∠FCE的度数是 ,DE的长为 .
参考小辉思考问题的方法,解决问题:
如图3,在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是边BC,CD上的点,且∠EAF=∠BAD.猜想线段BE,EF,FD之间的数量关系并说明理由.
参考答案与试题解析
一.选择题(共16小题,满分32分,每小题2分)
1.解:由题可得,分式有:、、,共3个.
故选:B.
2.解:15 是整数,属于有理数;
是分数,属于有理数;
0.10101是有限小数,属于有理数;
无理数有,﹣3π,共2个,
故选:B.
3.解:∵O是AB,CD的中点,AB=CD,
∴OA=OB=OD=OC,
在△AOC和△BOD中,
,
∴△AOC≌△BOD,
∴AC=BD=15cm,
故选:D.
4.解:根据分式成立的条件,可得:x+5≠0,
∴x≠﹣5,
故选:A.
5.解:A、添加∠A=∠D可利用AAS判定△ABC≌△DCB,故此选项不合题意;
B、添加AB=DC可利用SAS定理判定△ABC≌△DCB,故此选项不合题意;
C、添加∠ACB=∠DBC可利用ASA定理判定△ABC≌△DCB,故此选项不合题意;
D、添加AC=BD不能判定△ABC≌△DCB,故此选项符合题意;
故选:D.
6.解:=﹣=.
故选:D.
7.解:由题意得,
2a﹣1﹣a+2=0,
解得a=﹣1,
所以2a﹣1=﹣3,﹣a+2=3,
即一个数的两个平方根分别是3与﹣3,
所以这个数是9,
故选:C.
8.解:由题意得,AD=BC=,
AD1=AD﹣DD1=,
AD2=,
AD3=,…,
ADn=,
又∵AP1=AD1,AP2=AD2…,∴APn=ADn,
∴AP3==,APn=,
故AP2019的长为:.
故选:C.
9.解:==1.147×10=11.47.
故选:C.
10.解:A、两个图形不能完全重合,故本选项错误;
B、两个图形能够完全重合,故本选项正确;
C、两个图形不能完全重合,故本选项错误;
D、两个图形不能完全重合,故本选项错误;
故选:B.
11.解:分式方程去分母得:x﹣3=m,
由分式方程有增根,得到x﹣1=0,即x=1,
把x=1代入整式方程得:m=﹣2,
故选:D.
12.解:若设书店第一次购进该科幻小说x套,
由题意列方程正确的是,
故选:C.
13.解:1.4960≈1.50(精确到百分位),
故选:B.
14.解:原式=,
故选:A.
15.解:A、形状相同的两个三角形全等,说法错误,应该是形状相同且大小也相同的两个三角形全等;
B、面积相等的两个三角形全等,说法错误;
C、完全重合的两个三角形全等,说法正确;
D、所有的等边三角形全等,说法错误;
故选:C.
16.解:当△APC≌△BQP时,AP=BQ,即18﹣x=2x,
解得:x=6;
当△APC≌△BPQ时,AP=BP=AB=9米,
此时所用时间为9秒,AC=BQ=18米,不合题意,舍去;
综上,出发6秒后,在线段MA上有一点C,使△CAP与△PBQ全等.
故选:B.
二.填空题(共4小题,满分12分,每小题3分)
17.解:因为一个正数a的两个不同平方根分别是2x﹣2和6﹣3x,
所以2x﹣2+6﹣3x=0,
解得x=4,
于是2x﹣2=6,6﹣3x=﹣6,
即一个正数a的两个不同平方根分别是6和﹣6,
所以这个正数a的值为36,
故答案为:36.
18.解:由题意得
|a﹣b|+=a﹣b+[﹣(a+b)]
=a﹣b﹣a﹣b
=﹣2b.
故答案为:﹣2b.
19.解:分式方程去分母得:2x﹣m=x﹣1,
解得:x=m﹣1,
由分式方程的解为正数,得到m﹣1>0,且m﹣1≠1,
解得:m>1且m≠2,
故答案为:m>1且m≠2.
20.解:过点A作AE⊥BC于E,过点D作DF⊥BC于F,
由(1)可知,EF=AE+DF,
∵∠B=∠C=45°,AE⊥BC,DF⊥BC,
∴∠B=∠BAE=45°,∠C=∠CDF=45°,
∴BE=AE,CF=DF,AB=AE,CD=DF,
∴BC=BE+EF+CF=2(AE+DF),
∴==.
故答案为:.
三.解答题(共6小题,满分56分)
21.解:(1)∵(x﹣3)2=16,
∴x﹣3=4或x﹣3=﹣4,
解得x1=﹣1,x2=7;
(2)两边都乘以(x+1)(x﹣1),得:(x+1)2﹣4=(x+1)(x﹣1),
解得x=1,
经检验x=1是分式方程的增根,
∴分式方程无解.
22.解:(1),
解不等式①,得:x>﹣,
解不等式②,得:x≤2,
∴不等式组的解集为﹣<x≤2,
∴不等式组的整数解为﹣1、0、1、2;
(2)原式=
=
=,
当m=4时,原式=.
23.解:因为5>4,
所以>2,
所以﹣2>0,
所以﹣=>0,
所以>.
24.证明:(1)∵BM⊥直线l,CN⊥直线l,
∴∠AMB=∠CNA=90°,
在Rt△AMB和Rt△CNA中,
,
∴Rt△AMB≌Rt△CNA(HL);
(2)由(1)得:Rt△AMB≌Rt△CNA,
∴∠BAM=∠ACN,
∵∠CAN+∠ACN=90°,
∴∠CAN+∠BAM=90°,
∴∠BAC=180°﹣90°=90°.
25.解:(1)设该商家购进的第一批保暖内衣是x件.
根据题意,得
解方程,得x=140.
经检验,x=140是原方程的解,且符合题意.
答:该超市购进的第一批保暖内衣是140件.
(2)根据题意可知两次一共购进保暖内衣为3x=3×140=420(件).
设每件保暖内衣的标价y元.
根据题意,得
(420﹣50)y+50×0.6y≥(16800+36400)×(1+20%).
解不等式,得y≥159.6.
答:每件保暖内衣的标价至少是159.6元.
26.解:如图2,∵∠ACF=∠B=45°,
∴∠FCE=∠ACF+∠ACB=45°+45°=90°,
在Rt△EFC中,∵CF=BD=3,CE=1,
∴EF===,
∴DE=,
故答案为90°;;
如图3,
猜想:EF=BE+FD.理由如下:
如图,将△ABE绕点A按逆时针方向旋转,使AB与AD重合,得到△ADG,
∴BE=DG,AE=AG,∠DAG=∠BAE,∠B=∠ADG,
∵∠B+∠ADC=180°,
∴∠ADG+∠ADC=180°,即点F,D,G在同一条直线上,
∵∠DAG=∠BAE,
∴∠GAE=∠BAD,
∵∠EAF=∠BAD,
∴∠GAF=∠EAF,
在△AEF和△AGF中,
,
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=DG+FD=BE+DF,
∴EF=BE+FD.
一.选择题(共16小题,满分32分,每小题2分)
1.在、、、、、中,分式的个数有( )
A.2个 B.3个 C.4个 D.5个
2.下列实数:15,,,﹣3π,0.10101中,无理数有( )个.
A.1 B.2 C.3 D.4
3.如图,AB,CD表示两根长度相等的铁条,若O是AB,CD的中点,经测量AC=15cm,则容器的内径长为( )
A.12cm B.13cm C.14cm D.15cm
4.若分式在实数范围内有意义,则x的取值范围是( )
A.x≠﹣5 B.x≠0 C.x≠5 D.x>﹣5
5.如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
A.∠A=∠D B.AB=DC C.∠ACB=∠DBC D.AC=BD
6.下列分式中,与的值相等的是( )
A. B. C.﹣ D.
7.一个数的两个平方根分别是2a﹣1与﹣a+2,则这个数是( )
A.﹣1 B.3 C.9 D.﹣3
8.如图,直角三角形纸片ABC中,AB=3,AC=4.D为斜边BC的中点,第1次将纸片折叠,使点A与点D重合,折痕与AD交于点P1;设P1D的中点为D1,第2次将纸片折叠,使点A与点D1重合,折痕与AD交于点P2;设P2D1的中点为D2,第3次将纸片折叠,使点A与点D2重合,折痕与AD交于点P3 ;设Pn﹣1Dn﹣2的中点为Dn﹣1,第n次将纸片折叠,使点A与点Dn﹣1重合,折痕与AD交于点Pn(n>2),则AP2019的长为( )
A. B.
C. D.
9.已知=1.147,=2.472,=0.5325,则的值是( )
A.24.72 B.53.25 C.11.47 D.114.7
10.下列各组中的两个图形属于全等图形的是( )
A. B.
C. D.
11.若分式方程有增根,则m等于( )
A.3 B.﹣3 C.2 D.﹣2
12.暑假期间,某科幻小说的销售量急剧上升.某书店分别用600元和800元两次购进该小说,第二次购进的数量比第一次多40套,且两次购书时,每套书的进价相同.若设书店第一次购进该科幻小说x套,由题意列方程正确的是( )
A. B.
C. D.
13.将数1.4960用四舍五入法取近似数,若精确到百分位,则得到的近似数是( )
A.1.49 B.1.50 C.1.496 D.1.4
14.化简+的结果是( )
A.x B.﹣x C.x﹣1 D.x+1
15.下列说法正确的是( )
A.形状相同的两个三角形全等
B.面积相等的两个三角形全等
C.完全重合的两个三角形全等
D.所有的等边三角形全等
16.如图,已知线段AB=18米,MA⊥AB于点A,MA=6米,射线BD⊥AB于B,P点从B点向A运动,每秒走1米,Q点从B点向D运动,每秒走2米,P、Q同时从B出发,则出发x秒后,在线段MA上有一点C,使△CAP与△PBQ全等,则x的值为( )
A.4 B.6 C.4或9 D.6或9
二.填空题(共4小题,满分12分,每小题3分)
17.如果一个正数a的两个不同平方根分别是2x﹣2和6﹣3x,则a= .
18.如果表示a、b的实数的点在数轴上的位置如图所示,那么化简|a﹣b|+的结果是 .
19.已知关于x的方程的解是正数,则m的取值范围为 .
20.如图,在四边形ABCD中,∠B=∠C=45°,P是BC上一点,PA=PD,∠APD=90°,= .
三.解答题(共6小题,满分56分)
21.(9分)解方程.
(1)求x的值:(x﹣3)2=16.
(2)﹣=1.
22.(9分)(1)解不等式组,并写出它的整数解.
(2)先化简,再求值:( +)÷,其中m=4.
23.(9分)比较与的大小.
24.(9分)如图,AB=AC,直线l过点A,BM⊥直线l,CN⊥直线l,垂足分别为M、N,且BM=AN.
(1)求证△AMB≌△CNA;
(2)求证∠BAC=90°.
25.(10分)某超市在2017年“双11”,销售一批用16800元购进的中老年人保暖内衣,发现供不应求.为了备战“双12”,积极参与支付宝扫码领红包活动,超市又用36400元购进了第二批这种保暖内衣,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该超市购进的第一批保暖内衣是多少件?
(2)两批保暖内衣按相同的标价销售,最后剩下的50件按六折优惠卖出,两批保暖内衣全部售完后利润没有低于进价的20%(不考虑其他因素),请计算每件保暖内衣的标价至少是多少元?
26.(10分)阅读下面材料:
小辉遇到这样一个问题:如图1,在Rt△ABC中,∠BAC=90°,AB=AC,点D,E在边BC上,∠DAE=45°.若BD=3,CE=1,求DE的长.
小辉发现,将△ABD绕点A按逆时针方向旋转90°,得到△ACF,连接EF(如图2),由图形旋转的性质和等腰直角三角形的性质以及∠DAE=45°,可证△FAE≌△DAE,得FE=DE.解△FCE,可求得FE(即DE)的长.
请回答:在图2中,∠FCE的度数是 ,DE的长为 .
参考小辉思考问题的方法,解决问题:
如图3,在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是边BC,CD上的点,且∠EAF=∠BAD.猜想线段BE,EF,FD之间的数量关系并说明理由.
参考答案与试题解析
一.选择题(共16小题,满分32分,每小题2分)
1.解:由题可得,分式有:、、,共3个.
故选:B.
2.解:15 是整数,属于有理数;
是分数,属于有理数;
0.10101是有限小数,属于有理数;
无理数有,﹣3π,共2个,
故选:B.
3.解:∵O是AB,CD的中点,AB=CD,
∴OA=OB=OD=OC,
在△AOC和△BOD中,
,
∴△AOC≌△BOD,
∴AC=BD=15cm,
故选:D.
4.解:根据分式成立的条件,可得:x+5≠0,
∴x≠﹣5,
故选:A.
5.解:A、添加∠A=∠D可利用AAS判定△ABC≌△DCB,故此选项不合题意;
B、添加AB=DC可利用SAS定理判定△ABC≌△DCB,故此选项不合题意;
C、添加∠ACB=∠DBC可利用ASA定理判定△ABC≌△DCB,故此选项不合题意;
D、添加AC=BD不能判定△ABC≌△DCB,故此选项符合题意;
故选:D.
6.解:=﹣=.
故选:D.
7.解:由题意得,
2a﹣1﹣a+2=0,
解得a=﹣1,
所以2a﹣1=﹣3,﹣a+2=3,
即一个数的两个平方根分别是3与﹣3,
所以这个数是9,
故选:C.
8.解:由题意得,AD=BC=,
AD1=AD﹣DD1=,
AD2=,
AD3=,…,
ADn=,
又∵AP1=AD1,AP2=AD2…,∴APn=ADn,
∴AP3==,APn=,
故AP2019的长为:.
故选:C.
9.解:==1.147×10=11.47.
故选:C.
10.解:A、两个图形不能完全重合,故本选项错误;
B、两个图形能够完全重合,故本选项正确;
C、两个图形不能完全重合,故本选项错误;
D、两个图形不能完全重合,故本选项错误;
故选:B.
11.解:分式方程去分母得:x﹣3=m,
由分式方程有增根,得到x﹣1=0,即x=1,
把x=1代入整式方程得:m=﹣2,
故选:D.
12.解:若设书店第一次购进该科幻小说x套,
由题意列方程正确的是,
故选:C.
13.解:1.4960≈1.50(精确到百分位),
故选:B.
14.解:原式=,
故选:A.
15.解:A、形状相同的两个三角形全等,说法错误,应该是形状相同且大小也相同的两个三角形全等;
B、面积相等的两个三角形全等,说法错误;
C、完全重合的两个三角形全等,说法正确;
D、所有的等边三角形全等,说法错误;
故选:C.
16.解:当△APC≌△BQP时,AP=BQ,即18﹣x=2x,
解得:x=6;
当△APC≌△BPQ时,AP=BP=AB=9米,
此时所用时间为9秒,AC=BQ=18米,不合题意,舍去;
综上,出发6秒后,在线段MA上有一点C,使△CAP与△PBQ全等.
故选:B.
二.填空题(共4小题,满分12分,每小题3分)
17.解:因为一个正数a的两个不同平方根分别是2x﹣2和6﹣3x,
所以2x﹣2+6﹣3x=0,
解得x=4,
于是2x﹣2=6,6﹣3x=﹣6,
即一个正数a的两个不同平方根分别是6和﹣6,
所以这个正数a的值为36,
故答案为:36.
18.解:由题意得
|a﹣b|+=a﹣b+[﹣(a+b)]
=a﹣b﹣a﹣b
=﹣2b.
故答案为:﹣2b.
19.解:分式方程去分母得:2x﹣m=x﹣1,
解得:x=m﹣1,
由分式方程的解为正数,得到m﹣1>0,且m﹣1≠1,
解得:m>1且m≠2,
故答案为:m>1且m≠2.
20.解:过点A作AE⊥BC于E,过点D作DF⊥BC于F,
由(1)可知,EF=AE+DF,
∵∠B=∠C=45°,AE⊥BC,DF⊥BC,
∴∠B=∠BAE=45°,∠C=∠CDF=45°,
∴BE=AE,CF=DF,AB=AE,CD=DF,
∴BC=BE+EF+CF=2(AE+DF),
∴==.
故答案为:.
三.解答题(共6小题,满分56分)
21.解:(1)∵(x﹣3)2=16,
∴x﹣3=4或x﹣3=﹣4,
解得x1=﹣1,x2=7;
(2)两边都乘以(x+1)(x﹣1),得:(x+1)2﹣4=(x+1)(x﹣1),
解得x=1,
经检验x=1是分式方程的增根,
∴分式方程无解.
22.解:(1),
解不等式①,得:x>﹣,
解不等式②,得:x≤2,
∴不等式组的解集为﹣<x≤2,
∴不等式组的整数解为﹣1、0、1、2;
(2)原式=
=
=,
当m=4时,原式=.
23.解:因为5>4,
所以>2,
所以﹣2>0,
所以﹣=>0,
所以>.
24.证明:(1)∵BM⊥直线l,CN⊥直线l,
∴∠AMB=∠CNA=90°,
在Rt△AMB和Rt△CNA中,
,
∴Rt△AMB≌Rt△CNA(HL);
(2)由(1)得:Rt△AMB≌Rt△CNA,
∴∠BAM=∠ACN,
∵∠CAN+∠ACN=90°,
∴∠CAN+∠BAM=90°,
∴∠BAC=180°﹣90°=90°.
25.解:(1)设该商家购进的第一批保暖内衣是x件.
根据题意,得
解方程,得x=140.
经检验,x=140是原方程的解,且符合题意.
答:该超市购进的第一批保暖内衣是140件.
(2)根据题意可知两次一共购进保暖内衣为3x=3×140=420(件).
设每件保暖内衣的标价y元.
根据题意,得
(420﹣50)y+50×0.6y≥(16800+36400)×(1+20%).
解不等式,得y≥159.6.
答:每件保暖内衣的标价至少是159.6元.
26.解:如图2,∵∠ACF=∠B=45°,
∴∠FCE=∠ACF+∠ACB=45°+45°=90°,
在Rt△EFC中,∵CF=BD=3,CE=1,
∴EF===,
∴DE=,
故答案为90°;;
如图3,
猜想:EF=BE+FD.理由如下:
如图,将△ABE绕点A按逆时针方向旋转,使AB与AD重合,得到△ADG,
∴BE=DG,AE=AG,∠DAG=∠BAE,∠B=∠ADG,
∵∠B+∠ADC=180°,
∴∠ADG+∠ADC=180°,即点F,D,G在同一条直线上,
∵∠DAG=∠BAE,
∴∠GAE=∠BAD,
∵∠EAF=∠BAD,
∴∠GAF=∠EAF,
在△AEF和△AGF中,
,
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=DG+FD=BE+DF,
∴EF=BE+FD.
同课章节目录
