2021-2022学年沪科版九年级上册数学期中复习试卷(Word版,有答案解析)
文档属性
| 名称 | 2021-2022学年沪科版九年级上册数学期中复习试卷(Word版,有答案解析) |  | |
| 格式 | zip | ||
| 文件大小 | 547.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 11:32:19 | ||
图片预览




文档简介
2021-2022学年沪科新版九年级上册数学期中复习试卷
一.选择题(共6小题,满分24分,每小题4分)
1.下面四组线段中,成比例的是( )
A.a=2,b=3,c=4,d=5 B.a=1,b=2,c=2,d=4
C.a=4,b=6,c=8,d=10 D.a=,b=,c=3,d=
2.已知在△ABC中,∠C=90°,∠B=50°,AB=10,那么BC的长为( )
A.10cos50° B.10sin50° C.10tan50° D.10cot50°
3.如图,已知△ABC∽△BDC,其中AC=4,CD=2,则BC=( )
A.2 B. C. D.4
4.下列判断错误的是( )
A.0
B.如果,,其中,那么∥
C.设为单位向量,那么
D.如果,那么或
5.如图,在正三角形ABC中,点D、E分别在AC、AB上,且,AE=BE,那么有△AED∽( )
A.△BED B.△ABD C.△CBD D.△ABC
6.如图,在△ABC中,点D、E分别在边AB、AC上,连接CD、BE交于点O,且DE∥BC,OD=1,OC=3,AD=2,则AB的长为( )
A.3 B.4 C.6 D.8
二.填空题(共12小题,满分48分,每小题4分)
7.若,则的值为 .
8.C是靠近点B的黄金分割点,若AB=10cm,则AC= cm.(结果保留根号)
9.若2||=3,那么3||= .
10.如图,在△ABC中,CA=CB=4,cosC=,则sinB的值为 .
11.太原地铁2号线是山西省第一条开通运营的地铁线路,于2020年12月26日开通,如图是该地铁某站扶梯的示意图,扶梯AB的坡度i=5:12(i为铅直高度与水平宽度的比).王老师乘扶梯从扶梯底端A以0.5米/秒的速度用时40秒到达扶梯顶端B,则王老师上升的铅直高度BC为 米.
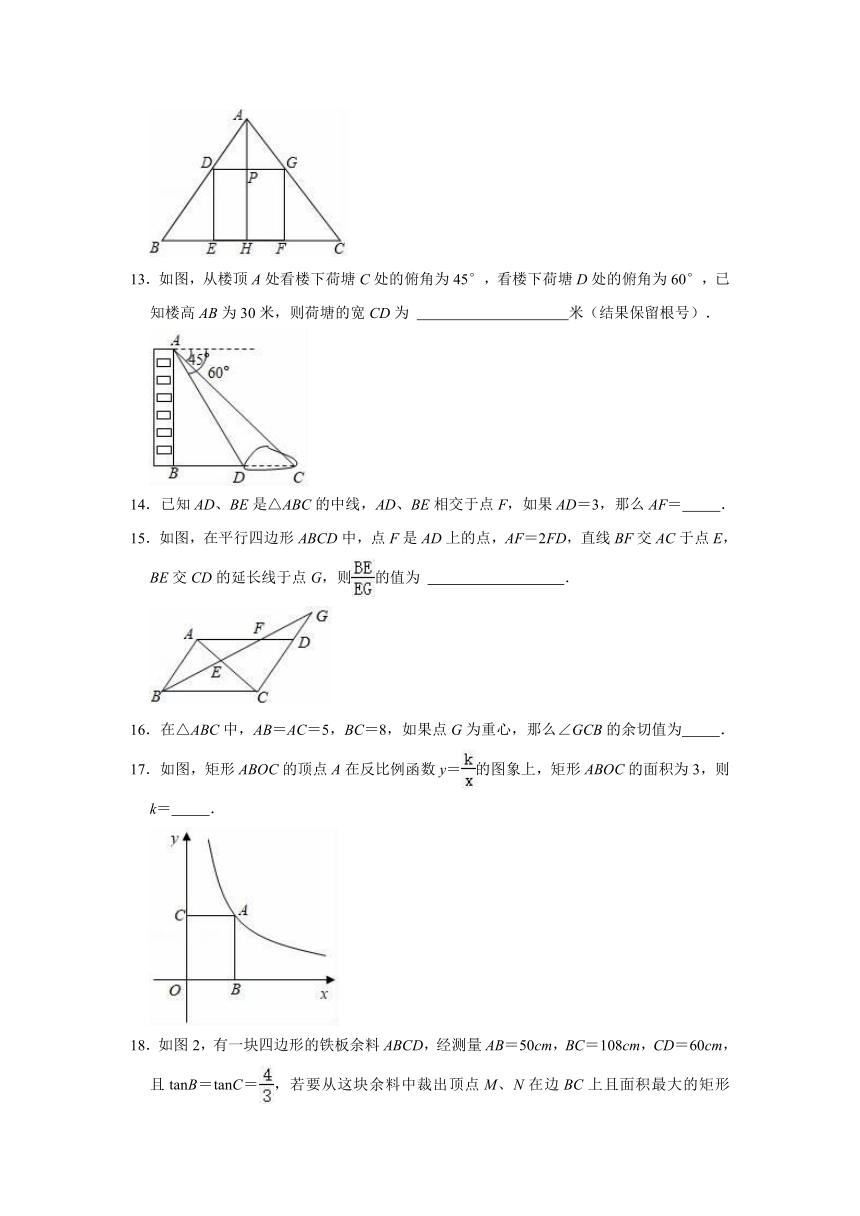
12.如图:正方形DGFE的边EF在△ABC边BC上,顶点D、G分别在边AB、AC上,AH⊥BC于H,交DG于P,已知BC=48,AH=16,那么S正方形DGEF= .
13.如图,从楼顶A处看楼下荷塘C处的俯角为45°,看楼下荷塘D处的俯角为60°,已知楼高AB为30米,则荷塘的宽CD为 米(结果保留根号).
14.已知AD、BE是△ABC的中线,AD、BE相交于点F,如果AD=3,那么AF= .
15.如图,在平行四边形ABCD中,点F是AD上的点,AF=2FD,直线BF交AC于点E,BE交CD的延长线于点G,则的值为 .
16.在△ABC中,AB=AC=5,BC=8,如果点G为重心,那么∠GCB的余切值为 .
17.如图,矩形ABOC的顶点A在反比例函数y=的图象上,矩形ABOC的面积为3,则k= .
18.如图2,有一块四边形的铁板余料ABCD,经测量AB=50cm,BC=108cm,CD=60cm,且tanB=tanC=,若要从这块余料中裁出顶点M、N在边BC上且面积最大的矩形PQMN,则该矩形的面积为 cm2.
三.解答题(共7小题,满分78分)
19.(10分)计算:2cos60°+4sin60° tan30°﹣6cos245°.
20.(10分)如图,已知点D、E分别在△ABC的边AB和AC上,DE∥BC,AD=DB,四边形DBCE的面积为16.
(1)如果向量,,请用、表示向量= .
(2)求△ABC的面积.
21.(10分)如图,在三角形ABC中,∠ACB=90°,CD⊥AB交AB于D,AD=4,BD=9,求tanA.
22.(10分)有一种落地晾衣架如图1所示,其原理是通过改变两根支撑杆夹角α的度数来调整晾杆的高度,图2是晾衣架的侧面的平面示意图,AB和CD分别是两根长度不等的支撑杆,夹角∠BOD=α,AO=70cm,BO=DO=80cm,CO=40cm.
(1)若α=56°,求点A离地面的高度AE;
(参考值:sin62°=cos28°≈0.88,sin28°=cos62°≈0.47,tan62°≈1.88,tan28°≈0.53.)
(2)调节α的大小,使A离地面高度AE=125cm时,求此时C点离地面的高度CF.
23.(12分)在梯形ABCD中,AD∥BC,∠ABC=90°,AD=CD,O为对角线AC的中点,联结BO并延长,交边DC于点E.
(1)求证:△ADC∽△BOC.
(2)若=,求的值.
(3)若CD=8,OE=3,求DE的长.
24.(12分)如图,直线y=kx+2(k<0)与x轴、y轴分别交于点B、A.
(1)如图1,点P(﹣1,3)在直线y=kx+2(k<0)上,求点A、B坐标;
(2)在(1)的条件下,如图2,点A'是点A关于x轴的对称点,点Q是第二象限内一点,连接AQ、PQ、QA'和PA',如果△PQA'和△AA'Q面积相等,且∠PAQ=∠APA',求点Q的坐标;
(3)如图3,点C和点D是该直线在第一象限内的两点,点C在点D左侧,且两点的横坐标之差为1,且CD=k+2,作CE⊥x轴,垂足为点E,连接DE,若∠OAB=2∠DEB,求k的值.
25.(14分)如图1,正方形ABCD和正方形AEFG,连接DG,BE.
(1)[发现]:当正方形AEFG绕点A旋转,如图2,线段DG与BE之间的数量关系是 ;位置关系是 ;
(2)[探究]:如图3,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE,猜想DG与BE的数量关系与位置关系,并说明理由;
(3)[应用]:在(2)情况下,连接GE(点E在AB上方),若GE∥AB,且AB=,AE=1,求线段DG的长.
参考答案与试题解析
一.选择题(共6小题,满分24分,每小题4分)
1.解:A、2×5≠3×4,故选项不符合题意;
B、1×4=2×2,故选项符合题意;
C、4×10≠6×8,故选项不符合题意;
D、×3≠×,故选项不符合题意.
故选:B.
2.解:在Rt△ABC中,
∵cosB=,∠B=50°,AB=10,
∴BC=AB cosB=10 cos50°,
故选:A.
3.解:∵△ABC∽△BDC,
∴=,
∵AC=4,CD=2,
∴BC2=AC CD=4×2=8,
∴BC=2.
故选:B.
4.解:A、0 ,故本选项不符合题意.
B、由,得到:=,=﹣,故两向量方向相反,∥,故本选项不符合题意.
C、为单位向量,那么,故本选项不符合题意.
D、由只能得到两向量模间的数量关系,不能判断其方向,判断错误,故本选项符合题意.
故选:D.
5.解:∵AD:AC=1:3,
∴AD:DC=1:2;
∵△ABC是正三角形,
∴AB=BC=AC;
∵AE=BE,
∴AE:BC=AE:AB=1:2
∴AD:DC=AE:BC;
∵∠A=∠C=60°,
∴△AED∽△CBD;
故选:C.
6.解:∵DE∥BC,
∴==,
∵DE∥BC,
∴△ADE∽△ABC,
∴==,
∴AB=3AD=6,
故选:C.
二.填空题(共12小题,满分48分,每小题4分)
7.解:∵=,
∴b=a,
∴==.
故答案为:.
8.解:由于点C是线段AB的黄金分割点,支撑点C是靠近点B的黄金分割点.
则AC=10×=5﹣5cm.
故答案为:5﹣5.
9.解:由2||=3得到:||=,
故3||=3×=.
故答案是:.
10.解:过点A作AD⊥BC,垂足为D,如图所示.
在Rt△ACD中,CD=CA cosC=4×=1,
∴AD===;
在Rt△ABD中,BD=CB﹣CD=4﹣1=3,AD=,
∴AB===2,
∴sinB===.
故答案为:.
11.解:由题意得:∠ACB=90°,AB=0.5×40=20(米),
∵扶梯AB的坡度i=5:12=,
∴设BC=5a米,则AC=12a米,
由勾股定理得:(5a)2+(12a)2=202,
解得:a=(负值已舍去),
∴BC=(米),
故答案为:.
12.解:设正方形DGEF的边长为x.
由正方形DEFG得,DG∥EF,即DG∥BC,
∵AH⊥BC,
∴AP⊥DG.
∵DG∥BC,
∴△ADG∽△ABC,
∴.
∵PH⊥BC,DE⊥BC,
∴PH=ED,AP=AH﹣PH,
即.
由BC=48,AH=16,DE=DG=x,
得,
解得x=12.
∴正方形DEFG的边长是12,
∴S正方形DGEF=DE2=122=144.
故答案为144.
13.解:由题意可得,∠ADB=60°,∠ACB=45°,AB=30m,
在Rt△ABC中,
∵∠ACB=45°,
∴AB=BC,
在Rt△ABD中,
∵∠ADB=60°,
∴BD=AB=10(m),
∴CD=BC﹣BD=(30﹣10)m,
故答案为:(30﹣10).
14.解:连接DE,
∵AD、BE是△ABC的中线,
∴DE是△ABC的中位线,
∴DE=AB,DE∥AB,
∴△AFB∽△DFE,
∴==2,
∴AF=2FD,
∵AD=3,
∴AF=2,
故答案为:2.
15.解:由AF=2DF,可以假设DF=k,则AF=2k,AD=3k,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AD=BC=3k,
∴==,
∴==,
故答案为:.
16.解:作AD⊥BC于D,
则点G在AD上,连接GC,
∵AB=AC,AD⊥BC,
∴CD=BC=4,
由勾股定理得,AD==3,
∵G为△ABC的重心,
∴DG=AD=1,
∴cot∠GCB==4,
故答案为:4.
17.解:∵矩形ABOC的面积为3,
∴|k|=3,
又∵k>0,
∴k=3,
故答案为:3.
18.解:如图,延长BA、CD交于点E,过点E作EH⊥BC于点H,
交PQ于点G,如图,设矩形PQMN,
∵tanB=tanC=,
∴∠B=∠C,
∴EB=EC,
∵BC=108cm,且EH⊥BC,
∴BH=CH=BC=54cm,
∵tanB==,
∴EH=BH=×54=72cm,
∴EG=EH﹣GH=72﹣QM,
∵PQ∥BC,
∴△EQP∽△EBC,
∴=,即=,
∴PQ=(72﹣QM),
设QM=x,
则S矩形PQMN=PQ QM=x(72﹣x)=﹣(x﹣36)2+1944,
∴当x=36时,S矩形PQMN最大值为1944,
所以当QM=36时,矩形PQMN的最大面积为1944cm2,
答:该矩形的面积为1944cm2.
故答案为:1944.
三.解答题(共7小题,满分78分)
19.解:原式=2×+4××﹣6×()2
=1+2﹣3
=0.
20.解:(1)∵,,
∴=,
∵DE∥BC,AD=DB,
∴,
∴
=
=,
故答案为:;
(2)由(1)知,,
∴,
∴S△ABC:S四边形DECB=9:8,
∵S四边形DECB=16,
∴S△ABC=18.
21.解:∵∠ACB=90°,CD⊥AB,
∴∠B+∠A=∠A+∠ACD=∠B+∠BCD=90°,
∴△BCD∽△ACD,
∴CD2=AD BD=36,
∴CD=6,
∴tanA===.
22.解:(1)如图,过O作OG⊥BD于点G,
∵AE⊥BD,
∴OG∥AE,
∵BO=DO,
∴OG平分∠BOD,
∴∠BOG=∠BOD=×56°=28°,
∴∠EAB=∠BOG=28°,
在Rt△ABE中,AB=AO+BO=70+80=150(cm),
∴AE=AB cos∠EAB=150×cos28°≈150×0.88=132(cm),
答:点A离地面的高度AE约为132cm;
(2)∵OG∥AE,
∴∠EAB=∠BOG,
∵CF⊥BD,
∴CF∥OG,
∴∠DCF=∠DOG,
∵∠BOG=∠DOG,
∴∠BAE=∠DCF,
∵∠AEB=∠CFD=90°,
∴△AEB∽△CFD,
∴=,
∴CF===100(cm),
答:C点离地面的高度CF为100cm.
23.(1)证明:∵∠ABC=90°,O为对角线AC的中点,
∴BO=CO=AO,
∴∠OBC=∠OCB,
∵AD=CD,
∴∠DAC=∠DCA,
∵AD∥BC,
∴∠DAC=∠ACB,
∴∠DAC=∠DCA=∠ACB=∠OBC,
∴△ADC∽△BOC;
(2)如图,延长AD,BE交于点F,
∵AD∥BC,
∴△AOF∽△COB,△DEF∽△CEB,
∴=1=,,
∴BO=OF,AF=BC,BE=3EF,
∴BF=4EF,
∴BO=OF=2EF,
∴EO=OF﹣EF=EF,
∴;
(3)设BO=AO=CO=x=OF,
∴AC=2x,
∵CD=8,OE=3,
∴AD=CD=8,EF=x﹣3,BE=x+3,
∵△ADC∽△BOC,
∴,
∴,
∴BC==AF,
∴DF=﹣8,
∵△DEF∽△CEB,
∴,
∴=,
∴x=(负值舍去),
∴===,
∴DE=8×=6﹣.
24.解:(1)当x=0时,y=2,
∴A(0,2),
把点P(﹣1,3)代入直线y=kx+2(k<0)得:﹣k+2=3,
解得:k=﹣1,
∴直线AB的解析式为y=﹣x+2,
当y=0时,﹣x+2=0,
解得:x=2,
∴B(2,0);
(2)分两种情况:
①点Q在直线AB的下方时,过点A'作A'Q∥AB,设AQ与A'P交点为M,延长QP交y轴于点N,如图2所示:
∵平行线间的距离处处相等,且QA'为公共底边,
∴△PQA'和△AA'Q面积相等,
∵∠PAQ=∠APA',
∴MA=MP,
∵A'Q∥AB,
∴∠PAQ=∠AQA',∠APA'=∠PA'Q,
∴∠AQA'=∠PA'Q,
∴A'M=QM,
∴AQ=A'P,
∴△PQA'≌△AA'Q(SAS),
∴∠PQA'=∠AA'Q,PQ=AA',
∵点A'是点A关于x轴的对称点,A(0,2),
∴A'(0,﹣2),
∴PQ=AA'=2+2=4,
由(1)可知OA=OB,
∴∠BAO=45°,
∵A'Q∥AP,
∴∠PQA'=∠AA'Q=45°,
∴∠QNO=90°,
∴QN⊥y轴,
∵P(﹣1,3),
∴PN=1,ON=3,
∴QN=PQ+PN=5,
∴Q(﹣5,3);
②当点Q在直线AB的上方时,如图2﹣1所示:
∵∠PAQ=∠APA',
∴AQ∥A'P,
当PQ∥AA'时,四边形A'PQA是平行四边形,
∴△PQA'的面积=△AA'Q面积,
此时Q(﹣1,7),满足条件;
综上所述,点Q的坐标为(﹣5,3)或(﹣1,7);
(3)过D作DF⊥CE于F,如图3所示:
∵∠CEB=90°,
∴∠CED=90°﹣∠DEB,
∵CE∥OA,
∴∠OAB=∠ECD,
∵∠OAB=2∠DEB,
∴∠ECD=2∠DEB,
∴∠CDE=180°﹣∠ECD﹣∠CED=180°﹣2∠DEB﹣(90°﹣∠DEB)=90°﹣∠DEB,
∴∠CDE=∠CED,
∴CE=CD=k+2,
∵点C在直线y=kx+2上,
∴当y=k+2时,有k+2=kx+2,
∴x=1,
∴点C(1,k+2),D(2,2k+2),
∴DF=1,CF=﹣k,CE=k+2,
在Rt△CDF中,由勾股定理得:CF2+DF2=CD2,
∴CF2+DF2=CE2,
即(﹣k)2+12=(k+2)2,
解得:k=﹣.
25.解:(1)DG=BE,DG⊥BE,理由如下:
∵四边形ABCD和四边形AEFG是正方形,
∴AE=AG,AB=AD,∠BAD=∠EAG=90°,
∴∠BAE=∠DAG,
∴△ABE≌△ADG(SAS),
∴BE=DG;
如图2,延长BE交AD于Q,交DG于H,
∵△ABE≌△DAG,
∴∠ABE=∠ADG,
∵∠AQB+∠ABE=90°,
∴∠AQB+∠ADG=90°,
∵∠AQB=∠DQH,
∴∠DQH+∠ADG=90°,
∴∠DHB=90°,
∴BE⊥DG,
故答案为:DG=BE,DG⊥BE;
(2)DG=2BE,BE⊥DG,理由如下:
如图3,延长BE交AD于K,交DG于H,
∵四边形ABCD与四边形AEFG都为矩形,
∴∠BAD=∠EAG,
∴∠BAE=∠DAG,
∵AD=2AB,AG=2AE,
∴==,
∴△ABE∽△ADG,
∴==,∠ABE=∠ADG,
∴DG=2BE,
∵∠AKB+∠ABE=90°,
∴∠AKB+∠ADG=90°,
∵∠AKB=∠DKH,
∴∠DKH+∠ADG=90°,
∴∠DHB=90°,
∴BE⊥DG;
(3)如图4,(为了说明点B,E,F在同一条线上,特意画的图形)
设EG与AD的交点为M,
∵EG∥AB,
∴∠DME=∠DAB=90°,
在Rt△AEG中,AE=1,
∴AG=2AE=2,
根据勾股定理得:EG==,
∵AB=,
∴EG=AB,
∵EG∥AB,
∴四边形ABEG是平行四边形,
∴AG∥BE,
∵AG∥EF,
∴点B,E,F在同一条直线上,如图5,
∴∠AEB=90°,
在Rt△ABE中,根据勾股定理得,BE===2,
由(2)知,△ABE∽△ADG,
∴==,
即=,
∴DG=4.
一.选择题(共6小题,满分24分,每小题4分)
1.下面四组线段中,成比例的是( )
A.a=2,b=3,c=4,d=5 B.a=1,b=2,c=2,d=4
C.a=4,b=6,c=8,d=10 D.a=,b=,c=3,d=
2.已知在△ABC中,∠C=90°,∠B=50°,AB=10,那么BC的长为( )
A.10cos50° B.10sin50° C.10tan50° D.10cot50°
3.如图,已知△ABC∽△BDC,其中AC=4,CD=2,则BC=( )
A.2 B. C. D.4
4.下列判断错误的是( )
A.0
B.如果,,其中,那么∥
C.设为单位向量,那么
D.如果,那么或
5.如图,在正三角形ABC中,点D、E分别在AC、AB上,且,AE=BE,那么有△AED∽( )
A.△BED B.△ABD C.△CBD D.△ABC
6.如图,在△ABC中,点D、E分别在边AB、AC上,连接CD、BE交于点O,且DE∥BC,OD=1,OC=3,AD=2,则AB的长为( )
A.3 B.4 C.6 D.8
二.填空题(共12小题,满分48分,每小题4分)
7.若,则的值为 .
8.C是靠近点B的黄金分割点,若AB=10cm,则AC= cm.(结果保留根号)
9.若2||=3,那么3||= .
10.如图,在△ABC中,CA=CB=4,cosC=,则sinB的值为 .
11.太原地铁2号线是山西省第一条开通运营的地铁线路,于2020年12月26日开通,如图是该地铁某站扶梯的示意图,扶梯AB的坡度i=5:12(i为铅直高度与水平宽度的比).王老师乘扶梯从扶梯底端A以0.5米/秒的速度用时40秒到达扶梯顶端B,则王老师上升的铅直高度BC为 米.
12.如图:正方形DGFE的边EF在△ABC边BC上,顶点D、G分别在边AB、AC上,AH⊥BC于H,交DG于P,已知BC=48,AH=16,那么S正方形DGEF= .
13.如图,从楼顶A处看楼下荷塘C处的俯角为45°,看楼下荷塘D处的俯角为60°,已知楼高AB为30米,则荷塘的宽CD为 米(结果保留根号).
14.已知AD、BE是△ABC的中线,AD、BE相交于点F,如果AD=3,那么AF= .
15.如图,在平行四边形ABCD中,点F是AD上的点,AF=2FD,直线BF交AC于点E,BE交CD的延长线于点G,则的值为 .
16.在△ABC中,AB=AC=5,BC=8,如果点G为重心,那么∠GCB的余切值为 .
17.如图,矩形ABOC的顶点A在反比例函数y=的图象上,矩形ABOC的面积为3,则k= .
18.如图2,有一块四边形的铁板余料ABCD,经测量AB=50cm,BC=108cm,CD=60cm,且tanB=tanC=,若要从这块余料中裁出顶点M、N在边BC上且面积最大的矩形PQMN,则该矩形的面积为 cm2.
三.解答题(共7小题,满分78分)
19.(10分)计算:2cos60°+4sin60° tan30°﹣6cos245°.
20.(10分)如图,已知点D、E分别在△ABC的边AB和AC上,DE∥BC,AD=DB,四边形DBCE的面积为16.
(1)如果向量,,请用、表示向量= .
(2)求△ABC的面积.
21.(10分)如图,在三角形ABC中,∠ACB=90°,CD⊥AB交AB于D,AD=4,BD=9,求tanA.
22.(10分)有一种落地晾衣架如图1所示,其原理是通过改变两根支撑杆夹角α的度数来调整晾杆的高度,图2是晾衣架的侧面的平面示意图,AB和CD分别是两根长度不等的支撑杆,夹角∠BOD=α,AO=70cm,BO=DO=80cm,CO=40cm.
(1)若α=56°,求点A离地面的高度AE;
(参考值:sin62°=cos28°≈0.88,sin28°=cos62°≈0.47,tan62°≈1.88,tan28°≈0.53.)
(2)调节α的大小,使A离地面高度AE=125cm时,求此时C点离地面的高度CF.
23.(12分)在梯形ABCD中,AD∥BC,∠ABC=90°,AD=CD,O为对角线AC的中点,联结BO并延长,交边DC于点E.
(1)求证:△ADC∽△BOC.
(2)若=,求的值.
(3)若CD=8,OE=3,求DE的长.
24.(12分)如图,直线y=kx+2(k<0)与x轴、y轴分别交于点B、A.
(1)如图1,点P(﹣1,3)在直线y=kx+2(k<0)上,求点A、B坐标;
(2)在(1)的条件下,如图2,点A'是点A关于x轴的对称点,点Q是第二象限内一点,连接AQ、PQ、QA'和PA',如果△PQA'和△AA'Q面积相等,且∠PAQ=∠APA',求点Q的坐标;
(3)如图3,点C和点D是该直线在第一象限内的两点,点C在点D左侧,且两点的横坐标之差为1,且CD=k+2,作CE⊥x轴,垂足为点E,连接DE,若∠OAB=2∠DEB,求k的值.
25.(14分)如图1,正方形ABCD和正方形AEFG,连接DG,BE.
(1)[发现]:当正方形AEFG绕点A旋转,如图2,线段DG与BE之间的数量关系是 ;位置关系是 ;
(2)[探究]:如图3,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE,猜想DG与BE的数量关系与位置关系,并说明理由;
(3)[应用]:在(2)情况下,连接GE(点E在AB上方),若GE∥AB,且AB=,AE=1,求线段DG的长.
参考答案与试题解析
一.选择题(共6小题,满分24分,每小题4分)
1.解:A、2×5≠3×4,故选项不符合题意;
B、1×4=2×2,故选项符合题意;
C、4×10≠6×8,故选项不符合题意;
D、×3≠×,故选项不符合题意.
故选:B.
2.解:在Rt△ABC中,
∵cosB=,∠B=50°,AB=10,
∴BC=AB cosB=10 cos50°,
故选:A.
3.解:∵△ABC∽△BDC,
∴=,
∵AC=4,CD=2,
∴BC2=AC CD=4×2=8,
∴BC=2.
故选:B.
4.解:A、0 ,故本选项不符合题意.
B、由,得到:=,=﹣,故两向量方向相反,∥,故本选项不符合题意.
C、为单位向量,那么,故本选项不符合题意.
D、由只能得到两向量模间的数量关系,不能判断其方向,判断错误,故本选项符合题意.
故选:D.
5.解:∵AD:AC=1:3,
∴AD:DC=1:2;
∵△ABC是正三角形,
∴AB=BC=AC;
∵AE=BE,
∴AE:BC=AE:AB=1:2
∴AD:DC=AE:BC;
∵∠A=∠C=60°,
∴△AED∽△CBD;
故选:C.
6.解:∵DE∥BC,
∴==,
∵DE∥BC,
∴△ADE∽△ABC,
∴==,
∴AB=3AD=6,
故选:C.
二.填空题(共12小题,满分48分,每小题4分)
7.解:∵=,
∴b=a,
∴==.
故答案为:.
8.解:由于点C是线段AB的黄金分割点,支撑点C是靠近点B的黄金分割点.
则AC=10×=5﹣5cm.
故答案为:5﹣5.
9.解:由2||=3得到:||=,
故3||=3×=.
故答案是:.
10.解:过点A作AD⊥BC,垂足为D,如图所示.
在Rt△ACD中,CD=CA cosC=4×=1,
∴AD===;
在Rt△ABD中,BD=CB﹣CD=4﹣1=3,AD=,
∴AB===2,
∴sinB===.
故答案为:.
11.解:由题意得:∠ACB=90°,AB=0.5×40=20(米),
∵扶梯AB的坡度i=5:12=,
∴设BC=5a米,则AC=12a米,
由勾股定理得:(5a)2+(12a)2=202,
解得:a=(负值已舍去),
∴BC=(米),
故答案为:.
12.解:设正方形DGEF的边长为x.
由正方形DEFG得,DG∥EF,即DG∥BC,
∵AH⊥BC,
∴AP⊥DG.
∵DG∥BC,
∴△ADG∽△ABC,
∴.
∵PH⊥BC,DE⊥BC,
∴PH=ED,AP=AH﹣PH,
即.
由BC=48,AH=16,DE=DG=x,
得,
解得x=12.
∴正方形DEFG的边长是12,
∴S正方形DGEF=DE2=122=144.
故答案为144.
13.解:由题意可得,∠ADB=60°,∠ACB=45°,AB=30m,
在Rt△ABC中,
∵∠ACB=45°,
∴AB=BC,
在Rt△ABD中,
∵∠ADB=60°,
∴BD=AB=10(m),
∴CD=BC﹣BD=(30﹣10)m,
故答案为:(30﹣10).
14.解:连接DE,
∵AD、BE是△ABC的中线,
∴DE是△ABC的中位线,
∴DE=AB,DE∥AB,
∴△AFB∽△DFE,
∴==2,
∴AF=2FD,
∵AD=3,
∴AF=2,
故答案为:2.
15.解:由AF=2DF,可以假设DF=k,则AF=2k,AD=3k,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AD=BC=3k,
∴==,
∴==,
故答案为:.
16.解:作AD⊥BC于D,
则点G在AD上,连接GC,
∵AB=AC,AD⊥BC,
∴CD=BC=4,
由勾股定理得,AD==3,
∵G为△ABC的重心,
∴DG=AD=1,
∴cot∠GCB==4,
故答案为:4.
17.解:∵矩形ABOC的面积为3,
∴|k|=3,
又∵k>0,
∴k=3,
故答案为:3.
18.解:如图,延长BA、CD交于点E,过点E作EH⊥BC于点H,
交PQ于点G,如图,设矩形PQMN,
∵tanB=tanC=,
∴∠B=∠C,
∴EB=EC,
∵BC=108cm,且EH⊥BC,
∴BH=CH=BC=54cm,
∵tanB==,
∴EH=BH=×54=72cm,
∴EG=EH﹣GH=72﹣QM,
∵PQ∥BC,
∴△EQP∽△EBC,
∴=,即=,
∴PQ=(72﹣QM),
设QM=x,
则S矩形PQMN=PQ QM=x(72﹣x)=﹣(x﹣36)2+1944,
∴当x=36时,S矩形PQMN最大值为1944,
所以当QM=36时,矩形PQMN的最大面积为1944cm2,
答:该矩形的面积为1944cm2.
故答案为:1944.
三.解答题(共7小题,满分78分)
19.解:原式=2×+4××﹣6×()2
=1+2﹣3
=0.
20.解:(1)∵,,
∴=,
∵DE∥BC,AD=DB,
∴,
∴
=
=,
故答案为:;
(2)由(1)知,,
∴,
∴S△ABC:S四边形DECB=9:8,
∵S四边形DECB=16,
∴S△ABC=18.
21.解:∵∠ACB=90°,CD⊥AB,
∴∠B+∠A=∠A+∠ACD=∠B+∠BCD=90°,
∴△BCD∽△ACD,
∴CD2=AD BD=36,
∴CD=6,
∴tanA===.
22.解:(1)如图,过O作OG⊥BD于点G,
∵AE⊥BD,
∴OG∥AE,
∵BO=DO,
∴OG平分∠BOD,
∴∠BOG=∠BOD=×56°=28°,
∴∠EAB=∠BOG=28°,
在Rt△ABE中,AB=AO+BO=70+80=150(cm),
∴AE=AB cos∠EAB=150×cos28°≈150×0.88=132(cm),
答:点A离地面的高度AE约为132cm;
(2)∵OG∥AE,
∴∠EAB=∠BOG,
∵CF⊥BD,
∴CF∥OG,
∴∠DCF=∠DOG,
∵∠BOG=∠DOG,
∴∠BAE=∠DCF,
∵∠AEB=∠CFD=90°,
∴△AEB∽△CFD,
∴=,
∴CF===100(cm),
答:C点离地面的高度CF为100cm.
23.(1)证明:∵∠ABC=90°,O为对角线AC的中点,
∴BO=CO=AO,
∴∠OBC=∠OCB,
∵AD=CD,
∴∠DAC=∠DCA,
∵AD∥BC,
∴∠DAC=∠ACB,
∴∠DAC=∠DCA=∠ACB=∠OBC,
∴△ADC∽△BOC;
(2)如图,延长AD,BE交于点F,
∵AD∥BC,
∴△AOF∽△COB,△DEF∽△CEB,
∴=1=,,
∴BO=OF,AF=BC,BE=3EF,
∴BF=4EF,
∴BO=OF=2EF,
∴EO=OF﹣EF=EF,
∴;
(3)设BO=AO=CO=x=OF,
∴AC=2x,
∵CD=8,OE=3,
∴AD=CD=8,EF=x﹣3,BE=x+3,
∵△ADC∽△BOC,
∴,
∴,
∴BC==AF,
∴DF=﹣8,
∵△DEF∽△CEB,
∴,
∴=,
∴x=(负值舍去),
∴===,
∴DE=8×=6﹣.
24.解:(1)当x=0时,y=2,
∴A(0,2),
把点P(﹣1,3)代入直线y=kx+2(k<0)得:﹣k+2=3,
解得:k=﹣1,
∴直线AB的解析式为y=﹣x+2,
当y=0时,﹣x+2=0,
解得:x=2,
∴B(2,0);
(2)分两种情况:
①点Q在直线AB的下方时,过点A'作A'Q∥AB,设AQ与A'P交点为M,延长QP交y轴于点N,如图2所示:
∵平行线间的距离处处相等,且QA'为公共底边,
∴△PQA'和△AA'Q面积相等,
∵∠PAQ=∠APA',
∴MA=MP,
∵A'Q∥AB,
∴∠PAQ=∠AQA',∠APA'=∠PA'Q,
∴∠AQA'=∠PA'Q,
∴A'M=QM,
∴AQ=A'P,
∴△PQA'≌△AA'Q(SAS),
∴∠PQA'=∠AA'Q,PQ=AA',
∵点A'是点A关于x轴的对称点,A(0,2),
∴A'(0,﹣2),
∴PQ=AA'=2+2=4,
由(1)可知OA=OB,
∴∠BAO=45°,
∵A'Q∥AP,
∴∠PQA'=∠AA'Q=45°,
∴∠QNO=90°,
∴QN⊥y轴,
∵P(﹣1,3),
∴PN=1,ON=3,
∴QN=PQ+PN=5,
∴Q(﹣5,3);
②当点Q在直线AB的上方时,如图2﹣1所示:
∵∠PAQ=∠APA',
∴AQ∥A'P,
当PQ∥AA'时,四边形A'PQA是平行四边形,
∴△PQA'的面积=△AA'Q面积,
此时Q(﹣1,7),满足条件;
综上所述,点Q的坐标为(﹣5,3)或(﹣1,7);
(3)过D作DF⊥CE于F,如图3所示:
∵∠CEB=90°,
∴∠CED=90°﹣∠DEB,
∵CE∥OA,
∴∠OAB=∠ECD,
∵∠OAB=2∠DEB,
∴∠ECD=2∠DEB,
∴∠CDE=180°﹣∠ECD﹣∠CED=180°﹣2∠DEB﹣(90°﹣∠DEB)=90°﹣∠DEB,
∴∠CDE=∠CED,
∴CE=CD=k+2,
∵点C在直线y=kx+2上,
∴当y=k+2时,有k+2=kx+2,
∴x=1,
∴点C(1,k+2),D(2,2k+2),
∴DF=1,CF=﹣k,CE=k+2,
在Rt△CDF中,由勾股定理得:CF2+DF2=CD2,
∴CF2+DF2=CE2,
即(﹣k)2+12=(k+2)2,
解得:k=﹣.
25.解:(1)DG=BE,DG⊥BE,理由如下:
∵四边形ABCD和四边形AEFG是正方形,
∴AE=AG,AB=AD,∠BAD=∠EAG=90°,
∴∠BAE=∠DAG,
∴△ABE≌△ADG(SAS),
∴BE=DG;
如图2,延长BE交AD于Q,交DG于H,
∵△ABE≌△DAG,
∴∠ABE=∠ADG,
∵∠AQB+∠ABE=90°,
∴∠AQB+∠ADG=90°,
∵∠AQB=∠DQH,
∴∠DQH+∠ADG=90°,
∴∠DHB=90°,
∴BE⊥DG,
故答案为:DG=BE,DG⊥BE;
(2)DG=2BE,BE⊥DG,理由如下:
如图3,延长BE交AD于K,交DG于H,
∵四边形ABCD与四边形AEFG都为矩形,
∴∠BAD=∠EAG,
∴∠BAE=∠DAG,
∵AD=2AB,AG=2AE,
∴==,
∴△ABE∽△ADG,
∴==,∠ABE=∠ADG,
∴DG=2BE,
∵∠AKB+∠ABE=90°,
∴∠AKB+∠ADG=90°,
∵∠AKB=∠DKH,
∴∠DKH+∠ADG=90°,
∴∠DHB=90°,
∴BE⊥DG;
(3)如图4,(为了说明点B,E,F在同一条线上,特意画的图形)
设EG与AD的交点为M,
∵EG∥AB,
∴∠DME=∠DAB=90°,
在Rt△AEG中,AE=1,
∴AG=2AE=2,
根据勾股定理得:EG==,
∵AB=,
∴EG=AB,
∵EG∥AB,
∴四边形ABEG是平行四边形,
∴AG∥BE,
∵AG∥EF,
∴点B,E,F在同一条直线上,如图5,
∴∠AEB=90°,
在Rt△ABE中,根据勾股定理得,BE===2,
由(2)知,△ABE∽△ADG,
∴==,
即=,
∴DG=4.
同课章节目录
