2021-2022学年河北省唐山市迁安市七年级(上)期中数学试卷(Word版 含解析)
文档属性
| 名称 | 2021-2022学年河北省唐山市迁安市七年级(上)期中数学试卷(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 619.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 00:00:00 | ||
图片预览




文档简介
2021-2022学年河北省唐山市迁安市七年级第一学期期中数学试卷
一、选择题:(本大题有16个小题,每小题2分,共32分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.如果将向东行驶3km记作+3km,那么向西行驶2km应记作( )
A.+2km B.﹣2km C.+3km D.﹣3km
2.﹣是一个数的相反数,这个数是( )
A.2 B.﹣2 C. D.﹣
3.若|a+2|+|b﹣7|=0,则a+b的值为( )
A.﹣1 B.1 C.5 D.﹣5
4.根据直线、射线、线段的性质,图中的各组直线、射线、线段一定能相交的是( )
A. B.
C. D.
5.下列说法正确的是( )
A.角的大小和开口的大小无关
B.互余、互补是指两个角之间的数量关系
C.单独的一个角也可以叫余角或补角
D.若三个角的和是直角,则他们互余
6.如图,已知直线AB、CD相交于点O,OA平分∠EOC,∠EOC=110°,则∠BOD的度数是( )
A.25° B.35° C.45° D.55°
7.如图,若A是实数a在数轴上对应的点,则关于a,﹣a,1的大小关系表示正确的是( )
A.a<1<﹣a B.a<﹣a<1 C.1<﹣a<a D.﹣a<a<1
8.在直线l上顺次取A、B、C三点,使得AB=5cm,BC=3cm,如果O是线段AC的中点,那么线段OB的长度是( )
A.0.5 cm B.1 cm C.1.5 cm D.2 cm
9.下面等式成立的是( )
A.83.5°=83°50′ B.37°12′36″=37.48°
C.24°24′24″=24.44° D.41.25°=41°15′
10.当分针指向12,时针这时恰好与分针成30°的角,此时是( )
A.9点钟 B.10点钟
C.11点钟或1点钟 D.2点钟或10点钟
11.小明做了以下4道计算题:①(﹣1)2020+(﹣2)=﹣3;②0﹣(﹣1)=1;③﹣×=﹣;④÷(﹣)=﹣1.请你帮他检查一下,他一共做对了( )
A.4题 B.3题 C.2题 D.1题
12.如图,将△ABC就点C按逆时针方向旋转75°后得到△A′B′C,若∠ACB=25°,则∠BCA′的度数为( )
A.50° B.40° C.25° D.60°
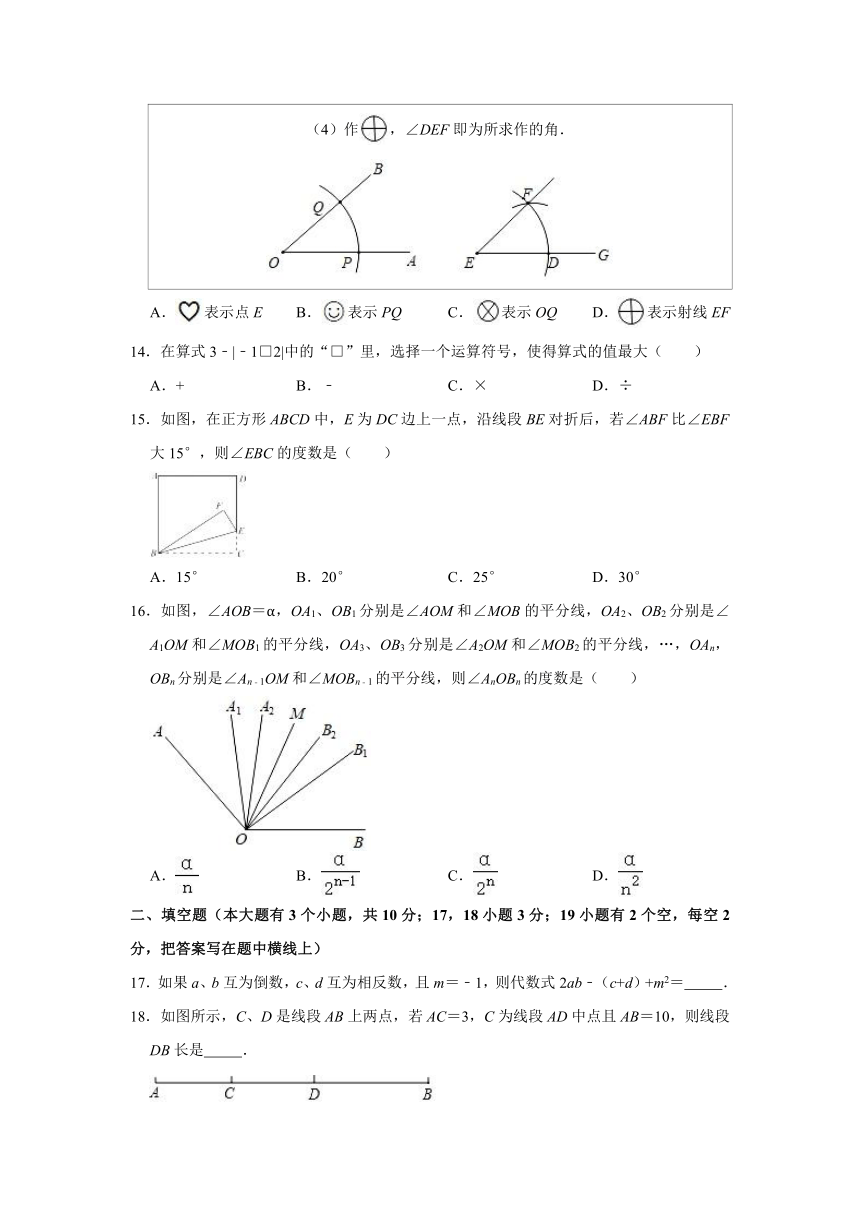
13.下面是黑板上出示的尺规作图题,需要回答符号代表的内容( )
如图,已知∠AOB,求作:∠DEF,使∠DEF=∠AOB作法:(1)以为圆心,任意长为半径画弧,分别交OA、OB于点P、Q;(2)作射线EG,并以点E为圆心长为半径画弧交EG于点D;(3)以点D为圆心长为半径画弧交(2)步中所画弧于点F;(4)作,∠DEF即为所求作的角.
A.表示点E B.表示PQ C.表示OQ D.表示射线EF
14.在算式3﹣|﹣1□2|中的“□”里,选择一个运算符号,使得算式的值最大( )
A.+ B.﹣ C.× D.÷
15.如图,在正方形ABCD中,E为DC边上一点,沿线段BE对折后,若∠ABF比∠EBF大15°,则∠EBC的度数是( )
A.15° B.20° C.25° D.30°
16.如图,∠AOB=α,OA1、OB1分别是∠AOM和∠MOB的平分线,OA2、OB2分别是∠A1OM和∠MOB1的平分线,OA3、OB3分别是∠A2OM和∠MOB2的平分线,…,OAn,OBn分别是∠An﹣1OM和∠MOBn﹣1的平分线,则∠AnOBn的度数是( )
A. B. C. D.
二、填空题(本大题有3个小题,共10分;17,18小题3分;19小题有2个空,每空2分,把答案写在题中横线上)
17.如果a、b互为倒数,c、d互为相反数,且m=﹣1,则代数式2ab﹣(c+d)+m2= .
18.如图所示,C、D是线段AB上两点,若AC=3,C为线段AD中点且AB=10,则线段DB长是 .
19.数学家发明了一个魔术盒,当任意数对(a,b)放入其中时,会得到一个新的数:a2+b+1.例如把(3,﹣2)放入其中,就会得到32+(﹣2)+1=8.现将数对(﹣2,3)放入其中得到数m= ,再将数对(m,1)放入其中后,得到的数是 .
三、解答题(本大题有6个小题,共5分,解答应写出文字说明、证明过程或演算步骤)
20.(1)计算:11﹣18﹣12+19.
(2)计算:﹣12+2014×(﹣)3×0﹣(﹣3).
21.计算:
(1);
(2).
22.如图,已知线段AB,按下列要求完成画图和计算:
(1)延长线段AB到点C,使BC=3AB(尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,如果点D为线段BC的中点,且AB=2,求线段AD的长度;
(3)在以上的条件下,若点P从A点出发,以每秒1个单位长度的速度向点C移动,到点C时停止.设点P的运动时间为t秒,是否存在某时刻t,使得PB=PA﹣PC?若存在,求出时间t:若不存在,请说明理由.
23.某检修小组从A地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶记录如下.(单位:千米)
第一次 第二次 第三次 第四次 第五次 第六次 第七次
﹣4 +7 ﹣9 +8 +6 ﹣5 ﹣2
(1)求收工时距A地多远?
(2)在第几次记录时距A地最远?距离A多远?
(3)若每千米耗油0.3升,问共耗油多少升?
24.如图所示,观察数轴,请回答:
(1)点C与点D的距离为 ,点B与点D的距离为 ;
点B与点E的距离为 ,点C与点A的距离为 ;
(2)发现:在数轴上,如果点M与点N分别表示数m,n,则它们之间的距离可表示为MN= (用m,n表示);
(3)利用发现的结论,逆向思维解决下列问题:
①数轴上表示x的点P与B之间的距离是1,则x的值是 ;
②|x+3|=2,则x= ;
③数轴上是否存在表示x的点P,使点P到点B、点C的距离之和为11?若存在,请求出x的值;若不存在,说明理由;
④|x+2|+|x﹣7|的最小值为 ;
25.已知,如图1,把直角三角形MON的直角顶点O放在直线AB上,射线OC平分∠AON.
(1)如图1,若∠MOC=28°,求∠BON的度数;
(2)若将三角形MON绕点O旋转到如图2所示的位置,若∠BON=100°,则∠MOC的度数为 ;
(3)若将三角形MON绕点O旋转到如图3所示的位置,试写出∠BON和∠MOC之间的数量关系,并说明理由.
参考答案
一、选择题:(本大题有16个小题,每小题2分,共32分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.如果将向东行驶3km记作+3km,那么向西行驶2km应记作( )
A.+2km B.﹣2km C.+3km D.﹣3km
【分析】根据正数和负数表示相反意义的量,向东记为正,可得答案.
解:向东行驶3km,记作+3km,向西行驶2km记作﹣2km,
故选:B.
2.﹣是一个数的相反数,这个数是( )
A.2 B.﹣2 C. D.﹣
【分析】根据相反数的概念:只有符号不同的两个数叫做互为相反数,进而得出答案.
解:﹣是一个数的相反数,这个数是:.
故选:C.
3.若|a+2|+|b﹣7|=0,则a+b的值为( )
A.﹣1 B.1 C.5 D.﹣5
【分析】根据非负数的性质分别求出a、b,计算即可.
解:∵|a+2|+|b﹣7|=0,
∴|a+2|=0,|b﹣7|=0,
∴a+2=0,b﹣7=0,
解得,a=﹣2,b=7,
则a+b=5,
故选:C.
4.根据直线、射线、线段的性质,图中的各组直线、射线、线段一定能相交的是( )
A. B.
C. D.
【分析】根据射线能够向一方延伸,直线能够向两方延伸和线段不能延伸进行分析.
解:根据直线、射线、线段的延伸性,知C一定能够相交.
故选:C.
5.下列说法正确的是( )
A.角的大小和开口的大小无关
B.互余、互补是指两个角之间的数量关系
C.单独的一个角也可以叫余角或补角
D.若三个角的和是直角,则他们互余
【分析】判断两角的关系,可根据角的性质,两角互余,和为90°,互补和为180°,据此可解出本题.
解:A、角的大小和开口的大小有关,此选项是错误的;
B、互余、互补是指两个角之间的数量关系,此选项正确;
C、两角互余和为90°,互补和为180°,所以此选项错误;
D、两角互余和为90°,所以此选项错误.
故选:B.
6.如图,已知直线AB、CD相交于点O,OA平分∠EOC,∠EOC=110°,则∠BOD的度数是( )
A.25° B.35° C.45° D.55°
【分析】根据角平分线的定义求出∠AOC的度数,再根据对顶角相等即可求解.
解:∵OA平分∠EOC,∠EOC=110°,
∴∠AOC=∠COE=55°,
∴∠BOD=∠AOC=55°.
故选:D.
7.如图,若A是实数a在数轴上对应的点,则关于a,﹣a,1的大小关系表示正确的是( )
A.a<1<﹣a B.a<﹣a<1 C.1<﹣a<a D.﹣a<a<1
【分析】根据数轴可以得到a<1<﹣a,据此即可确定哪个选项正确.
解:∵实数a在数轴上原点的左边,
∴a<0,但|a|>1,﹣a>1,
则有a<1<﹣a.
故选:A.
8.在直线l上顺次取A、B、C三点,使得AB=5cm,BC=3cm,如果O是线段AC的中点,那么线段OB的长度是( )
A.0.5 cm B.1 cm C.1.5 cm D.2 cm
【分析】根据题意画出图形,再根据OB=OC﹣BC=AC﹣BC解答即可.
解:如图所示:
∵AB=5cm,BC=3cm,O是线段AC的中点,
∴OB=OC﹣BC=AC﹣BC=(AB+BC)﹣BC=(5+3)﹣3=4﹣3=1cm.
故选:B.
9.下面等式成立的是( )
A.83.5°=83°50′ B.37°12′36″=37.48°
C.24°24′24″=24.44° D.41.25°=41°15′
【分析】进行度、分、秒的加法、减法计算,注意以60为进制.
解:A、83.5°=83°30′,错误;
B、37°12′36″=37.21°,错误;
C、24°24′24″=24.4°,错误;
D、41.25°=41°15′,正确.
故选:D.
10.当分针指向12,时针这时恰好与分针成30°的角,此时是( )
A.9点钟 B.10点钟
C.11点钟或1点钟 D.2点钟或10点钟
【分析】根据钟表上每一个大格之间的夹角是30°,当分针指向12,时针这时恰好与分针成30°的角,应该得出,时针距分针应该是1个格,应考虑两种情况.
解:∵钟表上每一个大格之间的夹角是30°,
∴当分针指向12,时针这时恰好与分针成30°的角时,距分针成30°的角时针应该有两种情况,即距时针1个格,
∴只有11点钟或1点钟是符合要求.
故选:C.
11.小明做了以下4道计算题:①(﹣1)2020+(﹣2)=﹣3;②0﹣(﹣1)=1;③﹣×=﹣;④÷(﹣)=﹣1.请你帮他检查一下,他一共做对了( )
A.4题 B.3题 C.2题 D.1题
【分析】根据有理数加减乘除的运算方法,以及有理数的混合运算的运算方法,逐项判断即可.
解:∵(﹣1)2020+(﹣2)=﹣1,
∴选项①不符合题意;
∵0﹣(﹣1)=1,
∴选项②符合题意;
∵﹣×=﹣,
∴选项③符合题意;
∵÷(﹣)=﹣1,
∴选项④不符合题意,
∴他一共做对了3道:②、③、④.
故选:B.
12.如图,将△ABC就点C按逆时针方向旋转75°后得到△A′B′C,若∠ACB=25°,则∠BCA′的度数为( )
A.50° B.40° C.25° D.60°
【分析】易知旋转角∠ACA′=75°,则根据∠BCA′=∠ACA′﹣∠ACB即可.
解:根据旋转的定义可知旋转角∠ACA′=75°,
∴∠BCA′=∠ACA′﹣∠ACB=75°﹣25°=50°.
故选:A.
13.下面是黑板上出示的尺规作图题,需要回答符号代表的内容( )
如图,已知∠AOB,求作:∠DEF,使∠DEF=∠AOB作法:(1)以为圆心,任意长为半径画弧,分别交OA、OB于点P、Q;(2)作射线EG,并以点E为圆心长为半径画弧交EG于点D;(3)以点D为圆心长为半径画弧交(2)步中所画弧于点F;(4)作,∠DEF即为所求作的角.
A.表示点E B.表示PQ C.表示OQ D.表示射线EF
【分析】根据尺规作图作一个角等于已知角的方法即可判断.
解:作法:(1)以点O为圆心,任意长为半径画弧,分别交OA、OB于点P、Q;
(2)作射线EG,并以点E为圆心OP长为半径画弧交EG于点D;
(3)以点D为圆心PQ长为半径画弧交(2)步中所画弧于点F;
(4)作射线EF,∠DEF即为所求作的角.
所以A,B,C选项都错误,D选项正确.
故选:D.
14.在算式3﹣|﹣1□2|中的“□”里,选择一个运算符号,使得算式的值最大( )
A.+ B.﹣ C.× D.÷
【分析】根据题意,要使得算式的值最大,就要使﹣1□2的绝对值最小,所以选择的运算符号是÷,据此判断即可.
解:在算式3﹣|﹣1□2|中的“□”里,要使得算式的值最大,就要使﹣1□2的绝对值最小,
∴选择的运算符号是÷.
故选:D.
15.如图,在正方形ABCD中,E为DC边上一点,沿线段BE对折后,若∠ABF比∠EBF大15°,则∠EBC的度数是( )
A.15° B.20° C.25° D.30°
【分析】根据翻折变换可得∠EBC=∠FBE,再由正方形的性质得出∠ABC=90°,设未知数,列方程求解即可.
解:由翻折变换可知,∠EBC=∠FBE,
设∠EBC=x,则∠ABF=15°+x,
∵四边形ABCD是正方形,
∴∠ABC=90°,
∴x+x+15°+x=90°,
解得x=25°,
故选:C.
16.如图,∠AOB=α,OA1、OB1分别是∠AOM和∠MOB的平分线,OA2、OB2分别是∠A1OM和∠MOB1的平分线,OA3、OB3分别是∠A2OM和∠MOB2的平分线,…,OAn,OBn分别是∠An﹣1OM和∠MOBn﹣1的平分线,则∠AnOBn的度数是( )
A. B. C. D.
【分析】根据角平分线的性质分别表示出∠A1OB1、∠A2OB2、…,即可归纳出此题规律,求得此题结果.
解:∵OA1、OB1分别是∠AOM和∠MOB的平分线,
∴∠A1OM=∠AOM,∠B1OM=∠BOM,
∴∠A1OB1=∠A1OM+∠B1OM=∠AOM+∠BOM=(∠AOM+B0M)=∠AOB=α,
同理,∠A2OB2=∠A1OB1=×α=α,
∠A3OB3=∠A2OB2=×α=α,
…
∴∠AnOBn=,
故选:C.
二、填空题(本大题有3个小题,共10分;17,18小题3分;19小题有2个空,每空2分,把答案写在题中横线上)
17.如果a、b互为倒数,c、d互为相反数,且m=﹣1,则代数式2ab﹣(c+d)+m2= 3 .
【分析】如果a、b互为倒数,则ab=1,c、d互为相反数,则c+d=0,且m=﹣1,直接代入即可求出所求的结果.
解:∵ab=1,c+d=0,m=﹣1,
∴2ab﹣(c+d)+m2=2﹣0+1=3.
18.如图所示,C、D是线段AB上两点,若AC=3,C为线段AD中点且AB=10,则线段DB长是 4 .
【分析】由已知中点可求AD=6,再由AB=10即可求BD.
解:∵AC=3,C为线段AD中点,
∴CD=3,
∴AD=6,
∵AB=10,
∴BD=4;
故答案为4.
19.数学家发明了一个魔术盒,当任意数对(a,b)放入其中时,会得到一个新的数:a2+b+1.例如把(3,﹣2)放入其中,就会得到32+(﹣2)+1=8.现将数对(﹣2,3)放入其中得到数m= 8 ,再将数对(m,1)放入其中后,得到的数是 66 .
【分析】根据题中的新定义化简所求式子,计算即可得到结果.
解:数对(﹣2,3)放入其中得到(﹣2)2+3+1=4+3+1=8;
再将数对(8,1)放入其中得到m2+1+1=82+1+1=64+1+1=66.
故答案为:8;66.
三、解答题(本大题有6个小题,共5分,解答应写出文字说明、证明过程或演算步骤)
20.(1)计算:11﹣18﹣12+19.
(2)计算:﹣12+2014×(﹣)3×0﹣(﹣3).
【分析】(1)直接利用有理数的加减运算法则计算得出答案;
(2)直接利用有理数的混合运算法则,先算乘方,再算乘除,后算加减,进而得出答案.
解:(1)11﹣18﹣12+19
=(11+19)+(﹣18﹣12)
=30﹣30
=0;
( 2)原式=﹣1+0+3
=2.
21.计算:
(1);
(2).
【分析】(1)直接利用乘法分配律化简,再利用有理数的加减运算法则计算得出答案;
(2)直接利用有理数的混合运算法则,先算乘方,再算乘除,后算加减,进而得出答案.
解:(1)原式=×(﹣48)+×(﹣48)﹣×(﹣48)+×(﹣48)
=
=;
(2)原式=
=
=﹣9+0
=﹣9.
22.如图,已知线段AB,按下列要求完成画图和计算:
(1)延长线段AB到点C,使BC=3AB(尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,如果点D为线段BC的中点,且AB=2,求线段AD的长度;
(3)在以上的条件下,若点P从A点出发,以每秒1个单位长度的速度向点C移动,到点C时停止.设点P的运动时间为t秒,是否存在某时刻t,使得PB=PA﹣PC?若存在,求出时间t:若不存在,请说明理由.
【分析】(1)延长线段AB到点C,使BC=3AB即可;
(2)在(1)的条件下,如果点D为线段BC的中点,且AB=2,即可求线段AD的长度;
(3)在以上的条件下,若点P从A点出发,以每秒1个单位长度的速度向点C移动,到点C时停止.设点P的运动时间为t秒,是否存在某时刻t,使得PB=PA﹣PC?即可求出时间t.
解:如图所示,
(1)延长线段AB到点C,使BC=3AB;
(2)∵AB=2,
∴BC=3AB=6,
∵点D为线段BC的中点,
∴BD=BC=3,
∴AD=AB+BD=5.
答:线段AD的长度为5;
(3)点P从A点出发,以每秒1个单位长度的速度向点C移动,到点C时停止.
设点P的运动时间为t秒,
则PB=|t﹣2|,PA=t,PC=8﹣t,
PB=PA﹣PC
即|t﹣2|=t﹣(8﹣t)
解得t=6或.
但是当t=时,PA﹣PC=t﹣(8﹣t)=2t﹣8=﹣,不符合题意,舍去.
答:时间t为6.
23.某检修小组从A地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶记录如下.(单位:千米)
第一次 第二次 第三次 第四次 第五次 第六次 第七次
﹣4 +7 ﹣9 +8 +6 ﹣5 ﹣2
(1)求收工时距A地多远?
(2)在第几次记录时距A地最远?距离A多远?
(3)若每千米耗油0.3升,问共耗油多少升?
【分析】(1)把所有数值相加即可,若结果得正,就说明在A地的东面,若结果为负,则说明在A地的西面;
(2)通过观察可知,当算到第五次时,应该是距A地最远,把第一次到第五次的数值相加即可;
(3)先计算所有数值的绝对值之和,再乘以0.3即可.
解:(1)﹣4+7﹣9+8+6﹣5﹣2=+1,
答:收工时在A的东面,距A地1千米;
(2)﹣4+7﹣9+8+6=8,
答:在第五次记录时距A地最远,距离A地8米;
(3)|﹣4|+|+7|+|﹣9|+|+8|+|+6|+|﹣5|+|﹣2|=41,
41×0.3=12.3(升)
答:共耗油12.3升.
24.如图所示,观察数轴,请回答:
(1)点C与点D的距离为 3 ,点B与点D的距离为 2 ;
点B与点E的距离为 4 ,点C与点A的距离为 7 ;
(2)发现:在数轴上,如果点M与点N分别表示数m,n,则它们之间的距离可表示为MN= |m﹣n| (用m,n表示);
(3)利用发现的结论,逆向思维解决下列问题:
①数轴上表示x的点P与B之间的距离是1,则x的值是 ﹣3或﹣1 ;
②|x+3|=2,则x= ﹣5或﹣1 ;
③数轴上是否存在表示x的点P,使点P到点B、点C的距离之和为11?若存在,请求出x的值;若不存在,说明理由;
④|x+2|+|x﹣7|的最小值为 9 ;
【分析】(1)观察数轴可得答案;
(2)观察数轴并结合(1)的计算可得答案;
(3)①根据(2)中结论,可列方程解得答案;
②根据数轴上两点间的距离的含义或根据绝对值的化简法则,可求得答案;
③分类列出关于x的一元一次方程并求解即可;
④根据数轴上的点之间的距离,可得答案.
解:(1)观察数轴可得:点C与点D的距离为3,点B与点D的距离为2;
点B与点E的距离为4,点C与点A的距离为7;
故答案为:3,2;4,7;
(2)观察数轴并结合(1)中运算可得MN=|m﹣n|;
故答案为:|m﹣n|;
(3)①由(1)可知,数轴上表示x和﹣2的两点P与B之间的距离是1,则|x+2|=1,
解得:x=﹣3或x=﹣1.
故答案为:﹣3或﹣1;
②|x+3|=2,即x+3=2或x+3=﹣2,
解得:x=﹣1或﹣5,
故答案为:﹣5或﹣1;
③存在.理由如下:
若P点在B点左侧,﹣2﹣x+3﹣x=11,解得x=﹣5;
若P点在B、C之间,x+2+3﹣x=11,此方程不成立;
若P点在C点右侧,x+2+x﹣3=11,解得x=6.
答:存在.x的值为﹣5或6;
④∵|x+2|+|x﹣7|为表示数x的点与表示﹣2和7两个点的距离之和
∴当表示数x的点位于表示﹣2和7两个点之间时,有最小值9.
故答案为:9.
25.已知,如图1,把直角三角形MON的直角顶点O放在直线AB上,射线OC平分∠AON.
(1)如图1,若∠MOC=28°,求∠BON的度数;
(2)若将三角形MON绕点O旋转到如图2所示的位置,若∠BON=100°,则∠MOC的度数为 50° ;
(3)若将三角形MON绕点O旋转到如图3所示的位置,试写出∠BON和∠MOC之间的数量关系,并说明理由.
【分析】(1)根据角平分线和互为余角的意义,可求出∠NOC、∠AOC,再根据互为补角求出∠BON即可;
(2)根据补角的定义以及角平分线的定义求解即可;
(3)根据角平分线和互为余角的意义可得∠AOC=∠NOC=90°﹣∠MOC,再根据互为补角的意义得到∠BON=180°﹣2∠NOC=180°﹣2(90°﹣∠MOC)=2∠MOC.
解:(1)如图1,∵∠MOC=28°,∠MON=90°,
∴∠NOC=90°﹣28°=62°,
又∵OC平分∠AON,
∴∠AOC=∠NOC=62°,
∴∠BON=180°﹣2∠NOC=180°﹣62°×2=56°;
(2)∵∠BON=100°,
∴∠AON=80°,
∴∠AOM=90°﹣∠AON=10°,∠AOC=40°,
∴∠MOC=∠AOM+∠AOC=50°.
故答案为:50°;
(3)∠BON=2∠MOC,
如图2,∵OC平分∠AON,
∴∠AOC=∠NOC,
∵∠MON=90°,
∴∠AOC=∠NOC=90°﹣∠MOC,
∴∠BON=180°﹣2∠NOC=180°﹣2(90°﹣∠MOC)=2∠MOC,
即:∠BON=2∠MOC.
一、选择题:(本大题有16个小题,每小题2分,共32分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.如果将向东行驶3km记作+3km,那么向西行驶2km应记作( )
A.+2km B.﹣2km C.+3km D.﹣3km
2.﹣是一个数的相反数,这个数是( )
A.2 B.﹣2 C. D.﹣
3.若|a+2|+|b﹣7|=0,则a+b的值为( )
A.﹣1 B.1 C.5 D.﹣5
4.根据直线、射线、线段的性质,图中的各组直线、射线、线段一定能相交的是( )
A. B.
C. D.
5.下列说法正确的是( )
A.角的大小和开口的大小无关
B.互余、互补是指两个角之间的数量关系
C.单独的一个角也可以叫余角或补角
D.若三个角的和是直角,则他们互余
6.如图,已知直线AB、CD相交于点O,OA平分∠EOC,∠EOC=110°,则∠BOD的度数是( )
A.25° B.35° C.45° D.55°
7.如图,若A是实数a在数轴上对应的点,则关于a,﹣a,1的大小关系表示正确的是( )
A.a<1<﹣a B.a<﹣a<1 C.1<﹣a<a D.﹣a<a<1
8.在直线l上顺次取A、B、C三点,使得AB=5cm,BC=3cm,如果O是线段AC的中点,那么线段OB的长度是( )
A.0.5 cm B.1 cm C.1.5 cm D.2 cm
9.下面等式成立的是( )
A.83.5°=83°50′ B.37°12′36″=37.48°
C.24°24′24″=24.44° D.41.25°=41°15′
10.当分针指向12,时针这时恰好与分针成30°的角,此时是( )
A.9点钟 B.10点钟
C.11点钟或1点钟 D.2点钟或10点钟
11.小明做了以下4道计算题:①(﹣1)2020+(﹣2)=﹣3;②0﹣(﹣1)=1;③﹣×=﹣;④÷(﹣)=﹣1.请你帮他检查一下,他一共做对了( )
A.4题 B.3题 C.2题 D.1题
12.如图,将△ABC就点C按逆时针方向旋转75°后得到△A′B′C,若∠ACB=25°,则∠BCA′的度数为( )
A.50° B.40° C.25° D.60°
13.下面是黑板上出示的尺规作图题,需要回答符号代表的内容( )
如图,已知∠AOB,求作:∠DEF,使∠DEF=∠AOB作法:(1)以为圆心,任意长为半径画弧,分别交OA、OB于点P、Q;(2)作射线EG,并以点E为圆心长为半径画弧交EG于点D;(3)以点D为圆心长为半径画弧交(2)步中所画弧于点F;(4)作,∠DEF即为所求作的角.
A.表示点E B.表示PQ C.表示OQ D.表示射线EF
14.在算式3﹣|﹣1□2|中的“□”里,选择一个运算符号,使得算式的值最大( )
A.+ B.﹣ C.× D.÷
15.如图,在正方形ABCD中,E为DC边上一点,沿线段BE对折后,若∠ABF比∠EBF大15°,则∠EBC的度数是( )
A.15° B.20° C.25° D.30°
16.如图,∠AOB=α,OA1、OB1分别是∠AOM和∠MOB的平分线,OA2、OB2分别是∠A1OM和∠MOB1的平分线,OA3、OB3分别是∠A2OM和∠MOB2的平分线,…,OAn,OBn分别是∠An﹣1OM和∠MOBn﹣1的平分线,则∠AnOBn的度数是( )
A. B. C. D.
二、填空题(本大题有3个小题,共10分;17,18小题3分;19小题有2个空,每空2分,把答案写在题中横线上)
17.如果a、b互为倒数,c、d互为相反数,且m=﹣1,则代数式2ab﹣(c+d)+m2= .
18.如图所示,C、D是线段AB上两点,若AC=3,C为线段AD中点且AB=10,则线段DB长是 .
19.数学家发明了一个魔术盒,当任意数对(a,b)放入其中时,会得到一个新的数:a2+b+1.例如把(3,﹣2)放入其中,就会得到32+(﹣2)+1=8.现将数对(﹣2,3)放入其中得到数m= ,再将数对(m,1)放入其中后,得到的数是 .
三、解答题(本大题有6个小题,共5分,解答应写出文字说明、证明过程或演算步骤)
20.(1)计算:11﹣18﹣12+19.
(2)计算:﹣12+2014×(﹣)3×0﹣(﹣3).
21.计算:
(1);
(2).
22.如图,已知线段AB,按下列要求完成画图和计算:
(1)延长线段AB到点C,使BC=3AB(尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,如果点D为线段BC的中点,且AB=2,求线段AD的长度;
(3)在以上的条件下,若点P从A点出发,以每秒1个单位长度的速度向点C移动,到点C时停止.设点P的运动时间为t秒,是否存在某时刻t,使得PB=PA﹣PC?若存在,求出时间t:若不存在,请说明理由.
23.某检修小组从A地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶记录如下.(单位:千米)
第一次 第二次 第三次 第四次 第五次 第六次 第七次
﹣4 +7 ﹣9 +8 +6 ﹣5 ﹣2
(1)求收工时距A地多远?
(2)在第几次记录时距A地最远?距离A多远?
(3)若每千米耗油0.3升,问共耗油多少升?
24.如图所示,观察数轴,请回答:
(1)点C与点D的距离为 ,点B与点D的距离为 ;
点B与点E的距离为 ,点C与点A的距离为 ;
(2)发现:在数轴上,如果点M与点N分别表示数m,n,则它们之间的距离可表示为MN= (用m,n表示);
(3)利用发现的结论,逆向思维解决下列问题:
①数轴上表示x的点P与B之间的距离是1,则x的值是 ;
②|x+3|=2,则x= ;
③数轴上是否存在表示x的点P,使点P到点B、点C的距离之和为11?若存在,请求出x的值;若不存在,说明理由;
④|x+2|+|x﹣7|的最小值为 ;
25.已知,如图1,把直角三角形MON的直角顶点O放在直线AB上,射线OC平分∠AON.
(1)如图1,若∠MOC=28°,求∠BON的度数;
(2)若将三角形MON绕点O旋转到如图2所示的位置,若∠BON=100°,则∠MOC的度数为 ;
(3)若将三角形MON绕点O旋转到如图3所示的位置,试写出∠BON和∠MOC之间的数量关系,并说明理由.
参考答案
一、选择题:(本大题有16个小题,每小题2分,共32分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.如果将向东行驶3km记作+3km,那么向西行驶2km应记作( )
A.+2km B.﹣2km C.+3km D.﹣3km
【分析】根据正数和负数表示相反意义的量,向东记为正,可得答案.
解:向东行驶3km,记作+3km,向西行驶2km记作﹣2km,
故选:B.
2.﹣是一个数的相反数,这个数是( )
A.2 B.﹣2 C. D.﹣
【分析】根据相反数的概念:只有符号不同的两个数叫做互为相反数,进而得出答案.
解:﹣是一个数的相反数,这个数是:.
故选:C.
3.若|a+2|+|b﹣7|=0,则a+b的值为( )
A.﹣1 B.1 C.5 D.﹣5
【分析】根据非负数的性质分别求出a、b,计算即可.
解:∵|a+2|+|b﹣7|=0,
∴|a+2|=0,|b﹣7|=0,
∴a+2=0,b﹣7=0,
解得,a=﹣2,b=7,
则a+b=5,
故选:C.
4.根据直线、射线、线段的性质,图中的各组直线、射线、线段一定能相交的是( )
A. B.
C. D.
【分析】根据射线能够向一方延伸,直线能够向两方延伸和线段不能延伸进行分析.
解:根据直线、射线、线段的延伸性,知C一定能够相交.
故选:C.
5.下列说法正确的是( )
A.角的大小和开口的大小无关
B.互余、互补是指两个角之间的数量关系
C.单独的一个角也可以叫余角或补角
D.若三个角的和是直角,则他们互余
【分析】判断两角的关系,可根据角的性质,两角互余,和为90°,互补和为180°,据此可解出本题.
解:A、角的大小和开口的大小有关,此选项是错误的;
B、互余、互补是指两个角之间的数量关系,此选项正确;
C、两角互余和为90°,互补和为180°,所以此选项错误;
D、两角互余和为90°,所以此选项错误.
故选:B.
6.如图,已知直线AB、CD相交于点O,OA平分∠EOC,∠EOC=110°,则∠BOD的度数是( )
A.25° B.35° C.45° D.55°
【分析】根据角平分线的定义求出∠AOC的度数,再根据对顶角相等即可求解.
解:∵OA平分∠EOC,∠EOC=110°,
∴∠AOC=∠COE=55°,
∴∠BOD=∠AOC=55°.
故选:D.
7.如图,若A是实数a在数轴上对应的点,则关于a,﹣a,1的大小关系表示正确的是( )
A.a<1<﹣a B.a<﹣a<1 C.1<﹣a<a D.﹣a<a<1
【分析】根据数轴可以得到a<1<﹣a,据此即可确定哪个选项正确.
解:∵实数a在数轴上原点的左边,
∴a<0,但|a|>1,﹣a>1,
则有a<1<﹣a.
故选:A.
8.在直线l上顺次取A、B、C三点,使得AB=5cm,BC=3cm,如果O是线段AC的中点,那么线段OB的长度是( )
A.0.5 cm B.1 cm C.1.5 cm D.2 cm
【分析】根据题意画出图形,再根据OB=OC﹣BC=AC﹣BC解答即可.
解:如图所示:
∵AB=5cm,BC=3cm,O是线段AC的中点,
∴OB=OC﹣BC=AC﹣BC=(AB+BC)﹣BC=(5+3)﹣3=4﹣3=1cm.
故选:B.
9.下面等式成立的是( )
A.83.5°=83°50′ B.37°12′36″=37.48°
C.24°24′24″=24.44° D.41.25°=41°15′
【分析】进行度、分、秒的加法、减法计算,注意以60为进制.
解:A、83.5°=83°30′,错误;
B、37°12′36″=37.21°,错误;
C、24°24′24″=24.4°,错误;
D、41.25°=41°15′,正确.
故选:D.
10.当分针指向12,时针这时恰好与分针成30°的角,此时是( )
A.9点钟 B.10点钟
C.11点钟或1点钟 D.2点钟或10点钟
【分析】根据钟表上每一个大格之间的夹角是30°,当分针指向12,时针这时恰好与分针成30°的角,应该得出,时针距分针应该是1个格,应考虑两种情况.
解:∵钟表上每一个大格之间的夹角是30°,
∴当分针指向12,时针这时恰好与分针成30°的角时,距分针成30°的角时针应该有两种情况,即距时针1个格,
∴只有11点钟或1点钟是符合要求.
故选:C.
11.小明做了以下4道计算题:①(﹣1)2020+(﹣2)=﹣3;②0﹣(﹣1)=1;③﹣×=﹣;④÷(﹣)=﹣1.请你帮他检查一下,他一共做对了( )
A.4题 B.3题 C.2题 D.1题
【分析】根据有理数加减乘除的运算方法,以及有理数的混合运算的运算方法,逐项判断即可.
解:∵(﹣1)2020+(﹣2)=﹣1,
∴选项①不符合题意;
∵0﹣(﹣1)=1,
∴选项②符合题意;
∵﹣×=﹣,
∴选项③符合题意;
∵÷(﹣)=﹣1,
∴选项④不符合题意,
∴他一共做对了3道:②、③、④.
故选:B.
12.如图,将△ABC就点C按逆时针方向旋转75°后得到△A′B′C,若∠ACB=25°,则∠BCA′的度数为( )
A.50° B.40° C.25° D.60°
【分析】易知旋转角∠ACA′=75°,则根据∠BCA′=∠ACA′﹣∠ACB即可.
解:根据旋转的定义可知旋转角∠ACA′=75°,
∴∠BCA′=∠ACA′﹣∠ACB=75°﹣25°=50°.
故选:A.
13.下面是黑板上出示的尺规作图题,需要回答符号代表的内容( )
如图,已知∠AOB,求作:∠DEF,使∠DEF=∠AOB作法:(1)以为圆心,任意长为半径画弧,分别交OA、OB于点P、Q;(2)作射线EG,并以点E为圆心长为半径画弧交EG于点D;(3)以点D为圆心长为半径画弧交(2)步中所画弧于点F;(4)作,∠DEF即为所求作的角.
A.表示点E B.表示PQ C.表示OQ D.表示射线EF
【分析】根据尺规作图作一个角等于已知角的方法即可判断.
解:作法:(1)以点O为圆心,任意长为半径画弧,分别交OA、OB于点P、Q;
(2)作射线EG,并以点E为圆心OP长为半径画弧交EG于点D;
(3)以点D为圆心PQ长为半径画弧交(2)步中所画弧于点F;
(4)作射线EF,∠DEF即为所求作的角.
所以A,B,C选项都错误,D选项正确.
故选:D.
14.在算式3﹣|﹣1□2|中的“□”里,选择一个运算符号,使得算式的值最大( )
A.+ B.﹣ C.× D.÷
【分析】根据题意,要使得算式的值最大,就要使﹣1□2的绝对值最小,所以选择的运算符号是÷,据此判断即可.
解:在算式3﹣|﹣1□2|中的“□”里,要使得算式的值最大,就要使﹣1□2的绝对值最小,
∴选择的运算符号是÷.
故选:D.
15.如图,在正方形ABCD中,E为DC边上一点,沿线段BE对折后,若∠ABF比∠EBF大15°,则∠EBC的度数是( )
A.15° B.20° C.25° D.30°
【分析】根据翻折变换可得∠EBC=∠FBE,再由正方形的性质得出∠ABC=90°,设未知数,列方程求解即可.
解:由翻折变换可知,∠EBC=∠FBE,
设∠EBC=x,则∠ABF=15°+x,
∵四边形ABCD是正方形,
∴∠ABC=90°,
∴x+x+15°+x=90°,
解得x=25°,
故选:C.
16.如图,∠AOB=α,OA1、OB1分别是∠AOM和∠MOB的平分线,OA2、OB2分别是∠A1OM和∠MOB1的平分线,OA3、OB3分别是∠A2OM和∠MOB2的平分线,…,OAn,OBn分别是∠An﹣1OM和∠MOBn﹣1的平分线,则∠AnOBn的度数是( )
A. B. C. D.
【分析】根据角平分线的性质分别表示出∠A1OB1、∠A2OB2、…,即可归纳出此题规律,求得此题结果.
解:∵OA1、OB1分别是∠AOM和∠MOB的平分线,
∴∠A1OM=∠AOM,∠B1OM=∠BOM,
∴∠A1OB1=∠A1OM+∠B1OM=∠AOM+∠BOM=(∠AOM+B0M)=∠AOB=α,
同理,∠A2OB2=∠A1OB1=×α=α,
∠A3OB3=∠A2OB2=×α=α,
…
∴∠AnOBn=,
故选:C.
二、填空题(本大题有3个小题,共10分;17,18小题3分;19小题有2个空,每空2分,把答案写在题中横线上)
17.如果a、b互为倒数,c、d互为相反数,且m=﹣1,则代数式2ab﹣(c+d)+m2= 3 .
【分析】如果a、b互为倒数,则ab=1,c、d互为相反数,则c+d=0,且m=﹣1,直接代入即可求出所求的结果.
解:∵ab=1,c+d=0,m=﹣1,
∴2ab﹣(c+d)+m2=2﹣0+1=3.
18.如图所示,C、D是线段AB上两点,若AC=3,C为线段AD中点且AB=10,则线段DB长是 4 .
【分析】由已知中点可求AD=6,再由AB=10即可求BD.
解:∵AC=3,C为线段AD中点,
∴CD=3,
∴AD=6,
∵AB=10,
∴BD=4;
故答案为4.
19.数学家发明了一个魔术盒,当任意数对(a,b)放入其中时,会得到一个新的数:a2+b+1.例如把(3,﹣2)放入其中,就会得到32+(﹣2)+1=8.现将数对(﹣2,3)放入其中得到数m= 8 ,再将数对(m,1)放入其中后,得到的数是 66 .
【分析】根据题中的新定义化简所求式子,计算即可得到结果.
解:数对(﹣2,3)放入其中得到(﹣2)2+3+1=4+3+1=8;
再将数对(8,1)放入其中得到m2+1+1=82+1+1=64+1+1=66.
故答案为:8;66.
三、解答题(本大题有6个小题,共5分,解答应写出文字说明、证明过程或演算步骤)
20.(1)计算:11﹣18﹣12+19.
(2)计算:﹣12+2014×(﹣)3×0﹣(﹣3).
【分析】(1)直接利用有理数的加减运算法则计算得出答案;
(2)直接利用有理数的混合运算法则,先算乘方,再算乘除,后算加减,进而得出答案.
解:(1)11﹣18﹣12+19
=(11+19)+(﹣18﹣12)
=30﹣30
=0;
( 2)原式=﹣1+0+3
=2.
21.计算:
(1);
(2).
【分析】(1)直接利用乘法分配律化简,再利用有理数的加减运算法则计算得出答案;
(2)直接利用有理数的混合运算法则,先算乘方,再算乘除,后算加减,进而得出答案.
解:(1)原式=×(﹣48)+×(﹣48)﹣×(﹣48)+×(﹣48)
=
=;
(2)原式=
=
=﹣9+0
=﹣9.
22.如图,已知线段AB,按下列要求完成画图和计算:
(1)延长线段AB到点C,使BC=3AB(尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,如果点D为线段BC的中点,且AB=2,求线段AD的长度;
(3)在以上的条件下,若点P从A点出发,以每秒1个单位长度的速度向点C移动,到点C时停止.设点P的运动时间为t秒,是否存在某时刻t,使得PB=PA﹣PC?若存在,求出时间t:若不存在,请说明理由.
【分析】(1)延长线段AB到点C,使BC=3AB即可;
(2)在(1)的条件下,如果点D为线段BC的中点,且AB=2,即可求线段AD的长度;
(3)在以上的条件下,若点P从A点出发,以每秒1个单位长度的速度向点C移动,到点C时停止.设点P的运动时间为t秒,是否存在某时刻t,使得PB=PA﹣PC?即可求出时间t.
解:如图所示,
(1)延长线段AB到点C,使BC=3AB;
(2)∵AB=2,
∴BC=3AB=6,
∵点D为线段BC的中点,
∴BD=BC=3,
∴AD=AB+BD=5.
答:线段AD的长度为5;
(3)点P从A点出发,以每秒1个单位长度的速度向点C移动,到点C时停止.
设点P的运动时间为t秒,
则PB=|t﹣2|,PA=t,PC=8﹣t,
PB=PA﹣PC
即|t﹣2|=t﹣(8﹣t)
解得t=6或.
但是当t=时,PA﹣PC=t﹣(8﹣t)=2t﹣8=﹣,不符合题意,舍去.
答:时间t为6.
23.某检修小组从A地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶记录如下.(单位:千米)
第一次 第二次 第三次 第四次 第五次 第六次 第七次
﹣4 +7 ﹣9 +8 +6 ﹣5 ﹣2
(1)求收工时距A地多远?
(2)在第几次记录时距A地最远?距离A多远?
(3)若每千米耗油0.3升,问共耗油多少升?
【分析】(1)把所有数值相加即可,若结果得正,就说明在A地的东面,若结果为负,则说明在A地的西面;
(2)通过观察可知,当算到第五次时,应该是距A地最远,把第一次到第五次的数值相加即可;
(3)先计算所有数值的绝对值之和,再乘以0.3即可.
解:(1)﹣4+7﹣9+8+6﹣5﹣2=+1,
答:收工时在A的东面,距A地1千米;
(2)﹣4+7﹣9+8+6=8,
答:在第五次记录时距A地最远,距离A地8米;
(3)|﹣4|+|+7|+|﹣9|+|+8|+|+6|+|﹣5|+|﹣2|=41,
41×0.3=12.3(升)
答:共耗油12.3升.
24.如图所示,观察数轴,请回答:
(1)点C与点D的距离为 3 ,点B与点D的距离为 2 ;
点B与点E的距离为 4 ,点C与点A的距离为 7 ;
(2)发现:在数轴上,如果点M与点N分别表示数m,n,则它们之间的距离可表示为MN= |m﹣n| (用m,n表示);
(3)利用发现的结论,逆向思维解决下列问题:
①数轴上表示x的点P与B之间的距离是1,则x的值是 ﹣3或﹣1 ;
②|x+3|=2,则x= ﹣5或﹣1 ;
③数轴上是否存在表示x的点P,使点P到点B、点C的距离之和为11?若存在,请求出x的值;若不存在,说明理由;
④|x+2|+|x﹣7|的最小值为 9 ;
【分析】(1)观察数轴可得答案;
(2)观察数轴并结合(1)的计算可得答案;
(3)①根据(2)中结论,可列方程解得答案;
②根据数轴上两点间的距离的含义或根据绝对值的化简法则,可求得答案;
③分类列出关于x的一元一次方程并求解即可;
④根据数轴上的点之间的距离,可得答案.
解:(1)观察数轴可得:点C与点D的距离为3,点B与点D的距离为2;
点B与点E的距离为4,点C与点A的距离为7;
故答案为:3,2;4,7;
(2)观察数轴并结合(1)中运算可得MN=|m﹣n|;
故答案为:|m﹣n|;
(3)①由(1)可知,数轴上表示x和﹣2的两点P与B之间的距离是1,则|x+2|=1,
解得:x=﹣3或x=﹣1.
故答案为:﹣3或﹣1;
②|x+3|=2,即x+3=2或x+3=﹣2,
解得:x=﹣1或﹣5,
故答案为:﹣5或﹣1;
③存在.理由如下:
若P点在B点左侧,﹣2﹣x+3﹣x=11,解得x=﹣5;
若P点在B、C之间,x+2+3﹣x=11,此方程不成立;
若P点在C点右侧,x+2+x﹣3=11,解得x=6.
答:存在.x的值为﹣5或6;
④∵|x+2|+|x﹣7|为表示数x的点与表示﹣2和7两个点的距离之和
∴当表示数x的点位于表示﹣2和7两个点之间时,有最小值9.
故答案为:9.
25.已知,如图1,把直角三角形MON的直角顶点O放在直线AB上,射线OC平分∠AON.
(1)如图1,若∠MOC=28°,求∠BON的度数;
(2)若将三角形MON绕点O旋转到如图2所示的位置,若∠BON=100°,则∠MOC的度数为 50° ;
(3)若将三角形MON绕点O旋转到如图3所示的位置,试写出∠BON和∠MOC之间的数量关系,并说明理由.
【分析】(1)根据角平分线和互为余角的意义,可求出∠NOC、∠AOC,再根据互为补角求出∠BON即可;
(2)根据补角的定义以及角平分线的定义求解即可;
(3)根据角平分线和互为余角的意义可得∠AOC=∠NOC=90°﹣∠MOC,再根据互为补角的意义得到∠BON=180°﹣2∠NOC=180°﹣2(90°﹣∠MOC)=2∠MOC.
解:(1)如图1,∵∠MOC=28°,∠MON=90°,
∴∠NOC=90°﹣28°=62°,
又∵OC平分∠AON,
∴∠AOC=∠NOC=62°,
∴∠BON=180°﹣2∠NOC=180°﹣62°×2=56°;
(2)∵∠BON=100°,
∴∠AON=80°,
∴∠AOM=90°﹣∠AON=10°,∠AOC=40°,
∴∠MOC=∠AOM+∠AOC=50°.
故答案为:50°;
(3)∠BON=2∠MOC,
如图2,∵OC平分∠AON,
∴∠AOC=∠NOC,
∵∠MON=90°,
∴∠AOC=∠NOC=90°﹣∠MOC,
∴∠BON=180°﹣2∠NOC=180°﹣2(90°﹣∠MOC)=2∠MOC,
即:∠BON=2∠MOC.
同课章节目录
