沪科版初中数学八年级上册第11-14章复习测试题(word版 含解析)
文档属性
| 名称 | 沪科版初中数学八年级上册第11-14章复习测试题(word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 305.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 15:00:32 | ||
图片预览



文档简介
沪科版初中数学八年级上册第11-14章复习测试题
考试时间:120分钟 满分:120分
姓名:__________ 班级:__________考号:__________
一、单选题(共10题;共30分)
1. ( 3分 ) 在同一坐标系中,一次函数y=一mx+n2与二次函数y=x2+m的图象可能是( )
A. B. C. D.
2. ( 3分 ) 一次函数y=kx+b的图象经过点A(2,3),每当x增加1个单位时,y增加3个单位,则此函数表达式是( )
A. y=3x+3 B. y=2x﹣3 C. y=3x﹣3 D. y=3x﹣2
3. ( 3分 ) 如图,将三角板的直角顶点放在直尺的一边上, , , ( )度
A. 10 B. 20 C. 30 D. 50
4. ( 3分 ) 若一次函数y=(2m﹣3)x﹣1+m的图象不经过第三象限,则m的取值范图是( )
A. 1<m< B. 1≤m< C. 1<m≤ D. 1≤m≤
5. ( 3分 ) 如图,小明从A地前往B地,到达后立刻返回,他与A地的距离 千米 和所用时间 小时 之间的函数关系如图所示,则小明出发6小时后距A地
A. 120千米 B. 160千米 C. 180千米 D. 200千米
6. ( 3分 ) 在平面直角坐标系 中,已知点 关于关于x轴、y轴的对称点分别为P、Q若坐标轴上的点M恰使△MAP、△MAQ均为等腰三角形,则满足条件的M点有( )
A. 5 B. 6 C. 7 D. 9
7. ( 3分 ) 如图,在 中, , 为 上一点,且 ,又 的面积为10,则 的长是( )
A. 2 B. 3 C. 4 D. 5
8. ( 3分 ) 如下图,已知 , ,下列条件中不能判定 ≌ 的是( )
A. B. C. D.
9. ( 3分 ) 若点(m,n)在函数y=2x+1的图象上,则代数式4m﹣2n+1的值是( )
A. 1 B. ﹣1 C. 2 D. ﹣2
10. ( 3分 ) 在一次函数y=(2m﹣1)x+1中,y的值随着x值的增大而减小,则它的图象不经过( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
二、填空题(共10题;共20分)
11. ( 2分 ) 如图,在平面直角坐标系中,长方形OABC的边OA 在x轴上,OC在y轴上,OA=1,OC=2,对角线 AC的垂直平分线交AB 于点E,交AC于点D.若y轴上有一点P(不与点C重合),能使△AEP是以为 AE 为腰的等腰三角形,则点 P的坐标为 .
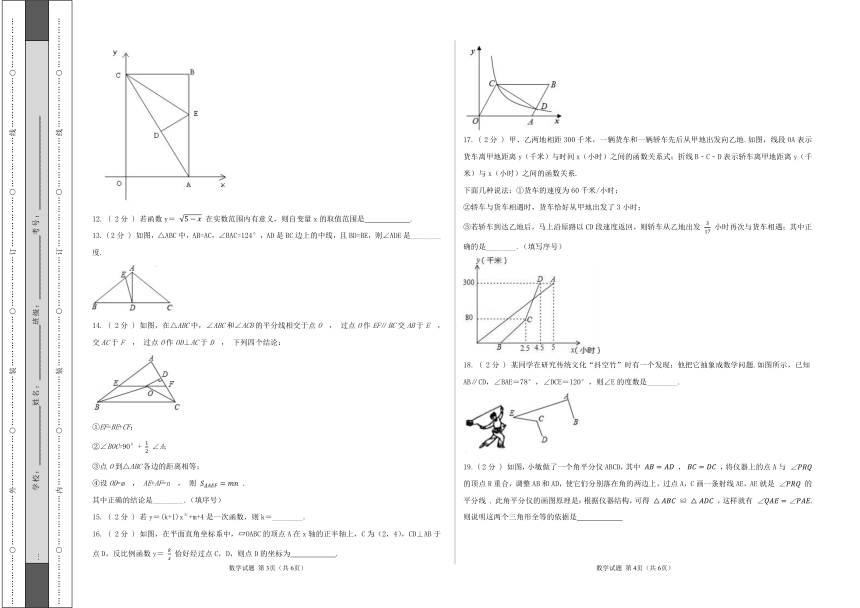
12. ( 2分 ) 若函数y= 在实数范围内有意义,则自变量x的取值范围是 .
13. ( 2分 ) 如图,△ABC中,AB=AC,∠BAC=124°,AD是BC边上的中线,且BD=BE,则∠ADE是________度.
14. ( 2分 ) 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O , 过点O作EF∥BC交AB于E , 交AC于F , 过点O作OD⊥AC于D , 下列四个结论:
①EF=BE+CF;
②∠BOC=90°+ ∠A;
③点O到△ABC各边的距离相等;
④设OD=m , AE+AF=n , 则 .
其中正确的结论是________.(填序号)
15. ( 2分 ) 若y=(k+1)x|k|+m+4是一次函数,则k=________.
16. ( 2分 ) 如图,在平面直角坐标系中, OABC的顶点A在x轴的正半轴上,C为(2,4),CD⊥AB于点D,反比例函数y= 恰好经过点C,D,则点D的坐标为 .
17. ( 2分 ) 甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地.如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系式;折线B﹣C﹣D表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.
下面几种说法:①货车的速度为60千米/小时;
②轿车与货车相遇时,货车恰好从甲地出发了3小时;
③若轿车到达乙地后,马上沿原路以CD段速度返回,则轿车从乙地出发 小时再次与货车相遇;其中正确的是________.(填写序号)
18. ( 2分 ) 某同学在研究传统文化“抖空竹”时有一个发现:他把它抽象成数学问题.如图所示,已知AB∥CD,∠BAE=78°,∠DCE=120°,则∠E的度数是________.
19. ( 2分 ) 如图,小敏做了一个角平分仪ABCD,其中 , ,将仪器上的点A与 的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是 的平分线 此角平分仪的画图原理是:根据仪器结构,可得 ≌ ,这样就有 则说明这两个三角形全等的依据是
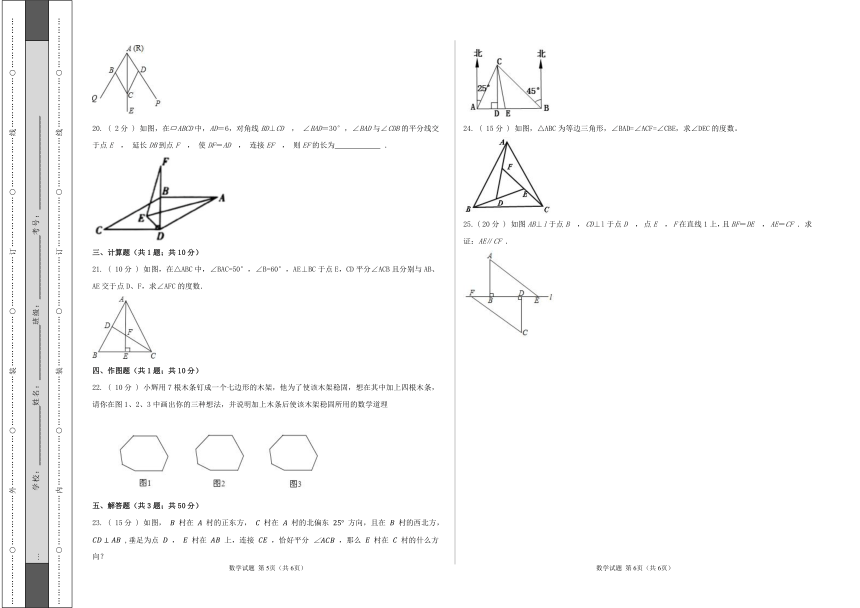
20. ( 2分 ) 如图,在 ABCD中,AD=6,对角线BD⊥CD , ∠BAD=30°,∠BAD与∠CDB的平分线交于点E , 延长DB到点F , 使DF=AD , 连接EF , 则EF的长为 .
三、计算题(共1题;共10分)
21. ( 10分 ) 如图,在△ABC中,∠BAC=50°,∠B=60°,AE⊥BC于点E,CD平分∠ACB且分别与AB、AE交于点D、F,求∠AFC的度数.
四、作图题(共1题;共10分)
22. ( 10分 ) 小辉用7根木条钉成一个七边形的木架,他为了使该木架稳固,想在其中加上四根木条,请你在图1、2、3中画出你的三种想法,并说明加上木条后使该木架稳固所用的数学道理
五、解答题(共3题;共50分)
23. ( 15分 ) 如图, 村在 村的正东方, 村在 村的北偏东 方向,且在 村的西北方, ,垂足为点 , 村在 上,连接 ,恰好平分 ,那么 村在 村的什么方向?
24. ( 15分 ) 如图,△ABC为等边三角形,∠BAD=∠ACF=∠CBE,求∠DEC的度数。
25. ( 20分 ) 如图AB⊥l于点B , CD⊥l于点D , 点E , F在直线1上,且BF=DE , AE=CF . 求证:AE∥CF .
数学试题 第3页(共4页) 数学试题 第4页(共4页)
数学试题 第1页(共6页) 数学试题 第2页(共6页)
答案解析部分
一、单选题
1.【答案】 D
【解析】解:∵ 一次函数y=-mx+n2 , 抛物线y=x2+m
n2>0,
∴此函数与y轴交于正半轴,且抛物线开口向上,故A、B不符合题意;
当m>0时,则直线y=-mx+n2经过第一、二、四象限,
抛物线y=x2+m 的顶点在y轴的正半轴,故C不符合题意;
当m<0时,则直线y=-mx+n2经过第一、二、三象限,
抛物线y=x2+m 的顶点在y轴的负半轴,故D符合题意;
2.【答案】 C
【解析】解:∵一次函数 的图象经过点 ,每当x增加1个单位时,y增加3个单位,
∴该一次函数图象还经过(3,6),
将点 和(3,6)分别代入 中,得 ,
解得: ,
∴此函数表达式是 ,
3.【答案】 B
【解析】解:如图:
∵∠2=50°,直尺的两边互相平行,
∴∠4=∠2=50°,
∵∠1=30°,
∴∠3=∠4 ∠1=50° 30°=20°.
4.【答案】 B
【解析】∵一次函数y=(2m-3)x-1+m的图象不经过第三象限,
∴ ,
解得1≤m< .
5.【答案】 B
【解析】设当 时,y与x的函数关系式为 ,
,得 ,
即当 时,y与x的函数关系式为 ,
当 时, ,
即小明出发6小时后距A地160千米,
6.【答案】 A
【解析】解:∵点 关于 轴的对称点分别为 ,
∴点A和点P到y轴上任意点的距离都大于AP的长度2,
∴若使 为等腰三角形,AP只能作底,
即点M只能在x轴上,
如图,若AQ为腰, , , , ,共4个;
若AQ为底, ,共1个;
故坐标轴上的点 恰使 、 均为等腰三角形,满足条件的点有5个,
7.【答案】 B
【解析】解:∵
∴DA·BC=20
∵DA=5
∴BC=4
在Rt△BCD中,BC=4,DB=5
∴CD= .
8.【答案】 C
【解析】∵AB∥DE,∴∠B=∠DEC.
∵AC∥DF,∴∠ACB=∠F.(1)∵BE=CF,∴BC=EF.在△ABC和△DEF中,∵∠B=∠DEC,BC=EF,∠ACB=∠F,∴△ABC≌△DEF,故A选项错误;(2)AC=DF,则△ABC和△DEF中,∠ACB=∠F,∠B=∠DEC,AC=DF,∴△ABC≌△DEF,故B选项错误;(3)∠A=∠D,没有边相等,无法证明△ABC≌△DEF;故C选项正确;(4)AB=DE,则△ABC和△DEF中,∵∠B=∠DEC,∠ACB=∠F,AB=DE,∴△ABC≌△DEF,故D选项错误.
9.【答案】 B
【解析】解:先把点(m,n)代入函数y=2x+1,∴2m+1=n,即2m﹣n=﹣1,
∴4m﹣2n+1=2(2m﹣n)+1=2×(﹣1)+1=﹣1.
10.【答案】 C
【解析】解:∵在一次函数y=(2m﹣1)x+1中,y的值随着x值的增大而减小,
∴2m﹣1<0.
∵2m﹣1<0,1>0,
∴一次函数y=(2m﹣1)x+1的图象经过第一、二、四象限,
∴一次函数y=(2m﹣1)x+1的图象不经过第三象限.
二、填空题
11.【答案】 , 或
【解析】解:∵对角线 AC的垂直平分线交AB 于点E,
∴AE=CE,
∵ 长方形OABC中,OA=1,OC=2,
∴AB=OC=2,BC=OA=1,
∴设AE=m,则BE=2-m,CE=m,
∴在Rt BCE中,BE2+ BC2=CE2 , 即:(2-m)2+12=m2 ,
解得:m= ,
∴E(1, ),
设点P坐标为(0,y),
∵△AEP是以为 AE 为腰的等腰三角形,
当AP=AE,则(1-0)2+(0-y)2= (1-1)2+(0- )2 , 解得:y= ,
当EP=AE,则(1-0)2+( -y)2= (1-1)2+(0- )2 , 解得:y= ,
∴点 P的坐标为 , , ,
12.【答案】 x≤5
【解析】根据题意得5﹣x≥0,
所以x≤5.
13.【答案】 15
【解析】 AB=AC,∠BAC=120°, ∠B=∠C=30°, BD=BE,
∠BDE= ,
AD是BC边上的中线,, ∠ADB=90°, ∠ADE=15°.
14.【答案】 ①②③
【解析】在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴∠OBC= ∠ABC,∠OCB= ∠ACB,∠A+∠ABC+∠ACB=180°,
∴∠OBC+∠OCB=90°- ∠A,
∴∠BOC=180°-(∠OBC+∠OCB)=90°,故②∠BOC=90°+ ∠A符合题意;
在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴∠OBC=∠EOB,∠OCB=∠OCF,
∵EF∥BC,
∴∠OBC=∠EOB,∠OCB=∠FOC,
∠EOB=∠OBE,∠FOC=∠OCF,
∴BE=OE,CF=OF,
∴EF=OE+OF=BE+CF,
即①EF=BE+CF符合题意;
过点O作OM⊥AB于M,作ON⊥BC于点N,连接AO,
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴ON=OD=OM=m,即③点O到△ABC各边的距离相等符合题意;
∴S△AEF=S△AOE+ S△AOF= AE·OM+ AF·OD= OD·(AE+AF)= mn,故④不符合题意;
15.【答案】 1
【解析】由原函数是一次函数得,
k+1≠0 且|k|=1
解得:k=1
16.【答案】 (8,1)
【解析】解:延长BC,交y轴于H,过D点作EF⊥x轴于F,交BC于E,
∵反比例函数y= 经过C(2,4),
∴k=2×4=8,
∴y= ,CH=2,OH=4,
设D(m, ),
∴EH=m,DF= ,
∴CE=m﹣2,ED=4﹣ ,
∵四边形OABC是平行四边形,
∴OC∥AB,BC∥OA,
∵CD⊥AB,
∴CD⊥OC,
∴∠OCH+∠ECD=90°,
∵∠OCH+∠HOC=90°,
∴∠HOC=∠ECD,
∵∠OHC=∠CED=90°,
∴△HOC∽△ECD,
∴ ,即 ,
解得,m1=8,m=2(舍去),
∴D(8,1),
17.【答案】 ①③
【解析】解:由图可得,
货车的速度为:300÷5=60千米/小时,故①正确,
设2.5≤x≤4.5时,轿车对应的函数解析式为y=kx+b,
,解得:
∴2.5≤x≤4.5时,轿车对应的函数解析式为y=110x﹣195,
令110x﹣195=60x,得x=3.9,
即轿车与货车相遇时,货车恰好从甲地出发了3.9小时,故②错误,
若轿车到达乙地后,马上沿原路以CD段速度返回,设轿车从乙地出发t小时再次与货车相遇,
则60(4.5+t)+ t=300,得 ,故③正确,
18.【答案】 42°
【解析】解:如图,延长DC交AE于F,
∵AB∥CD,∠BAE=78,
∴∠CFE=78°,
又∵∠DCE=120°,
∴∠E=∠DCE﹣∠CFE=120°﹣78°=42°,
19.【答案】 SSS
【解析】在△ADC和△ABC中,
,
∴△ADC≌△ABC(SSS).
∴∠DAC=∠BAC,
即∠QAE=∠PAE.
20.【答案】
【解析】解:如图,延长AE交DC的延长线于点G . 作 ,交DG于点I . 过点E作 于点H .
根据题意可知 ,
∴ .
∵AE平分 ,
∴ .
∴ ,
∴ ,
∴ ,
∵DE平分 ,
∴ .
∴在 和 中, ,
∴ ,
∴ .
∵ ,
∴ ,
由三角形外角性质可得 ,
∴设 ,则 , .
∵ ,
∴ ,
∴ ,
解得: .
∴ .
在 中, .
∴ .
三、计算题
21.【答案】 解:∵AE⊥BC,∴∠AEB=90°.
∵∠B=60°,
∴∠BAE=90°﹣60°=30°.
∴∠CAE=50°﹣30°=20°
∵∠BAC+∠B+∠ACB=180°,
∴∠ACB=180°﹣∠BAC﹣∠B=70°.
又∵CD平分∠ACB,
∴∠ACD= ∠ACB=35°.
∴∠AFC=180°﹣35°﹣20°=125°.
【解析】先根据垂直的定义求∠BAE的度数,再结合图形根据角的和差求出∠CAE的度数,利用三角形的内角和求∠ACB,因CD平分∠ACB,所以可得∠ACD,最后利用△AFC的内角和为180°,求得∠AFC的度数.
四、作图题
22.【答案】 解:如图所示:
根据三角形具有稳定性.
【解析】根据三角形具有稳定性进行画图即可.
五、解答题
23.【答案】 解:根据题意,可得: , ,
因为在 中, ,
所以 ,
所以 ,
(或利用 与正北方向平行,可得: )
因为 平分 ,
所以 ,
因为 ,
所以 ,
因为在 中, ,
所以 ,
所以 ,
所以 ,
所以 村在 村的南偏东
【解析】在△CAB中,根据三角形内角和定理,可得∠ACB=70°,由角平分线的定义,可得∠ACE=∠ACB=35°,在△CAD中,根据三角形内角和定理,可得∠ACD=25°,利用角的和差关系求出∠DCE的度数即可.
24.【答案】 解:∵△ABC为等边三角形,
∴AB=AC=BC,∠BAC=∠ABC=∠ACB;
又∵∠BAD=∠CBE=∠ACF,
∴∠BAC-∠BAD=∠ABC-∠CBE=∠ACB-∠ACF,
∴∠CAF=∠ABE=∠BCE,
∴△ACF≌△CBE≌△BAD(ASA).
∴AF=BD=CE,AD=BE=CF,
∴AD-AF=BE-BD=CF-CE,
∴DF=DE=EF,
∴△DEF为等边三角形,
∴∠DEF=∠DFE=∠EDF=60°,
又点C点F点E三点共线,
∴∠DEC=120°.
【解析】根据等边三角形的性质和已知条件易证△ACF≌△CBE≌△BAD,再由等边三角形的性质和等边三角形的判定方法易证△DEF为等边三角形,可得∠DEF=60°,根据平角的定义即可求得∠DEC的度数.
25.【答案】 证明:∵AB⊥l于点B,CD⊥l于点D,
∴∠ABE=∠CDF=90°,
∵BF=DE,
∴DF=BE,
∵AE=CF,
∴Rt△ABE≌Rt△CDF(HL),
∴∠AEB=∠CFD,
∴AE∥CF.
【解析】证明△ABE≌△CDF(HL),推出∠AEB=∠CFD可得结论.
数学试题 第3页(共6页) 数学试题 第4页(共6页)
数学答案 第11页(共2页) 数学答案 第12页(共2页)
考试时间:120分钟 满分:120分
姓名:__________ 班级:__________考号:__________
一、单选题(共10题;共30分)
1. ( 3分 ) 在同一坐标系中,一次函数y=一mx+n2与二次函数y=x2+m的图象可能是( )
A. B. C. D.
2. ( 3分 ) 一次函数y=kx+b的图象经过点A(2,3),每当x增加1个单位时,y增加3个单位,则此函数表达式是( )
A. y=3x+3 B. y=2x﹣3 C. y=3x﹣3 D. y=3x﹣2
3. ( 3分 ) 如图,将三角板的直角顶点放在直尺的一边上, , , ( )度
A. 10 B. 20 C. 30 D. 50
4. ( 3分 ) 若一次函数y=(2m﹣3)x﹣1+m的图象不经过第三象限,则m的取值范图是( )
A. 1<m< B. 1≤m< C. 1<m≤ D. 1≤m≤
5. ( 3分 ) 如图,小明从A地前往B地,到达后立刻返回,他与A地的距离 千米 和所用时间 小时 之间的函数关系如图所示,则小明出发6小时后距A地
A. 120千米 B. 160千米 C. 180千米 D. 200千米
6. ( 3分 ) 在平面直角坐标系 中,已知点 关于关于x轴、y轴的对称点分别为P、Q若坐标轴上的点M恰使△MAP、△MAQ均为等腰三角形,则满足条件的M点有( )
A. 5 B. 6 C. 7 D. 9
7. ( 3分 ) 如图,在 中, , 为 上一点,且 ,又 的面积为10,则 的长是( )
A. 2 B. 3 C. 4 D. 5
8. ( 3分 ) 如下图,已知 , ,下列条件中不能判定 ≌ 的是( )
A. B. C. D.
9. ( 3分 ) 若点(m,n)在函数y=2x+1的图象上,则代数式4m﹣2n+1的值是( )
A. 1 B. ﹣1 C. 2 D. ﹣2
10. ( 3分 ) 在一次函数y=(2m﹣1)x+1中,y的值随着x值的增大而减小,则它的图象不经过( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
二、填空题(共10题;共20分)
11. ( 2分 ) 如图,在平面直角坐标系中,长方形OABC的边OA 在x轴上,OC在y轴上,OA=1,OC=2,对角线 AC的垂直平分线交AB 于点E,交AC于点D.若y轴上有一点P(不与点C重合),能使△AEP是以为 AE 为腰的等腰三角形,则点 P的坐标为 .
12. ( 2分 ) 若函数y= 在实数范围内有意义,则自变量x的取值范围是 .
13. ( 2分 ) 如图,△ABC中,AB=AC,∠BAC=124°,AD是BC边上的中线,且BD=BE,则∠ADE是________度.
14. ( 2分 ) 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O , 过点O作EF∥BC交AB于E , 交AC于F , 过点O作OD⊥AC于D , 下列四个结论:
①EF=BE+CF;
②∠BOC=90°+ ∠A;
③点O到△ABC各边的距离相等;
④设OD=m , AE+AF=n , 则 .
其中正确的结论是________.(填序号)
15. ( 2分 ) 若y=(k+1)x|k|+m+4是一次函数,则k=________.
16. ( 2分 ) 如图,在平面直角坐标系中, OABC的顶点A在x轴的正半轴上,C为(2,4),CD⊥AB于点D,反比例函数y= 恰好经过点C,D,则点D的坐标为 .
17. ( 2分 ) 甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地.如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系式;折线B﹣C﹣D表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.
下面几种说法:①货车的速度为60千米/小时;
②轿车与货车相遇时,货车恰好从甲地出发了3小时;
③若轿车到达乙地后,马上沿原路以CD段速度返回,则轿车从乙地出发 小时再次与货车相遇;其中正确的是________.(填写序号)
18. ( 2分 ) 某同学在研究传统文化“抖空竹”时有一个发现:他把它抽象成数学问题.如图所示,已知AB∥CD,∠BAE=78°,∠DCE=120°,则∠E的度数是________.
19. ( 2分 ) 如图,小敏做了一个角平分仪ABCD,其中 , ,将仪器上的点A与 的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是 的平分线 此角平分仪的画图原理是:根据仪器结构,可得 ≌ ,这样就有 则说明这两个三角形全等的依据是
20. ( 2分 ) 如图,在 ABCD中,AD=6,对角线BD⊥CD , ∠BAD=30°,∠BAD与∠CDB的平分线交于点E , 延长DB到点F , 使DF=AD , 连接EF , 则EF的长为 .
三、计算题(共1题;共10分)
21. ( 10分 ) 如图,在△ABC中,∠BAC=50°,∠B=60°,AE⊥BC于点E,CD平分∠ACB且分别与AB、AE交于点D、F,求∠AFC的度数.
四、作图题(共1题;共10分)
22. ( 10分 ) 小辉用7根木条钉成一个七边形的木架,他为了使该木架稳固,想在其中加上四根木条,请你在图1、2、3中画出你的三种想法,并说明加上木条后使该木架稳固所用的数学道理
五、解答题(共3题;共50分)
23. ( 15分 ) 如图, 村在 村的正东方, 村在 村的北偏东 方向,且在 村的西北方, ,垂足为点 , 村在 上,连接 ,恰好平分 ,那么 村在 村的什么方向?
24. ( 15分 ) 如图,△ABC为等边三角形,∠BAD=∠ACF=∠CBE,求∠DEC的度数。
25. ( 20分 ) 如图AB⊥l于点B , CD⊥l于点D , 点E , F在直线1上,且BF=DE , AE=CF . 求证:AE∥CF .
数学试题 第3页(共4页) 数学试题 第4页(共4页)
数学试题 第1页(共6页) 数学试题 第2页(共6页)
答案解析部分
一、单选题
1.【答案】 D
【解析】解:∵ 一次函数y=-mx+n2 , 抛物线y=x2+m
n2>0,
∴此函数与y轴交于正半轴,且抛物线开口向上,故A、B不符合题意;
当m>0时,则直线y=-mx+n2经过第一、二、四象限,
抛物线y=x2+m 的顶点在y轴的正半轴,故C不符合题意;
当m<0时,则直线y=-mx+n2经过第一、二、三象限,
抛物线y=x2+m 的顶点在y轴的负半轴,故D符合题意;
2.【答案】 C
【解析】解:∵一次函数 的图象经过点 ,每当x增加1个单位时,y增加3个单位,
∴该一次函数图象还经过(3,6),
将点 和(3,6)分别代入 中,得 ,
解得: ,
∴此函数表达式是 ,
3.【答案】 B
【解析】解:如图:
∵∠2=50°,直尺的两边互相平行,
∴∠4=∠2=50°,
∵∠1=30°,
∴∠3=∠4 ∠1=50° 30°=20°.
4.【答案】 B
【解析】∵一次函数y=(2m-3)x-1+m的图象不经过第三象限,
∴ ,
解得1≤m< .
5.【答案】 B
【解析】设当 时,y与x的函数关系式为 ,
,得 ,
即当 时,y与x的函数关系式为 ,
当 时, ,
即小明出发6小时后距A地160千米,
6.【答案】 A
【解析】解:∵点 关于 轴的对称点分别为 ,
∴点A和点P到y轴上任意点的距离都大于AP的长度2,
∴若使 为等腰三角形,AP只能作底,
即点M只能在x轴上,
如图,若AQ为腰, , , , ,共4个;
若AQ为底, ,共1个;
故坐标轴上的点 恰使 、 均为等腰三角形,满足条件的点有5个,
7.【答案】 B
【解析】解:∵
∴DA·BC=20
∵DA=5
∴BC=4
在Rt△BCD中,BC=4,DB=5
∴CD= .
8.【答案】 C
【解析】∵AB∥DE,∴∠B=∠DEC.
∵AC∥DF,∴∠ACB=∠F.(1)∵BE=CF,∴BC=EF.在△ABC和△DEF中,∵∠B=∠DEC,BC=EF,∠ACB=∠F,∴△ABC≌△DEF,故A选项错误;(2)AC=DF,则△ABC和△DEF中,∠ACB=∠F,∠B=∠DEC,AC=DF,∴△ABC≌△DEF,故B选项错误;(3)∠A=∠D,没有边相等,无法证明△ABC≌△DEF;故C选项正确;(4)AB=DE,则△ABC和△DEF中,∵∠B=∠DEC,∠ACB=∠F,AB=DE,∴△ABC≌△DEF,故D选项错误.
9.【答案】 B
【解析】解:先把点(m,n)代入函数y=2x+1,∴2m+1=n,即2m﹣n=﹣1,
∴4m﹣2n+1=2(2m﹣n)+1=2×(﹣1)+1=﹣1.
10.【答案】 C
【解析】解:∵在一次函数y=(2m﹣1)x+1中,y的值随着x值的增大而减小,
∴2m﹣1<0.
∵2m﹣1<0,1>0,
∴一次函数y=(2m﹣1)x+1的图象经过第一、二、四象限,
∴一次函数y=(2m﹣1)x+1的图象不经过第三象限.
二、填空题
11.【答案】 , 或
【解析】解:∵对角线 AC的垂直平分线交AB 于点E,
∴AE=CE,
∵ 长方形OABC中,OA=1,OC=2,
∴AB=OC=2,BC=OA=1,
∴设AE=m,则BE=2-m,CE=m,
∴在Rt BCE中,BE2+ BC2=CE2 , 即:(2-m)2+12=m2 ,
解得:m= ,
∴E(1, ),
设点P坐标为(0,y),
∵△AEP是以为 AE 为腰的等腰三角形,
当AP=AE,则(1-0)2+(0-y)2= (1-1)2+(0- )2 , 解得:y= ,
当EP=AE,则(1-0)2+( -y)2= (1-1)2+(0- )2 , 解得:y= ,
∴点 P的坐标为 , , ,
12.【答案】 x≤5
【解析】根据题意得5﹣x≥0,
所以x≤5.
13.【答案】 15
【解析】 AB=AC,∠BAC=120°, ∠B=∠C=30°, BD=BE,
∠BDE= ,
AD是BC边上的中线,, ∠ADB=90°, ∠ADE=15°.
14.【答案】 ①②③
【解析】在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴∠OBC= ∠ABC,∠OCB= ∠ACB,∠A+∠ABC+∠ACB=180°,
∴∠OBC+∠OCB=90°- ∠A,
∴∠BOC=180°-(∠OBC+∠OCB)=90°,故②∠BOC=90°+ ∠A符合题意;
在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴∠OBC=∠EOB,∠OCB=∠OCF,
∵EF∥BC,
∴∠OBC=∠EOB,∠OCB=∠FOC,
∠EOB=∠OBE,∠FOC=∠OCF,
∴BE=OE,CF=OF,
∴EF=OE+OF=BE+CF,
即①EF=BE+CF符合题意;
过点O作OM⊥AB于M,作ON⊥BC于点N,连接AO,
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴ON=OD=OM=m,即③点O到△ABC各边的距离相等符合题意;
∴S△AEF=S△AOE+ S△AOF= AE·OM+ AF·OD= OD·(AE+AF)= mn,故④不符合题意;
15.【答案】 1
【解析】由原函数是一次函数得,
k+1≠0 且|k|=1
解得:k=1
16.【答案】 (8,1)
【解析】解:延长BC,交y轴于H,过D点作EF⊥x轴于F,交BC于E,
∵反比例函数y= 经过C(2,4),
∴k=2×4=8,
∴y= ,CH=2,OH=4,
设D(m, ),
∴EH=m,DF= ,
∴CE=m﹣2,ED=4﹣ ,
∵四边形OABC是平行四边形,
∴OC∥AB,BC∥OA,
∵CD⊥AB,
∴CD⊥OC,
∴∠OCH+∠ECD=90°,
∵∠OCH+∠HOC=90°,
∴∠HOC=∠ECD,
∵∠OHC=∠CED=90°,
∴△HOC∽△ECD,
∴ ,即 ,
解得,m1=8,m=2(舍去),
∴D(8,1),
17.【答案】 ①③
【解析】解:由图可得,
货车的速度为:300÷5=60千米/小时,故①正确,
设2.5≤x≤4.5时,轿车对应的函数解析式为y=kx+b,
,解得:
∴2.5≤x≤4.5时,轿车对应的函数解析式为y=110x﹣195,
令110x﹣195=60x,得x=3.9,
即轿车与货车相遇时,货车恰好从甲地出发了3.9小时,故②错误,
若轿车到达乙地后,马上沿原路以CD段速度返回,设轿车从乙地出发t小时再次与货车相遇,
则60(4.5+t)+ t=300,得 ,故③正确,
18.【答案】 42°
【解析】解:如图,延长DC交AE于F,
∵AB∥CD,∠BAE=78,
∴∠CFE=78°,
又∵∠DCE=120°,
∴∠E=∠DCE﹣∠CFE=120°﹣78°=42°,
19.【答案】 SSS
【解析】在△ADC和△ABC中,
,
∴△ADC≌△ABC(SSS).
∴∠DAC=∠BAC,
即∠QAE=∠PAE.
20.【答案】
【解析】解:如图,延长AE交DC的延长线于点G . 作 ,交DG于点I . 过点E作 于点H .
根据题意可知 ,
∴ .
∵AE平分 ,
∴ .
∴ ,
∴ ,
∴ ,
∵DE平分 ,
∴ .
∴在 和 中, ,
∴ ,
∴ .
∵ ,
∴ ,
由三角形外角性质可得 ,
∴设 ,则 , .
∵ ,
∴ ,
∴ ,
解得: .
∴ .
在 中, .
∴ .
三、计算题
21.【答案】 解:∵AE⊥BC,∴∠AEB=90°.
∵∠B=60°,
∴∠BAE=90°﹣60°=30°.
∴∠CAE=50°﹣30°=20°
∵∠BAC+∠B+∠ACB=180°,
∴∠ACB=180°﹣∠BAC﹣∠B=70°.
又∵CD平分∠ACB,
∴∠ACD= ∠ACB=35°.
∴∠AFC=180°﹣35°﹣20°=125°.
【解析】先根据垂直的定义求∠BAE的度数,再结合图形根据角的和差求出∠CAE的度数,利用三角形的内角和求∠ACB,因CD平分∠ACB,所以可得∠ACD,最后利用△AFC的内角和为180°,求得∠AFC的度数.
四、作图题
22.【答案】 解:如图所示:
根据三角形具有稳定性.
【解析】根据三角形具有稳定性进行画图即可.
五、解答题
23.【答案】 解:根据题意,可得: , ,
因为在 中, ,
所以 ,
所以 ,
(或利用 与正北方向平行,可得: )
因为 平分 ,
所以 ,
因为 ,
所以 ,
因为在 中, ,
所以 ,
所以 ,
所以 ,
所以 村在 村的南偏东
【解析】在△CAB中,根据三角形内角和定理,可得∠ACB=70°,由角平分线的定义,可得∠ACE=∠ACB=35°,在△CAD中,根据三角形内角和定理,可得∠ACD=25°,利用角的和差关系求出∠DCE的度数即可.
24.【答案】 解:∵△ABC为等边三角形,
∴AB=AC=BC,∠BAC=∠ABC=∠ACB;
又∵∠BAD=∠CBE=∠ACF,
∴∠BAC-∠BAD=∠ABC-∠CBE=∠ACB-∠ACF,
∴∠CAF=∠ABE=∠BCE,
∴△ACF≌△CBE≌△BAD(ASA).
∴AF=BD=CE,AD=BE=CF,
∴AD-AF=BE-BD=CF-CE,
∴DF=DE=EF,
∴△DEF为等边三角形,
∴∠DEF=∠DFE=∠EDF=60°,
又点C点F点E三点共线,
∴∠DEC=120°.
【解析】根据等边三角形的性质和已知条件易证△ACF≌△CBE≌△BAD,再由等边三角形的性质和等边三角形的判定方法易证△DEF为等边三角形,可得∠DEF=60°,根据平角的定义即可求得∠DEC的度数.
25.【答案】 证明:∵AB⊥l于点B,CD⊥l于点D,
∴∠ABE=∠CDF=90°,
∵BF=DE,
∴DF=BE,
∵AE=CF,
∴Rt△ABE≌Rt△CDF(HL),
∴∠AEB=∠CFD,
∴AE∥CF.
【解析】证明△ABE≌△CDF(HL),推出∠AEB=∠CFD可得结论.
数学试题 第3页(共6页) 数学试题 第4页(共6页)
数学答案 第11页(共2页) 数学答案 第12页(共2页)
