2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册2.3.2两点间的距离公式课件(共11张PPT)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册2.3.2两点间的距离公式课件(共11张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 314.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-08 11:10:32 | ||
图片预览




文档简介
(共11张PPT)
2.3.2 两点间的距离
我们知道,在各种几何量中,直线段的长度是最基本的. 所以,在解析几何中,最基本的公式自然是用平面内两点的坐标表示这两点间距离的公式.
探究 如图, 已知平面内两点P1(x1, y1), P2(x2, y2), 如何求P1, P2间的距离| P1P2 |
O
y
x
P1(x1,y1)
P2(x2,y2)
我们用平面向量的知识来解决. 如图, 由点P1(x1, y1), P2(x2, y2), 得 于是
由此得到P1(x1, y1), P2(x2, y2)两点间的距离公式为
特别地, 原点O(0, 0)与任一点P(x, y)间的距离为
思考 你还有其它推导两点间的距离公式的方法吗?
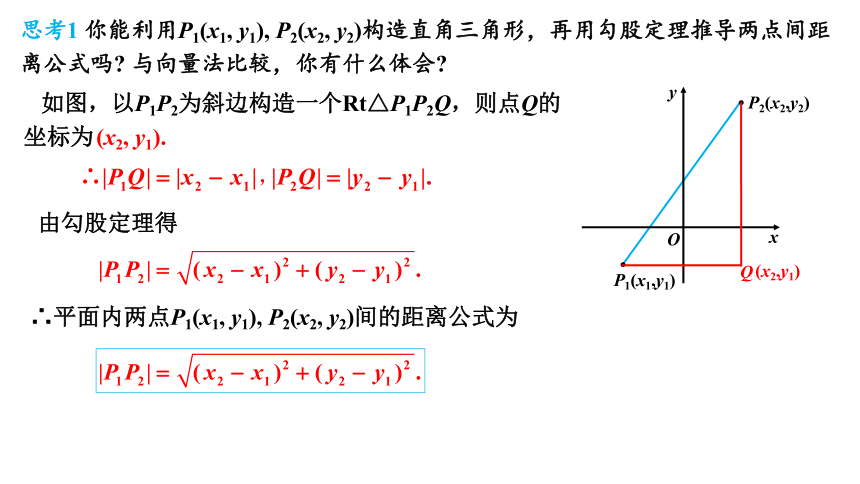
如图,以P1P2为斜边构造一个Rt△P1P2Q,则点Q的坐标为
思考1 你能利用P1(x1, y1), P2(x2, y2)构造直角三角形,再用勾股定理推导两点间距离公式吗 与向量法比较,你有什么体会
O
y
x
P1(x1,y1)
P2(x2,y2)
Q
(x2,y1)
(x2, y1).
由勾股定理得
∴平面内两点P1(x1, y1), P2(x2, y2)间的距离公式为
1. 求下列两点间的距离:
(1) A(6, 0), B(-2, 0);
(2) C(0, -4), D(0, C1);
(3) P(6, 0), Q(0, -2);
(4) M(2, 1), N(5, -1).
|AB|=8
|CD|=3
2. 已知A(a, -5)与B(0, 10)两点间的距离是17,求a的值.
例3 已知点A(-1, 2), B(2, ), 在x轴上求一点P, 使得|PA|=|PB|, 并求|PA|的值.
巩固训练1 求在x轴上与点A(5,12)的距离为13的的点的坐标.
巩固训练2 已知点P的横坐标是7, 点P与点N(-1,5)间的距离等于10,求点P的纵坐标.
例4 用坐标法证明: 平行四边形两条对角线的平方和等于两条相邻的平方和的两倍.
y
x
O
(a+b,c)
A
B
D
C
(b,c)
(0,0)
(a,0)
证明: 如图示, 四边形ABCD是平行四边形, 以顶点A为原点, 边AB所在直线为x轴, 建立平面直角坐标系.
在 ABCD中, 点A的坐标是(0, 0), 设点B的坐标为(a,0), 点D的坐标为(b,c), 由平行四边形的性质, 得点C的坐标为(a+b,c).
即平行四边形两条对角线的平方和等于两条相邻的平方和的两倍.
第一步:建立坐标系,用坐标表示有关的量;
第二步:进行有关的代数运算;
第三步:把代数运算结果“翻译”成几何关系.
思考2 在“平面向量及其应用”的学习中,我们用“向量法”证明过这个命题. 你能回忆一下证明过程吗 比较“坐标法”和“向量法”,你有什么体会
用坐标法证明简单的平面几何问题的步骤:
思考3 根据例4的条件,你是否还有其他建立坐标系的方法 你能说说建立适当坐标系对证明的重要性吗
还有其他建立坐标系的方法,如AB的中点为原点,AB所在直线为x轴建立坐标系,或以两条对角线交点为原点,与AB平行的直线为x轴建立坐标系等.
坐标系的建立是否适当,对证明非常重要,如若不然,点的坐标会比较复杂,从而加大计算量,增加出错的几率.
y
x
O
B
C
A
M
(0,0)
(a,0)
(0,b)
3. 用坐标法证明:直角三角形斜边的中点到三个顶点的距离相等.
即直角三角形斜边的中点到三个顶点的距离相等.
2.用坐标法(解析法)解决几何问题的基本步骤
第一步:建立适当的直角坐标系,用坐标表示有关的量;
第二步:进行有关的代数计算;
第三步:把代数运算结果“翻译”成几何关系.
[注意] 建系时让图形中尽可能多的点落在坐标轴上,这样便于运算.
小结:
1.平面内两点P1(x1, y1), P2(x2, y2)间的距离公式为
课后作业:
课后达标检测P113-114第3,6,10,11,12,13,课本P79习题2.3第3,4,5
2.3.2 两点间的距离
我们知道,在各种几何量中,直线段的长度是最基本的. 所以,在解析几何中,最基本的公式自然是用平面内两点的坐标表示这两点间距离的公式.
探究 如图, 已知平面内两点P1(x1, y1), P2(x2, y2), 如何求P1, P2间的距离| P1P2 |
O
y
x
P1(x1,y1)
P2(x2,y2)
我们用平面向量的知识来解决. 如图, 由点P1(x1, y1), P2(x2, y2), 得 于是
由此得到P1(x1, y1), P2(x2, y2)两点间的距离公式为
特别地, 原点O(0, 0)与任一点P(x, y)间的距离为
思考 你还有其它推导两点间的距离公式的方法吗?
如图,以P1P2为斜边构造一个Rt△P1P2Q,则点Q的坐标为
思考1 你能利用P1(x1, y1), P2(x2, y2)构造直角三角形,再用勾股定理推导两点间距离公式吗 与向量法比较,你有什么体会
O
y
x
P1(x1,y1)
P2(x2,y2)
Q
(x2,y1)
(x2, y1).
由勾股定理得
∴平面内两点P1(x1, y1), P2(x2, y2)间的距离公式为
1. 求下列两点间的距离:
(1) A(6, 0), B(-2, 0);
(2) C(0, -4), D(0, C1);
(3) P(6, 0), Q(0, -2);
(4) M(2, 1), N(5, -1).
|AB|=8
|CD|=3
2. 已知A(a, -5)与B(0, 10)两点间的距离是17,求a的值.
例3 已知点A(-1, 2), B(2, ), 在x轴上求一点P, 使得|PA|=|PB|, 并求|PA|的值.
巩固训练1 求在x轴上与点A(5,12)的距离为13的的点的坐标.
巩固训练2 已知点P的横坐标是7, 点P与点N(-1,5)间的距离等于10,求点P的纵坐标.
例4 用坐标法证明: 平行四边形两条对角线的平方和等于两条相邻的平方和的两倍.
y
x
O
(a+b,c)
A
B
D
C
(b,c)
(0,0)
(a,0)
证明: 如图示, 四边形ABCD是平行四边形, 以顶点A为原点, 边AB所在直线为x轴, 建立平面直角坐标系.
在 ABCD中, 点A的坐标是(0, 0), 设点B的坐标为(a,0), 点D的坐标为(b,c), 由平行四边形的性质, 得点C的坐标为(a+b,c).
即平行四边形两条对角线的平方和等于两条相邻的平方和的两倍.
第一步:建立坐标系,用坐标表示有关的量;
第二步:进行有关的代数运算;
第三步:把代数运算结果“翻译”成几何关系.
思考2 在“平面向量及其应用”的学习中,我们用“向量法”证明过这个命题. 你能回忆一下证明过程吗 比较“坐标法”和“向量法”,你有什么体会
用坐标法证明简单的平面几何问题的步骤:
思考3 根据例4的条件,你是否还有其他建立坐标系的方法 你能说说建立适当坐标系对证明的重要性吗
还有其他建立坐标系的方法,如AB的中点为原点,AB所在直线为x轴建立坐标系,或以两条对角线交点为原点,与AB平行的直线为x轴建立坐标系等.
坐标系的建立是否适当,对证明非常重要,如若不然,点的坐标会比较复杂,从而加大计算量,增加出错的几率.
y
x
O
B
C
A
M
(0,0)
(a,0)
(0,b)
3. 用坐标法证明:直角三角形斜边的中点到三个顶点的距离相等.
即直角三角形斜边的中点到三个顶点的距离相等.
2.用坐标法(解析法)解决几何问题的基本步骤
第一步:建立适当的直角坐标系,用坐标表示有关的量;
第二步:进行有关的代数计算;
第三步:把代数运算结果“翻译”成几何关系.
[注意] 建系时让图形中尽可能多的点落在坐标轴上,这样便于运算.
小结:
1.平面内两点P1(x1, y1), P2(x2, y2)间的距离公式为
课后作业:
课后达标检测P113-114第3,6,10,11,12,13,课本P79习题2.3第3,4,5
