2021-2022学年高一上学期数学人教A版(2019)必修第一册5.4.1-5.4.2正弦函数、余弦函数的图象与性质题型训练
文档属性
| 名称 | 2021-2022学年高一上学期数学人教A版(2019)必修第一册5.4.1-5.4.2正弦函数、余弦函数的图象与性质题型训练 | 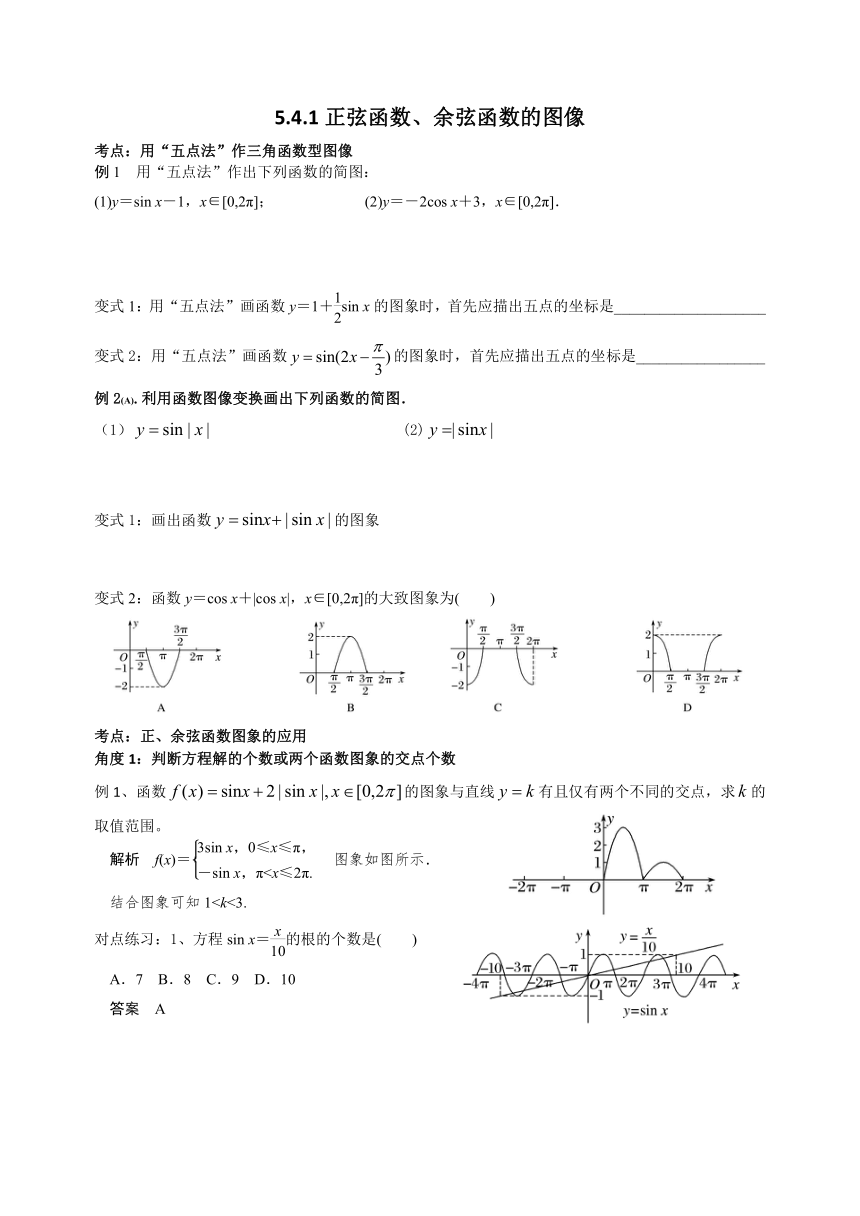 | |
| 格式 | docx | ||
| 文件大小 | 279.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-08 15:52:16 | ||
图片预览




文档简介
5.4.1正弦函数、余弦函数的图像
考点:用“五点法”作三角函数型图像
例1 用“五点法”作出下列函数的简图:
(1)y=sin x-1,x∈[0,2π]; (2)y=-2cos x+3,x∈[0,2π].
变式1:用“五点法”画函数y=1+sin x的图象时,首先应描出五点的坐标是____________________
变式2:用“五点法”画函数的图象时,首先应描出五点的坐标是_________________
例2(A).利用函数图像变换画出下列函数的简图.
(1) (2)
变式1:画出函数的图象
变式2:函数y=cos x+|cos x|,x∈[0,2π]的大致图象为( )
考点:正、余弦函数图象的应用
角度1:判断方程解的个数或两个函数图象的交点个数
例1、函数的图象与直线有且仅有两个不同的交点,求的取值范围。
解析 f(x)=图象如图所示.
结合图象可知1对点练习:1、方程sin x=的根的个数是( )
A.7 B.8 C.9 D.10
答案 A
2、若方程sin x=在上有两个实数根,求a的取值范围.
由图象可知,当≤<1,即-13、求方程的实数根的个数为_________
角度2:解三角函数的方程问题
例1、解方程
变式:解方程
角度3:解三角函数的不等式问题
例1、不等式2sin x-1≥0,x∈[0,2π]解集为______________
变式1:不等式2sin x-1≥0的解集为_____________
变式2:解不等式
变式3:解不等式的解集
变式4:解不等式的解集
5.4.2正弦函数、余弦函数的性质
函数 y=sin t y=cos t
图像
定义域
值域
对称性 对称轴:______________ 对称中心:_____________ 对称轴:______________ 对称中心:_____________
奇偶性
周期性 最小正周期: 最小正周期:
单调性 递增区间______________ 递减区间______________ 递增区间______________ 递减区间______________
最值 当t= _ __时,ymax=1 当t= 时,ymin=-1 当t= _ __时,ymax=1 当t= 时,ymin=-1
题型一:正、余弦型函数的周期的求法和应用
例1、函数的最小正周期为_______
法一:定义法
法二:公式法
法三:图像法
变式:函数的最小正周期为_______
练习:
1、求下列函数的最小正周期
2、设,则f(1)+f(2)+f(3)+…+f(2021)等于 ________
3、设f(x)是定义域为R,最小正周期为的函数,当-≤x<π时,f(x)=则______
4、已知函数的周期为,则_______
5、已知直线y=b(00)的图像在y轴右侧的三个相邻交点的横坐标依次为x1=,x2=,x3=,则ω的值为 .
6、已知函数在区间上至少出现10次最大值,则的最小值是_______
题型二:正、余弦型函数的奇偶性和对称性
例1、判断下列函数的奇偶性
变式1:判断下列函数的奇偶性,其中x∈R.
(1)f(x)=+x2sin x;
(2)f(x)=lg(1-sin x)-lg(1+sin x)
(3)f(x)=+
(4)f(x)=sin(cos x).
变式2 :函数是 ( )
A.最小正周期为π的奇函数 B.最小正周期为π的偶函数
C.最小正周期为2π的奇函数 D.最小正周期为2π的偶函数
变式3:若函数y=sin(ωx+φ)是奇函数,则φ=________
变式4:若函数y=sin(ωx+φ)是偶函数,则φ=________
变式5:若函数y=cos(ωx+φ)是偶函数,则φ=________
变式6:若函数y=cos(ωx+φ)是奇函数,则φ=________
对点练习:已知函数是偶函数,则=____
例2、函数的对称轴是____________对称中心是___________
变式1:函数的对称轴是____________对称中心是___________
变式2:若直线x=a是函数图像的一条对称轴,则a的值可能是 ( )
A. B. C.- D.-
变式3:已知函数的图像关于直线对称,则=____
变式4:已知函数的图像关于点对称,则=____
题型三:正、余弦型函数单调区间的求法及单调性的应用
角度1:求正、余弦型函数的单调区间
例1、求函数的单调区间.
变式1:求的单调区间.
变式2:求函数的单调递增区间
变式3:求函数单调递减区间
变式4:求函数单调递增区间
变式5:求函数的单调递增区间
变式6:下列函数中周期为,且在上为递增函数的是( )
A. B. C. D.
角度2:已知正、余弦型函数的单调性求参数范围
例2、已知,函数在区间上单调递增,则的取值范围是________
对点练习1:函数在上单调递减,则的取值范围是( )
A. B. C. D.
练习2、设且,则使函数在区间上不单调的的个数是___________.
角度3:利用正余弦函数的单调性比大小
例3、比较下列各组数的大小:
(1)与 (2)与 (3)
练习1、比较下列两组数的大小:
(1)与 (2)与
练习2、设,则下列不等式正确的是( )
A. B. C. D.
题型四:求正余弦型函数的值域
角度1:利用三角函数的单调性求值域
例1、已知,求函数的值域
变式1:已知,求函数的值域
变式2:求函数() 的值域
变式3:求函数的值域
变式4:求函数的值域
变式5:函数在区间上的最大值是___________
变式6:设函数,其中,为实常数,,已知函数的值域是,求,的值.
变式7:若函数y=asin(2x)+b ,的最大值为3,最小值为-1,求a, b
变式8:若关于x的方程在区间上有两个不同的根,求m的取值范围。
变式9:已知函数,其中,若对恒成立,且,求的表达式与单调递减区间.
角度2:利用三角函数的有界性求值域
例2、求函数的值域
变式:求函数的值域
角度3:可化为型,此类型通常用换元法:可设,化为关于的二次函数,再根据定义域求值域
例3、求函数的值域
变式1:求函数的值域
变式2:求函数的最大值
变式3:当函数的最大值为1时,求a的值
变式4:已知,求的最大值和最小值.
题型五:求正余弦型函数的最值
例5、求下列函数的值域及取得最大值时自变量的集合:
(1) (2) (3)
题型六:已知三角函数的性质求参数
1、若函数图像的一条对称轴是直线,则的最小值是__________
2、函数相邻两对称轴之间的距离为2,则=_____
3、已知函数(其中,)的图象在上恰有四个对称中心,则的取值范围是______________________.
考点:用“五点法”作三角函数型图像
例1 用“五点法”作出下列函数的简图:
(1)y=sin x-1,x∈[0,2π]; (2)y=-2cos x+3,x∈[0,2π].
变式1:用“五点法”画函数y=1+sin x的图象时,首先应描出五点的坐标是____________________
变式2:用“五点法”画函数的图象时,首先应描出五点的坐标是_________________
例2(A).利用函数图像变换画出下列函数的简图.
(1) (2)
变式1:画出函数的图象
变式2:函数y=cos x+|cos x|,x∈[0,2π]的大致图象为( )
考点:正、余弦函数图象的应用
角度1:判断方程解的个数或两个函数图象的交点个数
例1、函数的图象与直线有且仅有两个不同的交点,求的取值范围。
解析 f(x)=图象如图所示.
结合图象可知1
A.7 B.8 C.9 D.10
答案 A
2、若方程sin x=在上有两个实数根,求a的取值范围.
由图象可知,当≤<1,即-1
角度2:解三角函数的方程问题
例1、解方程
变式:解方程
角度3:解三角函数的不等式问题
例1、不等式2sin x-1≥0,x∈[0,2π]解集为______________
变式1:不等式2sin x-1≥0的解集为_____________
变式2:解不等式
变式3:解不等式的解集
变式4:解不等式的解集
5.4.2正弦函数、余弦函数的性质
函数 y=sin t y=cos t
图像
定义域
值域
对称性 对称轴:______________ 对称中心:_____________ 对称轴:______________ 对称中心:_____________
奇偶性
周期性 最小正周期: 最小正周期:
单调性 递增区间______________ 递减区间______________ 递增区间______________ 递减区间______________
最值 当t= _ __时,ymax=1 当t= 时,ymin=-1 当t= _ __时,ymax=1 当t= 时,ymin=-1
题型一:正、余弦型函数的周期的求法和应用
例1、函数的最小正周期为_______
法一:定义法
法二:公式法
法三:图像法
变式:函数的最小正周期为_______
练习:
1、求下列函数的最小正周期
2、设,则f(1)+f(2)+f(3)+…+f(2021)等于 ________
3、设f(x)是定义域为R,最小正周期为的函数,当-≤x<π时,f(x)=则______
4、已知函数的周期为,则_______
5、已知直线y=b(0
6、已知函数在区间上至少出现10次最大值,则的最小值是_______
题型二:正、余弦型函数的奇偶性和对称性
例1、判断下列函数的奇偶性
变式1:判断下列函数的奇偶性,其中x∈R.
(1)f(x)=+x2sin x;
(2)f(x)=lg(1-sin x)-lg(1+sin x)
(3)f(x)=+
(4)f(x)=sin(cos x).
变式2 :函数是 ( )
A.最小正周期为π的奇函数 B.最小正周期为π的偶函数
C.最小正周期为2π的奇函数 D.最小正周期为2π的偶函数
变式3:若函数y=sin(ωx+φ)是奇函数,则φ=________
变式4:若函数y=sin(ωx+φ)是偶函数,则φ=________
变式5:若函数y=cos(ωx+φ)是偶函数,则φ=________
变式6:若函数y=cos(ωx+φ)是奇函数,则φ=________
对点练习:已知函数是偶函数,则=____
例2、函数的对称轴是____________对称中心是___________
变式1:函数的对称轴是____________对称中心是___________
变式2:若直线x=a是函数图像的一条对称轴,则a的值可能是 ( )
A. B. C.- D.-
变式3:已知函数的图像关于直线对称,则=____
变式4:已知函数的图像关于点对称,则=____
题型三:正、余弦型函数单调区间的求法及单调性的应用
角度1:求正、余弦型函数的单调区间
例1、求函数的单调区间.
变式1:求的单调区间.
变式2:求函数的单调递增区间
变式3:求函数单调递减区间
变式4:求函数单调递增区间
变式5:求函数的单调递增区间
变式6:下列函数中周期为,且在上为递增函数的是( )
A. B. C. D.
角度2:已知正、余弦型函数的单调性求参数范围
例2、已知,函数在区间上单调递增,则的取值范围是________
对点练习1:函数在上单调递减,则的取值范围是( )
A. B. C. D.
练习2、设且,则使函数在区间上不单调的的个数是___________.
角度3:利用正余弦函数的单调性比大小
例3、比较下列各组数的大小:
(1)与 (2)与 (3)
练习1、比较下列两组数的大小:
(1)与 (2)与
练习2、设,则下列不等式正确的是( )
A. B. C. D.
题型四:求正余弦型函数的值域
角度1:利用三角函数的单调性求值域
例1、已知,求函数的值域
变式1:已知,求函数的值域
变式2:求函数() 的值域
变式3:求函数的值域
变式4:求函数的值域
变式5:函数在区间上的最大值是___________
变式6:设函数,其中,为实常数,,已知函数的值域是,求,的值.
变式7:若函数y=asin(2x)+b ,的最大值为3,最小值为-1,求a, b
变式8:若关于x的方程在区间上有两个不同的根,求m的取值范围。
变式9:已知函数,其中,若对恒成立,且,求的表达式与单调递减区间.
角度2:利用三角函数的有界性求值域
例2、求函数的值域
变式:求函数的值域
角度3:可化为型,此类型通常用换元法:可设,化为关于的二次函数,再根据定义域求值域
例3、求函数的值域
变式1:求函数的值域
变式2:求函数的最大值
变式3:当函数的最大值为1时,求a的值
变式4:已知,求的最大值和最小值.
题型五:求正余弦型函数的最值
例5、求下列函数的值域及取得最大值时自变量的集合:
(1) (2) (3)
题型六:已知三角函数的性质求参数
1、若函数图像的一条对称轴是直线,则的最小值是__________
2、函数相邻两对称轴之间的距离为2,则=_____
3、已知函数(其中,)的图象在上恰有四个对称中心,则的取值范围是______________________.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
