7.2.2 定理与证明 课件(共20张PPT)
文档属性
| 名称 | 7.2.2 定理与证明 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 09:56:23 | ||
图片预览








文档简介
(共20张PPT)
北师版八年级上册 平行线的证明
§7.2.2 定理与证明
1.理解公理和定理的意义,并能对公理与定理加以区别.
2.理解证明命题的思路、书写的格式,使学生对几何的重要内容之一——
推理论证,有初步的认识,从而培养思维的条理性和逻辑性.(重点)
知点
用我们以前学过的观察、实验、验证特例等方法.
这些方法往往不可靠.
能不能根据已经知道的真命题证实呢?
情境导入
那已经知道的真命题又是如何证实的?
哦……那可怎么办?
情境导入
其实,在数学发展史上,数学家们也遇到过类似的问题.公元前3世纪,人们已经积累了大量的数学知识,在此基础上,古希腊数学家欧几里得 (Euclid,公元前300年前后)编写了一本书,书名叫做《原本》(Elements). 为了说明每一结论的正确性,他在编写这本书时进行了大胆创造:挑选了一部分数
学名词和一部分公认的真命题作为证实其他命题的出发点和依据,其中的数学名词称为原名,公认的真命题称为公理(axiom).除了公理外,其他命题的真假都需要通过演绎推理的方法进行判断.
新知讲解
(1)两点确定一条直线.
(2)两点之间线段最短.
(3)同一平面内,过一点有且只有一条直线与已知直线垂直.
(4)两条直线被第三条直线所截,如果同位角相等,那么这两
条直线平行 (简述为:同位角相等,两直线平行).
(5)过直线外一点有且只有一条直线与这条直线平行.
(6)两边及其夹角分别相等的两个三角形全等.
新知讲解
(7)两角及其夹边分别相等的两个三角形全等.
(8)三边分别相等的两个三角形全等.
特别地:等式的有关性质和不等式的有关性质也作为公理
新知讲解
一、 同角(等角)的补角相等
二、 同角(等角)的余角相等
三、 三角形的任意两边之和大于第三边
新知讲解
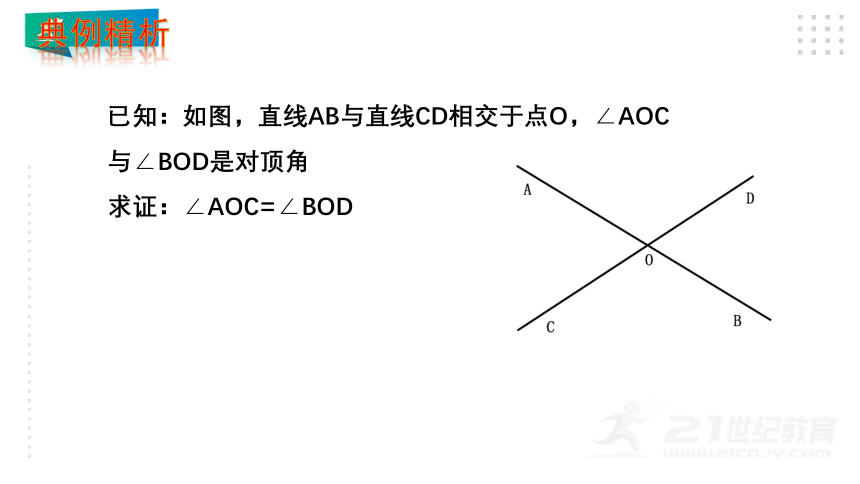
已知:如图,直线AB与直线CD相交于点O,∠AOC
与∠BOD是对顶角
求证:∠AOC=∠BOD
典例精析
证明:∵直线AB与直线CD相交于点O,
∴∠AOB和∠COD都是平角(平角的定义)
∴∠AOC和∠BOD都是∠AOD的补角(补角的定义)
∴∠AOC=∠BOD(同角的补角相等)
四、 对顶角相等
典例精析
1、请你完成定理“等角的补角相等”.
解:已知:∠1=∠2,∠3是∠1的余角,∠4是∠2的余角.
求证:∠3=∠4.
证明:∵∠3是∠1的余角,∠4是∠2的余角,
∴∠3=90°-∠1,∠4=90°-∠2.
又∵∠1=∠2,∴∠3=∠4.
典例精析
2.请你完成定理“三角形的任意两边之和大于第三边”.
已知:△ABC中,BC=a,AC=b,AB=c.
求证:a+b>c,a+c>b,b+c>a.
证明:假设a+b≤c,a+c≤b,b+c≤a,
则有a+b+a+c+b+c≤a+b+c,
整理可得a+b+c≤0,显然与已知矛盾,
假设不成立,
∴三角形的任意两边之和大于第三边.
典例精析
1、已知∠2是∠1的余角, ∠3是∠1的补角,若∠1=60°,,则∠2 = ,∠3 = .
2、下列命题中,属于公理的有( )
A.同角的补角相等. B.邻补角的平分线互相垂直.
C.两点之间,线段最短. D.直角三角形的两个锐角互余.
跟踪练习
30°
150°
C
3、某工程队,在修建广清高速公路时,有时需将弯曲的道路改直,
根据什么公理可以说明这样做能缩短路程( )
A.两点确定一条直线;
B.同一平面内, 过一点有且只有一条直线与已知直线垂直;
C.两点之间线段最短;
D.过直线外一点有且只有一条直线与这条直线平行.
4、命题“同角的余角相等”是( )
A.角的定义 B.假命题 C.公理 D.定理
跟踪练习
C
D
5.关于"垂线段最短",
有下列说法∶①是命题;②是假命题;③是真命题;④是定理.
其中正确的说法是( )
A.①③ B. ①③④ C.③④ D. ①②④
跟踪练习
B
6.如图,在△ABC和△DEF中,点B,E,C,F在同一直线上,下面有四个条件,请你从中选三个作为题设,余下的一个作为结论,写出一个正确的命题,并加以证明。
跟踪练习
①AB=DE;②AC=DF; . ③∠ABC=∠DEF;④BE=CF.
已知∶如图,在△ABC和△DEF中,
求证∶ (不能只填序号)
∠ABC=∠DEF
跟踪练习
命题
真命题
假命题(举反例)
公理(公认为正确)
定理(推理)
其它不常用的真命题(推理)
归纳总结
1、命题的真假
2、 欧几里得的《原本》
3、公理、定理、证明的相关含义
4、我们熟悉的公理以及等量代换
北师版八年级上册 平行线的证明
§7.2.2 定理与证明
1.理解公理和定理的意义,并能对公理与定理加以区别.
2.理解证明命题的思路、书写的格式,使学生对几何的重要内容之一——
推理论证,有初步的认识,从而培养思维的条理性和逻辑性.(重点)
知点
用我们以前学过的观察、实验、验证特例等方法.
这些方法往往不可靠.
能不能根据已经知道的真命题证实呢?
情境导入
那已经知道的真命题又是如何证实的?
哦……那可怎么办?
情境导入
其实,在数学发展史上,数学家们也遇到过类似的问题.公元前3世纪,人们已经积累了大量的数学知识,在此基础上,古希腊数学家欧几里得 (Euclid,公元前300年前后)编写了一本书,书名叫做《原本》(Elements). 为了说明每一结论的正确性,他在编写这本书时进行了大胆创造:挑选了一部分数
学名词和一部分公认的真命题作为证实其他命题的出发点和依据,其中的数学名词称为原名,公认的真命题称为公理(axiom).除了公理外,其他命题的真假都需要通过演绎推理的方法进行判断.
新知讲解
(1)两点确定一条直线.
(2)两点之间线段最短.
(3)同一平面内,过一点有且只有一条直线与已知直线垂直.
(4)两条直线被第三条直线所截,如果同位角相等,那么这两
条直线平行 (简述为:同位角相等,两直线平行).
(5)过直线外一点有且只有一条直线与这条直线平行.
(6)两边及其夹角分别相等的两个三角形全等.
新知讲解
(7)两角及其夹边分别相等的两个三角形全等.
(8)三边分别相等的两个三角形全等.
特别地:等式的有关性质和不等式的有关性质也作为公理
新知讲解
一、 同角(等角)的补角相等
二、 同角(等角)的余角相等
三、 三角形的任意两边之和大于第三边
新知讲解
已知:如图,直线AB与直线CD相交于点O,∠AOC
与∠BOD是对顶角
求证:∠AOC=∠BOD
典例精析
证明:∵直线AB与直线CD相交于点O,
∴∠AOB和∠COD都是平角(平角的定义)
∴∠AOC和∠BOD都是∠AOD的补角(补角的定义)
∴∠AOC=∠BOD(同角的补角相等)
四、 对顶角相等
典例精析
1、请你完成定理“等角的补角相等”.
解:已知:∠1=∠2,∠3是∠1的余角,∠4是∠2的余角.
求证:∠3=∠4.
证明:∵∠3是∠1的余角,∠4是∠2的余角,
∴∠3=90°-∠1,∠4=90°-∠2.
又∵∠1=∠2,∴∠3=∠4.
典例精析
2.请你完成定理“三角形的任意两边之和大于第三边”.
已知:△ABC中,BC=a,AC=b,AB=c.
求证:a+b>c,a+c>b,b+c>a.
证明:假设a+b≤c,a+c≤b,b+c≤a,
则有a+b+a+c+b+c≤a+b+c,
整理可得a+b+c≤0,显然与已知矛盾,
假设不成立,
∴三角形的任意两边之和大于第三边.
典例精析
1、已知∠2是∠1的余角, ∠3是∠1的补角,若∠1=60°,,则∠2 = ,∠3 = .
2、下列命题中,属于公理的有( )
A.同角的补角相等. B.邻补角的平分线互相垂直.
C.两点之间,线段最短. D.直角三角形的两个锐角互余.
跟踪练习
30°
150°
C
3、某工程队,在修建广清高速公路时,有时需将弯曲的道路改直,
根据什么公理可以说明这样做能缩短路程( )
A.两点确定一条直线;
B.同一平面内, 过一点有且只有一条直线与已知直线垂直;
C.两点之间线段最短;
D.过直线外一点有且只有一条直线与这条直线平行.
4、命题“同角的余角相等”是( )
A.角的定义 B.假命题 C.公理 D.定理
跟踪练习
C
D
5.关于"垂线段最短",
有下列说法∶①是命题;②是假命题;③是真命题;④是定理.
其中正确的说法是( )
A.①③ B. ①③④ C.③④ D. ①②④
跟踪练习
B
6.如图,在△ABC和△DEF中,点B,E,C,F在同一直线上,下面有四个条件,请你从中选三个作为题设,余下的一个作为结论,写出一个正确的命题,并加以证明。
跟踪练习
①AB=DE;②AC=DF; . ③∠ABC=∠DEF;④BE=CF.
已知∶如图,在△ABC和△DEF中,
求证∶ (不能只填序号)
∠ABC=∠DEF
跟踪练习
命题
真命题
假命题(举反例)
公理(公认为正确)
定理(推理)
其它不常用的真命题(推理)
归纳总结
1、命题的真假
2、 欧几里得的《原本》
3、公理、定理、证明的相关含义
4、我们熟悉的公理以及等量代换
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
