5.7 待定系数法+行程问题“三板斧” 课件(共34张PPT)
文档属性
| 名称 | 5.7 待定系数法+行程问题“三板斧” 课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 09:56:23 | ||
图片预览









文档简介
(共34张PPT)
北师版八年级上册 二元一次方程组
§5.7 待定系数法+行程问题“三板斧”
经过前边关于一次函数知识的不断深入学习。到本节课为止,学生已经对“待定系数法”比较熟悉。所以本节课不宜仅仅围绕教材内容进行讲解以及在计算的偏、难、怪方向设定讲授内容.易结合当前的考试热点和对学生思维能力的提升,学习习惯地深入培养这些方面着力。本人对本节课作了初步的改编——增设了与本节课内容相近的一次函数综合应用问题——行程问题“三板斧”。希望这个有益的尝试,能给各位同仁的教学带来裨益!
1.进一步理解二元一次方程与一次函数之间的联系,体会知识之间的普遍联系和知识之间的相互转化.
2.了解待定系数法,会用二元一次方程组确定一次函数的表达式.(重点)
3 . 学习完以上内容后,进一步探究掌握行程问题中的“三板斧”解题规律;
注意区分“同向而行”、“相向而行”的解题模型.(难点)
1、方程组 有 个解;
2、方程组 有 个解;
3、方程组 有 个解;
0
无数
一
温故知新
两条直线互相平行,有 交点;
两条直线重合,有 交点;
两条直线相交,有 交点;
0个
无数个
一个
温故知新
任意一个二元一次方程都可以转化成y=kx+b的形式,所以每个二元一次方程都对应一个一次函数.
温故知新
用二元一次方程组确定一次函数表达式
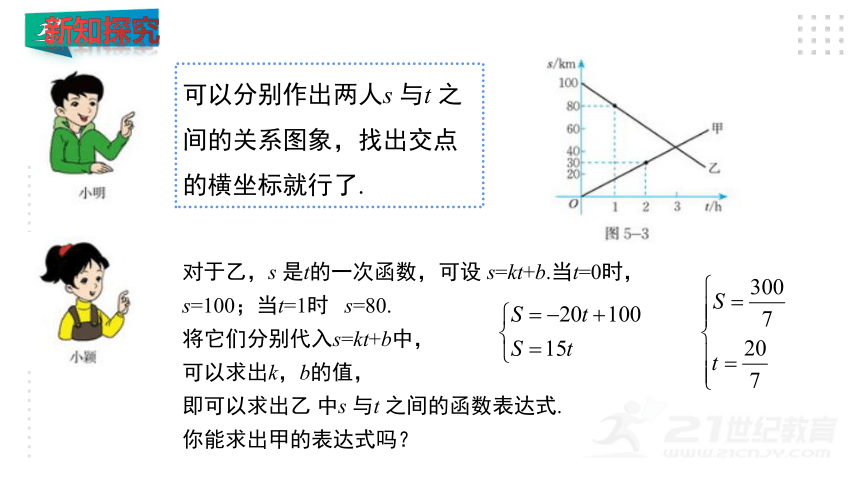
议一议:A ,B两地相距100千米,甲、乙两人骑车同时分别从A,B两地相向而行.假设他们都保持匀速行驶,则他们各自到A地的距离 s(千米)都是骑车时间 t (时)的一次函数.1小时后乙距A地80千米; 2小时后甲距A地30千米.
问:经过多长时间两人相遇 说出你的方法,并与同学们交流.
1小时后
2小时后甲距A地30千米
乙距A地80千米
甲
A
乙
B
情境导入
可以分别作出两人s 与t 之间的关系图象,找出交点的横坐标就行了.
新知探究
对于乙,s 是t的一次函数,可设 s=kt+b.当t=0时,s=100;当t=1时 s=80.
将它们分别代入s=kt+b中,
可以求出k,b的值,
即可以求出乙 中s 与t 之间的函数表达式.
你能求出甲的表达式吗?
新知探究
1 时后乙距A地 80千米,即乙的速度是20千米/时
2 时后甲距A 地 30千米,故甲的速度是15千米/时
设同时出发后t小时相遇,则15t+20t=100
用一元一次方程的方法可以解决问题
用图象法可以解决问题
用方程组的方法可以解决问题
用作图象的方法可以直观地获得问题的结果,但有时却难以准确,为了获得准确的结果,我们一般用代数方法.
在以上的解题过程中你受到什么启发?
小明
小颖
合作共学
某长途汽车客运站规定,乘客可以免费携带一定质量的行李,但超过该
质量则需购买行李票,且行李费y(元)是行李质量x(kg)的一次函数.
已知李明带了60 kg的行李,交了行李费5元;张华带了90 kg的行李,交了行李费10元.
(1)写出y与x之间的函数表达式;
(2)旅客最多可免费携带多少千克的行李?
典例精讲
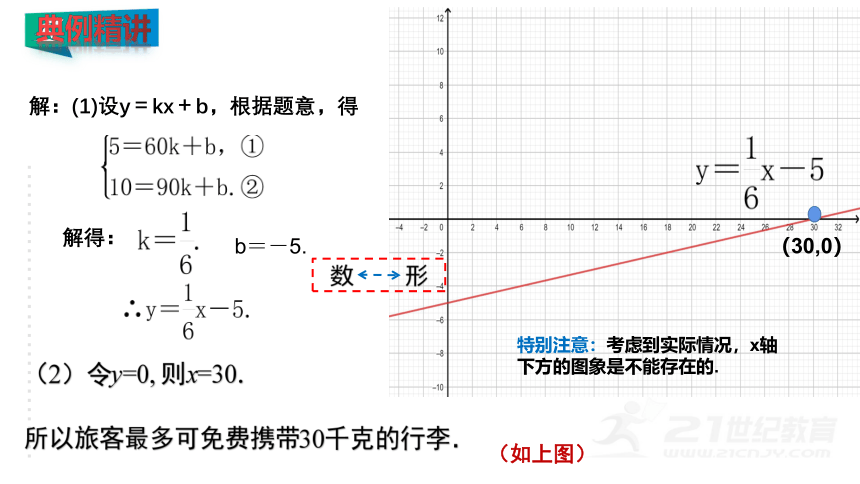
解:(1)设y=kx+b,根据题意,得
解得:
b=-5.
(2)令y=0, 则x=30.
所以旅客最多可免费携带30千克的行李.
典例精讲
(30,0)
(如上图)
特别注意:考虑到实际情况,x轴下方的图象是不能存在的.
数 形
像这样,先设出函数表达式,再根据所给条件确定表达式中未知的系数,从而得到函数表达式的方法,叫做待定系数法.
利用二元一次方程组求一次函数表达式的一般步骤:
1.用含字母的系数设出一次函数的表达式:y=kx+b.
2.将已知条件代入上述表达式中得k,b的二元一次方程组.
3.解这个二元一次方程组得k,b.
4.进而求出一次函数的表达式.
归纳总结
设
代
解
列
解方程组得
已知一次函数的图象过点(3,5)与(-4,-9),
求这个一次函数的解析式.
解:设这个一次函数的解析式为y=kx+b.
3k+b=5,
﹣4k+b=﹣9,
∴这个一次函数的解析式为
把点(3,5)与(﹣4,9)分别代入,得:
k=2,
y=2x-1.
典例精讲
设
代
解
列
b=﹣1
1、右图中的两条直线L1,L2的交点坐标可以看做方程组_ ___的解.
跟踪练习
2.在弹性限度内,弹簧的长度y(cm)是所挂物体质量x(kg)的一次函数.当所挂物体的质量为1kg 时,弹簧长 15 cm;当所挂物体的质量为3kg时,弹簧长16cm.写出y与x之间的关系 .
y=0.5x+14.5
一次函数综合应用初步
行程问题“三板斧”
板斧一“k”与“速度”
星期天,小明参加南沙自行车协会组织的“南沙横琴骑行游”活动,早上8:00出发骑车从南沙前往珠海横琴.2小时后,爸爸骑摩托车沿同一线路也从南沙前往横琴,他们的行驶路程y(千米)与小明的行驶时间x(小时)之间的函数关系如图所示,下列说法不正确的是( )
A.南沙与横琴两地相距60千米
B.11:00时,爸爸和小明在途中相遇
C.爸爸骑摩托车的平均速度是60千米/小时
D.爸爸比小明早到横琴1小时
C
解析:
一、可分别设父亲的运动图象函数表达式为:
y1=k1x+b
小明的运动图象函数表达式:
y2=k2x
小明运动图象
父亲运动图象
y2=
二、依据图象中的条件
可求出 y1=40x-80;
三、依据图象中的条件可以发现:父亲的速度=60÷(3.5-2)=40(千米/小时)
小明的速度=60÷4.5= (千米/小时)
板斧一“k”与“速度”
规律探究
如右下图,若纵轴表示物体运动的距离,横轴表示运动时间。则图象的 和速度值相等
板斧一“k”与“速度”
在一条笔直的公路旁依次有A、B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.设甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图所示,请回答下列问题:
(1)A、C两村间的距离为 km,a= ;
(2)求出图中点P的坐标,并解释该点坐标所表示的实际意义;
(3)乙在行驶过程中,何时距甲10km?
典例精析1
同向而行
解:(1)依题意可知:
A,C距离120千米;
甲的速度为(120-90)÷0.5=60(千米/小时)
乙的速度为 90÷3=30(千米/小时) a=120÷60=2(小时)
(2)求快车返回过程中 y(千米)与 x(小时)的函数关系式;
解:设 y甲=kx+b y乙=k1x+b1
因为甲、乙的速度分别为60千米/小时,30千米/小时。
∴k=-60,k1=-30
又∵图象分别经过点(0,120),
(0.90)
代入得:b=120,b1=90
∴y甲=-60x+120 y乙=-30x+90
典例精析1
令y甲=y乙
则-60x+120 =-30x+90
解得,x=1,y=60
∴P(1,60)
表示经过1h甲,乙相遇距C村60千米.
(3)乙在行驶过程中,何时距甲10km?
板斧二“间隔距离问题”
分析:因为两人均向C村移动,且y轴表示的实际意义均为二者离C村的距离.所以二者的距离差即是运动过程中,他们的间隔距离。
①
②
位置①对应的时间点t1可以根据 y甲-y乙 =10的方式求出;
位置②对应的时间点t2可以根据 y乙-y甲=10的方式求出;
位置③对应的时间点t3可以根据 y乙=10 的方式求出.(甲先到)
③
(1)间隔距离=离终点的距离之差(上-下).
(2)慢者剩余路程=间隔距离
用此计算模型可以解决同向而行中的间隔距离问题.
板斧二“间隔距离问题”
同向而行
(3)乙在行驶过程中,何时距甲10km?
①
②
解:设 y乙=kx+b
因为乙的速度为30千米/小时。∴k=-30
又∵图象经过点(0,90)
代入得:b=90.
∴y乙=-30x+90
∴分别有y甲-y乙=10;
y乙-y甲=10;
y乙=10
解得:x= 或 或 .
综上可知:x= 或 或 ,乙距
甲10千米
典例精析1
③
典例精析2
某学校开展“青少年科技创新比赛”活动,“喜洋洋”代表队设计了一个遥控车沿直线轨道AC做匀速直线运动的模型。甲、乙两车同时分别从A,B两处出发,沿轨道到达C处,B在AC 上,甲的速度是乙的速度的1.5倍,设t(分)后甲、乙两遥控车与B处的距离分别为d1,d2,则,d1,d2与t的函数关系如图,试根据图象解决下列问题。
(1)填空:乙的速度V2_____米/分。(2分)
(2)写出d1与t的函数关系式。(3分)
解析:如图可求出乙的速度:120÷3=40米/分
则甲的速度:40×1.5=60米/分
∴可以发现甲、乙运动函数表达式中的k甲=-60和k甲=60;
k乙=40
40
同向而行
(2)如图,由题意可设 d1=k1t+b(x≤a); d2=k2t
∵V甲=60米/分,V乙=40米/分,且d1图象经过了(0,60)
∴可得k1=-60,b=60;k2=40
∴d1=-60t+60(x≤a);
d2=40t
典例精析2
同向而行
(3)若甲、乙两遥控车的距离超过10米时信号不会产生相互干扰,试探求什么时间两遥控车的信号不会产生相互干扰。(4分)
板斧二“间隔距离问题”
解析:本题中的纵轴d表示的意义不是两辆遥控车离终点C的距离,而是离B地的距离。所以,如果想利用上述模型解题,需找出相差10米时的各个时刻二者离C的距离。
甲离C地(终点)的距离=180-60t;
乙离C地(终点)的距离=120-40t
甲、乙相遇前:180-60t-(120-40t)=10;
甲、乙相遇后:120-40t-(180-60t)=10;
乙距终点C10米:120-40t=10
(3)若甲、乙两遥控车的距离超过10米时信号不会产生相互干扰,试探求什么时间两遥控车的信号不会产生相互干扰。(4分)
解:由题意可得:
甲离C地:180-60t; 乙离C地120-40t
所以有:
(1)180-60t-(120-40t)=10;
(2) 120-40t-(180-60t)=10;
(3) 120-40t=10
解得:t=2.5分或3.5分或2.75分
∵两车3分钟时相遇了。∴后两种情况不成立.
又∵距离超过10米才无干扰,
∴0≤t<2.5
典例精析2
快、慢两车分别从相距 180 千米的甲、乙两地同时出发,沿同一路线匀速行驶,相向而行,快车到达乙地停留一段时间后,按原路原速返回甲地.慢车到达甲地比快车到达甲地早 小时,慢车速度是快车速度的一半,快、慢两车到达甲地后停止行驶,两车距各自出发地的路程 y(千米)与所用时间 x(小时)的函数图象如图所示,请结合图象信息解答下列问题:
(1)请直接写出快、慢两车的速度;
(2)求快车返回过程中 y(千米)与 x(小时)的函数关系式;
典例精析3
解:(1)依题意可求出慢车速度:180÷3=60(千米/小时);
快车速度:60×2=120(千米/小时)
相向而行
(2)求快车返回过程中 y(千米)与 x(小时)的函数关系式;
解:设直线CD为 y=kx+b
因为快车速度未变。∴k=-120
又∵直线CD经过点
∴代入得:b=420
∴y=-120x+420.
典例精析3
相向而行
(3)两车出发后经过多长时间相距 90 千米的路程?直接写出答案.
板斧三“间隔距离问题”
解析:相向而行时
(1)相遇前:总路程-二者的路程和=90千米。
(2)相遇后:二者路程和-总路程=90千米
同向而行时(快车已经折返)
yCD-yOA=90千米
(1)间隔距离=总路程与路程和的差.
(2)间隔距离=二者距终点的路程差(同向时)
用此计算模型可以解决相向而行中的间隔距离问题.
板斧三“间隔距离问题”
相向而行
(3)两车出发后经过多长时间相距 90 千米的路程?直接写出答案.
典例精析3
解:由题意可得:
相遇前:快车所走路程=120t;
慢车所走路程=60t
∴(1)180-(120t+60t)=90;
(2) (120t+60t)-180=90
(3)(-120x+420)-60t=90
解得:t=0.5小时或1.5小时或2.5小时.
综上可知:t=0.5小时或1.5小时或2.5小时,两车相距90千米.
本节课重点学习了两个内容:
1、待定系数法求一次函数表达式;
2、增设了一次函数综合应用问题中的“行程问题”。并总结了
相应的解题模型——
间隔距离=路程差
同向而行.
相向而行.
3、特别的:通常情况下,行程问题里函数表达式中的 =物体运动的速度
北师版八年级上册 二元一次方程组
§5.7 待定系数法+行程问题“三板斧”
经过前边关于一次函数知识的不断深入学习。到本节课为止,学生已经对“待定系数法”比较熟悉。所以本节课不宜仅仅围绕教材内容进行讲解以及在计算的偏、难、怪方向设定讲授内容.易结合当前的考试热点和对学生思维能力的提升,学习习惯地深入培养这些方面着力。本人对本节课作了初步的改编——增设了与本节课内容相近的一次函数综合应用问题——行程问题“三板斧”。希望这个有益的尝试,能给各位同仁的教学带来裨益!
1.进一步理解二元一次方程与一次函数之间的联系,体会知识之间的普遍联系和知识之间的相互转化.
2.了解待定系数法,会用二元一次方程组确定一次函数的表达式.(重点)
3 . 学习完以上内容后,进一步探究掌握行程问题中的“三板斧”解题规律;
注意区分“同向而行”、“相向而行”的解题模型.(难点)
1、方程组 有 个解;
2、方程组 有 个解;
3、方程组 有 个解;
0
无数
一
温故知新
两条直线互相平行,有 交点;
两条直线重合,有 交点;
两条直线相交,有 交点;
0个
无数个
一个
温故知新
任意一个二元一次方程都可以转化成y=kx+b的形式,所以每个二元一次方程都对应一个一次函数.
温故知新
用二元一次方程组确定一次函数表达式
议一议:A ,B两地相距100千米,甲、乙两人骑车同时分别从A,B两地相向而行.假设他们都保持匀速行驶,则他们各自到A地的距离 s(千米)都是骑车时间 t (时)的一次函数.1小时后乙距A地80千米; 2小时后甲距A地30千米.
问:经过多长时间两人相遇 说出你的方法,并与同学们交流.
1小时后
2小时后甲距A地30千米
乙距A地80千米
甲
A
乙
B
情境导入
可以分别作出两人s 与t 之间的关系图象,找出交点的横坐标就行了.
新知探究
对于乙,s 是t的一次函数,可设 s=kt+b.当t=0时,s=100;当t=1时 s=80.
将它们分别代入s=kt+b中,
可以求出k,b的值,
即可以求出乙 中s 与t 之间的函数表达式.
你能求出甲的表达式吗?
新知探究
1 时后乙距A地 80千米,即乙的速度是20千米/时
2 时后甲距A 地 30千米,故甲的速度是15千米/时
设同时出发后t小时相遇,则15t+20t=100
用一元一次方程的方法可以解决问题
用图象法可以解决问题
用方程组的方法可以解决问题
用作图象的方法可以直观地获得问题的结果,但有时却难以准确,为了获得准确的结果,我们一般用代数方法.
在以上的解题过程中你受到什么启发?
小明
小颖
合作共学
某长途汽车客运站规定,乘客可以免费携带一定质量的行李,但超过该
质量则需购买行李票,且行李费y(元)是行李质量x(kg)的一次函数.
已知李明带了60 kg的行李,交了行李费5元;张华带了90 kg的行李,交了行李费10元.
(1)写出y与x之间的函数表达式;
(2)旅客最多可免费携带多少千克的行李?
典例精讲
解:(1)设y=kx+b,根据题意,得
解得:
b=-5.
(2)令y=0, 则x=30.
所以旅客最多可免费携带30千克的行李.
典例精讲
(30,0)
(如上图)
特别注意:考虑到实际情况,x轴下方的图象是不能存在的.
数 形
像这样,先设出函数表达式,再根据所给条件确定表达式中未知的系数,从而得到函数表达式的方法,叫做待定系数法.
利用二元一次方程组求一次函数表达式的一般步骤:
1.用含字母的系数设出一次函数的表达式:y=kx+b.
2.将已知条件代入上述表达式中得k,b的二元一次方程组.
3.解这个二元一次方程组得k,b.
4.进而求出一次函数的表达式.
归纳总结
设
代
解
列
解方程组得
已知一次函数的图象过点(3,5)与(-4,-9),
求这个一次函数的解析式.
解:设这个一次函数的解析式为y=kx+b.
3k+b=5,
﹣4k+b=﹣9,
∴这个一次函数的解析式为
把点(3,5)与(﹣4,9)分别代入,得:
k=2,
y=2x-1.
典例精讲
设
代
解
列
b=﹣1
1、右图中的两条直线L1,L2的交点坐标可以看做方程组_ ___的解.
跟踪练习
2.在弹性限度内,弹簧的长度y(cm)是所挂物体质量x(kg)的一次函数.当所挂物体的质量为1kg 时,弹簧长 15 cm;当所挂物体的质量为3kg时,弹簧长16cm.写出y与x之间的关系 .
y=0.5x+14.5
一次函数综合应用初步
行程问题“三板斧”
板斧一“k”与“速度”
星期天,小明参加南沙自行车协会组织的“南沙横琴骑行游”活动,早上8:00出发骑车从南沙前往珠海横琴.2小时后,爸爸骑摩托车沿同一线路也从南沙前往横琴,他们的行驶路程y(千米)与小明的行驶时间x(小时)之间的函数关系如图所示,下列说法不正确的是( )
A.南沙与横琴两地相距60千米
B.11:00时,爸爸和小明在途中相遇
C.爸爸骑摩托车的平均速度是60千米/小时
D.爸爸比小明早到横琴1小时
C
解析:
一、可分别设父亲的运动图象函数表达式为:
y1=k1x+b
小明的运动图象函数表达式:
y2=k2x
小明运动图象
父亲运动图象
y2=
二、依据图象中的条件
可求出 y1=40x-80;
三、依据图象中的条件可以发现:父亲的速度=60÷(3.5-2)=40(千米/小时)
小明的速度=60÷4.5= (千米/小时)
板斧一“k”与“速度”
规律探究
如右下图,若纵轴表示物体运动的距离,横轴表示运动时间。则图象的 和速度值相等
板斧一“k”与“速度”
在一条笔直的公路旁依次有A、B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.设甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图所示,请回答下列问题:
(1)A、C两村间的距离为 km,a= ;
(2)求出图中点P的坐标,并解释该点坐标所表示的实际意义;
(3)乙在行驶过程中,何时距甲10km?
典例精析1
同向而行
解:(1)依题意可知:
A,C距离120千米;
甲的速度为(120-90)÷0.5=60(千米/小时)
乙的速度为 90÷3=30(千米/小时) a=120÷60=2(小时)
(2)求快车返回过程中 y(千米)与 x(小时)的函数关系式;
解:设 y甲=kx+b y乙=k1x+b1
因为甲、乙的速度分别为60千米/小时,30千米/小时。
∴k=-60,k1=-30
又∵图象分别经过点(0,120),
(0.90)
代入得:b=120,b1=90
∴y甲=-60x+120 y乙=-30x+90
典例精析1
令y甲=y乙
则-60x+120 =-30x+90
解得,x=1,y=60
∴P(1,60)
表示经过1h甲,乙相遇距C村60千米.
(3)乙在行驶过程中,何时距甲10km?
板斧二“间隔距离问题”
分析:因为两人均向C村移动,且y轴表示的实际意义均为二者离C村的距离.所以二者的距离差即是运动过程中,他们的间隔距离。
①
②
位置①对应的时间点t1可以根据 y甲-y乙 =10的方式求出;
位置②对应的时间点t2可以根据 y乙-y甲=10的方式求出;
位置③对应的时间点t3可以根据 y乙=10 的方式求出.(甲先到)
③
(1)间隔距离=离终点的距离之差(上-下).
(2)慢者剩余路程=间隔距离
用此计算模型可以解决同向而行中的间隔距离问题.
板斧二“间隔距离问题”
同向而行
(3)乙在行驶过程中,何时距甲10km?
①
②
解:设 y乙=kx+b
因为乙的速度为30千米/小时。∴k=-30
又∵图象经过点(0,90)
代入得:b=90.
∴y乙=-30x+90
∴分别有y甲-y乙=10;
y乙-y甲=10;
y乙=10
解得:x= 或 或 .
综上可知:x= 或 或 ,乙距
甲10千米
典例精析1
③
典例精析2
某学校开展“青少年科技创新比赛”活动,“喜洋洋”代表队设计了一个遥控车沿直线轨道AC做匀速直线运动的模型。甲、乙两车同时分别从A,B两处出发,沿轨道到达C处,B在AC 上,甲的速度是乙的速度的1.5倍,设t(分)后甲、乙两遥控车与B处的距离分别为d1,d2,则,d1,d2与t的函数关系如图,试根据图象解决下列问题。
(1)填空:乙的速度V2_____米/分。(2分)
(2)写出d1与t的函数关系式。(3分)
解析:如图可求出乙的速度:120÷3=40米/分
则甲的速度:40×1.5=60米/分
∴可以发现甲、乙运动函数表达式中的k甲=-60和k甲=60;
k乙=40
40
同向而行
(2)如图,由题意可设 d1=k1t+b(x≤a); d2=k2t
∵V甲=60米/分,V乙=40米/分,且d1图象经过了(0,60)
∴可得k1=-60,b=60;k2=40
∴d1=-60t+60(x≤a);
d2=40t
典例精析2
同向而行
(3)若甲、乙两遥控车的距离超过10米时信号不会产生相互干扰,试探求什么时间两遥控车的信号不会产生相互干扰。(4分)
板斧二“间隔距离问题”
解析:本题中的纵轴d表示的意义不是两辆遥控车离终点C的距离,而是离B地的距离。所以,如果想利用上述模型解题,需找出相差10米时的各个时刻二者离C的距离。
甲离C地(终点)的距离=180-60t;
乙离C地(终点)的距离=120-40t
甲、乙相遇前:180-60t-(120-40t)=10;
甲、乙相遇后:120-40t-(180-60t)=10;
乙距终点C10米:120-40t=10
(3)若甲、乙两遥控车的距离超过10米时信号不会产生相互干扰,试探求什么时间两遥控车的信号不会产生相互干扰。(4分)
解:由题意可得:
甲离C地:180-60t; 乙离C地120-40t
所以有:
(1)180-60t-(120-40t)=10;
(2) 120-40t-(180-60t)=10;
(3) 120-40t=10
解得:t=2.5分或3.5分或2.75分
∵两车3分钟时相遇了。∴后两种情况不成立.
又∵距离超过10米才无干扰,
∴0≤t<2.5
典例精析2
快、慢两车分别从相距 180 千米的甲、乙两地同时出发,沿同一路线匀速行驶,相向而行,快车到达乙地停留一段时间后,按原路原速返回甲地.慢车到达甲地比快车到达甲地早 小时,慢车速度是快车速度的一半,快、慢两车到达甲地后停止行驶,两车距各自出发地的路程 y(千米)与所用时间 x(小时)的函数图象如图所示,请结合图象信息解答下列问题:
(1)请直接写出快、慢两车的速度;
(2)求快车返回过程中 y(千米)与 x(小时)的函数关系式;
典例精析3
解:(1)依题意可求出慢车速度:180÷3=60(千米/小时);
快车速度:60×2=120(千米/小时)
相向而行
(2)求快车返回过程中 y(千米)与 x(小时)的函数关系式;
解:设直线CD为 y=kx+b
因为快车速度未变。∴k=-120
又∵直线CD经过点
∴代入得:b=420
∴y=-120x+420.
典例精析3
相向而行
(3)两车出发后经过多长时间相距 90 千米的路程?直接写出答案.
板斧三“间隔距离问题”
解析:相向而行时
(1)相遇前:总路程-二者的路程和=90千米。
(2)相遇后:二者路程和-总路程=90千米
同向而行时(快车已经折返)
yCD-yOA=90千米
(1)间隔距离=总路程与路程和的差.
(2)间隔距离=二者距终点的路程差(同向时)
用此计算模型可以解决相向而行中的间隔距离问题.
板斧三“间隔距离问题”
相向而行
(3)两车出发后经过多长时间相距 90 千米的路程?直接写出答案.
典例精析3
解:由题意可得:
相遇前:快车所走路程=120t;
慢车所走路程=60t
∴(1)180-(120t+60t)=90;
(2) (120t+60t)-180=90
(3)(-120x+420)-60t=90
解得:t=0.5小时或1.5小时或2.5小时.
综上可知:t=0.5小时或1.5小时或2.5小时,两车相距90千米.
本节课重点学习了两个内容:
1、待定系数法求一次函数表达式;
2、增设了一次函数综合应用问题中的“行程问题”。并总结了
相应的解题模型——
间隔距离=路程差
同向而行.
相向而行.
3、特别的:通常情况下,行程问题里函数表达式中的 =物体运动的速度
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
