4.3.3 余角和补角 课件(共32张PPT)
文档属性
| 名称 | 4.3.3 余角和补角 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-08 00:00:00 | ||
图片预览










文档简介
(共32张PPT)
第四章 几何图形初步
4.3.3 余角和补角
随堂演练
课堂小结
例题讲解
情景导入
获取新知
比萨斜塔建于1173年,工程曾间断了两次,历经约二百年才完工,设计为垂直建造,但是在工程开始后不久便由于地基不均匀和土层松软而倾斜,你知道比萨斜塔倾斜多少度角吗?它现在与地面成多少度角?
倾斜了约3.97°.
它现在与地面成的夹角约是86.03°.
这两个角之和是多少
情景导入
获取新知
知识点1:余角和补角的概念
将一张长方形纸片,沿一个角折叠后,折痕与长方形的边形成了4个角.
1
2
3
4
思考:
1. ∠1 与∠2 有什么数量关系?
∠1+∠2 = 90°
2. ∠3与∠4有什么数量关系?
∠3+∠4 = 180°
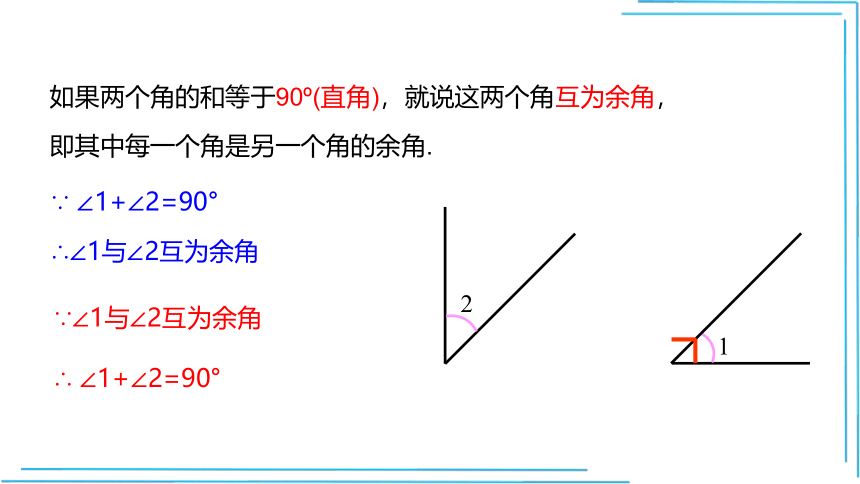
如果两个角的和等于90 (直角),就说这两个角互为余角,
即其中每一个角是另一个角的余角.
1
2
∵ ∠1+∠2=90°
∴∠1与∠2互为余角
∵∠1与∠2互为余角
∴ ∠1+∠2=90°
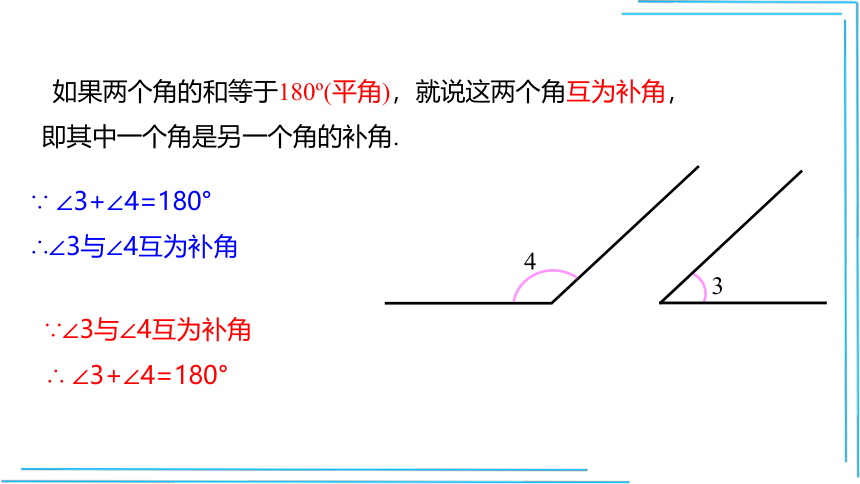
如果两个角的和等于180 (平角),就说这两个角互为补角,即其中一个角是另一个角的补角.
4
3
∵ ∠3+∠4=180°
∴∠3与∠4互为补角
∵∠3与∠4互为补角
∴ ∠3+∠4=180°
如果 ∠1 与∠2互余,那么∠1 的余角是∠2,同样∠2的余角是∠1 ; 如果∠1 与∠2互补,那么∠1 的补角是∠2, 同样∠2的补角是∠1 。
两角互余或互补,只与角的度数有关,与位置无关。
思考1:定义中的“互为”一词如何理解?
思考2:互余、互补的两角是否一定有公共顶点或公共边?
备注:互余,互补必须是两个角之间的关系.
例题讲解
例1 如图,点A,O, B在同一条直线 上,射线OD和射线
OE分别平分∠AOC和∠BOC, 图中哪些角互为余角?
解:因为点A,O, B在同一条直线上,
所以 ∠AOC和∠BOC互为补角.
又因为射线OD和射线OE分别平分∠AOC和∠BOC,
所以∠COD+∠COE= ∠AOC+ ∠BOC
= (∠AOC+∠BOC)= 90°.
所以,∠COD和∠COE互为余角,
同理,∠AOD和∠BOE,∠AOD和∠COE,
∠COD和∠BOE也互为余角.
O
A
B
C
D
E
例2 已知 ∠A 与∠B 互余,且 ∠A 的度数比∠B 度数的 3 倍还多30°,求∠B的度数.
解:设∠B的度数为x°,则 ∠A 的度数为(3x+30)°.
根据题意得:
x + ( 3x+30 ) = 90.
解得 x=15.
故 ∠B 的度数为15°.
知识点2:余角和补角的性质
思考1:如果∠1与∠2,∠3都互为补角,∠2和∠3的大小有什么关系?
因为∠1与∠2,∠3都互为补角,
所以∠2=180°-∠1,∠3=180°-∠1,
所以∠2=∠3.
同角的补角相等.
类似地,可以得到:
等角的补角相等.
思考2:如果∠1与∠2,∠3 都互为余角,∠2和∠3的大小又有什么关系?
因为∠1与∠2,∠3都互为余角,
所以∠2=90°-∠1,∠3=90°-∠1,
所以∠2=∠3.
同角的余角相等.
类似地,可以得到:
等角的余角相等.
同角的补角相等,
即:若∠A+∠B=180°,
∠A+∠C=180°,
则∠B=∠C.
等角的补角相等,
即:若∠A+∠B=180°,
∠D+∠C= 180°,
∠A=∠D,
则∠B=∠C.
同角的余角相等,
即:若∠A+∠B=90°,
∠A+∠C=90°,
则∠B=∠C.
等角的余角相等,
即:若∠A+∠B=90°,
∠D+∠C=90°,
∠A=∠D,
则∠B=∠C.
互为余角 互为补角
对应图形
数量关系
性 质
∠1+ ∠2 = 90 °
∠1+ ∠2 = 180 °
同角或等角的余角相等
同角或等角的补角相等
1
2
1
2
例题讲解
例3 如图①,直线AB与∠COD的两边OC,OD分别相交于点E,
F,∠1+∠2=180°.找出图中与∠2相等的角,并说明理由.
导引:已知∠1+∠2=180°,说明∠2是∠1的补角.根据同角
(或等角)的补角相等,找出图中∠1的其他补角和∠2的其他补角
的补角,便可确定与∠2相等的角.
解:如图②,因为∠1+∠3=180°,∠1+∠2=180°,
所以∠3=∠2.
因为∠1+∠4=180°,∠1+∠2=180°,
所以∠4=∠2.
因为∠2+∠5=180°,
∠6+∠5=180°,
所以∠2=∠6.
所以图中与∠2相等的角
有∠3,∠4,∠6.
1.定义:以正北、正南方向为基准,描述物体运动的方向,即正北、正南方向与物体运动方向的夹角为方位角.
注意事项:方位角在叙述时,一般先说南北,后说东西,
如南偏东30°.但与南北方向夹角为45°时,常简称为东北、东南、西北、西南,如南偏东45°,即为东南方向.
知识点3:方位角
东
西
北
南
O
正东:
正南:
正西:
正北:
西北方向:
西南方向:
东北方向:
东南方向:
射线 OA
A
B
C
D
45°
E
G
F
H
45°
八大方位
45°
45°
射线 OB
射线 OC
射线 OD
射线 OE
射线 OF
射线 OH
射线 OG
甲地
乙地
北
观测点
被观测点
如何表示在甲地观察乙地的方位角?
1.先找到观测点,然后画出方向指标;
甲地
乙地
北
视线
2.把观测点和被观测点用线段连接起来;
如何表示在甲地观察乙地的方位角?
甲地
乙地
北
方位角
如何表示在甲地观察乙地的方位角?
3.度量正北或正南方向的射线和视线之间的角度,就是所求方位角了。
例4 如图,货轮O在航行过程中,发现灯塔A在它南偏东60 的方向上.同时,在它北偏东40 、南偏西10 、西北(即北偏西45 )方向上又分别发现了客轮B、货轮C和海岛D.仿照表示灯塔方位的方法,画出表示客轮B、货轮C和海岛D方向的射线.
画法:以点O为顶点,表示正北方向的射线为角的一边,画40°的角,使它的另一边OB落在东和北之间.射线OB的方向就是北偏东40°,即客轮B所在的方向.同理,可以画出表示货轮C和海岛D方向的射线.
东
南
西
北
60°
● B
40°
10°
45°
C ●
● D
O
●
● A
随堂演练
1.一个角的余角是它的2倍,这个角的度数是( )
A.30° B.45° C.60° D.75°
A
2.如果一个角是56°,那么下列说法中正确的是( )
A.它的余角是44° B.它的补角是44°
C.它的余角是124° D.它的补角是124°
D
3. 如图,直线AB,CD交于点O,因为∠1+∠3=180°,∠2+∠3=180°,所以∠1=∠2的依据是( )
A.同角的余角相等
B.等角的余角相等
C.同角的补角相等
D.等角的补角相等
C
4. 如图,下面说法中不正确的是( )
A.射线OA表示北偏东30°
B.射线OB表示西北方向
C.射线OC表示西偏南80°
D.射线OD表示南偏东70°
C
5. ∠1 与 ∠2 互余,∠1 = (6x + 8)°,∠2 = (4x-8)°,
则∠1= ,∠2= .
62°
28°
6. 一个角的补角比它的余角的3倍小20°,求这个角的度数.
解:设这个角的度数为x°.
由题意,得180-x=3(90-x)-20,
解得x=35.
答:这个角的度数为35°.
7. 如图,D是直线EF上一点,∠CDE=90°,∠1=∠2,哪些角互为余角?哪些角互为补角?
解:∠1与∠ADC,∠1与∠BDC,∠2与∠BDC,∠2与∠ADC互为余角;
∠1与∠ADF,∠2与∠ADF,∠2与∠BDE,∠1与∠BDE,∠EDC与∠FDC互为补角.
课堂小结
余角和补角
余角
补角
两个角的和等于90
两个角的和等于180
定义
性质
同(等)角的余角相等
定义
性质
同(等)角的补角相等
方位角
正北、正南方向与物体运动方向的夹角为方位角
表示方向的角在航 行、测绘等工作中经常 用到
定义
应用
https://www.21cnjy.com/help/help_extract.php
第四章 几何图形初步
4.3.3 余角和补角
随堂演练
课堂小结
例题讲解
情景导入
获取新知
比萨斜塔建于1173年,工程曾间断了两次,历经约二百年才完工,设计为垂直建造,但是在工程开始后不久便由于地基不均匀和土层松软而倾斜,你知道比萨斜塔倾斜多少度角吗?它现在与地面成多少度角?
倾斜了约3.97°.
它现在与地面成的夹角约是86.03°.
这两个角之和是多少
情景导入
获取新知
知识点1:余角和补角的概念
将一张长方形纸片,沿一个角折叠后,折痕与长方形的边形成了4个角.
1
2
3
4
思考:
1. ∠1 与∠2 有什么数量关系?
∠1+∠2 = 90°
2. ∠3与∠4有什么数量关系?
∠3+∠4 = 180°
如果两个角的和等于90 (直角),就说这两个角互为余角,
即其中每一个角是另一个角的余角.
1
2
∵ ∠1+∠2=90°
∴∠1与∠2互为余角
∵∠1与∠2互为余角
∴ ∠1+∠2=90°
如果两个角的和等于180 (平角),就说这两个角互为补角,即其中一个角是另一个角的补角.
4
3
∵ ∠3+∠4=180°
∴∠3与∠4互为补角
∵∠3与∠4互为补角
∴ ∠3+∠4=180°
如果 ∠1 与∠2互余,那么∠1 的余角是∠2,同样∠2的余角是∠1 ; 如果∠1 与∠2互补,那么∠1 的补角是∠2, 同样∠2的补角是∠1 。
两角互余或互补,只与角的度数有关,与位置无关。
思考1:定义中的“互为”一词如何理解?
思考2:互余、互补的两角是否一定有公共顶点或公共边?
备注:互余,互补必须是两个角之间的关系.
例题讲解
例1 如图,点A,O, B在同一条直线 上,射线OD和射线
OE分别平分∠AOC和∠BOC, 图中哪些角互为余角?
解:因为点A,O, B在同一条直线上,
所以 ∠AOC和∠BOC互为补角.
又因为射线OD和射线OE分别平分∠AOC和∠BOC,
所以∠COD+∠COE= ∠AOC+ ∠BOC
= (∠AOC+∠BOC)= 90°.
所以,∠COD和∠COE互为余角,
同理,∠AOD和∠BOE,∠AOD和∠COE,
∠COD和∠BOE也互为余角.
O
A
B
C
D
E
例2 已知 ∠A 与∠B 互余,且 ∠A 的度数比∠B 度数的 3 倍还多30°,求∠B的度数.
解:设∠B的度数为x°,则 ∠A 的度数为(3x+30)°.
根据题意得:
x + ( 3x+30 ) = 90.
解得 x=15.
故 ∠B 的度数为15°.
知识点2:余角和补角的性质
思考1:如果∠1与∠2,∠3都互为补角,∠2和∠3的大小有什么关系?
因为∠1与∠2,∠3都互为补角,
所以∠2=180°-∠1,∠3=180°-∠1,
所以∠2=∠3.
同角的补角相等.
类似地,可以得到:
等角的补角相等.
思考2:如果∠1与∠2,∠3 都互为余角,∠2和∠3的大小又有什么关系?
因为∠1与∠2,∠3都互为余角,
所以∠2=90°-∠1,∠3=90°-∠1,
所以∠2=∠3.
同角的余角相等.
类似地,可以得到:
等角的余角相等.
同角的补角相等,
即:若∠A+∠B=180°,
∠A+∠C=180°,
则∠B=∠C.
等角的补角相等,
即:若∠A+∠B=180°,
∠D+∠C= 180°,
∠A=∠D,
则∠B=∠C.
同角的余角相等,
即:若∠A+∠B=90°,
∠A+∠C=90°,
则∠B=∠C.
等角的余角相等,
即:若∠A+∠B=90°,
∠D+∠C=90°,
∠A=∠D,
则∠B=∠C.
互为余角 互为补角
对应图形
数量关系
性 质
∠1+ ∠2 = 90 °
∠1+ ∠2 = 180 °
同角或等角的余角相等
同角或等角的补角相等
1
2
1
2
例题讲解
例3 如图①,直线AB与∠COD的两边OC,OD分别相交于点E,
F,∠1+∠2=180°.找出图中与∠2相等的角,并说明理由.
导引:已知∠1+∠2=180°,说明∠2是∠1的补角.根据同角
(或等角)的补角相等,找出图中∠1的其他补角和∠2的其他补角
的补角,便可确定与∠2相等的角.
解:如图②,因为∠1+∠3=180°,∠1+∠2=180°,
所以∠3=∠2.
因为∠1+∠4=180°,∠1+∠2=180°,
所以∠4=∠2.
因为∠2+∠5=180°,
∠6+∠5=180°,
所以∠2=∠6.
所以图中与∠2相等的角
有∠3,∠4,∠6.
1.定义:以正北、正南方向为基准,描述物体运动的方向,即正北、正南方向与物体运动方向的夹角为方位角.
注意事项:方位角在叙述时,一般先说南北,后说东西,
如南偏东30°.但与南北方向夹角为45°时,常简称为东北、东南、西北、西南,如南偏东45°,即为东南方向.
知识点3:方位角
东
西
北
南
O
正东:
正南:
正西:
正北:
西北方向:
西南方向:
东北方向:
东南方向:
射线 OA
A
B
C
D
45°
E
G
F
H
45°
八大方位
45°
45°
射线 OB
射线 OC
射线 OD
射线 OE
射线 OF
射线 OH
射线 OG
甲地
乙地
北
观测点
被观测点
如何表示在甲地观察乙地的方位角?
1.先找到观测点,然后画出方向指标;
甲地
乙地
北
视线
2.把观测点和被观测点用线段连接起来;
如何表示在甲地观察乙地的方位角?
甲地
乙地
北
方位角
如何表示在甲地观察乙地的方位角?
3.度量正北或正南方向的射线和视线之间的角度,就是所求方位角了。
例4 如图,货轮O在航行过程中,发现灯塔A在它南偏东60 的方向上.同时,在它北偏东40 、南偏西10 、西北(即北偏西45 )方向上又分别发现了客轮B、货轮C和海岛D.仿照表示灯塔方位的方法,画出表示客轮B、货轮C和海岛D方向的射线.
画法:以点O为顶点,表示正北方向的射线为角的一边,画40°的角,使它的另一边OB落在东和北之间.射线OB的方向就是北偏东40°,即客轮B所在的方向.同理,可以画出表示货轮C和海岛D方向的射线.
东
南
西
北
60°
● B
40°
10°
45°
C ●
● D
O
●
● A
随堂演练
1.一个角的余角是它的2倍,这个角的度数是( )
A.30° B.45° C.60° D.75°
A
2.如果一个角是56°,那么下列说法中正确的是( )
A.它的余角是44° B.它的补角是44°
C.它的余角是124° D.它的补角是124°
D
3. 如图,直线AB,CD交于点O,因为∠1+∠3=180°,∠2+∠3=180°,所以∠1=∠2的依据是( )
A.同角的余角相等
B.等角的余角相等
C.同角的补角相等
D.等角的补角相等
C
4. 如图,下面说法中不正确的是( )
A.射线OA表示北偏东30°
B.射线OB表示西北方向
C.射线OC表示西偏南80°
D.射线OD表示南偏东70°
C
5. ∠1 与 ∠2 互余,∠1 = (6x + 8)°,∠2 = (4x-8)°,
则∠1= ,∠2= .
62°
28°
6. 一个角的补角比它的余角的3倍小20°,求这个角的度数.
解:设这个角的度数为x°.
由题意,得180-x=3(90-x)-20,
解得x=35.
答:这个角的度数为35°.
7. 如图,D是直线EF上一点,∠CDE=90°,∠1=∠2,哪些角互为余角?哪些角互为补角?
解:∠1与∠ADC,∠1与∠BDC,∠2与∠BDC,∠2与∠ADC互为余角;
∠1与∠ADF,∠2与∠ADF,∠2与∠BDE,∠1与∠BDE,∠EDC与∠FDC互为补角.
课堂小结
余角和补角
余角
补角
两个角的和等于90
两个角的和等于180
定义
性质
同(等)角的余角相等
定义
性质
同(等)角的补角相等
方位角
正北、正南方向与物体运动方向的夹角为方位角
表示方向的角在航 行、测绘等工作中经常 用到
定义
应用
https://www.21cnjy.com/help/help_extract.php
