苏科版数学七年级下册 12.3 互逆命题 课件(共16张PPT)
文档属性
| 名称 | 苏科版数学七年级下册 12.3 互逆命题 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 170.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 17:04:22 | ||
图片预览






文档简介
(共16张PPT)
第12章
证明
12.3互逆命题
两直线平行,同位角相等.
条件
结论
同位角相等,两直线平行.
条件
结论
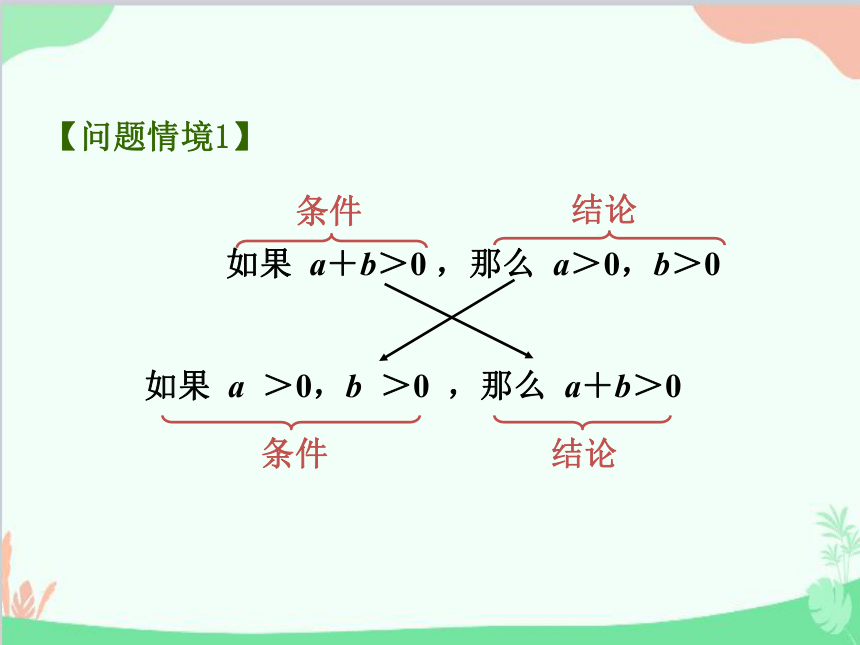
【问题情境1】
如果 a+b>0 ,那么 a>0,b>0
如果 a >0,b >0 ,那么 a+b>0
【问题情境1】
条件
结论
条件
结论
两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论又是第二个命题的条件,那么这两个命题叫做互逆命题.
其中一个命题是另一个命题的逆命题.
1.下列各组命题是否是互逆命题:
(1)“正方形的四个角都是直角”与“四个角都是直角的四边形是正方形”;
(2)“等于同一个角的两个角相等”与“如果两个角都等于同一个角,那么这两个角相等”;
(3)“对顶角相等”与“如果两个角相等,那么这两个角是对顶角”;
(4)“同位角相等,两直线平行”与“同位角不相等,两直线不平行” .
【试一试】
2 .说出下列命题的逆命题,并与同学交流.
(1)如果a2=b2,那么a=b;
(2)如果两个角是对顶角,那么它们的平分线组成一个平角;
(3)末位数字是5的数,能被5整除;
(4)锐角与钝角互为补角.
【试一试】
逆命题:如果a=b,那么a2=b2 .
逆命题:如果两个角的平分线组成一个平角,那么这两个角是对顶角.
逆命题:能被5整除的数的末位数字是5.
逆命题:互为补角的两个角一个是锐角一个是钝角.
在你已经学习过的命题中,举出两个命题,它们不仅是逆命题,而且都是真命题.
如图:
(1)如果AD∥EF,那么可以得到什么结论?
(2)如果∠EFC+∠C=180°,那么可以得到什么结论呢?
(3)证明AD∥EF,需要什么条件?证明EF∥BC 呢?
(4)证明AD∥EF∥BC,需要什么条件?
D
C
B
F
E
A
命题的证明
图形特殊的“位置关系”常常决定了图形具有特殊的“数量关系”;
反过来,图形特殊的“数量关系”常常决定了图形具有特殊的“位置关系”.
例1 证明:平行于同一条直线的两条直线平行.
已知:如图,直线a、b、c 中,b∥a, c∥a.
求证:b∥c .
a
b
c
证明:作直线a、b、c的截线d.
∵b∥a (已知),
∴∠2=∠1 (两直线平行,同位角相等),
∵c∥a (已知),
∴∠3=∠1 (两直线平行,同位角相等),
∴∠2=∠3 (等量代换),
∴b∥c (同位角相等,两直线平行).
d
1
2
3
例2 证明:直角三角形的两个锐角互余.
已知:如图,在△ABC 中,∠C=90°,
求证:∠A+∠B=90°.
证明:在△ABC 中, ∠A+∠B+∠C =180°
(三角形三个内角的和等于180°),
∴∠A +∠B = 180°- ∠C(等式性质),
∵ ∠C = 90°(已知),
∴∠A +∠B = 180°- 90°(等量代换),
∴ ∠A +∠B = 90°.
A
B
C
说出命题“直角三角形的两个锐角互余”的
逆命题.这个命题是真命题吗?为什么?
构造一个命题的逆命题,并证明这个命题是真命题,我们就能探索并获得一些新的数学结论.
这是一种逆向思考研究问题的方法.
【练习】
1. (1)如图,AB∥CD,AB、DE 相交于点G,
∠B=∠D. 在下列括号内填写推理的依据:
∵AB∥CD (已知),
∴∠EGA =∠D ( ).
又∵∠B =∠D (已知),
∴∠EGA =∠B( ),
∴DE∥BF ( ).
(2)上述推理中,应用了哪两个互逆的真命题?
C
D
A
B
E
G
F
2.(1)已知:如图,在直角三角形ABC 中∠ACB = 90°,D 是AB 上一点,且∠ACD =∠B .求证:CD⊥AB.
(2)你在(1)的证明过程中应用了哪两个互逆的真命题?
A
B
C
D
【小结】
通过今天的学习,你有哪些收获与体会,说出来和同学们分享.
【课后作业】
思考题(选做)
(1)已知:如图,在△ABC 中,点E 在AC上,
点F 在BC上,点D、G 在AB上,FG∥CD,
∠EDC =∠BFG .
求证:∠AED =∠ACB.
(2)你在(1)的证明过程中应用了哪两个互逆的真命题?
A
B
C
D
E
G
F
第12章
证明
12.3互逆命题
两直线平行,同位角相等.
条件
结论
同位角相等,两直线平行.
条件
结论
【问题情境1】
如果 a+b>0 ,那么 a>0,b>0
如果 a >0,b >0 ,那么 a+b>0
【问题情境1】
条件
结论
条件
结论
两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论又是第二个命题的条件,那么这两个命题叫做互逆命题.
其中一个命题是另一个命题的逆命题.
1.下列各组命题是否是互逆命题:
(1)“正方形的四个角都是直角”与“四个角都是直角的四边形是正方形”;
(2)“等于同一个角的两个角相等”与“如果两个角都等于同一个角,那么这两个角相等”;
(3)“对顶角相等”与“如果两个角相等,那么这两个角是对顶角”;
(4)“同位角相等,两直线平行”与“同位角不相等,两直线不平行” .
【试一试】
2 .说出下列命题的逆命题,并与同学交流.
(1)如果a2=b2,那么a=b;
(2)如果两个角是对顶角,那么它们的平分线组成一个平角;
(3)末位数字是5的数,能被5整除;
(4)锐角与钝角互为补角.
【试一试】
逆命题:如果a=b,那么a2=b2 .
逆命题:如果两个角的平分线组成一个平角,那么这两个角是对顶角.
逆命题:能被5整除的数的末位数字是5.
逆命题:互为补角的两个角一个是锐角一个是钝角.
在你已经学习过的命题中,举出两个命题,它们不仅是逆命题,而且都是真命题.
如图:
(1)如果AD∥EF,那么可以得到什么结论?
(2)如果∠EFC+∠C=180°,那么可以得到什么结论呢?
(3)证明AD∥EF,需要什么条件?证明EF∥BC 呢?
(4)证明AD∥EF∥BC,需要什么条件?
D
C
B
F
E
A
命题的证明
图形特殊的“位置关系”常常决定了图形具有特殊的“数量关系”;
反过来,图形特殊的“数量关系”常常决定了图形具有特殊的“位置关系”.
例1 证明:平行于同一条直线的两条直线平行.
已知:如图,直线a、b、c 中,b∥a, c∥a.
求证:b∥c .
a
b
c
证明:作直线a、b、c的截线d.
∵b∥a (已知),
∴∠2=∠1 (两直线平行,同位角相等),
∵c∥a (已知),
∴∠3=∠1 (两直线平行,同位角相等),
∴∠2=∠3 (等量代换),
∴b∥c (同位角相等,两直线平行).
d
1
2
3
例2 证明:直角三角形的两个锐角互余.
已知:如图,在△ABC 中,∠C=90°,
求证:∠A+∠B=90°.
证明:在△ABC 中, ∠A+∠B+∠C =180°
(三角形三个内角的和等于180°),
∴∠A +∠B = 180°- ∠C(等式性质),
∵ ∠C = 90°(已知),
∴∠A +∠B = 180°- 90°(等量代换),
∴ ∠A +∠B = 90°.
A
B
C
说出命题“直角三角形的两个锐角互余”的
逆命题.这个命题是真命题吗?为什么?
构造一个命题的逆命题,并证明这个命题是真命题,我们就能探索并获得一些新的数学结论.
这是一种逆向思考研究问题的方法.
【练习】
1. (1)如图,AB∥CD,AB、DE 相交于点G,
∠B=∠D. 在下列括号内填写推理的依据:
∵AB∥CD (已知),
∴∠EGA =∠D ( ).
又∵∠B =∠D (已知),
∴∠EGA =∠B( ),
∴DE∥BF ( ).
(2)上述推理中,应用了哪两个互逆的真命题?
C
D
A
B
E
G
F
2.(1)已知:如图,在直角三角形ABC 中∠ACB = 90°,D 是AB 上一点,且∠ACD =∠B .求证:CD⊥AB.
(2)你在(1)的证明过程中应用了哪两个互逆的真命题?
A
B
C
D
【小结】
通过今天的学习,你有哪些收获与体会,说出来和同学们分享.
【课后作业】
思考题(选做)
(1)已知:如图,在△ABC 中,点E 在AC上,
点F 在BC上,点D、G 在AB上,FG∥CD,
∠EDC =∠BFG .
求证:∠AED =∠ACB.
(2)你在(1)的证明过程中应用了哪两个互逆的真命题?
A
B
C
D
E
G
F
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
