苏科版数学七年级下册 9.2 单项式乘多项式 课件(共17张PPT)
文档属性
| 名称 | 苏科版数学七年级下册 9.2 单项式乘多项式 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 177.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 17:11:31 | ||
图片预览





文档简介
(共17张PPT)
第9章
整式乘法与因式分解
9.2单项式乘多项式
1.单项式与单项式相乘法则:
(1)各单项式的系数相乘;
(2)相同字母的幂分别相乘;
(3)只在一个单项式因式里含有的字母, 连同它的指数作为积的一个因式.
2. 什么叫多项式
几个单项式的和叫做多项式。
在多项式中,每个单项式叫做多项式的项。
3. 什么叫多项式的项
说出多项式2x2+3x-1的项和各项系数
温故知新
a
b
c
d
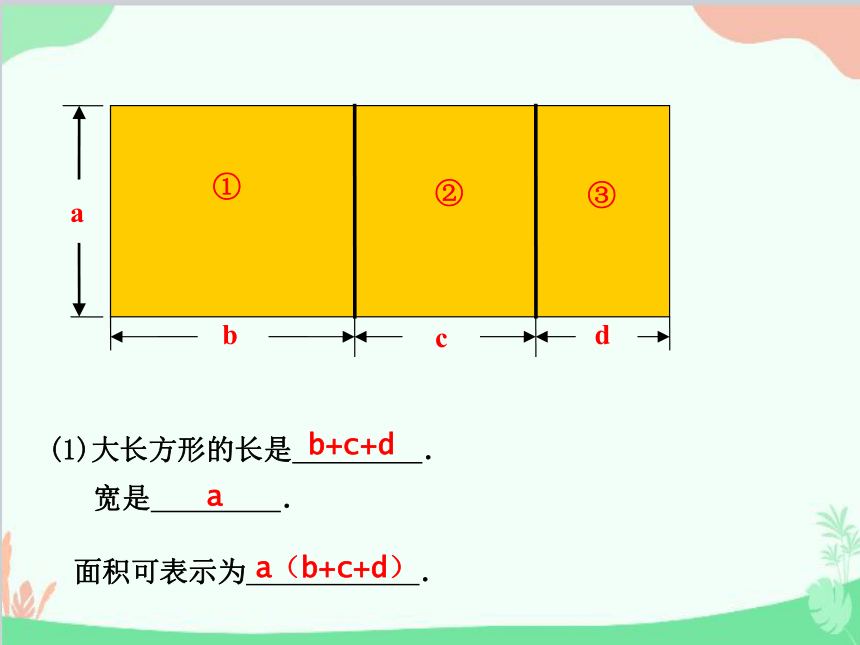
(1)大长方形的长是 .
①
②
③
b+c+d
宽是 .
面积可表示为 .
a
a(b+c+d)
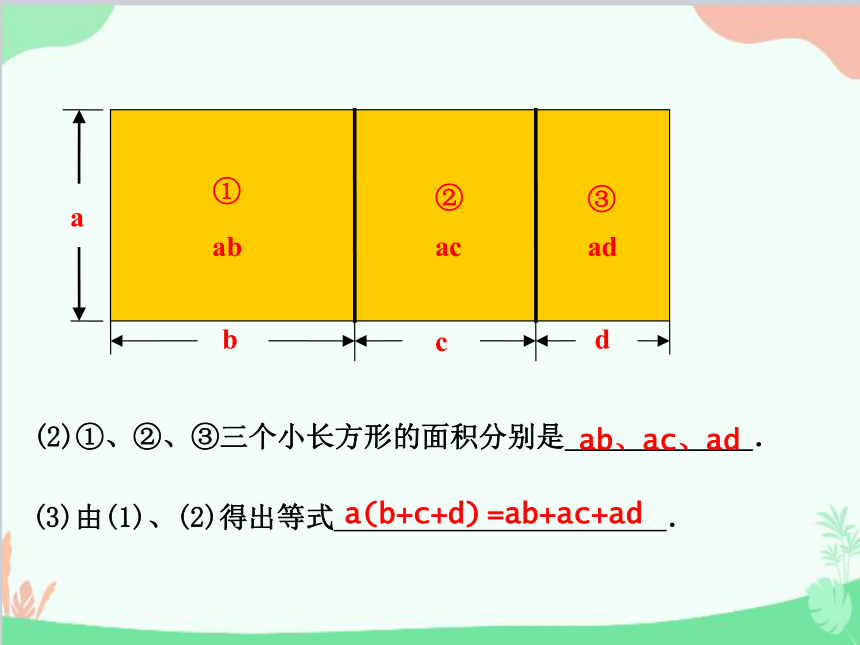
(2)①、②、③三个小长方形的面积分别是_____________.
(3)由(1)、(2)得出等式_______________________.
ab、ac、ad
a(b+c+d)
=ab+ac+ad
a
b
c
d
①
②
③
ab
ac
ad
做一做
计算下列各式,并说明理由
(1) a(5a+3b)
(2) (x-2y).2x
怎样叙述单项式与多项式相乘的法则
a(b+c+d)=ab+ac+ad
(a、b、c d都是单项式)
单项式与多项式相乘法则
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加
a(b+c+d)=ab+ac+ad
(a、b、c 、d都是单项式)
例1 计算:
1、(-3x2)·(4x-3)
2、( ab2-3ab). ab
3
4
1
3
3、(-2a) (2a2-3a+1)
单项式与多项式相乘时,分三步:
①按乘法分配律把乘积写成单项式与单项式乘积的代数和的形式;
②单项式的乘法运算;
③再把所得的积相加.
一分配
二相乘
三相加
几点注意
1.单项式乘多项式的结果仍是多项式,积的项数与原多项式的项数相同。
2.单项式分别与多项式的每一项相乘时,要注意积的各项符号的确定:同号相乘得正,异号相乘得负.
3.不要出现漏乘现象,运算要有顺序。
例2. 如图,一长方形地块用来建造住宅、广场、商厦.求这块地的面积.
巩固练习
一.判断
×
×
1.m(a+b+c+d)=ma+b+c+d( )
( )
3.(-2x) (ax+b-3)=-2ax2-2bx-6x( )
×
1.单项式与多项式相乘,就是用单项式去乘
多项式的________,再把所得的积________
二.填空
2.4(a-b+1)=____________
每一项
相加
4a-4b+4
3.3x(2x-y2)=____________
6x2-3xy2
4.-3x(2x-5y+6z)=_________________
-6x2+15xy-18xz
5.(-2a2)2(-a-2b+c)=_________________
-4a5-8a4b+4a4c
三.选择
下列计算错误的是( )
(A)5x(2x2-y)=10x3-5xy
(B)-3xa+b 4xa-b=-12x2a
(C)2a2b 4ab2=8a3b3
(D)(-xn-1y2) (-xym)2=xnym+2
D
(-2ab)3(5a2b–2b3)
解:原式=(-8a3b3)(5a2b–2b3)
=(-8a3b3)·(5a2b)+(-8a3b3)·(-2b3)
=-40a5b4+16a3b6
说明:先进行乘方运算,再进行单项式与多项式的乘法运算。
能力提升题
-2a2·(ab+b2)-5a(a2b-ab2)
解:原式=-2a3b-2a2b2-5a3b+5a2b2
=-2a3b-2a2b2-5a3b+5a2b2
注意:
1.将-2a2与-5a的“-”看成性质符号
2.单项式与多项式相乘的结果中,应将同类项合并。
=-7a3b+3a2b2
能力提升题
yn(yn +9y-12)–3(3yn+1-4yn),
其中y=-3,n=2.
解:yn(yn + 9y-12)–3(3yn+1-4yn)
=y2n+9yn+1-12yn–9yn+1+12yn
=y2n
当y=-3,n=2时,
原式=(-3)2×2=(-3)4=81
能力提升题
第9章
整式乘法与因式分解
9.2单项式乘多项式
1.单项式与单项式相乘法则:
(1)各单项式的系数相乘;
(2)相同字母的幂分别相乘;
(3)只在一个单项式因式里含有的字母, 连同它的指数作为积的一个因式.
2. 什么叫多项式
几个单项式的和叫做多项式。
在多项式中,每个单项式叫做多项式的项。
3. 什么叫多项式的项
说出多项式2x2+3x-1的项和各项系数
温故知新
a
b
c
d
(1)大长方形的长是 .
①
②
③
b+c+d
宽是 .
面积可表示为 .
a
a(b+c+d)
(2)①、②、③三个小长方形的面积分别是_____________.
(3)由(1)、(2)得出等式_______________________.
ab、ac、ad
a(b+c+d)
=ab+ac+ad
a
b
c
d
①
②
③
ab
ac
ad
做一做
计算下列各式,并说明理由
(1) a(5a+3b)
(2) (x-2y).2x
怎样叙述单项式与多项式相乘的法则
a(b+c+d)=ab+ac+ad
(a、b、c d都是单项式)
单项式与多项式相乘法则
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加
a(b+c+d)=ab+ac+ad
(a、b、c 、d都是单项式)
例1 计算:
1、(-3x2)·(4x-3)
2、( ab2-3ab). ab
3
4
1
3
3、(-2a) (2a2-3a+1)
单项式与多项式相乘时,分三步:
①按乘法分配律把乘积写成单项式与单项式乘积的代数和的形式;
②单项式的乘法运算;
③再把所得的积相加.
一分配
二相乘
三相加
几点注意
1.单项式乘多项式的结果仍是多项式,积的项数与原多项式的项数相同。
2.单项式分别与多项式的每一项相乘时,要注意积的各项符号的确定:同号相乘得正,异号相乘得负.
3.不要出现漏乘现象,运算要有顺序。
例2. 如图,一长方形地块用来建造住宅、广场、商厦.求这块地的面积.
巩固练习
一.判断
×
×
1.m(a+b+c+d)=ma+b+c+d( )
( )
3.(-2x) (ax+b-3)=-2ax2-2bx-6x( )
×
1.单项式与多项式相乘,就是用单项式去乘
多项式的________,再把所得的积________
二.填空
2.4(a-b+1)=____________
每一项
相加
4a-4b+4
3.3x(2x-y2)=____________
6x2-3xy2
4.-3x(2x-5y+6z)=_________________
-6x2+15xy-18xz
5.(-2a2)2(-a-2b+c)=_________________
-4a5-8a4b+4a4c
三.选择
下列计算错误的是( )
(A)5x(2x2-y)=10x3-5xy
(B)-3xa+b 4xa-b=-12x2a
(C)2a2b 4ab2=8a3b3
(D)(-xn-1y2) (-xym)2=xnym+2
D
(-2ab)3(5a2b–2b3)
解:原式=(-8a3b3)(5a2b–2b3)
=(-8a3b3)·(5a2b)+(-8a3b3)·(-2b3)
=-40a5b4+16a3b6
说明:先进行乘方运算,再进行单项式与多项式的乘法运算。
能力提升题
-2a2·(ab+b2)-5a(a2b-ab2)
解:原式=-2a3b-2a2b2-5a3b+5a2b2
=-2a3b-2a2b2-5a3b+5a2b2
注意:
1.将-2a2与-5a的“-”看成性质符号
2.单项式与多项式相乘的结果中,应将同类项合并。
=-7a3b+3a2b2
能力提升题
yn(yn +9y-12)–3(3yn+1-4yn),
其中y=-3,n=2.
解:yn(yn + 9y-12)–3(3yn+1-4yn)
=y2n+9yn+1-12yn–9yn+1+12yn
=y2n
当y=-3,n=2时,
原式=(-3)2×2=(-3)4=81
能力提升题
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
