2021-2022学年鲁教五四新版八年级上册数学期中复习试卷(word解析版)
文档属性
| 名称 | 2021-2022学年鲁教五四新版八年级上册数学期中复习试卷(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 249.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-08 06:39:41 | ||
图片预览




文档简介
2021-2022学年鲁教五四新版八年级上册数学期中复习试卷
一.选择题(共10小题,满分30分,每小题3分)
1.若x2﹣6x+a=(bx﹣3)2,则a,b的值分别为( )
A.9,1 B.﹣9,1 C.﹣9,﹣1 D.9,﹣1
2.在一次射击练习中,王明的射击成绩(单位:环)分别是8,9,9,9,10,下列关于这组数据的说法中错误的是( )
A.平均数9 B.中位数9 C.众数9 D.方差9
3.下列式子直接能用完全平方公式进行因式分解的是( )
A.16a2+8a+1 B.a2﹣3a+9 C.4a2+4a﹣1 D.a2﹣8a﹣16
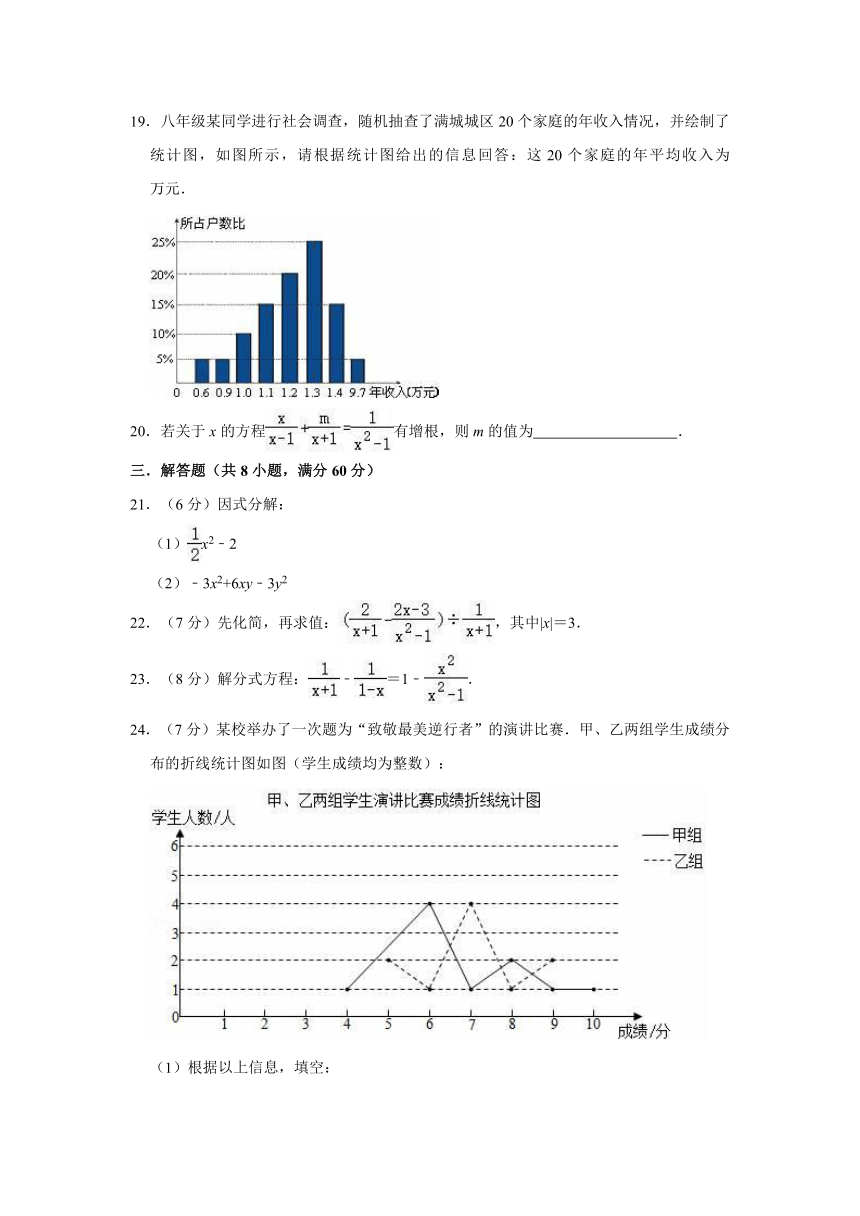
4.下列说法正确的是( )
A.的算术平方根是9
B.一组数据的极差、方差或标准差越小,这组数据就越稳定
C.三角形的一个外角等于它的两个内角之和
D.立方根等于自身的数有1和0
5.已知水的密度为1,冰的密度为0.9.现将1个单位体积的水结成冰后的体积增长率为p,1个单位体积的冰溶成水后的体积的下降率为q,则p、q的大小关系为( )
A.p>q B.p=q C.p<q D.不能确定
6.已知x2﹣mx+9是某个整式的平方的展开式,则m的值为( )
A.3 B.±3 C.6 D.±6
7.÷等于( )
A. B. b2x
C.﹣ D.﹣
8.分式是刻画数量关系和变化规律的一类重要的代数式,我们学习了分式的概念,基本性质和运算.回顾学习分式的过程,常常是先回顾分数的概念、分数的基本性质和分数的运算法则,然后推广得到分式的概念、分式的基本性质和分式的运算法则.这种研究方法主要体现的数学思想是( )
A.归纳思想 B.类比思想
C.数学抽象 D.数形结合思想
9.如表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数与方差:
甲 乙 丙 丁
平均数 375 350 375 350
方差s2 12.5 13.5 2.4 5.4
要从中选择一名成绩好又发挥稳定的运动员参加决赛,最合适的是( )
A.甲 B.乙 C.丙 D.丁
10.已知x2+y2+2x﹣6y+10=0,则x+y=( )
A.2 B.﹣2 C.4 D.﹣4
二.填空题(共10小题,满分30分,每小题3分)
11.分解因式:(a+2b)2﹣22(a+2b)+121= .
12.现有一张边长为a的大正方形卡片和三张边长为b的小正方形卡片(a<b<a),如图1;取出两张小正方形卡片放入大正方形卡片内拼成的图案如图2;再重新用三张小正方形卡片放入大正方形卡片内拼成的图案如图3.则图3中阴影部分的面积为 (用含有a,b的代数式表示);已知图3中的阴影部分的面积比图2中的阴影部分的面积大2ab﹣15,则小正方形卡片的面积是 .
13.若9x2﹣kxy+4y2是一个完全平方式,则k的值是 .
14.若关于x的分式方程=2a无解,则a的值为 .
15.某选手在比赛中的成绩(单位:分)分别是90,87,92,88,93,方差是5.2(单位:分2),如果去掉一个最高分和一个最低分,那么该选手成绩的方差会 (填“变大”、“变小”、“不变”或“不能确定”).
16.若分式的值为0,则x的值为 .
17.已知x2+y2+2x﹣4y+5=0,则x+y= .
18.在代数式中,分式有 个.
19.八年级某同学进行社会调查,随机抽查了满城城区20个家庭的年收入情况,并绘制了统计图,如图所示,请根据统计图给出的信息回答:这20个家庭的年平均收入为 万元.
20.若关于x的方程有增根,则m的值为 .
三.解答题(共8小题,满分60分)
21.(6分)因式分解:
(1)x2﹣2
(2)﹣3x2+6xy﹣3y2
22.(7分)先化简,再求值:,其中|x|=3.
23.(8分)解分式方程:﹣=1﹣.
24.(7分)某校举办了一次题为“致敬最美逆行者”的演讲比赛.甲、乙两组学生成绩分布的折线统计图如图(学生成绩均为整数):
(1)根据以上信息,填空:
组别 平均数/分 中位数/分 方差/分2
甲 7 2.8
乙 7
(2)如果学校准备选派其中一组参加区级比赛,你认为选派哪一组参赛更好?为什么?
25.(8分)已知a+b=7,ab=10.求a2+b2与a2﹣b2的值.
26.(9分)为更好地开展体育运动,增加学生体质,学校准备在运动会前购买一批运动鞋,供学生借用.七(2)班为配合学校工作,从全校各个年级共随机抽查了38名同学的鞋号,具体数据如下:
35 37 36 35 37 36 37 38
36 37 37 35 35 34 34 35
35 36 37 36 38 39 37 35
36 35 36 37 33 34 40 36
35 34 35 36 37 36
整理上面的数据,看看穿不同鞋号的同学各有多少,他们各占调查总人数的百分之几,请你对学校购鞋提出建议.
27.(9分)甲乙二人做某种机械零件,已知甲每小时比乙多做6个,甲做90个所用时间与乙做60个所用时间相等.求甲、乙每小时各做多少个零件?
28.(6分)观察下列方程,回答问题
①的解为x=0.
②的解为x=1.
③的解为x=2.
④的解为x=3.
(1)请直接写出第5个方程及它的解;
(2)请你写出第n(n为正整数)个方程,并求出它的解.(写出解答过程)
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:(bx﹣3)2=b2x2﹣6bx+9,
∵x2﹣6x+a=(bx﹣3)2,
∴﹣6b=﹣6,a=9,
解得a=9,b=1,
故选:A.
2.解:平均数=(8+9+9+9+10)÷5=9,
中位数是9,众数是9,
方差S2= [(8﹣9)2+(9﹣9)2+(9﹣9)2+(9﹣9)2+(10﹣9)2]=.
所以D错误.
故选:D.
3.解:A、16a2+8a+1=(4a+1)2,符合完全平方公式,故本选项正确;
B、a2﹣3a+9中3不是a与3这两个数(或式)的积的2倍,不符合完全平方公式分解因式的式子特点,故此选项错误;
C、4a2+4a﹣1中的常数项不是平方的形式,不符合完全平方公式分解因式的式子特点,故此选项错误;
D、a2﹣8a﹣16中的常数项不是平方的形式,不符合完全平方公式分解因式的式子特点,故此选项错误;
故选:A.
4.解:A、的算术平方根是3,故本选项错误;
B、一组数据的极差、方差或标准差越小,这组数据就越稳定,正确;
C、三角形的一个外角等于与它不相邻的两个内角之和,故本选项错误;
D、立方根等于它本身的数是﹣1、0、1,故本选项错误;
故选:B.
5.冰水转化时质量不变,设质量为a.那么P===,Q===.则p>q.
故选:A.
6.解:∵x2﹣mx+9=x2﹣mx+32是某个整式的平方的展开式,
∴﹣m=±6,
解得:m=±6.
故选:D.
7.解:原式=﹣
=﹣
=﹣.
故选:C.
8.解:我们学习了分式的概念,基本性质和运算.回顾学习分式的过程,常常是先回顾分数的概念、分数的基本性质和分数的运算法则,然后推广得到分式的概念、分式的基本性质和分式的运算法则.这种研究方法主要体现的数学思想是类比思想,
故选:B.
9.解:∵乙和丁的平均数最小,
∴从甲和丙中选择一人参加比赛,
∵丙的方差最小,
∴选择丙参赛,
故选:C.
10.解:∵x2+y2+2x﹣6y+10=0,
∴x2+2x+1+y2﹣6y+9=0
即:(x+1)2+(y﹣3)2=0
解得:x=﹣1,y=3
∴x+y=﹣1+3=2,
故选:A.
二.填空题(共10小题,满分30分,每小题3分)
11.解:原式=(a+2b)2﹣2×11×(a+2b)+112=(a+2b﹣11)2,
故答案为(a+2b﹣11)2.
12.解:图2中阴影部分是正方形,它的边长是(2b﹣a),
所以它的面积就是(2b﹣a)2.
图3中阴影部分可以上下拼合到一起,其边长就是(a﹣b),
所以它的面积就可以表示为:(a﹣b)2.
又因为图3中的阴影部分的面积比图2中的阴影部分的面积大2ab﹣15,
所以可得:
(2b﹣a)2+2ab﹣15=(a﹣b)2,
4b2﹣4ab+a2+2ab﹣15=a2+b2﹣2ab,
3b2=15,
b2=5,
故小正方形的面积是5.
13.解:中间一项为加上或减去3x和2y积的2倍.
故k=±12.
14.解:=2a,
去分母得:x﹣2a=2a(x﹣3),
整理得:(1﹣2a)x=﹣4a,
当1﹣2a=0时,方程无解,故a=0.5;
当1﹣2a≠0时,x==3时,分式方程无解,则a=1.5,
则a的值为0.5或1.5.
故答案为:0.5或1.5.
15.解:去掉一个最高分和一个最低分后为88,90,92,
平均数为=90,
方差为 [(88﹣90)2+(90﹣90)2+(92﹣90)2]=≈2.67(分2),
因为5.2>2.67,
所以方差变小了,
故答案为:变小.
16.解:∵分式的值为0,
∴|x|﹣5=0且2x﹣10≠0,
解得:x=﹣5.
故答案为:﹣5.
17.解:∵x2+y2+2x﹣4y+5=0,
∴(x+1)2+(y﹣2)2=0,
∴x+1=0,y﹣2=0,
∴x=﹣1,y=2,
∴x+y=1.
故答案为:1.
18.解:,的分母中含有字母,是分式.
故答案是:2.
19.解:平均收入=0.6×5%+0.9×5%+1×10%+1.1×15%+1.2×20%+1.3×25%+1.4×15%+9.7×5%=1.6(万元).
故填1.67.
20.解:方程两边同时乘以(x+1)(x﹣1),得:
x(x+1)+m(x﹣1)=1,
整理得:x2+(m+1)x﹣1﹣m=0 ①,
∵分式方程有增根,
即(x+1)(x﹣1)=0,得:x=﹣1或1.
当x=﹣1时,代入①方程中,得m=;
当x=1时,代入①方程中,m无解.
故答案为:.
三.解答题(共8小题,满分60分)
21.解:(1)原式=(x2﹣4)=(x+2)(x﹣2);
(2)原式=﹣3(x2﹣2xy+y2)=﹣3(x﹣y)2.
22.解:
=
=
=,
∵|x|=3,
∴x=±3,
∴当x=3时,原式==;
当x=﹣3时,原式==﹣.
23.解:去分母得:x﹣1+x+1=x2﹣1﹣x2,
移项,合并同类项得2x=﹣1,
系数化为1得x=﹣,
检验:把x=﹣代入x2﹣1≠0,
所以原方程的解为x=﹣.
24.解:(1)甲组:4分的有1人,6分有4人,7分的有1人,8分的有2人,9分的有1人,10分的有1人,
把这些数从小大排列为4、6、6、6、6、7、8、8、9、10,则中位数是:=6.5(分),
乙组:5分的有2人,6分有1人,7分的有4人,8分的有1人,9分的有2人,
平均数是:(5+5+6+7+7+7+7+8+9+9)=7(分),
乙组的方差是: [2×(5﹣7)2+(6﹣7)2+4×(7﹣7)2+(8﹣7)2+2×(9﹣7)2]=1.8(分2).
故答案为:6.5,7,1.8;
(2)因为乙组的中位数均高于甲组,且乙组的方差小于甲组的方差,比甲组的成绩稳定,所以应派乙组参赛更好.
25.解:∵a+b=7,ab=10,
∴a2+b2=(a+b)2﹣2ab=49﹣2×10=29;
∵a+b=7,ab=10,
∴(a﹣b)2=(a+b)2﹣4ab=49﹣4×10=9,
∴a﹣b=±3,
∴a2﹣b2=(a+b)(a﹣b)=7×3=21,
或a2﹣b2=(a+b)(a﹣b)=7×(﹣3)=﹣21.
综上所述a2+b2的值是29,a2﹣b2的值是21或﹣21.
26.解:将这38位同学所穿鞋号进行统计,并计算所占调查人数的百分比,如下表:
通过表格中的数据,可以得出,鞋号为35、36、27号的鞋所占的比例较高,
因此在学校购鞋时,应注意这三个号码应多买,这三个号码的鞋约占总数的75%.
27.解:设乙每小时做x个零件,甲每小时做(x+6)个零件,
根据题意得:,
解得:x=12,
经检验,x=12是原方程的解,且符合题意,
∴x+6=18.
答:乙每小时做12个零件,甲每小时做18个零件.
28.解:(1)根据题意得:第⑤个方程: +1=,解为x=4;
(2)写出第n个方程: +1=,
方程两边同时乘以(x+1),得:n+(x+1)=2n,
解得:x=n﹣1,
经检验:x=n﹣1是原方程的解,
∴原方程的解为:x=n﹣1.
一.选择题(共10小题,满分30分,每小题3分)
1.若x2﹣6x+a=(bx﹣3)2,则a,b的值分别为( )
A.9,1 B.﹣9,1 C.﹣9,﹣1 D.9,﹣1
2.在一次射击练习中,王明的射击成绩(单位:环)分别是8,9,9,9,10,下列关于这组数据的说法中错误的是( )
A.平均数9 B.中位数9 C.众数9 D.方差9
3.下列式子直接能用完全平方公式进行因式分解的是( )
A.16a2+8a+1 B.a2﹣3a+9 C.4a2+4a﹣1 D.a2﹣8a﹣16
4.下列说法正确的是( )
A.的算术平方根是9
B.一组数据的极差、方差或标准差越小,这组数据就越稳定
C.三角形的一个外角等于它的两个内角之和
D.立方根等于自身的数有1和0
5.已知水的密度为1,冰的密度为0.9.现将1个单位体积的水结成冰后的体积增长率为p,1个单位体积的冰溶成水后的体积的下降率为q,则p、q的大小关系为( )
A.p>q B.p=q C.p<q D.不能确定
6.已知x2﹣mx+9是某个整式的平方的展开式,则m的值为( )
A.3 B.±3 C.6 D.±6
7.÷等于( )
A. B. b2x
C.﹣ D.﹣
8.分式是刻画数量关系和变化规律的一类重要的代数式,我们学习了分式的概念,基本性质和运算.回顾学习分式的过程,常常是先回顾分数的概念、分数的基本性质和分数的运算法则,然后推广得到分式的概念、分式的基本性质和分式的运算法则.这种研究方法主要体现的数学思想是( )
A.归纳思想 B.类比思想
C.数学抽象 D.数形结合思想
9.如表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数与方差:
甲 乙 丙 丁
平均数 375 350 375 350
方差s2 12.5 13.5 2.4 5.4
要从中选择一名成绩好又发挥稳定的运动员参加决赛,最合适的是( )
A.甲 B.乙 C.丙 D.丁
10.已知x2+y2+2x﹣6y+10=0,则x+y=( )
A.2 B.﹣2 C.4 D.﹣4
二.填空题(共10小题,满分30分,每小题3分)
11.分解因式:(a+2b)2﹣22(a+2b)+121= .
12.现有一张边长为a的大正方形卡片和三张边长为b的小正方形卡片(a<b<a),如图1;取出两张小正方形卡片放入大正方形卡片内拼成的图案如图2;再重新用三张小正方形卡片放入大正方形卡片内拼成的图案如图3.则图3中阴影部分的面积为 (用含有a,b的代数式表示);已知图3中的阴影部分的面积比图2中的阴影部分的面积大2ab﹣15,则小正方形卡片的面积是 .
13.若9x2﹣kxy+4y2是一个完全平方式,则k的值是 .
14.若关于x的分式方程=2a无解,则a的值为 .
15.某选手在比赛中的成绩(单位:分)分别是90,87,92,88,93,方差是5.2(单位:分2),如果去掉一个最高分和一个最低分,那么该选手成绩的方差会 (填“变大”、“变小”、“不变”或“不能确定”).
16.若分式的值为0,则x的值为 .
17.已知x2+y2+2x﹣4y+5=0,则x+y= .
18.在代数式中,分式有 个.
19.八年级某同学进行社会调查,随机抽查了满城城区20个家庭的年收入情况,并绘制了统计图,如图所示,请根据统计图给出的信息回答:这20个家庭的年平均收入为 万元.
20.若关于x的方程有增根,则m的值为 .
三.解答题(共8小题,满分60分)
21.(6分)因式分解:
(1)x2﹣2
(2)﹣3x2+6xy﹣3y2
22.(7分)先化简,再求值:,其中|x|=3.
23.(8分)解分式方程:﹣=1﹣.
24.(7分)某校举办了一次题为“致敬最美逆行者”的演讲比赛.甲、乙两组学生成绩分布的折线统计图如图(学生成绩均为整数):
(1)根据以上信息,填空:
组别 平均数/分 中位数/分 方差/分2
甲 7 2.8
乙 7
(2)如果学校准备选派其中一组参加区级比赛,你认为选派哪一组参赛更好?为什么?
25.(8分)已知a+b=7,ab=10.求a2+b2与a2﹣b2的值.
26.(9分)为更好地开展体育运动,增加学生体质,学校准备在运动会前购买一批运动鞋,供学生借用.七(2)班为配合学校工作,从全校各个年级共随机抽查了38名同学的鞋号,具体数据如下:
35 37 36 35 37 36 37 38
36 37 37 35 35 34 34 35
35 36 37 36 38 39 37 35
36 35 36 37 33 34 40 36
35 34 35 36 37 36
整理上面的数据,看看穿不同鞋号的同学各有多少,他们各占调查总人数的百分之几,请你对学校购鞋提出建议.
27.(9分)甲乙二人做某种机械零件,已知甲每小时比乙多做6个,甲做90个所用时间与乙做60个所用时间相等.求甲、乙每小时各做多少个零件?
28.(6分)观察下列方程,回答问题
①的解为x=0.
②的解为x=1.
③的解为x=2.
④的解为x=3.
(1)请直接写出第5个方程及它的解;
(2)请你写出第n(n为正整数)个方程,并求出它的解.(写出解答过程)
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:(bx﹣3)2=b2x2﹣6bx+9,
∵x2﹣6x+a=(bx﹣3)2,
∴﹣6b=﹣6,a=9,
解得a=9,b=1,
故选:A.
2.解:平均数=(8+9+9+9+10)÷5=9,
中位数是9,众数是9,
方差S2= [(8﹣9)2+(9﹣9)2+(9﹣9)2+(9﹣9)2+(10﹣9)2]=.
所以D错误.
故选:D.
3.解:A、16a2+8a+1=(4a+1)2,符合完全平方公式,故本选项正确;
B、a2﹣3a+9中3不是a与3这两个数(或式)的积的2倍,不符合完全平方公式分解因式的式子特点,故此选项错误;
C、4a2+4a﹣1中的常数项不是平方的形式,不符合完全平方公式分解因式的式子特点,故此选项错误;
D、a2﹣8a﹣16中的常数项不是平方的形式,不符合完全平方公式分解因式的式子特点,故此选项错误;
故选:A.
4.解:A、的算术平方根是3,故本选项错误;
B、一组数据的极差、方差或标准差越小,这组数据就越稳定,正确;
C、三角形的一个外角等于与它不相邻的两个内角之和,故本选项错误;
D、立方根等于它本身的数是﹣1、0、1,故本选项错误;
故选:B.
5.冰水转化时质量不变,设质量为a.那么P===,Q===.则p>q.
故选:A.
6.解:∵x2﹣mx+9=x2﹣mx+32是某个整式的平方的展开式,
∴﹣m=±6,
解得:m=±6.
故选:D.
7.解:原式=﹣
=﹣
=﹣.
故选:C.
8.解:我们学习了分式的概念,基本性质和运算.回顾学习分式的过程,常常是先回顾分数的概念、分数的基本性质和分数的运算法则,然后推广得到分式的概念、分式的基本性质和分式的运算法则.这种研究方法主要体现的数学思想是类比思想,
故选:B.
9.解:∵乙和丁的平均数最小,
∴从甲和丙中选择一人参加比赛,
∵丙的方差最小,
∴选择丙参赛,
故选:C.
10.解:∵x2+y2+2x﹣6y+10=0,
∴x2+2x+1+y2﹣6y+9=0
即:(x+1)2+(y﹣3)2=0
解得:x=﹣1,y=3
∴x+y=﹣1+3=2,
故选:A.
二.填空题(共10小题,满分30分,每小题3分)
11.解:原式=(a+2b)2﹣2×11×(a+2b)+112=(a+2b﹣11)2,
故答案为(a+2b﹣11)2.
12.解:图2中阴影部分是正方形,它的边长是(2b﹣a),
所以它的面积就是(2b﹣a)2.
图3中阴影部分可以上下拼合到一起,其边长就是(a﹣b),
所以它的面积就可以表示为:(a﹣b)2.
又因为图3中的阴影部分的面积比图2中的阴影部分的面积大2ab﹣15,
所以可得:
(2b﹣a)2+2ab﹣15=(a﹣b)2,
4b2﹣4ab+a2+2ab﹣15=a2+b2﹣2ab,
3b2=15,
b2=5,
故小正方形的面积是5.
13.解:中间一项为加上或减去3x和2y积的2倍.
故k=±12.
14.解:=2a,
去分母得:x﹣2a=2a(x﹣3),
整理得:(1﹣2a)x=﹣4a,
当1﹣2a=0时,方程无解,故a=0.5;
当1﹣2a≠0时,x==3时,分式方程无解,则a=1.5,
则a的值为0.5或1.5.
故答案为:0.5或1.5.
15.解:去掉一个最高分和一个最低分后为88,90,92,
平均数为=90,
方差为 [(88﹣90)2+(90﹣90)2+(92﹣90)2]=≈2.67(分2),
因为5.2>2.67,
所以方差变小了,
故答案为:变小.
16.解:∵分式的值为0,
∴|x|﹣5=0且2x﹣10≠0,
解得:x=﹣5.
故答案为:﹣5.
17.解:∵x2+y2+2x﹣4y+5=0,
∴(x+1)2+(y﹣2)2=0,
∴x+1=0,y﹣2=0,
∴x=﹣1,y=2,
∴x+y=1.
故答案为:1.
18.解:,的分母中含有字母,是分式.
故答案是:2.
19.解:平均收入=0.6×5%+0.9×5%+1×10%+1.1×15%+1.2×20%+1.3×25%+1.4×15%+9.7×5%=1.6(万元).
故填1.67.
20.解:方程两边同时乘以(x+1)(x﹣1),得:
x(x+1)+m(x﹣1)=1,
整理得:x2+(m+1)x﹣1﹣m=0 ①,
∵分式方程有增根,
即(x+1)(x﹣1)=0,得:x=﹣1或1.
当x=﹣1时,代入①方程中,得m=;
当x=1时,代入①方程中,m无解.
故答案为:.
三.解答题(共8小题,满分60分)
21.解:(1)原式=(x2﹣4)=(x+2)(x﹣2);
(2)原式=﹣3(x2﹣2xy+y2)=﹣3(x﹣y)2.
22.解:
=
=
=,
∵|x|=3,
∴x=±3,
∴当x=3时,原式==;
当x=﹣3时,原式==﹣.
23.解:去分母得:x﹣1+x+1=x2﹣1﹣x2,
移项,合并同类项得2x=﹣1,
系数化为1得x=﹣,
检验:把x=﹣代入x2﹣1≠0,
所以原方程的解为x=﹣.
24.解:(1)甲组:4分的有1人,6分有4人,7分的有1人,8分的有2人,9分的有1人,10分的有1人,
把这些数从小大排列为4、6、6、6、6、7、8、8、9、10,则中位数是:=6.5(分),
乙组:5分的有2人,6分有1人,7分的有4人,8分的有1人,9分的有2人,
平均数是:(5+5+6+7+7+7+7+8+9+9)=7(分),
乙组的方差是: [2×(5﹣7)2+(6﹣7)2+4×(7﹣7)2+(8﹣7)2+2×(9﹣7)2]=1.8(分2).
故答案为:6.5,7,1.8;
(2)因为乙组的中位数均高于甲组,且乙组的方差小于甲组的方差,比甲组的成绩稳定,所以应派乙组参赛更好.
25.解:∵a+b=7,ab=10,
∴a2+b2=(a+b)2﹣2ab=49﹣2×10=29;
∵a+b=7,ab=10,
∴(a﹣b)2=(a+b)2﹣4ab=49﹣4×10=9,
∴a﹣b=±3,
∴a2﹣b2=(a+b)(a﹣b)=7×3=21,
或a2﹣b2=(a+b)(a﹣b)=7×(﹣3)=﹣21.
综上所述a2+b2的值是29,a2﹣b2的值是21或﹣21.
26.解:将这38位同学所穿鞋号进行统计,并计算所占调查人数的百分比,如下表:
通过表格中的数据,可以得出,鞋号为35、36、27号的鞋所占的比例较高,
因此在学校购鞋时,应注意这三个号码应多买,这三个号码的鞋约占总数的75%.
27.解:设乙每小时做x个零件,甲每小时做(x+6)个零件,
根据题意得:,
解得:x=12,
经检验,x=12是原方程的解,且符合题意,
∴x+6=18.
答:乙每小时做12个零件,甲每小时做18个零件.
28.解:(1)根据题意得:第⑤个方程: +1=,解为x=4;
(2)写出第n个方程: +1=,
方程两边同时乘以(x+1),得:n+(x+1)=2n,
解得:x=n﹣1,
经检验:x=n﹣1是原方程的解,
∴原方程的解为:x=n﹣1.
同课章节目录
