2021-2022学年沪教新版八年级上册数学期中复习试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年沪教新版八年级上册数学期中复习试卷(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 304.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-08 07:34:22 | ||
图片预览




文档简介
2021-2022学年沪教新版八年级上册数学期中复习试卷
一.选择题(共6小题,满分18分,每小题3分)
1.下列各式属于最简二次根式的是( )
A. B. C. D.
2.下列二次根式中,与是同类二次根式的是( )
A. B. C. D.
3.若一元二次方程x2+mx+2=0有两个相等的实数根,则m的值是( )
A.2 B.±2 C.±8 D.±2
4.若a是关于x的方程3x2﹣x﹣1=0的一个根,则2021﹣6a2+2a的值是( )
A.2023 B.2022 C.2020 D.2019
5.若正比例函数y=kx的图象经过第一、三象限,且过点A(m,1)和B(2,m),则k的值为( )
A.﹣ B. C.﹣1 D.1
6.关于x的方程ax2+bx+c=0有两个不相等的实根x1、x2,若x2=2x1,则4b﹣9ac的最大值是( )
A.1 B. C. D.2
二.填空题(共12小题,满分24分,每小题2分)
7.化简= .
8.当代数式有意义时,x应满足的条件 .
9.2+的一个有理化因式是 .
10.已知b>0,化简= .
11.若将方程x2﹣4x+1=0化为(x+m)2=n的形式,则m= .
12.已知,.则代数式x2+y2﹣2xy的值为 .
13.构造一个一元二次方程,二次项系数为1,一个根为﹣3,另一个根为2,则该方程的一般式为 .
14.在实数范围内因式分解:x2﹣3= ,3x2﹣5x+2= .
15.已知函数f(x)=,f(2)= .
16.如果正比例函数的图象经过第二、四象限,那么函数值y随x的增大而 .
17.不等式: x<2x+1的解是 .
18.若一元二次方程2x2﹣3x+c=0无实数根,则c的取值范围为 .
三.解答题(共8小题,满分58分)
19.(6分)计算:
(1)3+2;
(2)(+).
20.(6分)计算:
(1)×(﹣)×(﹣);
(2)2 (x≥0,y≥0).
21.(6分)解方程:x2﹣4x+1=0.
22.(6分)解方程(x2﹣1)2﹣3(x2﹣1)=0时,我们将x2﹣1作为一个整体,设x2﹣1=y,则原方程化为y2﹣3y=0.解得y1=0,y2=3.当y=0时,x2﹣1=0,解得x=1或x=﹣1.当y=3时,x2﹣1=3,解得x=2或x=﹣2.所以,原方程的解为x1=1,x2=﹣1,x3=2,x4=﹣2.
模仿材料中解方程的方法,求方程(x2+2x)2﹣2(x2+2x)﹣3=0的解.
23.(8分)先化简,再求值:,其中a=,b=.
24.(8分)已知关于x的一元二次方程x2+2x+2k﹣4=0有两个实数根.
(1)求k的取值范围.
(2)若k为正整数,且该方程的根都是整数,求k的值及方程的根.
25.(8分)列方程(组)解应用题
端午节期间,某水果超市调查某种水果的销售情况,下面是调查员的对话:
小王:该水果的进价是每千克22元;
小李:当销售价为每千克38元时,每天可售出160千克;若每千克降低3元,每天的销售量将增加120千克.
根据他们的对话,解决下面所给问题:超市每天要获得销售利润3640元,又要尽可能让顾客得到实惠,求这种水果的销售价为每千克多少元?
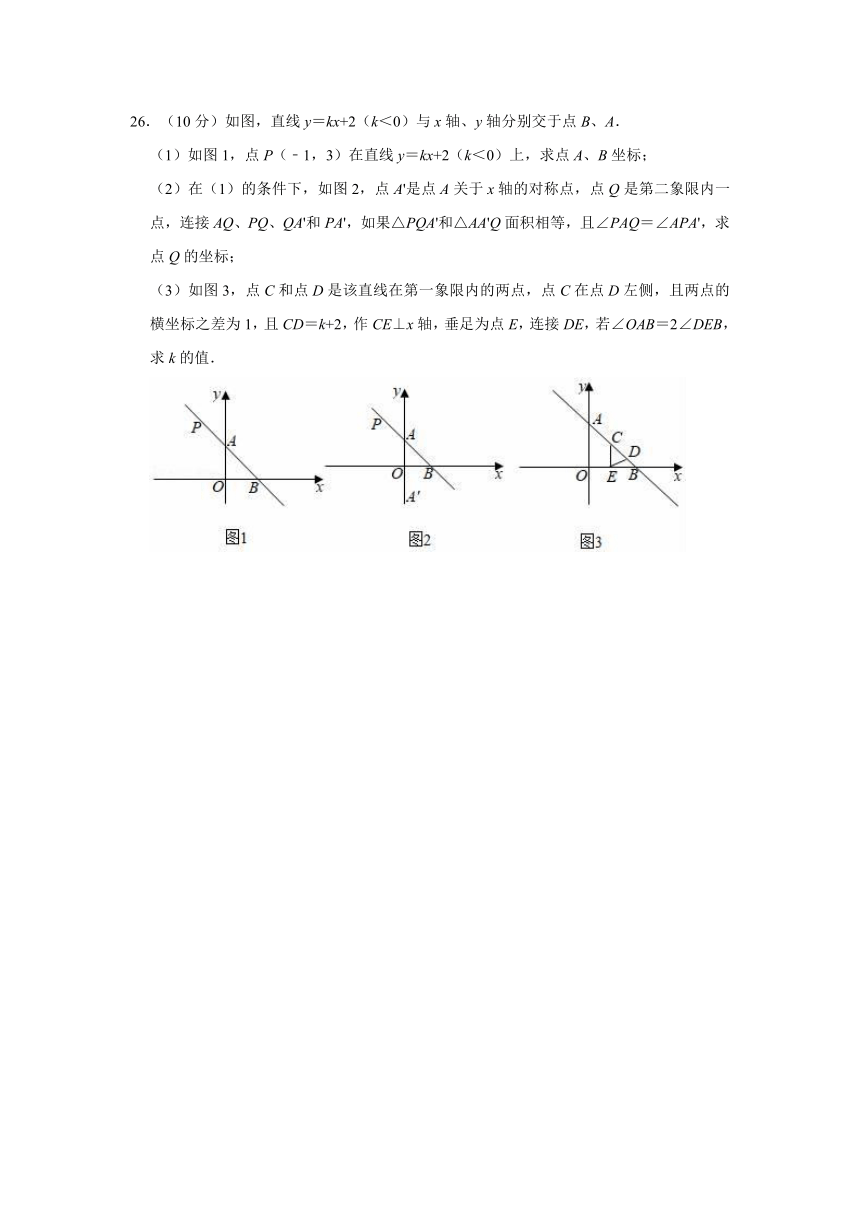
26.(10分)如图,直线y=kx+2(k<0)与x轴、y轴分别交于点B、A.
(1)如图1,点P(﹣1,3)在直线y=kx+2(k<0)上,求点A、B坐标;
(2)在(1)的条件下,如图2,点A'是点A关于x轴的对称点,点Q是第二象限内一点,连接AQ、PQ、QA'和PA',如果△PQA'和△AA'Q面积相等,且∠PAQ=∠APA',求点Q的坐标;
(3)如图3,点C和点D是该直线在第一象限内的两点,点C在点D左侧,且两点的横坐标之差为1,且CD=k+2,作CE⊥x轴,垂足为点E,连接DE,若∠OAB=2∠DEB,求k的值.
参考答案与试题解析
一.选择题(共6小题,满分18分,每小题3分)
1.解:A、含有能开方的因数,不是最简二次根式,故本选项错误;
B、符合最简二次根式的定义,故本选项正确;
C、含有能开方的因式,不是最简二次根式,故本选项错误;
D、被开方数含分母,故本选项错误;
故选:B.
2.解:A、与被开方数不同,不是同类二次根式;
B、=2与被开方数不同,不是同类二次根式;
C、=2与被开方数不同,不是同类二次根式;
D、=2与被开方数相同,是同类二次根式.
故选:D.
3.解:根据题意得Δ=m2﹣4×1×2=0,
解得m=±2.
故选:D.
4.解:∵a是关于x的方程3x2﹣x﹣1=0的一个根,
∴3a2﹣a﹣1=0,
∴3a2﹣a=1,
∴2021﹣6a2+2a=2021﹣2(3a2﹣a)
=2021﹣2×1
=2019.
故选:D.
5.解:∵正比例函数y=kx的图象经过第一、三象限,
∴k>0,
又一次函数图象经过点A(m,1)和B(2,m),
∴,
解得:k=±1,
∵k>0,
∴k=1.
故选:D.
6.解:∵关于x的方程ax2+bx+c=0有两个不相等的实根x1、x2,
∴x1+x2=﹣,
∵x2=2x1,
∴3x1=﹣,即x1=﹣,
∴a+b (﹣)+c=0,
∴﹣+c=0,
∴9ac=2b2,
∴4b﹣9ac=4b﹣2b2=﹣2(b﹣1)2+2,
∵﹣2<0,
∴4b﹣9ac的最大值是2,
故选:D.
二.填空题(共12小题,满分24分,每小题2分)
7.解:∵()2有意义,
∴2x﹣3≥0,
∴x≥1.5,
∴2x﹣1≥3﹣1=2,
∴
=﹣2x+3
=2x﹣1﹣2x+3
=2,
故答案为2.
8.解:∵代数式有意义,
∴4﹣x≥0,x2﹣1≠0,
解得,x≤4且x≠±1,
故答案为:x≤4且x≠±1.
9.解:(2)(2)
=(2)2﹣()2
=4x﹣y,
∴2的一个有理化因式是2,
故答案为:2.
10.解:∵b>0,﹣a3b2>0,
∴a<0,
∴原式=|ab|,
=﹣ab,
故答案为:﹣ab.
11.解:方程x2﹣4x+1=0,
移项得:x2﹣4x=﹣1,
配方得:x2﹣4x+4=3,即(x﹣2)2=3,
则m=﹣2.
故答案为:﹣2.
12.解:∵x=2﹣,y=2+,
∴x﹣y=﹣2,
则x2+y2﹣2xy=(x﹣y)2=(﹣2)2=12,
故答案为:12.
13.解:设该方程为x2﹣mx+n=0,
∴由根与系数的关系可知:﹣3+2=m,﹣3×2=n,
∴m=﹣1,n=﹣6,
∴x2+x﹣6=0,
故答案为:x2+x﹣6=0
14.解:x2﹣3=x2﹣=(x+)(x﹣);
3x2﹣5x+2=(3x﹣2)(x﹣1).
故答案为:(x+)(x﹣);(3x﹣2)(x﹣1).
15.解:f(2)====2+2,
故答案为:2+2.
16.解:正比例函数的图象经过第二、四象限,大致图象如图:
x越大,y越小,
故答案为:减小.
17.解: x<2x+1,
∴x﹣2x<1,
∴()x<1,
∴x>,即:x>,
故答案为:.
18.解:∵一元二次方程2x2﹣3x+c=0无实数根,
Δ=(﹣3)2﹣4×2×c<0,
解得c>,
∴c的取值范围是c>.
故答案为:c>.
三.解答题(共8小题,满分58分)
19.解:(1)原式=5;
(2)原式=×+×
=3+1
=4.
20.解:(1)原式=
=45;
(2)原式=2×
=
=4xy.
21.解:x2﹣4x+1=0
x2﹣4x+4=3
(x﹣2)2=3
x﹣2=
∴x1=2+,x2=2﹣;
22.解:设x2+2x=m,
则m2﹣2m﹣3=0,
∴(m﹣3)(m+1)=0,
∴m﹣3=0或m+1=0,
解得m=3或m=﹣1,
当m=3时,x2+2x=3,即x2+2x﹣3=0,
∴(x+3)(x﹣1)=0,
则x+3=0或x﹣1=0,
解得x1=﹣3,x2=1;
当m=﹣1时,x2+2x=﹣1,即x2+2x+1=0,
∴(x+1)2=0,
解得x3=x4=﹣1;
综上,原方程的解为x1=﹣3,x2=1,x3=x4=﹣1.
23.解:原式=
=
=
=
=,
a====7﹣4,
当a=7﹣4,b=时,
原式=
=
=7+12.
24.解:(1)∵关于x的一元二次方程x2+2x+2k﹣4=0有两个实数根,
∴Δ=b2﹣4ac≥0,即22﹣4×1×(2k﹣4)≥0,
解得:k≤.
(2)∵k≤,且k为正整数,
∴k=1或k=2.
当k=1时,原方程为:x2+2x﹣2=0,
解得:x1=﹣1﹣,x2=﹣1+,
又∵方程的根都是整数,
∴不符合题意,舍去;
当k=2时,原方程为x2+2x=0,
解得:x1=0,x2=﹣2,均为整数,符合题意.
综上,k的值为2,方程的根为x1=0,x2=﹣2.
25.解:设降低x元,超市每天可获得销售利润3640元,由题意得,
(38﹣x﹣22)(160+×120)=3640,
整理得x2﹣12x+27=0,
∴x=3或x=9.
∵要尽可能让顾客得到实惠,
∴x=9,
∴售价为38﹣9=29元/千克.
答:水果的销售价为每千克29元时,超市每天可获得销售利润3640元.
26.解:(1)当x=0时,y=2,
∴A(0,2),
把点P(﹣1,3)代入直线y=kx+2(k<0)得:﹣k+2=3,
解得:k=﹣1,
∴直线AB的解析式为y=﹣x+2,
当y=0时,﹣x+2=0,
解得:x=2,
∴B(2,0);
(2)分两种情况:
①点Q在直线AB的下方时,过点A'作A'Q∥AB,设AQ与A'P交点为M,延长QP交y轴于点N,如图2所示:
∵平行线间的距离处处相等,且QA'为公共底边,
∴△PQA'和△AA'Q面积相等,
∵∠PAQ=∠APA',
∴MA=MP,
∵A'Q∥AB,
∴∠PAQ=∠AQA',∠APA'=∠PA'Q,
∴∠AQA'=∠PA'Q,
∴A'M=QM,
∴AQ=A'P,
∴△PQA'≌△AA'Q(SAS),
∴∠PQA'=∠AA'Q,PQ=AA',
∵点A'是点A关于x轴的对称点,A(0,2),
∴A'(0,﹣2),
∴PQ=AA'=2+2=4,
由(1)可知OA=OB,
∴∠BAO=45°,
∵A'Q∥AP,
∴∠PQA'=∠AA'Q=45°,
∴∠QNO=90°,
∴QN⊥y轴,
∵P(﹣1,3),
∴PN=1,ON=3,
∴QN=PQ+PN=5,
∴Q(﹣5,3);
②当点Q在直线AB的上方时,如图2﹣1所示:
∵∠PAQ=∠APA',
∴AQ∥A'P,
当PQ∥AA'时,四边形A'PQA是平行四边形,
∴△PQA'的面积=△AA'Q面积,
此时Q(﹣1,7),满足条件;
综上所述,点Q的坐标为(﹣5,3)或(﹣1,7);
(3)过D作DF⊥CE于F,如图3所示:
∵∠CEB=90°,
∴∠CED=90°﹣∠DEB,
∵CE∥OA,
∴∠OAB=∠ECD,
∵∠OAB=2∠DEB,
∴∠ECD=2∠DEB,
∴∠CDE=180°﹣∠ECD﹣∠CED=180°﹣2∠DEB﹣(90°﹣∠DEB)=90°﹣∠DEB,
∴∠CDE=∠CED,
∴CE=CD=k+2,
∵点C在直线y=kx+2上,
∴当y=k+2时,有k+2=kx+2,
∴x=1,
∴点C(1,k+2),D(2,2k+2),
∴DF=1,CF=﹣k,CE=k+2,
在Rt△CDF中,由勾股定理得:CF2+DF2=CD2,
∴CF2+DF2=CE2,
即(﹣k)2+12=(k+2)2,
解得:k=﹣.
一.选择题(共6小题,满分18分,每小题3分)
1.下列各式属于最简二次根式的是( )
A. B. C. D.
2.下列二次根式中,与是同类二次根式的是( )
A. B. C. D.
3.若一元二次方程x2+mx+2=0有两个相等的实数根,则m的值是( )
A.2 B.±2 C.±8 D.±2
4.若a是关于x的方程3x2﹣x﹣1=0的一个根,则2021﹣6a2+2a的值是( )
A.2023 B.2022 C.2020 D.2019
5.若正比例函数y=kx的图象经过第一、三象限,且过点A(m,1)和B(2,m),则k的值为( )
A.﹣ B. C.﹣1 D.1
6.关于x的方程ax2+bx+c=0有两个不相等的实根x1、x2,若x2=2x1,则4b﹣9ac的最大值是( )
A.1 B. C. D.2
二.填空题(共12小题,满分24分,每小题2分)
7.化简= .
8.当代数式有意义时,x应满足的条件 .
9.2+的一个有理化因式是 .
10.已知b>0,化简= .
11.若将方程x2﹣4x+1=0化为(x+m)2=n的形式,则m= .
12.已知,.则代数式x2+y2﹣2xy的值为 .
13.构造一个一元二次方程,二次项系数为1,一个根为﹣3,另一个根为2,则该方程的一般式为 .
14.在实数范围内因式分解:x2﹣3= ,3x2﹣5x+2= .
15.已知函数f(x)=,f(2)= .
16.如果正比例函数的图象经过第二、四象限,那么函数值y随x的增大而 .
17.不等式: x<2x+1的解是 .
18.若一元二次方程2x2﹣3x+c=0无实数根,则c的取值范围为 .
三.解答题(共8小题,满分58分)
19.(6分)计算:
(1)3+2;
(2)(+).
20.(6分)计算:
(1)×(﹣)×(﹣);
(2)2 (x≥0,y≥0).
21.(6分)解方程:x2﹣4x+1=0.
22.(6分)解方程(x2﹣1)2﹣3(x2﹣1)=0时,我们将x2﹣1作为一个整体,设x2﹣1=y,则原方程化为y2﹣3y=0.解得y1=0,y2=3.当y=0时,x2﹣1=0,解得x=1或x=﹣1.当y=3时,x2﹣1=3,解得x=2或x=﹣2.所以,原方程的解为x1=1,x2=﹣1,x3=2,x4=﹣2.
模仿材料中解方程的方法,求方程(x2+2x)2﹣2(x2+2x)﹣3=0的解.
23.(8分)先化简,再求值:,其中a=,b=.
24.(8分)已知关于x的一元二次方程x2+2x+2k﹣4=0有两个实数根.
(1)求k的取值范围.
(2)若k为正整数,且该方程的根都是整数,求k的值及方程的根.
25.(8分)列方程(组)解应用题
端午节期间,某水果超市调查某种水果的销售情况,下面是调查员的对话:
小王:该水果的进价是每千克22元;
小李:当销售价为每千克38元时,每天可售出160千克;若每千克降低3元,每天的销售量将增加120千克.
根据他们的对话,解决下面所给问题:超市每天要获得销售利润3640元,又要尽可能让顾客得到实惠,求这种水果的销售价为每千克多少元?
26.(10分)如图,直线y=kx+2(k<0)与x轴、y轴分别交于点B、A.
(1)如图1,点P(﹣1,3)在直线y=kx+2(k<0)上,求点A、B坐标;
(2)在(1)的条件下,如图2,点A'是点A关于x轴的对称点,点Q是第二象限内一点,连接AQ、PQ、QA'和PA',如果△PQA'和△AA'Q面积相等,且∠PAQ=∠APA',求点Q的坐标;
(3)如图3,点C和点D是该直线在第一象限内的两点,点C在点D左侧,且两点的横坐标之差为1,且CD=k+2,作CE⊥x轴,垂足为点E,连接DE,若∠OAB=2∠DEB,求k的值.
参考答案与试题解析
一.选择题(共6小题,满分18分,每小题3分)
1.解:A、含有能开方的因数,不是最简二次根式,故本选项错误;
B、符合最简二次根式的定义,故本选项正确;
C、含有能开方的因式,不是最简二次根式,故本选项错误;
D、被开方数含分母,故本选项错误;
故选:B.
2.解:A、与被开方数不同,不是同类二次根式;
B、=2与被开方数不同,不是同类二次根式;
C、=2与被开方数不同,不是同类二次根式;
D、=2与被开方数相同,是同类二次根式.
故选:D.
3.解:根据题意得Δ=m2﹣4×1×2=0,
解得m=±2.
故选:D.
4.解:∵a是关于x的方程3x2﹣x﹣1=0的一个根,
∴3a2﹣a﹣1=0,
∴3a2﹣a=1,
∴2021﹣6a2+2a=2021﹣2(3a2﹣a)
=2021﹣2×1
=2019.
故选:D.
5.解:∵正比例函数y=kx的图象经过第一、三象限,
∴k>0,
又一次函数图象经过点A(m,1)和B(2,m),
∴,
解得:k=±1,
∵k>0,
∴k=1.
故选:D.
6.解:∵关于x的方程ax2+bx+c=0有两个不相等的实根x1、x2,
∴x1+x2=﹣,
∵x2=2x1,
∴3x1=﹣,即x1=﹣,
∴a+b (﹣)+c=0,
∴﹣+c=0,
∴9ac=2b2,
∴4b﹣9ac=4b﹣2b2=﹣2(b﹣1)2+2,
∵﹣2<0,
∴4b﹣9ac的最大值是2,
故选:D.
二.填空题(共12小题,满分24分,每小题2分)
7.解:∵()2有意义,
∴2x﹣3≥0,
∴x≥1.5,
∴2x﹣1≥3﹣1=2,
∴
=﹣2x+3
=2x﹣1﹣2x+3
=2,
故答案为2.
8.解:∵代数式有意义,
∴4﹣x≥0,x2﹣1≠0,
解得,x≤4且x≠±1,
故答案为:x≤4且x≠±1.
9.解:(2)(2)
=(2)2﹣()2
=4x﹣y,
∴2的一个有理化因式是2,
故答案为:2.
10.解:∵b>0,﹣a3b2>0,
∴a<0,
∴原式=|ab|,
=﹣ab,
故答案为:﹣ab.
11.解:方程x2﹣4x+1=0,
移项得:x2﹣4x=﹣1,
配方得:x2﹣4x+4=3,即(x﹣2)2=3,
则m=﹣2.
故答案为:﹣2.
12.解:∵x=2﹣,y=2+,
∴x﹣y=﹣2,
则x2+y2﹣2xy=(x﹣y)2=(﹣2)2=12,
故答案为:12.
13.解:设该方程为x2﹣mx+n=0,
∴由根与系数的关系可知:﹣3+2=m,﹣3×2=n,
∴m=﹣1,n=﹣6,
∴x2+x﹣6=0,
故答案为:x2+x﹣6=0
14.解:x2﹣3=x2﹣=(x+)(x﹣);
3x2﹣5x+2=(3x﹣2)(x﹣1).
故答案为:(x+)(x﹣);(3x﹣2)(x﹣1).
15.解:f(2)====2+2,
故答案为:2+2.
16.解:正比例函数的图象经过第二、四象限,大致图象如图:
x越大,y越小,
故答案为:减小.
17.解: x<2x+1,
∴x﹣2x<1,
∴()x<1,
∴x>,即:x>,
故答案为:.
18.解:∵一元二次方程2x2﹣3x+c=0无实数根,
Δ=(﹣3)2﹣4×2×c<0,
解得c>,
∴c的取值范围是c>.
故答案为:c>.
三.解答题(共8小题,满分58分)
19.解:(1)原式=5;
(2)原式=×+×
=3+1
=4.
20.解:(1)原式=
=45;
(2)原式=2×
=
=4xy.
21.解:x2﹣4x+1=0
x2﹣4x+4=3
(x﹣2)2=3
x﹣2=
∴x1=2+,x2=2﹣;
22.解:设x2+2x=m,
则m2﹣2m﹣3=0,
∴(m﹣3)(m+1)=0,
∴m﹣3=0或m+1=0,
解得m=3或m=﹣1,
当m=3时,x2+2x=3,即x2+2x﹣3=0,
∴(x+3)(x﹣1)=0,
则x+3=0或x﹣1=0,
解得x1=﹣3,x2=1;
当m=﹣1时,x2+2x=﹣1,即x2+2x+1=0,
∴(x+1)2=0,
解得x3=x4=﹣1;
综上,原方程的解为x1=﹣3,x2=1,x3=x4=﹣1.
23.解:原式=
=
=
=
=,
a====7﹣4,
当a=7﹣4,b=时,
原式=
=
=7+12.
24.解:(1)∵关于x的一元二次方程x2+2x+2k﹣4=0有两个实数根,
∴Δ=b2﹣4ac≥0,即22﹣4×1×(2k﹣4)≥0,
解得:k≤.
(2)∵k≤,且k为正整数,
∴k=1或k=2.
当k=1时,原方程为:x2+2x﹣2=0,
解得:x1=﹣1﹣,x2=﹣1+,
又∵方程的根都是整数,
∴不符合题意,舍去;
当k=2时,原方程为x2+2x=0,
解得:x1=0,x2=﹣2,均为整数,符合题意.
综上,k的值为2,方程的根为x1=0,x2=﹣2.
25.解:设降低x元,超市每天可获得销售利润3640元,由题意得,
(38﹣x﹣22)(160+×120)=3640,
整理得x2﹣12x+27=0,
∴x=3或x=9.
∵要尽可能让顾客得到实惠,
∴x=9,
∴售价为38﹣9=29元/千克.
答:水果的销售价为每千克29元时,超市每天可获得销售利润3640元.
26.解:(1)当x=0时,y=2,
∴A(0,2),
把点P(﹣1,3)代入直线y=kx+2(k<0)得:﹣k+2=3,
解得:k=﹣1,
∴直线AB的解析式为y=﹣x+2,
当y=0时,﹣x+2=0,
解得:x=2,
∴B(2,0);
(2)分两种情况:
①点Q在直线AB的下方时,过点A'作A'Q∥AB,设AQ与A'P交点为M,延长QP交y轴于点N,如图2所示:
∵平行线间的距离处处相等,且QA'为公共底边,
∴△PQA'和△AA'Q面积相等,
∵∠PAQ=∠APA',
∴MA=MP,
∵A'Q∥AB,
∴∠PAQ=∠AQA',∠APA'=∠PA'Q,
∴∠AQA'=∠PA'Q,
∴A'M=QM,
∴AQ=A'P,
∴△PQA'≌△AA'Q(SAS),
∴∠PQA'=∠AA'Q,PQ=AA',
∵点A'是点A关于x轴的对称点,A(0,2),
∴A'(0,﹣2),
∴PQ=AA'=2+2=4,
由(1)可知OA=OB,
∴∠BAO=45°,
∵A'Q∥AP,
∴∠PQA'=∠AA'Q=45°,
∴∠QNO=90°,
∴QN⊥y轴,
∵P(﹣1,3),
∴PN=1,ON=3,
∴QN=PQ+PN=5,
∴Q(﹣5,3);
②当点Q在直线AB的上方时,如图2﹣1所示:
∵∠PAQ=∠APA',
∴AQ∥A'P,
当PQ∥AA'时,四边形A'PQA是平行四边形,
∴△PQA'的面积=△AA'Q面积,
此时Q(﹣1,7),满足条件;
综上所述,点Q的坐标为(﹣5,3)或(﹣1,7);
(3)过D作DF⊥CE于F,如图3所示:
∵∠CEB=90°,
∴∠CED=90°﹣∠DEB,
∵CE∥OA,
∴∠OAB=∠ECD,
∵∠OAB=2∠DEB,
∴∠ECD=2∠DEB,
∴∠CDE=180°﹣∠ECD﹣∠CED=180°﹣2∠DEB﹣(90°﹣∠DEB)=90°﹣∠DEB,
∴∠CDE=∠CED,
∴CE=CD=k+2,
∵点C在直线y=kx+2上,
∴当y=k+2时,有k+2=kx+2,
∴x=1,
∴点C(1,k+2),D(2,2k+2),
∴DF=1,CF=﹣k,CE=k+2,
在Rt△CDF中,由勾股定理得:CF2+DF2=CD2,
∴CF2+DF2=CE2,
即(﹣k)2+12=(k+2)2,
解得:k=﹣.
同课章节目录
