2021-2022学年沪教新版七年级上册数学期中复习试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年沪教新版七年级上册数学期中复习试卷(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 127.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-08 07:38:30 | ||
图片预览




文档简介
2021-2022学年沪教新版七年级上册数学期中复习试卷
一.选择题(共6小题,满分18分,每小题3分)
1.下列各选项中的两个单项式,是同类项的是( )
A.3和2 B.﹣a2和﹣52
C.﹣ a2b和ab2 D.2ab和2xy
2.下列计算正确的是( )
A.b3 b3=2b3 B.(ab2)3=ab6 C.(a5)2=a10 D.y3+y3=y6
3.下列说法中,正确的是( )
A.1不是单项式
B.﹣的系数是﹣5
C.﹣x2y是3次单项式
D.2x2+3xy﹣1是四次三项式
4.若二次三项式ax2+bx+c=(a1x+c1)(a2x+c2),则当a>0,b<0,c>0时,c1,c2的符号为( )
A.c1>0,c2>0 B.c1<0,c2<0 C.c1>0,c2<0 D.c1,c2同号
5.把六张形状大小完全相同的小长方形卡片(如图1)不重叠地放在一个底面为长方形(长为20cm,宽为16cm)的盒子底部(如图2),盒子底面未被卡片覆盖的部分用阴影表示,则图2中两块阴影部分的周长和是( )
A.64cm B.68cm C.72cm D.76cm
6.如图(1),是一个长为2a宽为2b(a>b)的矩形,用剪刀沿矩形的两条对角轴剪开,把它分成四个全等的小矩形,然后按图(2)拼成一个新的正方形,则中间空白部分的面积是( )
A.ab B.(a+b)2 C.(a﹣b)2 D.a2﹣b2
二.填空题(共12小题,满分24分,每小题2分)
7.张老师用长8a的铁丝做了一个长方形教具,其中一边长为b﹣a,则另一边的长为 .
8.将多项式2﹣3xy2+5x3y﹣x2y3按字母y降幂排列是 .
9.计算﹣3a (2b)= .
10.若a2﹣2a﹣1=0,则代数式2a2﹣4a+3的值为 .
11.两船从同一港口同时出发反向而行,甲船顺水,乙船逆水,两船在静水中的速度都是50km/h,水流速度是akm/h,3h后甲船比乙船多航行 km.
12.已知(x+a)(x2﹣x)的展开式中不含x2项,则a= .
13.如果a的相反数是2,那么(a+1)101的值为 .
14.若x﹣y=6,xy=7,则x2+y2的值等于 .
15.已知a2+2a=5,则2a2+4a﹣5的值为 .
16.三个连续奇数中,最小的一个是2n﹣1,则这三个连续奇数的和是 .
17.若2n+2n+2n+2n=28,则n= .
18.甲数x的与乙数y的的差可以表示为 ,若|x|+3=|x﹣3|,则x的取值范围是 .
三.解答题(共9小题,满分58分)
19.(6分)计算:
(1)(2x)3 (﹣5xy2);
(2)a3 a4 a+(a2)4+(﹣2a4)2.
20.(6分)利用乘法公式计算:
(1)198×202;
(2)(2y+1)(﹣2y﹣1).
21.(6分)把下列各式进行因式分解:
(1)a(m+n)﹣b(m+n);
(2)(a+b)(a﹣b)﹣(b+a);
(3)m(a﹣3)﹣n(3﹣a);
(4)x(x﹣y)+y(y﹣x).
22.(6分)分解因式:a2+b2﹣c2﹣4d2﹣2ab+4cd.
23.(6分)速算:
(1)3.14×7.5+3.14×2.5;
(2)4.298×3.256﹣3.256×3.298;
(3)10042﹣9962;
(4)652+2×35×65+352.
24.(6分)阅读下列材料,然后解答问题:
问题:分解因式:x3+4x2﹣5.
解答:把x=1代入多项式x3+4x2﹣5,发现此多项式的值为0,由此确定多项式x3+4x2﹣5中有因式(x﹣1),于是可设x3+4x2﹣5=(x﹣1)(x2+mx+n),分别求出m,n的值.再代入x3+4x2﹣5=(x﹣1)(x2+mx+n),就容易分解多项式x3+4x2﹣5,这种分解因式的方法叫做“试根法”.
(1)求上述式子中m,n的值;
(2)请你用“试根法”分解因式:x3+x2﹣9x﹣9.
25.(6分)2019年双“十一”期间,天猫商场某书店制定了促销方案:若一次性购书超过300元,其中300元按九五折优惠,超过300元的部分按八折优惠.
(1)设一次性购买的书箱原价是a元,当a超过300时,实际付款为 元;(用含a的代数式表示,并化简)
(2)若小明购书时一次性付款365元,则所购书籍的原价是多少元?
(3)小冬在促销期间先后两次下单购买书箱,两次所购书籍的原价之和为600元(第一次所购书籍的原价高于第二次),两次实际共付款555元,则小冬两次购物所购书籍的原价分别是多少元?
26.(8分)因为x2+2x﹣3=(x+3)(x﹣1),这说明多项式x2+2x﹣3有一个因式为x﹣1,我们把x=1代入此多项式发现x=1能使多项式x2+2x﹣3的值为0.
利用上述阅读材料求解:
(1)若x﹣3是多项式x2+kx+12的一个因式,求k的值;
(2)若(x﹣3)和(x﹣4)是多项式x3+mx2+12x+n的两个因式,试求m,n的值.
(3)在(2)的条件下,把多项式x3+mx2+12x+n因式分解.
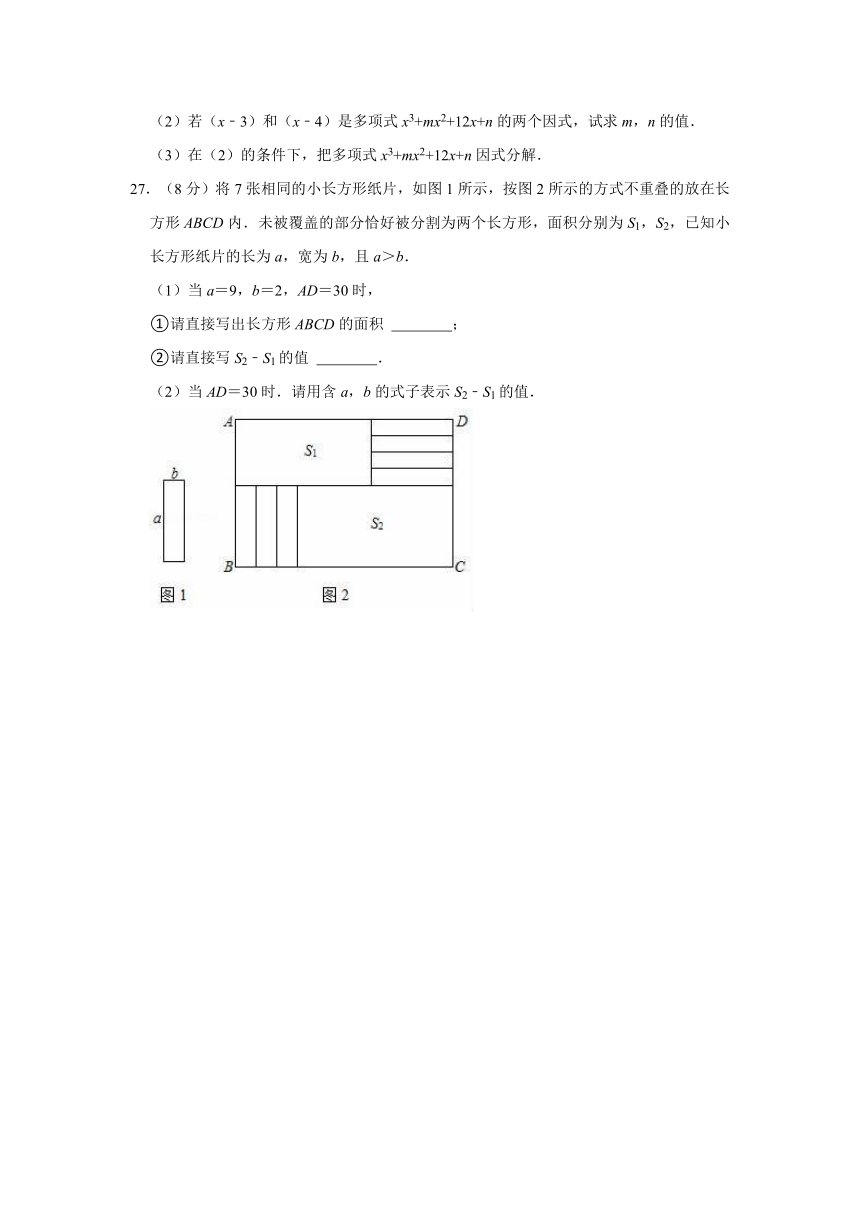
27.(8分)将7张相同的小长方形纸片,如图1所示,按图2所示的方式不重叠的放在长方形ABCD内.未被覆盖的部分恰好被分割为两个长方形,面积分别为S1,S2,已知小长方形纸片的长为a,宽为b,且a>b.
(1)当a=9,b=2,AD=30时,
①请直接写出长方形ABCD的面积 ;
②请直接写S2﹣S1的值 .
(2)当AD=30时.请用含a,b的式子表示S2﹣S1的值.
参考答案与试题解析
一.选择题(共6小题,满分18分,每小题3分)
1.解:A、3和2是同类项;
B、﹣52不含字母,与﹣a2不是同类项;
C、a与b的指数不同,不是同类项;
D、所含字母不同,不是同类项.
故选:A.
2.解:A、b3 b3=b6,故此选项不符合题意;
B、(ab2)3=a3b6,故此选项不符合题意;
C、(a5)2=a10,故此选项符合题意;
D、y3+y3=2y3,故此选项不符合题意;
故选:C.
3.解:A、1是单项式,原说法错误,故此选项不符合题意;
B、单项式﹣的系数是﹣,原说法错误,故此选项不符合题意;
C、﹣x2y是3次单项式,原说法正确,故此选项符合题意;
D、2x2+3xy﹣1是二次三项式,原说法错误,故此选项不符合题意;
故选:C.
4.解:∵ax2+bx+c=(a1x+c1)(a2x+c2),
∴ax2+bx+c=a1a2x2+a1c2x+a2c1x+c1c2,
ax2+bx+c=a1a2x2+(a1c2+a2c1)x+c1c2,
∴a=a1a2,b=a1c2+a2c1,c=c1c2,
∵a>0,b<0,c>0,
∴a1a2>0,a1c2+a2c1<0,c1c2>0,
∴a1,a2同号,c1,c2同号,
∴C不符合题意;
∵a>0,分解因式后一次项系数为正数,即a1>0,a2>0,
∴c1<0,c2<0,
故选:B.
5.解:设小长方形长为xcm,宽为ycm,
由题意得:x+3y=20,
阴影部分周长的和是:20×2+(16﹣3y+16﹣x)×2=104﹣6y﹣2x=104﹣2(3y+x)=104﹣40=64(cm),
故选:A.
6.解:由题意可得,正方形的边长为(a+b),
故正方形的面积为(a+b)2,
又∵原矩形的面积为4ab,
∴中间空的部分的面积=(a+b)2﹣4ab=(a﹣b)2.
故选:C.
二.填空题(共12小题,满分24分,每小题2分)
7.解:另外一边的长度为=4a﹣(b﹣a)=5a﹣b,
故答案为:5a﹣b.
8.解:将多项式2﹣3xy2+5x3y﹣x2y3按字母y的降幂排列是﹣x2y3﹣3xy2+5x3y+2.
故答案为:﹣ x2y3﹣3xy2+5x3y+2.
9.解:﹣3a (2b)=﹣6ab;
故答案为:﹣6ab.
10.解:∵a2﹣2a﹣1=0,
∴a2﹣2a=1,
∴2a2﹣4a+3
=2(a2﹣2a)+3
=2×1+3
=2+3
=5.
故答案为:5.
11.解:3h后甲船航行的路程为3×(50+a)=150+3a(km),
3h后乙船航行的路程为3(50﹣a)=150﹣3a(km),
则3h后甲船比乙船多航行150+3a﹣(150﹣3a)=6a(km),
故答案为:6a.
12.解:(x+a)(x2﹣x)
=x3+ax2﹣x2﹣ax
=x3+(a﹣1)x2﹣ax.
∵展开式中不含x2项,
∴a﹣1=0.
即a=1.
13.解:∵a的相反数是2,
∴a=﹣2,
∴(a+1)101=﹣1.
故答案为:﹣1.
14.解:因为x﹣y=6,xy=7,
所以x2+y2=(x﹣y)2+2xy=62+2×7=50,
故答案为:50.
15.解:∵a2+2a=5,
∴2a2+4a﹣5=2(a2+2a)﹣5=2×5﹣5=5.
故答案为:5.
16.解:∵三个连续奇数中,最小的一个是2n﹣1,
∴这三个连续的奇数为:2n﹣1,2n+1,2n+3,
∴其和=(2n﹣1)+(2n+1)+(2n+3)=2n﹣1+2n+1+2n+3=6n+3.
故答案为:6n+3.
17.解:∵2n+2n+2n+2n=4×2n=22×2n=28,
∴2+n=8,
解得n=6.
故答案为:6.
18.解:甲数x的与乙数y的的差可以表示为: x﹣y.
若|x|+3=|x﹣3|,
①当x≥3时,原式可化为:x+3=x﹣3,无解;
②当0≤x<3时,原式可化为:x+3=3﹣x,此时x=0;
③当x<0时,原式可化为:﹣x+3=3﹣x,等式恒成立.
综上所述,则x≤0.
故答案是: x﹣y;x≤0.
三.解答题(共9小题,满分58分)
19.解:(1)原式=8x3 (﹣5xy2)=﹣40x4y2;
(2)原式=a8+a8+4a8=6a8.
20.解:(1)原式=(200﹣2)(200+2)
=2002﹣22
=40000﹣4
=39996;
(2)原式=﹣(2y+1)2
=﹣(4y2+2×2y×1+12)
=﹣(4y2+4y+1)
=﹣4y2﹣4y﹣1.
21.解:(1)a(m+n)﹣b(m+n)=(m+n)(a﹣b);
(2)(a+b)(a﹣b)﹣(b+a)=(a+b)(a﹣b﹣1);
(3)m(a﹣3)﹣n(3﹣a)=m(a﹣3)+n(a﹣3)=(a﹣3)(m+n);
(4)x(x﹣y)+y(y﹣x)=x(x﹣y)﹣y(x﹣y)=(x﹣y)(x﹣y)=(x﹣y)2.
22.解:a2+b2﹣c2﹣4d2﹣2ab+4cd
=a2﹣2ab+b2﹣(c2﹣4cd+4d2)
=(a﹣b)2﹣(c﹣2d)2
=[(a﹣b)+(c﹣2d)][(a﹣b)﹣(c﹣2d)]
=(a﹣b+c﹣2d)(a﹣b﹣c+2d).
23.解:(1)3.14×7.5+3.14×2.5
=3.14×(7.5+2.5)
=3.14×10
=31.4;
(2)4.298×3.256﹣3.256×3.298
=3.256×(4.298﹣3.298)
=3.256×1
=3.256;
(3)10042﹣9962
=(1004+996)(1004﹣996)
=2000×8
=16000;
(4)652+2×35×65+352
=(65+35)2
=1002
=10000.
24.解:(1)把x=1代入多项式x3+4x2﹣5,多项式的值为0,
∴多项式x3+4x2﹣5中有因式(x﹣1),
于是可设x3+4x2﹣5=(x﹣1)(x2+mx+n)=x3+(m﹣1)x2+(n﹣m)x﹣n,
∴m﹣1=4,n﹣m=0,
∴m=5,n=5,
(2)把x=﹣1代入x3+x2﹣9x﹣9,多项式的值为0,
∴多项式x3+x2﹣9x﹣9中有因式(x+1),
于是可设x3+x2﹣9x﹣9=(x+1)(x2+mx+n)=x3+(m+1)x2+(n+m)x﹣n,
∴m+1=1,n+m=﹣9,
∴m=0,n=﹣9,
∴x3+x2﹣9x﹣9=(x+1)(x2﹣9)=(x+1)(x+3)(x﹣3).
25.解:(1)由题意知,300×0.95+0.8(a﹣300)=0.8a+45
故答案是:(0.8a+45);
(2)设所购书籍的原价是x元,
由题意知,x>300.
故0.8x+45=365.
解得x=400
答:若小明购书时一次性付款365元,则所购书籍的原价是400元;
(3)∵第一次所购书籍的原价高于第二次,
∴第一次所购书籍的原价超过300元,第二次所购书籍的原价低于300元.
设第一次所购书籍的原价是b元,则第二次所购书籍的原价是(600﹣b)元,
由题意知,0.8b+45+(600﹣b)=555
解得b=450,
则600﹣b=150.
答:第一次所购书籍的原价是450元,则第二次所购书籍的原价是150元.
26.解:(1)∵x﹣3是多项式x2+kx+12的一个因式
∴x=3时,x2+kx+12=0
∴9+3k+12=0
∴3k=﹣21
∴k=﹣7
∴k的值为﹣7.
(2)(x﹣3)和(x﹣4)是多项式x3+mx2+12x+n的两个因式
∴x=3和x=4时,x3+mx2+12x+n=0
∴
解得
∴m、n的值分别为﹣7和0.
(3)∵m=﹣7,n=0,
∴x3+mx2+12x+n可化为:x3﹣7x2+12x
∴x3﹣7x2+12x
=x(x2﹣7x+12)
=x(x﹣3)(x﹣4)
27.解:(1)①由题意可得:CD=a+4b,
∴S长方形ABCD=AD CD=AD(a+4b),
当a=9,b=2,AD=30时,
S长方形ABCD=30×(9+4×2)=30×17=510,
故答案为:510;
②由题意可得:S2=a(AD﹣3b),S1=4b(AD﹣a),
当a=9,b=2,AD=30时,
S2﹣S1=a(AD﹣3b)﹣4b(AD﹣a)
=9×(30﹣3×2)﹣4×2×(30﹣9)
=9×24﹣8×21
=216﹣168
=48,
故答案为:48;
(2)∵S2=a(AD﹣3b),S1=4b(AD﹣a),
∴当AD=30时,
S2﹣S1=a(AD﹣3b)﹣4b(AD﹣a)
=a(30﹣3b)﹣4b(30﹣a)
=30a﹣3ab﹣120b+4ab
=30a+ab﹣120b.
一.选择题(共6小题,满分18分,每小题3分)
1.下列各选项中的两个单项式,是同类项的是( )
A.3和2 B.﹣a2和﹣52
C.﹣ a2b和ab2 D.2ab和2xy
2.下列计算正确的是( )
A.b3 b3=2b3 B.(ab2)3=ab6 C.(a5)2=a10 D.y3+y3=y6
3.下列说法中,正确的是( )
A.1不是单项式
B.﹣的系数是﹣5
C.﹣x2y是3次单项式
D.2x2+3xy﹣1是四次三项式
4.若二次三项式ax2+bx+c=(a1x+c1)(a2x+c2),则当a>0,b<0,c>0时,c1,c2的符号为( )
A.c1>0,c2>0 B.c1<0,c2<0 C.c1>0,c2<0 D.c1,c2同号
5.把六张形状大小完全相同的小长方形卡片(如图1)不重叠地放在一个底面为长方形(长为20cm,宽为16cm)的盒子底部(如图2),盒子底面未被卡片覆盖的部分用阴影表示,则图2中两块阴影部分的周长和是( )
A.64cm B.68cm C.72cm D.76cm
6.如图(1),是一个长为2a宽为2b(a>b)的矩形,用剪刀沿矩形的两条对角轴剪开,把它分成四个全等的小矩形,然后按图(2)拼成一个新的正方形,则中间空白部分的面积是( )
A.ab B.(a+b)2 C.(a﹣b)2 D.a2﹣b2
二.填空题(共12小题,满分24分,每小题2分)
7.张老师用长8a的铁丝做了一个长方形教具,其中一边长为b﹣a,则另一边的长为 .
8.将多项式2﹣3xy2+5x3y﹣x2y3按字母y降幂排列是 .
9.计算﹣3a (2b)= .
10.若a2﹣2a﹣1=0,则代数式2a2﹣4a+3的值为 .
11.两船从同一港口同时出发反向而行,甲船顺水,乙船逆水,两船在静水中的速度都是50km/h,水流速度是akm/h,3h后甲船比乙船多航行 km.
12.已知(x+a)(x2﹣x)的展开式中不含x2项,则a= .
13.如果a的相反数是2,那么(a+1)101的值为 .
14.若x﹣y=6,xy=7,则x2+y2的值等于 .
15.已知a2+2a=5,则2a2+4a﹣5的值为 .
16.三个连续奇数中,最小的一个是2n﹣1,则这三个连续奇数的和是 .
17.若2n+2n+2n+2n=28,则n= .
18.甲数x的与乙数y的的差可以表示为 ,若|x|+3=|x﹣3|,则x的取值范围是 .
三.解答题(共9小题,满分58分)
19.(6分)计算:
(1)(2x)3 (﹣5xy2);
(2)a3 a4 a+(a2)4+(﹣2a4)2.
20.(6分)利用乘法公式计算:
(1)198×202;
(2)(2y+1)(﹣2y﹣1).
21.(6分)把下列各式进行因式分解:
(1)a(m+n)﹣b(m+n);
(2)(a+b)(a﹣b)﹣(b+a);
(3)m(a﹣3)﹣n(3﹣a);
(4)x(x﹣y)+y(y﹣x).
22.(6分)分解因式:a2+b2﹣c2﹣4d2﹣2ab+4cd.
23.(6分)速算:
(1)3.14×7.5+3.14×2.5;
(2)4.298×3.256﹣3.256×3.298;
(3)10042﹣9962;
(4)652+2×35×65+352.
24.(6分)阅读下列材料,然后解答问题:
问题:分解因式:x3+4x2﹣5.
解答:把x=1代入多项式x3+4x2﹣5,发现此多项式的值为0,由此确定多项式x3+4x2﹣5中有因式(x﹣1),于是可设x3+4x2﹣5=(x﹣1)(x2+mx+n),分别求出m,n的值.再代入x3+4x2﹣5=(x﹣1)(x2+mx+n),就容易分解多项式x3+4x2﹣5,这种分解因式的方法叫做“试根法”.
(1)求上述式子中m,n的值;
(2)请你用“试根法”分解因式:x3+x2﹣9x﹣9.
25.(6分)2019年双“十一”期间,天猫商场某书店制定了促销方案:若一次性购书超过300元,其中300元按九五折优惠,超过300元的部分按八折优惠.
(1)设一次性购买的书箱原价是a元,当a超过300时,实际付款为 元;(用含a的代数式表示,并化简)
(2)若小明购书时一次性付款365元,则所购书籍的原价是多少元?
(3)小冬在促销期间先后两次下单购买书箱,两次所购书籍的原价之和为600元(第一次所购书籍的原价高于第二次),两次实际共付款555元,则小冬两次购物所购书籍的原价分别是多少元?
26.(8分)因为x2+2x﹣3=(x+3)(x﹣1),这说明多项式x2+2x﹣3有一个因式为x﹣1,我们把x=1代入此多项式发现x=1能使多项式x2+2x﹣3的值为0.
利用上述阅读材料求解:
(1)若x﹣3是多项式x2+kx+12的一个因式,求k的值;
(2)若(x﹣3)和(x﹣4)是多项式x3+mx2+12x+n的两个因式,试求m,n的值.
(3)在(2)的条件下,把多项式x3+mx2+12x+n因式分解.
27.(8分)将7张相同的小长方形纸片,如图1所示,按图2所示的方式不重叠的放在长方形ABCD内.未被覆盖的部分恰好被分割为两个长方形,面积分别为S1,S2,已知小长方形纸片的长为a,宽为b,且a>b.
(1)当a=9,b=2,AD=30时,
①请直接写出长方形ABCD的面积 ;
②请直接写S2﹣S1的值 .
(2)当AD=30时.请用含a,b的式子表示S2﹣S1的值.
参考答案与试题解析
一.选择题(共6小题,满分18分,每小题3分)
1.解:A、3和2是同类项;
B、﹣52不含字母,与﹣a2不是同类项;
C、a与b的指数不同,不是同类项;
D、所含字母不同,不是同类项.
故选:A.
2.解:A、b3 b3=b6,故此选项不符合题意;
B、(ab2)3=a3b6,故此选项不符合题意;
C、(a5)2=a10,故此选项符合题意;
D、y3+y3=2y3,故此选项不符合题意;
故选:C.
3.解:A、1是单项式,原说法错误,故此选项不符合题意;
B、单项式﹣的系数是﹣,原说法错误,故此选项不符合题意;
C、﹣x2y是3次单项式,原说法正确,故此选项符合题意;
D、2x2+3xy﹣1是二次三项式,原说法错误,故此选项不符合题意;
故选:C.
4.解:∵ax2+bx+c=(a1x+c1)(a2x+c2),
∴ax2+bx+c=a1a2x2+a1c2x+a2c1x+c1c2,
ax2+bx+c=a1a2x2+(a1c2+a2c1)x+c1c2,
∴a=a1a2,b=a1c2+a2c1,c=c1c2,
∵a>0,b<0,c>0,
∴a1a2>0,a1c2+a2c1<0,c1c2>0,
∴a1,a2同号,c1,c2同号,
∴C不符合题意;
∵a>0,分解因式后一次项系数为正数,即a1>0,a2>0,
∴c1<0,c2<0,
故选:B.
5.解:设小长方形长为xcm,宽为ycm,
由题意得:x+3y=20,
阴影部分周长的和是:20×2+(16﹣3y+16﹣x)×2=104﹣6y﹣2x=104﹣2(3y+x)=104﹣40=64(cm),
故选:A.
6.解:由题意可得,正方形的边长为(a+b),
故正方形的面积为(a+b)2,
又∵原矩形的面积为4ab,
∴中间空的部分的面积=(a+b)2﹣4ab=(a﹣b)2.
故选:C.
二.填空题(共12小题,满分24分,每小题2分)
7.解:另外一边的长度为=4a﹣(b﹣a)=5a﹣b,
故答案为:5a﹣b.
8.解:将多项式2﹣3xy2+5x3y﹣x2y3按字母y的降幂排列是﹣x2y3﹣3xy2+5x3y+2.
故答案为:﹣ x2y3﹣3xy2+5x3y+2.
9.解:﹣3a (2b)=﹣6ab;
故答案为:﹣6ab.
10.解:∵a2﹣2a﹣1=0,
∴a2﹣2a=1,
∴2a2﹣4a+3
=2(a2﹣2a)+3
=2×1+3
=2+3
=5.
故答案为:5.
11.解:3h后甲船航行的路程为3×(50+a)=150+3a(km),
3h后乙船航行的路程为3(50﹣a)=150﹣3a(km),
则3h后甲船比乙船多航行150+3a﹣(150﹣3a)=6a(km),
故答案为:6a.
12.解:(x+a)(x2﹣x)
=x3+ax2﹣x2﹣ax
=x3+(a﹣1)x2﹣ax.
∵展开式中不含x2项,
∴a﹣1=0.
即a=1.
13.解:∵a的相反数是2,
∴a=﹣2,
∴(a+1)101=﹣1.
故答案为:﹣1.
14.解:因为x﹣y=6,xy=7,
所以x2+y2=(x﹣y)2+2xy=62+2×7=50,
故答案为:50.
15.解:∵a2+2a=5,
∴2a2+4a﹣5=2(a2+2a)﹣5=2×5﹣5=5.
故答案为:5.
16.解:∵三个连续奇数中,最小的一个是2n﹣1,
∴这三个连续的奇数为:2n﹣1,2n+1,2n+3,
∴其和=(2n﹣1)+(2n+1)+(2n+3)=2n﹣1+2n+1+2n+3=6n+3.
故答案为:6n+3.
17.解:∵2n+2n+2n+2n=4×2n=22×2n=28,
∴2+n=8,
解得n=6.
故答案为:6.
18.解:甲数x的与乙数y的的差可以表示为: x﹣y.
若|x|+3=|x﹣3|,
①当x≥3时,原式可化为:x+3=x﹣3,无解;
②当0≤x<3时,原式可化为:x+3=3﹣x,此时x=0;
③当x<0时,原式可化为:﹣x+3=3﹣x,等式恒成立.
综上所述,则x≤0.
故答案是: x﹣y;x≤0.
三.解答题(共9小题,满分58分)
19.解:(1)原式=8x3 (﹣5xy2)=﹣40x4y2;
(2)原式=a8+a8+4a8=6a8.
20.解:(1)原式=(200﹣2)(200+2)
=2002﹣22
=40000﹣4
=39996;
(2)原式=﹣(2y+1)2
=﹣(4y2+2×2y×1+12)
=﹣(4y2+4y+1)
=﹣4y2﹣4y﹣1.
21.解:(1)a(m+n)﹣b(m+n)=(m+n)(a﹣b);
(2)(a+b)(a﹣b)﹣(b+a)=(a+b)(a﹣b﹣1);
(3)m(a﹣3)﹣n(3﹣a)=m(a﹣3)+n(a﹣3)=(a﹣3)(m+n);
(4)x(x﹣y)+y(y﹣x)=x(x﹣y)﹣y(x﹣y)=(x﹣y)(x﹣y)=(x﹣y)2.
22.解:a2+b2﹣c2﹣4d2﹣2ab+4cd
=a2﹣2ab+b2﹣(c2﹣4cd+4d2)
=(a﹣b)2﹣(c﹣2d)2
=[(a﹣b)+(c﹣2d)][(a﹣b)﹣(c﹣2d)]
=(a﹣b+c﹣2d)(a﹣b﹣c+2d).
23.解:(1)3.14×7.5+3.14×2.5
=3.14×(7.5+2.5)
=3.14×10
=31.4;
(2)4.298×3.256﹣3.256×3.298
=3.256×(4.298﹣3.298)
=3.256×1
=3.256;
(3)10042﹣9962
=(1004+996)(1004﹣996)
=2000×8
=16000;
(4)652+2×35×65+352
=(65+35)2
=1002
=10000.
24.解:(1)把x=1代入多项式x3+4x2﹣5,多项式的值为0,
∴多项式x3+4x2﹣5中有因式(x﹣1),
于是可设x3+4x2﹣5=(x﹣1)(x2+mx+n)=x3+(m﹣1)x2+(n﹣m)x﹣n,
∴m﹣1=4,n﹣m=0,
∴m=5,n=5,
(2)把x=﹣1代入x3+x2﹣9x﹣9,多项式的值为0,
∴多项式x3+x2﹣9x﹣9中有因式(x+1),
于是可设x3+x2﹣9x﹣9=(x+1)(x2+mx+n)=x3+(m+1)x2+(n+m)x﹣n,
∴m+1=1,n+m=﹣9,
∴m=0,n=﹣9,
∴x3+x2﹣9x﹣9=(x+1)(x2﹣9)=(x+1)(x+3)(x﹣3).
25.解:(1)由题意知,300×0.95+0.8(a﹣300)=0.8a+45
故答案是:(0.8a+45);
(2)设所购书籍的原价是x元,
由题意知,x>300.
故0.8x+45=365.
解得x=400
答:若小明购书时一次性付款365元,则所购书籍的原价是400元;
(3)∵第一次所购书籍的原价高于第二次,
∴第一次所购书籍的原价超过300元,第二次所购书籍的原价低于300元.
设第一次所购书籍的原价是b元,则第二次所购书籍的原价是(600﹣b)元,
由题意知,0.8b+45+(600﹣b)=555
解得b=450,
则600﹣b=150.
答:第一次所购书籍的原价是450元,则第二次所购书籍的原价是150元.
26.解:(1)∵x﹣3是多项式x2+kx+12的一个因式
∴x=3时,x2+kx+12=0
∴9+3k+12=0
∴3k=﹣21
∴k=﹣7
∴k的值为﹣7.
(2)(x﹣3)和(x﹣4)是多项式x3+mx2+12x+n的两个因式
∴x=3和x=4时,x3+mx2+12x+n=0
∴
解得
∴m、n的值分别为﹣7和0.
(3)∵m=﹣7,n=0,
∴x3+mx2+12x+n可化为:x3﹣7x2+12x
∴x3﹣7x2+12x
=x(x2﹣7x+12)
=x(x﹣3)(x﹣4)
27.解:(1)①由题意可得:CD=a+4b,
∴S长方形ABCD=AD CD=AD(a+4b),
当a=9,b=2,AD=30时,
S长方形ABCD=30×(9+4×2)=30×17=510,
故答案为:510;
②由题意可得:S2=a(AD﹣3b),S1=4b(AD﹣a),
当a=9,b=2,AD=30时,
S2﹣S1=a(AD﹣3b)﹣4b(AD﹣a)
=9×(30﹣3×2)﹣4×2×(30﹣9)
=9×24﹣8×21
=216﹣168
=48,
故答案为:48;
(2)∵S2=a(AD﹣3b),S1=4b(AD﹣a),
∴当AD=30时,
S2﹣S1=a(AD﹣3b)﹣4b(AD﹣a)
=a(30﹣3b)﹣4b(30﹣a)
=30a﹣3ab﹣120b+4ab
=30a+ab﹣120b.
同课章节目录
