2021-2022学年高一上学期数学北师大版(2019)必修第一册5.1.2 用二分法求方程的近似解 课件(共19张PPT)
文档属性
| 名称 | 2021-2022学年高一上学期数学北师大版(2019)必修第一册5.1.2 用二分法求方程的近似解 课件(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 590.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-09 19:48:41 | ||
图片预览





文档简介
(共19张PPT)
1
1.2用二分法求方程的近似解
复习与引入:
1. 什么是函数的零点?
把函数 的图像与 轴交点的横坐标称为该函数的零点. 即函数 的零点就是方程 的解。
结论:
方程 有实数根
函数 的图像与 轴有交点
函数 有零点
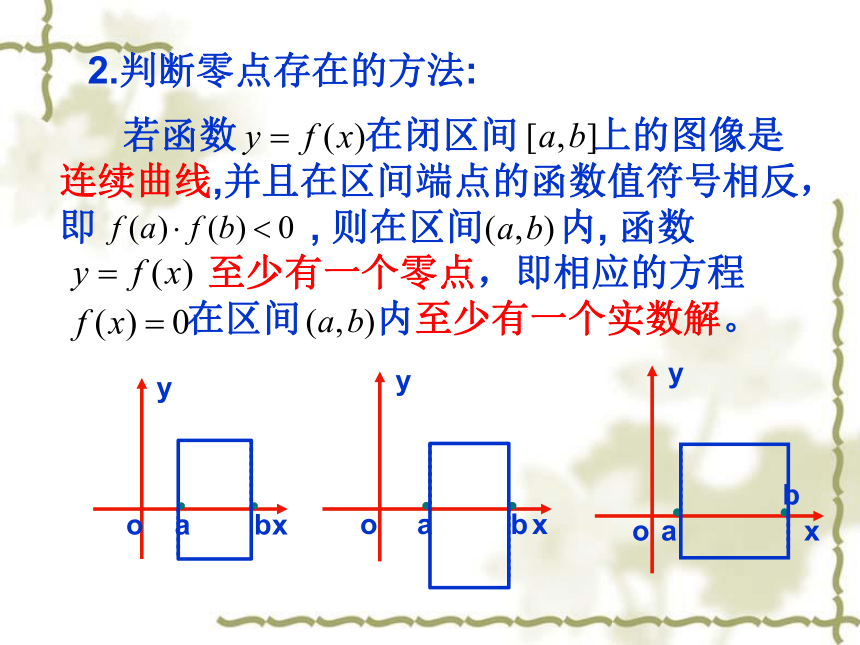
2.判断零点存在的方法:
若函数 在闭区间 上的图像是连续曲线,并且在区间端点的函数值符号相反,即 , 则在区间 内, 函数
至少有一个零点,即相应的方程
在区间 内至少有一个实数解。
x
y
o
a
b
x
y
o
a
b
y
x
o
a
b
函数f(x)=2x3+3x-3在区间[0,1]内有零点
如何找出这个零点?
策略一:用几何画板画出函数的图象,求出其与x轴交点的横坐标
也可以求函数y = 2x3与函数y = 3 – 3x的图象交点的横坐标。
思考:
游戏:请你模仿李咏主持一下幸运52,请同学们猜一下下面这部手机的价格。
利用我们猜价格的方法,你能否求解方程2x3+3x-3=0
如果能求解的话,怎么去解?你能用函数的零点的性质吗?
策略二:“取中点”逐步缩小零点所在的范围
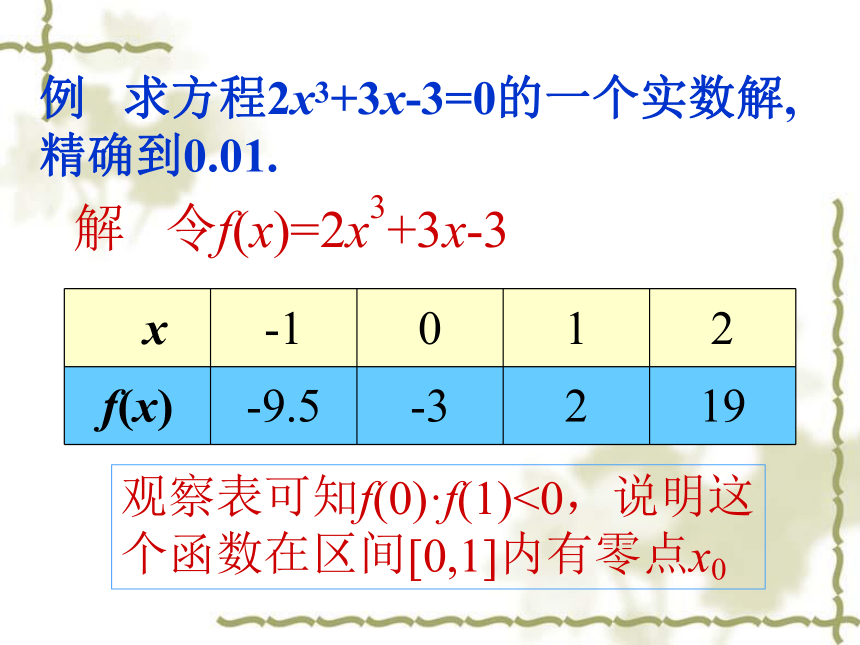
例 求方程2x3+3x-3=0的一个实数解,精确到0.01.
解 令f(x)=2x3+3x-3
x -1 0 1 2
f(x) -9.5 -3 2 19
观察表可知f(0)·f(1)<0,说明这个函数在区间[0,1]内有零点x0
取区间(0,1)的中点 x1=0.5
然后用计算器算得 f(0.5)=-1.25
因为 f(0.5)·f(1)<0
所以 x0∈(0.5,1)
再取区间(0.5,1)的中点x1=0.75
然后用计算器算得 f(0.75)=0.09375
因为 f(0.5)·f(0.75)<0,
所以 x0∈(0.5,0.75).......
左端点 右端点
第1次 0 1
第2次 0.5 1
第3次 0.5 0.75
第4次 0.625 0.75
第5次 0.687 5 0.75
第6次 0.718 75 0.75
第7次 0.734 375 0.75
第8次 0.734 375 0.742 187 5
如此就得到方程实数解所在区间的列表
同理可得
x0∈(0.625,0.75),……
x0∈(0.734375, 0.7421875 )
由于 |0.7421875-0.734375| =0.0078125<0.01
此时区间(0.734375, 0.7421875)的任意一个数都可作为方程的近似解。例如,我们选取0.74作为方程的一个近似解。
1.二分法的定义
对于在区间[a,b]上连续不断且f(a)f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法,叫做二分法.
●想一想:能否用二分法求任何函数(图象是连续的)的近似零点?
提示:不能.看一个函数能否用二分法求其零点的依据是函数图象在零点附近是连续不断的,且在该零点左右函数值异号.
【例1】下列函数图象与x轴均有交点,其中不能用二分法求图中函数零点的是( )
思路分析:由题目可获取以下主要信息:
①题中给出了函数的图象;
②二分法的概念.
解答本题可结合二分法的概念,判断是否具备使用二分法的条件.
1 下列函数中能用二分法求零点的是( )
2.二分法的步骤
给定精确度ε,用二分法求f(x)零点近似值的步骤如下:
(1)确定区间[a,b],验证f(a)·f(b)<0,给定精确度ε;
(2)求区间(a,b)的中点c;
(3)计算f(c);
①若f(c)=0,则c就是函数的零点;
②若f(a)·f(c)<0,则令b=c(此时零点x0∈(a,c));
③若f(c)·f(b)<0,则令a=c(此时零点x0∈(c,b)).
(4)判断是否达到精确度ε:即若|a-b|<ε,则得到零点近似值a(或b);否则重复(2)~(4).
例2 借助计算器或计算机用二分法求方程2x+3x=7的近似解(精确度0.1)
解:原方程即2x+3x=7,令f(x)= 2x+3x-7,用计算机作出函数f(x)= 2x+3x-7的对应值表和图象如下:
x 0 1 2 3 4 5 6 7 8
f(x) -6 -2 3 10 21 40 75 142 273
因为f(1)·f(2)<0所以 f(x)= 2x+3x-7在(1,2)内有零点x0,取(1,2)的中点x1=1.5, f(1.5)= 0.33,因为f(1)·f(1.5)<0所以
x0 ∈(1,1.5)
取(1,1.5)的中点x2=1.25 ,f(1.25)= -0.87,因为f(1.25)·f(1.5)<0,所以x0∈(1.25,1.5)
同理可得, x0∈(1.375,1.5),x0∈ (1.375,1.4375),由于
|1.375-1.4375|=0.0625〈 0.1
所以,原方程的近似解可取为1.4375
抽象概括:
利用二分法求方程实数解的过程
1. 初始区间是一个两端函数值反号的区间;
2. “M”的含义是: 取新区间,一个端点是原区间的中点,另一个端点是原区间两端点中的一个,新区间两端点的函数值反号;
3. “N”的含义是: 方程解满足要求的精度;
4. “P”的含义是:选取区间内的任意一个数作为方程的近似解。
选定初始区间
取区间的中点
中点函数值为零
M
N
P
否
否
是
是
结束
2.设f(x)=3x+2x-8,用二分法求方程3x+2x-8=0在x∈(1,2)内近似解的过程中得f(1)<0,f(1.5)>0,f(1.25)<0,则方程的根在区间( )
A.(1.25,1.5) B.(1,1.25)
C.(1.5,2) D.不能确定
解析:∵f(1.5)>0,f(1.25)<0,∴方程根在区间
(1.25,1.5)内.
答案:A
课堂练习:课本P119练习。
补充练习:
1、方程 ex – x – 2 = 0在实数范围内的解有 个。
2、设函数 ,若f (– 4) = f (0),f (– 2) = – 2,则关于x的方程f (x) = x的解的个数为( )
(A)1 (B)2 (C)3 (D)4
3、讨论方程 的实根的个数。
1.二分法的定义;
2.用二分法求函数零点近似值的步骤。
1
1.2用二分法求方程的近似解
复习与引入:
1. 什么是函数的零点?
把函数 的图像与 轴交点的横坐标称为该函数的零点. 即函数 的零点就是方程 的解。
结论:
方程 有实数根
函数 的图像与 轴有交点
函数 有零点
2.判断零点存在的方法:
若函数 在闭区间 上的图像是连续曲线,并且在区间端点的函数值符号相反,即 , 则在区间 内, 函数
至少有一个零点,即相应的方程
在区间 内至少有一个实数解。
x
y
o
a
b
x
y
o
a
b
y
x
o
a
b
函数f(x)=2x3+3x-3在区间[0,1]内有零点
如何找出这个零点?
策略一:用几何画板画出函数的图象,求出其与x轴交点的横坐标
也可以求函数y = 2x3与函数y = 3 – 3x的图象交点的横坐标。
思考:
游戏:请你模仿李咏主持一下幸运52,请同学们猜一下下面这部手机的价格。
利用我们猜价格的方法,你能否求解方程2x3+3x-3=0
如果能求解的话,怎么去解?你能用函数的零点的性质吗?
策略二:“取中点”逐步缩小零点所在的范围
例 求方程2x3+3x-3=0的一个实数解,精确到0.01.
解 令f(x)=2x3+3x-3
x -1 0 1 2
f(x) -9.5 -3 2 19
观察表可知f(0)·f(1)<0,说明这个函数在区间[0,1]内有零点x0
取区间(0,1)的中点 x1=0.5
然后用计算器算得 f(0.5)=-1.25
因为 f(0.5)·f(1)<0
所以 x0∈(0.5,1)
再取区间(0.5,1)的中点x1=0.75
然后用计算器算得 f(0.75)=0.09375
因为 f(0.5)·f(0.75)<0,
所以 x0∈(0.5,0.75).......
左端点 右端点
第1次 0 1
第2次 0.5 1
第3次 0.5 0.75
第4次 0.625 0.75
第5次 0.687 5 0.75
第6次 0.718 75 0.75
第7次 0.734 375 0.75
第8次 0.734 375 0.742 187 5
如此就得到方程实数解所在区间的列表
同理可得
x0∈(0.625,0.75),……
x0∈(0.734375, 0.7421875 )
由于 |0.7421875-0.734375| =0.0078125<0.01
此时区间(0.734375, 0.7421875)的任意一个数都可作为方程的近似解。例如,我们选取0.74作为方程的一个近似解。
1.二分法的定义
对于在区间[a,b]上连续不断且f(a)f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法,叫做二分法.
●想一想:能否用二分法求任何函数(图象是连续的)的近似零点?
提示:不能.看一个函数能否用二分法求其零点的依据是函数图象在零点附近是连续不断的,且在该零点左右函数值异号.
【例1】下列函数图象与x轴均有交点,其中不能用二分法求图中函数零点的是( )
思路分析:由题目可获取以下主要信息:
①题中给出了函数的图象;
②二分法的概念.
解答本题可结合二分法的概念,判断是否具备使用二分法的条件.
1 下列函数中能用二分法求零点的是( )
2.二分法的步骤
给定精确度ε,用二分法求f(x)零点近似值的步骤如下:
(1)确定区间[a,b],验证f(a)·f(b)<0,给定精确度ε;
(2)求区间(a,b)的中点c;
(3)计算f(c);
①若f(c)=0,则c就是函数的零点;
②若f(a)·f(c)<0,则令b=c(此时零点x0∈(a,c));
③若f(c)·f(b)<0,则令a=c(此时零点x0∈(c,b)).
(4)判断是否达到精确度ε:即若|a-b|<ε,则得到零点近似值a(或b);否则重复(2)~(4).
例2 借助计算器或计算机用二分法求方程2x+3x=7的近似解(精确度0.1)
解:原方程即2x+3x=7,令f(x)= 2x+3x-7,用计算机作出函数f(x)= 2x+3x-7的对应值表和图象如下:
x 0 1 2 3 4 5 6 7 8
f(x) -6 -2 3 10 21 40 75 142 273
因为f(1)·f(2)<0所以 f(x)= 2x+3x-7在(1,2)内有零点x0,取(1,2)的中点x1=1.5, f(1.5)= 0.33,因为f(1)·f(1.5)<0所以
x0 ∈(1,1.5)
取(1,1.5)的中点x2=1.25 ,f(1.25)= -0.87,因为f(1.25)·f(1.5)<0,所以x0∈(1.25,1.5)
同理可得, x0∈(1.375,1.5),x0∈ (1.375,1.4375),由于
|1.375-1.4375|=0.0625〈 0.1
所以,原方程的近似解可取为1.4375
抽象概括:
利用二分法求方程实数解的过程
1. 初始区间是一个两端函数值反号的区间;
2. “M”的含义是: 取新区间,一个端点是原区间的中点,另一个端点是原区间两端点中的一个,新区间两端点的函数值反号;
3. “N”的含义是: 方程解满足要求的精度;
4. “P”的含义是:选取区间内的任意一个数作为方程的近似解。
选定初始区间
取区间的中点
中点函数值为零
M
N
P
否
否
是
是
结束
2.设f(x)=3x+2x-8,用二分法求方程3x+2x-8=0在x∈(1,2)内近似解的过程中得f(1)<0,f(1.5)>0,f(1.25)<0,则方程的根在区间( )
A.(1.25,1.5) B.(1,1.25)
C.(1.5,2) D.不能确定
解析:∵f(1.5)>0,f(1.25)<0,∴方程根在区间
(1.25,1.5)内.
答案:A
课堂练习:课本P119练习。
补充练习:
1、方程 ex – x – 2 = 0在实数范围内的解有 个。
2、设函数 ,若f (– 4) = f (0),f (– 2) = – 2,则关于x的方程f (x) = x的解的个数为( )
(A)1 (B)2 (C)3 (D)4
3、讨论方程 的实根的个数。
1.二分法的定义;
2.用二分法求函数零点近似值的步骤。
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
