27.2.1 第1课时 平行线分线段成比例 课件(共26张PPT)
文档属性
| 名称 | 27.2.1 第1课时 平行线分线段成比例 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-08 23:21:17 | ||
图片预览






文档简介
(共26张PPT)
第二十七章 相似
27.2.1 第1课时 平行线分线段成比例
随堂演练
课堂小结
获取新知
知识回顾
例题讲解
知识回顾
1、什么叫相似多边形呢?
2、什么叫相似比?
对应角相等,对应边成比例的两个多边形叫做相似多边形
相似多边形的对应边的比叫做相似比
获取新知
对应角相等,对应边成比例的两个三角形叫做相似三角形.
则△ ABC ∽△ A′B′C′.
用符号语言表示:
判定三角形全等,我们并不是验证六个条件,而是利用了几个简便的判定定理(SSS,SAS,ASA,AAS),那么判定三角形相似我们又能不能用类似的简便的判定方法呢?
问题 如图,任意画两条直线a,b ,再画三条与a,b 都相交的平行线l1,l2,l3 .探究l1,l2,l3在直线 a,b 上截得的线段有什么关系.
l3
l1
l2
A
B
C
D
E
F
a
b
通过计算可以得到:
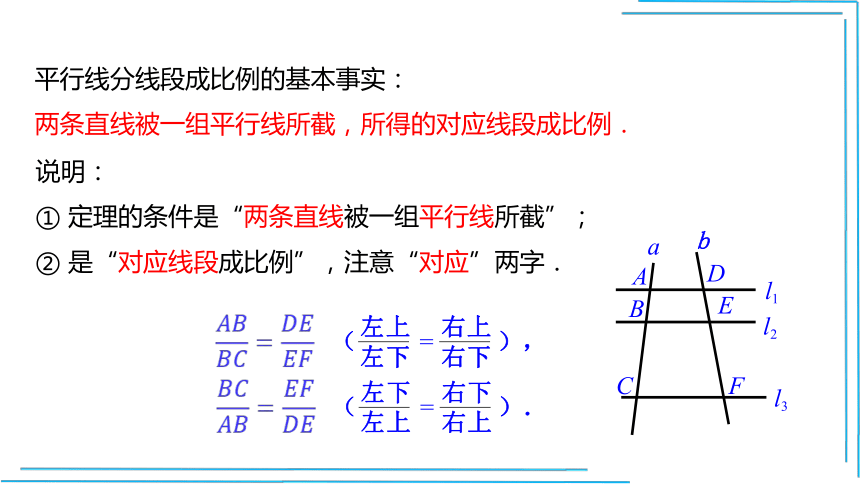
平行线分线段成比例的基本事实:
两条直线被一组平行线所截,所得的对应线段成比例.
说明:
① 定理的条件是“两条直线被一组平行线所截”;
② 是“对应线段成比例”,注意“对应”两字.
l3
l1
l2
A
B
C
D
E
F
a
b
( = ),
左上
左下
右上
右下
( = ).
左下
左上
右下
右上
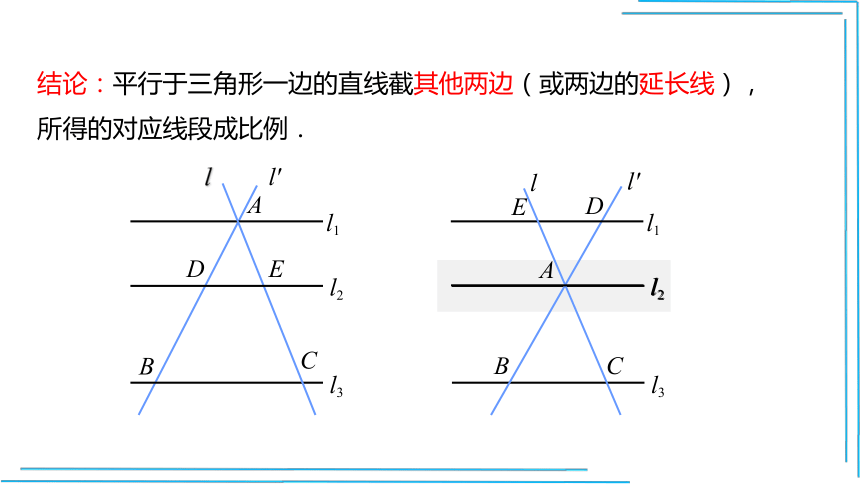
结论:平行于三角形一边的直线截其他两边(或两边的延长线),
所得的对应线段成比例.
l1
l3
l
l'
A
B
C
D
E
l2
l2
l3
A
B
C
D
E
l1
l
l'
l2
思考:如图,在△ABC 中,DE∥BC,且 DE 分别交 AB,AC 于点 D,E,△ADE 与△ABC 有什么关系?
C
A
B
D
E
我们通过度量三角形的边长,知道△ADE∽△ABC,但要用相似的定义去证明它,我们需要证明什么?
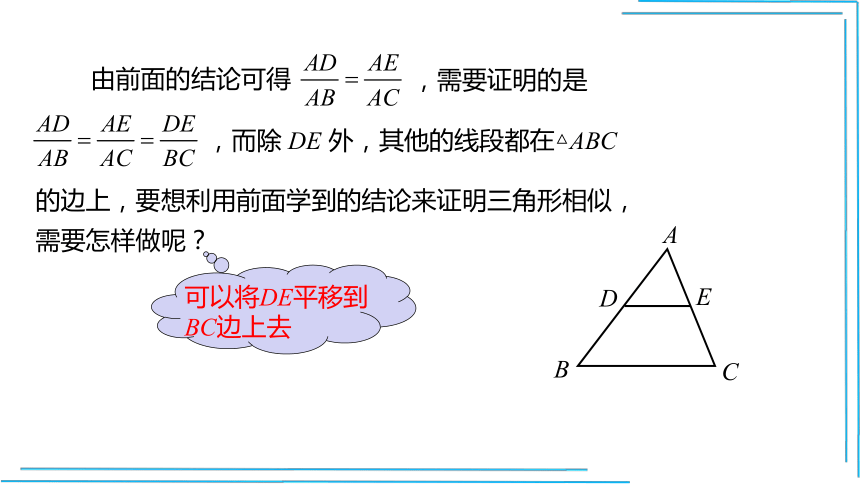
可以将DE平移到BC边上去
,而除 DE 外,其他的线段都在△ABC 的边上,要想利用前面学到的结论来证明三角形相似,
需要怎样做呢?
由前面的结论可得
,需要证明的是
B
C
A
D
E
先证明两个三角形的角分别相等.
如图,在△ADE 与△ABC 中,∠A=∠A.
∵DE//BC,
∴∠ADE=∠B,∠AED=∠C.
再证明两个三角形的边成比例.
过点E作EF//AB,交BC于点F.
∵DE//BC,EF//AB,
A
D
E
B
C
F
∵四边形DBFE是平行四边形,
∴DE=BF.
A
D
E
B
C
F
这样,我们证明了△ADE和△ABC的角分别相等,
边成比例,所以 △ADE∽△ABC.
因此,我们有如下判定三角形相似的定理:
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
对于和两边的延长线相交的情况,结论是否成立?为什么?
问题:如图,DE∥BC,且 DE 分别交 BA,CA 的延长线于点 D,E,△ABC 与△ADE 相似吗?如何证明呢?
D
B
A
l3
l1
l2
C
E
l4
l5
C
D
B
A
E
F
先证明两个三角形的角分别相等.
如图,在△ADE 与△ABC 中,∠DAE=∠BAC.
∵DE//BC,
∴∠D=∠B,∠AED=∠C.
再证明两个三角形的边成比例.
过点E作EF//AB,交CB的延长线于点F.
∵DE//BC,EF//AB,
C
D
B
A
E
F
∵四边形DBFE是平行四边形,
∴DE=BF.
∴ ADE和△ABC的角分别相等,
边成比例,
∴ △ADE∽△ABC.
C
D
B
A
E
F
例题讲解
例1 如图,已知AB∥CD∥EF,AF交BE于点H,
下列结论中错误的是( )
A. B.
C. D.
导引:本题中利用平行线分线段成比例的基本事实的图形主要有“A”型和“X”型,从每种图形中找出比例线段即可判断.
C
解析:根据AB∥CD∥EF,结合平行线分线段成比
例的基本事实可得解.
∵AB∥CD∥EF,
故选项A,B,D正确.
∵CD∥EF,∴ 故选项C错误.
解析: 先根据平行四边形的性质得出AD∥BC,AB∥CD,再根据平行于三角形一边的直线的性质得出对应边成比例即可得出结论.
例2 如图,F是 ABCD的边CD上一点,连接BF,并延长BF交AD的延长线于点E.
求证:
证明:∵四边形ABCD是平行四边形,
∴CD∥AB,AD∥BC.
∴ (平行于三角形一边的直线截其他两边,所得的对应线段成比例).
同理可得
∴
随堂演练
1. 如图,已知AB∥CD∥EF,下列结论正确的是( )
D
2. 如图,在△ABC中,若DE∥BC,EF∥AB,则下
列比例式正确的是( )
A.
B.
C.
D.
C
3. 已知:如图,AB∥EF∥CD,图中共有___对相似三角形.
3
C
D
A
B
E
F
O
4. 如图,在 □ABCD 中,EF∥AB, DE : EA = 2 : 3,
EF = 4,求 CD 的长.
解:∵ EF∥AB,DE : EA = 2 : 3,
D
A
C
B
E
F
∴ △DEF ∽ △DAB,
∴ 即
解得 AB = 10.
又 ∵ 四边形 ABCD 为平行四边形,
∴ CD = AB = 10.
课堂小结
两条直线被一组平行线所截,所得的对应线段成比例
推论
平行于三角形一边的直线截其他两边(或两边延长线),所得的对应线段成比例
相似三角形判定的引理
平行于三角形一边的直线与其他两边相交,所构成的三角形与原三角形相似
基本事实
平行线分线段成比例
https://www.21cnjy.com/help/help_extract.php
第二十七章 相似
27.2.1 第1课时 平行线分线段成比例
随堂演练
课堂小结
获取新知
知识回顾
例题讲解
知识回顾
1、什么叫相似多边形呢?
2、什么叫相似比?
对应角相等,对应边成比例的两个多边形叫做相似多边形
相似多边形的对应边的比叫做相似比
获取新知
对应角相等,对应边成比例的两个三角形叫做相似三角形.
则△ ABC ∽△ A′B′C′.
用符号语言表示:
判定三角形全等,我们并不是验证六个条件,而是利用了几个简便的判定定理(SSS,SAS,ASA,AAS),那么判定三角形相似我们又能不能用类似的简便的判定方法呢?
问题 如图,任意画两条直线a,b ,再画三条与a,b 都相交的平行线l1,l2,l3 .探究l1,l2,l3在直线 a,b 上截得的线段有什么关系.
l3
l1
l2
A
B
C
D
E
F
a
b
通过计算可以得到:
平行线分线段成比例的基本事实:
两条直线被一组平行线所截,所得的对应线段成比例.
说明:
① 定理的条件是“两条直线被一组平行线所截”;
② 是“对应线段成比例”,注意“对应”两字.
l3
l1
l2
A
B
C
D
E
F
a
b
( = ),
左上
左下
右上
右下
( = ).
左下
左上
右下
右上
结论:平行于三角形一边的直线截其他两边(或两边的延长线),
所得的对应线段成比例.
l1
l3
l
l'
A
B
C
D
E
l2
l2
l3
A
B
C
D
E
l1
l
l'
l2
思考:如图,在△ABC 中,DE∥BC,且 DE 分别交 AB,AC 于点 D,E,△ADE 与△ABC 有什么关系?
C
A
B
D
E
我们通过度量三角形的边长,知道△ADE∽△ABC,但要用相似的定义去证明它,我们需要证明什么?
可以将DE平移到BC边上去
,而除 DE 外,其他的线段都在△ABC 的边上,要想利用前面学到的结论来证明三角形相似,
需要怎样做呢?
由前面的结论可得
,需要证明的是
B
C
A
D
E
先证明两个三角形的角分别相等.
如图,在△ADE 与△ABC 中,∠A=∠A.
∵DE//BC,
∴∠ADE=∠B,∠AED=∠C.
再证明两个三角形的边成比例.
过点E作EF//AB,交BC于点F.
∵DE//BC,EF//AB,
A
D
E
B
C
F
∵四边形DBFE是平行四边形,
∴DE=BF.
A
D
E
B
C
F
这样,我们证明了△ADE和△ABC的角分别相等,
边成比例,所以 △ADE∽△ABC.
因此,我们有如下判定三角形相似的定理:
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
对于和两边的延长线相交的情况,结论是否成立?为什么?
问题:如图,DE∥BC,且 DE 分别交 BA,CA 的延长线于点 D,E,△ABC 与△ADE 相似吗?如何证明呢?
D
B
A
l3
l1
l2
C
E
l4
l5
C
D
B
A
E
F
先证明两个三角形的角分别相等.
如图,在△ADE 与△ABC 中,∠DAE=∠BAC.
∵DE//BC,
∴∠D=∠B,∠AED=∠C.
再证明两个三角形的边成比例.
过点E作EF//AB,交CB的延长线于点F.
∵DE//BC,EF//AB,
C
D
B
A
E
F
∵四边形DBFE是平行四边形,
∴DE=BF.
∴ ADE和△ABC的角分别相等,
边成比例,
∴ △ADE∽△ABC.
C
D
B
A
E
F
例题讲解
例1 如图,已知AB∥CD∥EF,AF交BE于点H,
下列结论中错误的是( )
A. B.
C. D.
导引:本题中利用平行线分线段成比例的基本事实的图形主要有“A”型和“X”型,从每种图形中找出比例线段即可判断.
C
解析:根据AB∥CD∥EF,结合平行线分线段成比
例的基本事实可得解.
∵AB∥CD∥EF,
故选项A,B,D正确.
∵CD∥EF,∴ 故选项C错误.
解析: 先根据平行四边形的性质得出AD∥BC,AB∥CD,再根据平行于三角形一边的直线的性质得出对应边成比例即可得出结论.
例2 如图,F是 ABCD的边CD上一点,连接BF,并延长BF交AD的延长线于点E.
求证:
证明:∵四边形ABCD是平行四边形,
∴CD∥AB,AD∥BC.
∴ (平行于三角形一边的直线截其他两边,所得的对应线段成比例).
同理可得
∴
随堂演练
1. 如图,已知AB∥CD∥EF,下列结论正确的是( )
D
2. 如图,在△ABC中,若DE∥BC,EF∥AB,则下
列比例式正确的是( )
A.
B.
C.
D.
C
3. 已知:如图,AB∥EF∥CD,图中共有___对相似三角形.
3
C
D
A
B
E
F
O
4. 如图,在 □ABCD 中,EF∥AB, DE : EA = 2 : 3,
EF = 4,求 CD 的长.
解:∵ EF∥AB,DE : EA = 2 : 3,
D
A
C
B
E
F
∴ △DEF ∽ △DAB,
∴ 即
解得 AB = 10.
又 ∵ 四边形 ABCD 为平行四边形,
∴ CD = AB = 10.
课堂小结
两条直线被一组平行线所截,所得的对应线段成比例
推论
平行于三角形一边的直线截其他两边(或两边延长线),所得的对应线段成比例
相似三角形判定的引理
平行于三角形一边的直线与其他两边相交,所构成的三角形与原三角形相似
基本事实
平行线分线段成比例
https://www.21cnjy.com/help/help_extract.php
