27.2.2 相似三角形的性质 课件(共24张PPT)
文档属性
| 名称 | 27.2.2 相似三角形的性质 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-11 14:08:44 | ||
图片预览







文档简介
(共24张PPT)
第二十七章 相似
27.2.2 相似三角形的性质
随堂演练
课堂小结
获取新知
知识回顾
例题讲解
知识回顾
1. 相似三角形的判定方法有哪几种?
定义:对应边成比例,对应角相等的两个三角形相似
平行于三角形一边,与另外两边相交所构成的
三角形与原三角形相似
三边成比例的两个三角形相似
两边成比例且夹角相等的两个三角形相似
两角分别相等的两个三角形相似
2. 三角形除了三个角,三条边外,还有哪些要素
如果两个三角形相似,
那么,对应的这些要素
有什么关系呢?
高
中线
角平分线
周长
面积
获取新知
如图,△ABC ∽△A′B′C′,相似比为 k,它们对应高、对应中线、对应角平分线的比各是多少?
A
B
C
A'
B'
C'
∵△ABC ∽△A′B′C′,
∴∠B=∠B' ,
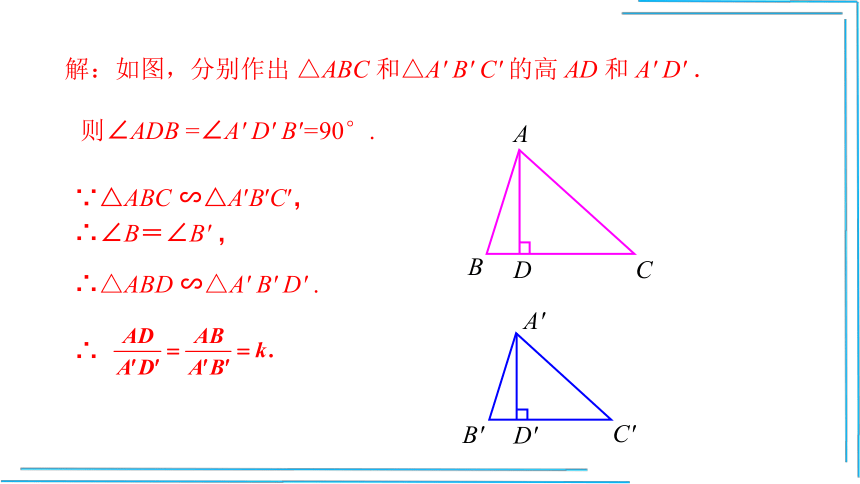
解:如图,分别作出 △ABC 和△A' B' C' 的高 AD 和 A' D' .
则∠ADB =∠A' D' B'=90°.
∴△ABD ∽△A' B' D' .
A
B
C
A'
B'
C'
D'
D
∴
结论: 两个相似三角形对应高的比等于相似比.
试一试:请仿照上述方法猜想并证明两个相似三角形对应中线、对应角平分线的性质.
归纳:
类似地,可以证明相似三角形对应中线、角平分线的比也等于相似比.
一般地,我们有:相似三角形对应线段的比等于相似比.
对应线段包括了对应边,对应边上的中线、高、对应角的平分线
例题讲解
例1 如图,在△ABC中,AD是BC边上的高,矩形EFGH内接于△ABC,且长边FG在BC上,矩形相邻两边的比为1∶2,若BC=30 cm,AD=10 cm,求矩形EFGH的周长.
导引:由四边形EFGH为矩形,得EH∥BC,
所以△AEH与△ABC相似,根据相似三角形对应高的比等于相似比可求出HG的长,进而求出EH的长,即可求得矩形EFGH的周长.
解:设HG=x cm,则EH=2x cm. 易得AP⊥EH.
∵AD=10 cm,∴AP=(10-x) cm.
∵四边形EFGH为矩形,∴EH∥BC,
∴△AEH ∽ △ABC.∴
解得x=6.∴HG=6 cm,EH=12 cm.
∴矩形EFGH的周长为36 cm.
获取新知
全等三角形的周长有何种关系?若相似三角形相似比为k,请你猜想:它们的周长的比与相似比有何关系?请结合图形进行说明,并描述你的结论.
A
B
C
如果 △ABC ∽△A'B'C',相似比为 k,那么
因此
AB=k A'B',BC=kB'C',CA=kC'A',
从而
结论:相似三角形周长的比等于相似比.
例题讲解
例2 已知两个相似三角形的最短边分别为9 cm和6 cm. 若它们的周长之和为60 cm,则这两个三角形的周长分别是多少?
导引:两个相似三角形的最短边就是一组对应边,由此可确定相似比,进而根据已知条件,解以一个三角形周长为未知数的方程即可.
解:设△ABC∽△A1B1C1,且△ABC中的最短边
AC=9 cm,△A1B1C1中的最短边A1C1=6 cm.
则
∴△ABC和△A1B1C1的相似比为
设△ABC的周长为x cm,
则△A1B1C1的周长为(60-x)cm.
∴
∴△ABC的周长为36 cm,△A1B1C1的周长为24 cm.
如果相似三角形的相似比为k,请你猜想:它们的面积的比与相似比有何关系?
由前面的结论,我们有
A
B
C
A'
B'
C'
D'
D
结论:相似三角形面积的比等于相似比的平方.
获取新知
例3 如图,在△ABC 和△DEF 中, AB=2DE ,AC=2DF,∠A=
∠D.若△ABC 的边 BC 上的高为 6,面积为 ,求△DEF 的边 EF 上的高和面积.
B
A
C
D
E
F
解:在△ABC 和△DEF 中,
∵AB=2DE,AC=2DF,
∴
例题讲解
又 ∠D=∠A ,
∴△DEF∽△ABC ,
△DEF 与△ABC 的相似比为 .
∵△ABC 的边BC上的高是 6,面积是 ,
∴△DEF 的边EF上的高为 ×6=3,
面积为
B
A
C
D
E
F
随堂演练
1. 若△ABC∽△DEF,相似比为3∶2,则对应高的比为( )
A.3∶2 B.3∶5
C.9∶4 D.4∶9
A
2. 如图,在Rt△ABC中,∠ACB=90°,∠A= 30°,CD⊥AB于点D,则△BCD与△ABC的周长之比为( )
A.1:2
B.1:3
C.1:4
D.1:5
A
3. 连接三角形两边中点的线段把三角形截成的一个小三角形与原三角形的周长比等于______,面积比等于______.
1 : 2
1 : 4
4. 两个相似三角形对应的中线长分别是 6 cm 和 18 cm,
若较大三角形的周长是 42 cm,面积是 12 cm2,则
较小三角形的周长____cm,面积为____cm2.
14
5. 如图,AB∥CD,AO∶AD=2∶5.
若△AOB的周长为12,求△COD的周长.
课堂小结
1、相似三角形对应边成_______,对应角______.
2、相似三角形对应边上的高、对应边上的中线、
对应角平分线的比都等于________.
3、相似三角形周长的比等于________,
相似三角形面积的比等于______________.
相似比的平方
相似三角形的性质:
比例
相等
相似比
相似比
https://www.21cnjy.com/help/help_extract.php
第二十七章 相似
27.2.2 相似三角形的性质
随堂演练
课堂小结
获取新知
知识回顾
例题讲解
知识回顾
1. 相似三角形的判定方法有哪几种?
定义:对应边成比例,对应角相等的两个三角形相似
平行于三角形一边,与另外两边相交所构成的
三角形与原三角形相似
三边成比例的两个三角形相似
两边成比例且夹角相等的两个三角形相似
两角分别相等的两个三角形相似
2. 三角形除了三个角,三条边外,还有哪些要素
如果两个三角形相似,
那么,对应的这些要素
有什么关系呢?
高
中线
角平分线
周长
面积
获取新知
如图,△ABC ∽△A′B′C′,相似比为 k,它们对应高、对应中线、对应角平分线的比各是多少?
A
B
C
A'
B'
C'
∵△ABC ∽△A′B′C′,
∴∠B=∠B' ,
解:如图,分别作出 △ABC 和△A' B' C' 的高 AD 和 A' D' .
则∠ADB =∠A' D' B'=90°.
∴△ABD ∽△A' B' D' .
A
B
C
A'
B'
C'
D'
D
∴
结论: 两个相似三角形对应高的比等于相似比.
试一试:请仿照上述方法猜想并证明两个相似三角形对应中线、对应角平分线的性质.
归纳:
类似地,可以证明相似三角形对应中线、角平分线的比也等于相似比.
一般地,我们有:相似三角形对应线段的比等于相似比.
对应线段包括了对应边,对应边上的中线、高、对应角的平分线
例题讲解
例1 如图,在△ABC中,AD是BC边上的高,矩形EFGH内接于△ABC,且长边FG在BC上,矩形相邻两边的比为1∶2,若BC=30 cm,AD=10 cm,求矩形EFGH的周长.
导引:由四边形EFGH为矩形,得EH∥BC,
所以△AEH与△ABC相似,根据相似三角形对应高的比等于相似比可求出HG的长,进而求出EH的长,即可求得矩形EFGH的周长.
解:设HG=x cm,则EH=2x cm. 易得AP⊥EH.
∵AD=10 cm,∴AP=(10-x) cm.
∵四边形EFGH为矩形,∴EH∥BC,
∴△AEH ∽ △ABC.∴
解得x=6.∴HG=6 cm,EH=12 cm.
∴矩形EFGH的周长为36 cm.
获取新知
全等三角形的周长有何种关系?若相似三角形相似比为k,请你猜想:它们的周长的比与相似比有何关系?请结合图形进行说明,并描述你的结论.
A
B
C
如果 △ABC ∽△A'B'C',相似比为 k,那么
因此
AB=k A'B',BC=kB'C',CA=kC'A',
从而
结论:相似三角形周长的比等于相似比.
例题讲解
例2 已知两个相似三角形的最短边分别为9 cm和6 cm. 若它们的周长之和为60 cm,则这两个三角形的周长分别是多少?
导引:两个相似三角形的最短边就是一组对应边,由此可确定相似比,进而根据已知条件,解以一个三角形周长为未知数的方程即可.
解:设△ABC∽△A1B1C1,且△ABC中的最短边
AC=9 cm,△A1B1C1中的最短边A1C1=6 cm.
则
∴△ABC和△A1B1C1的相似比为
设△ABC的周长为x cm,
则△A1B1C1的周长为(60-x)cm.
∴
∴△ABC的周长为36 cm,△A1B1C1的周长为24 cm.
如果相似三角形的相似比为k,请你猜想:它们的面积的比与相似比有何关系?
由前面的结论,我们有
A
B
C
A'
B'
C'
D'
D
结论:相似三角形面积的比等于相似比的平方.
获取新知
例3 如图,在△ABC 和△DEF 中, AB=2DE ,AC=2DF,∠A=
∠D.若△ABC 的边 BC 上的高为 6,面积为 ,求△DEF 的边 EF 上的高和面积.
B
A
C
D
E
F
解:在△ABC 和△DEF 中,
∵AB=2DE,AC=2DF,
∴
例题讲解
又 ∠D=∠A ,
∴△DEF∽△ABC ,
△DEF 与△ABC 的相似比为 .
∵△ABC 的边BC上的高是 6,面积是 ,
∴△DEF 的边EF上的高为 ×6=3,
面积为
B
A
C
D
E
F
随堂演练
1. 若△ABC∽△DEF,相似比为3∶2,则对应高的比为( )
A.3∶2 B.3∶5
C.9∶4 D.4∶9
A
2. 如图,在Rt△ABC中,∠ACB=90°,∠A= 30°,CD⊥AB于点D,则△BCD与△ABC的周长之比为( )
A.1:2
B.1:3
C.1:4
D.1:5
A
3. 连接三角形两边中点的线段把三角形截成的一个小三角形与原三角形的周长比等于______,面积比等于______.
1 : 2
1 : 4
4. 两个相似三角形对应的中线长分别是 6 cm 和 18 cm,
若较大三角形的周长是 42 cm,面积是 12 cm2,则
较小三角形的周长____cm,面积为____cm2.
14
5. 如图,AB∥CD,AO∶AD=2∶5.
若△AOB的周长为12,求△COD的周长.
课堂小结
1、相似三角形对应边成_______,对应角______.
2、相似三角形对应边上的高、对应边上的中线、
对应角平分线的比都等于________.
3、相似三角形周长的比等于________,
相似三角形面积的比等于______________.
相似比的平方
相似三角形的性质:
比例
相等
相似比
相似比
https://www.21cnjy.com/help/help_extract.php
