27.3 第2课时 位似图形的坐标变化规律 课件(共20张PPT)
文档属性
| 名称 | 27.3 第2课时 位似图形的坐标变化规律 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-11 14:28:05 | ||
图片预览




文档简介
(共20张PPT)
第二十七章 相似
27.3 第2课时 位似图形的坐标变化规律
随堂演练
课堂小结
获取新知
知识回顾
例题讲解
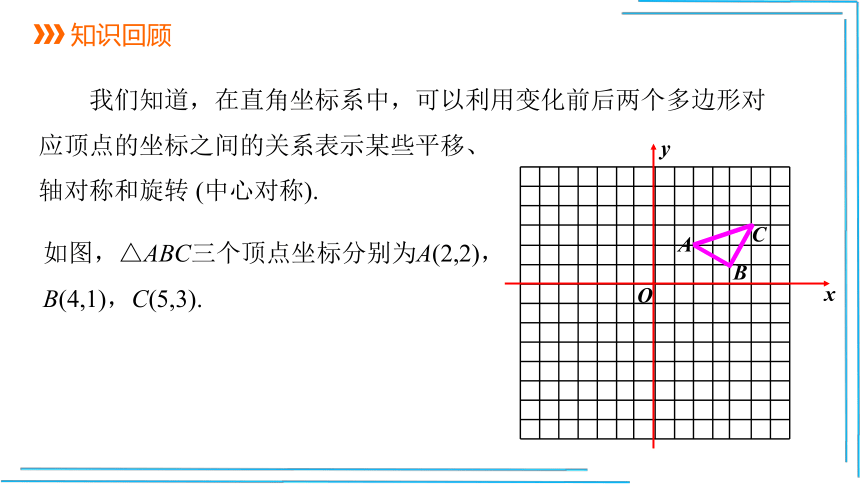
知识回顾
我们知道,在直角坐标系中,可以利用变化前后两个多边形对应顶点的坐标之间的关系表示某些平移、
轴对称和旋转 (中心对称).
如图,△ABC三个顶点坐标分别为A(2,2),
B(4,1),C(5,3).
y
x
A
B
C
O
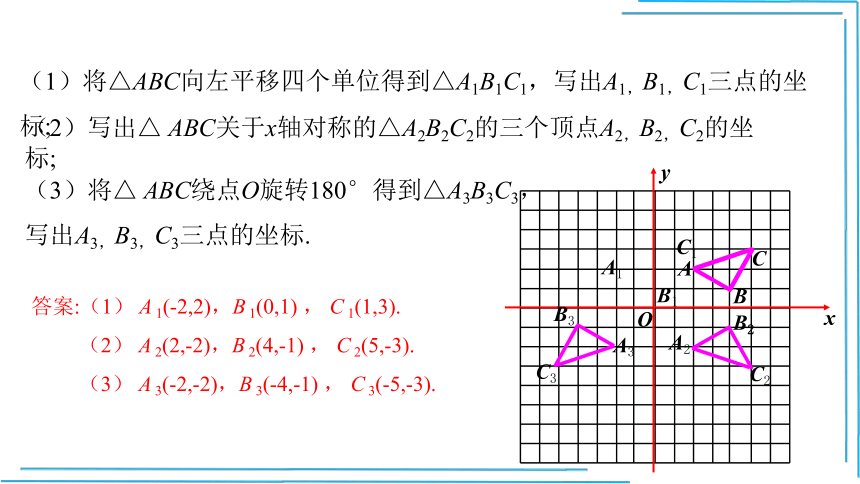
(1)将△ABC向左平移四个单位得到△A1B1C1,写出A1,B1,C1三点的坐标;
(2)写出△ ABC关于x轴对称的△A2B2C2的三个顶点A2,B2,C2的坐标;
(3)将△ ABC绕点O旋转180°得到△A3B3C3,
写出A3,B3,C3三点的坐标.
答案:(1) A 1(-2,2),B 1(0,1) , C 1(1,3).
(2) A 2(2,-2),B 2(4,-1) , C 2(5,-3).
(3) A 3(-2,-2),B 3(-4,-1) , C 3(-5,-3).
y
x
A
B
C
O
A1
B1
C1
A2
A3
B2
B3
C2
C3
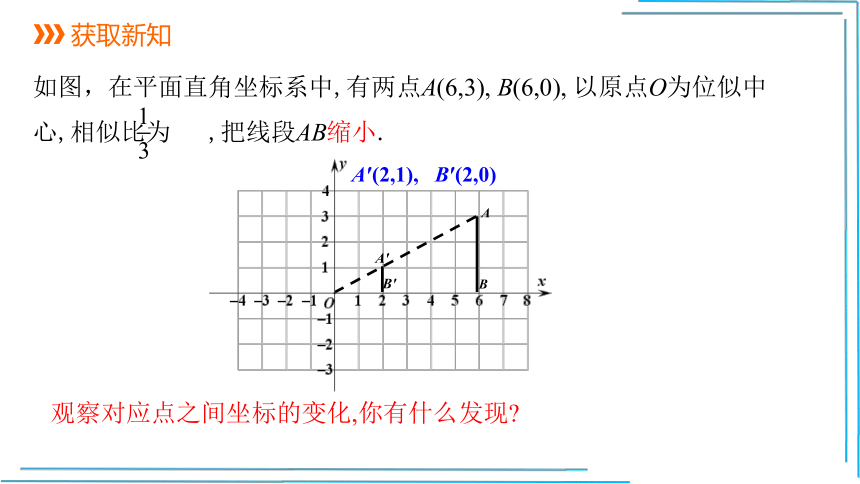
获取新知
如图,在平面直角坐标系中,有两点A(6,3), B(6,0), 以原点O为位似中心,相似比为 ,把线段AB缩小.
A′(2,1), B′(2,0)
B'
A'
B
A
观察对应点之间坐标的变化,你有什么发现
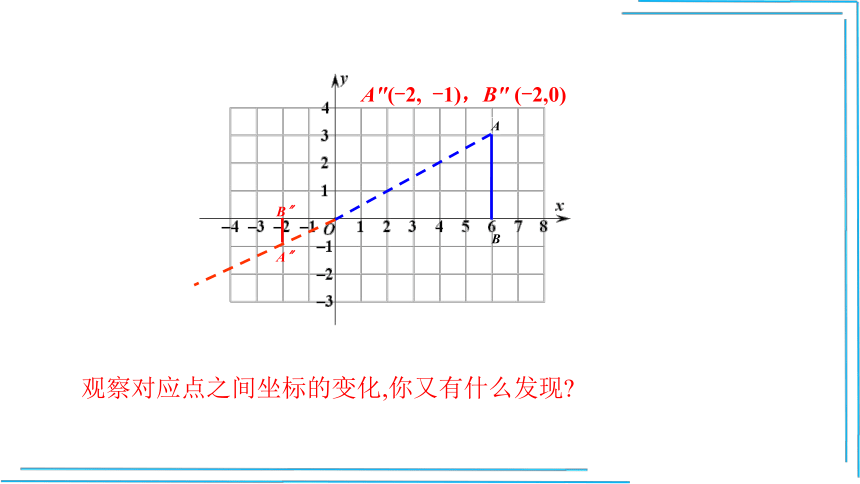
A″(-2, -1),B″ (-2,0)
B
A
A〞
B〞
观察对应点之间坐标的变化,你又有什么发现
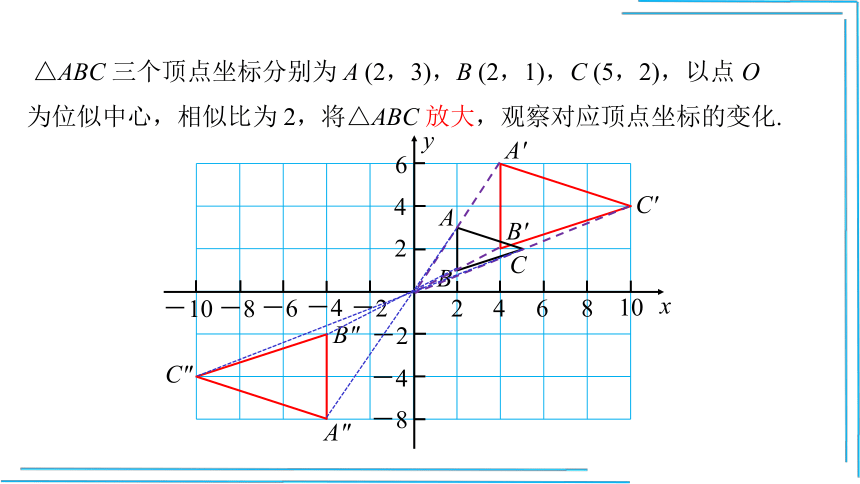
△ABC 三个顶点坐标分别为 A (2,3),B (2,1),C (5,2),以点 O 为位似中心,相似比为 2,将△ABC 放大,观察对应顶点坐标的变化.
2
4
6
4
6
-2
-4
-4
x
y
A
B
2
8
10
C
-2
-6
-8
-10
-8
B'
A'
C'
A"
B"
C"
如图,把 △ABC 放大后 A,B,C 的对应点为
A' ( , ),B' ( , ),C' ( , );
A" ( , ),B" ( , ),C" ( , ).
4
6
4
2
10
4
-4
-6
-4
-2
-10
-4
问题1 在平面直角坐标系中,以原点为位似中心作一个图形的位似图形可以作几个?
问题2 所作位似图形与原图形在原点的同侧,那么对应顶点的坐标的比与其相似比是何关系?如果所作位似图形与原图形在原点的异侧呢?
1. 在平面直角坐标系中,以原点为位似中心作一个
图形的位似图形可以作两个.
归纳:
3. 当 k>1 时,图形扩大为原来的 k 倍;
当 0<k<1时,图形缩小为原来的 .
2. 若位似图形与原图形的位似比为k.
当位似图形在原点同侧时,其对应顶点的坐标为 (kx,ky);
当位似图形在原点两侧时,其对应顶点的坐标为(﹣kx,﹣ky).
例题讲解
例 如图,在平面直角坐标系中,△ABO 三个顶点的坐标分别为 A (-2,4),B (-2,0),O (0,0). 以原点 O 为位似中心,画出一个三角形使它与 △ABO 的相似比为 3 : 2.
2
4
6
2
-2
-4
x
y
A
B
O
提示:画三角形关键是确定它各顶点的坐标. 根据前面的归纳可知,点 A 的对应点 A′ 的坐标为 ,即(-3,6),类似地,可以确定其他顶点的坐标.
解:利用位似中对应点的坐标的变化规律,分别取点
A′ (-3,6),B′ (-3,0),O (0,0).顺次连接点 A′ ,B′ ,O,所得的 △A′ B′ O 就是要画的一个图形.
2
4
6
2
-2
-4
x
y
A
B
O
A′
B′
还有其他画法吗?自己试一试.
随堂演练
1.线段 AB 两个端点的坐标分别为 A (4,4),B (6,2),以原点 O 为位似中心,在第一象限内将线段 AB 缩小为原来的 后得到线段 CD,则端点 D 的坐标为( )
A. (2,2) B. (2,1)
C. (3,2) D. (3,1)
D
x
y
A
B
C
D
2. 如图,线段CD的两个端点的坐标分别为C(1,2),D(2,0),以原点为位似中心,将线段CD放大得到线段AB,若点B的坐标为(5,0),则点A的坐标为( )
A.(2,5) B.(2.5,5)
C.(3,5) D.(3,6)
B
3. 如图,某学习小组在讨论 “变化的鱼”时,知道大鱼与小鱼是位似图形,则小鱼上的点 (a,b) 对应大鱼上的点 .
(-2a,-2b)
4. 在平面直角坐标系中,四边形 OABC 的
顶点坐标分别为 O (0,0),A (6,0),B (3,
6),C (-3,3). 以原点 O 为位似中心,画
出四边形 OABC 的位似图形,使它与四边
形 OABC 的相似比是 2 : 3.
O
C
2
4
6
4
6
-2
-4
x
y
A
B
解:画法一:将四边形 OABC 各顶点的坐标都乘 ;在平面直角坐标系中描点O (0,0),A' (4,0),B' (2,4),C′ (-2,2),用线段顺次连接O,A',B',C'.
O
C
2
4
6
4
6
B'
-2
-4
-4
x
A
B
A'
C'
画法二:将四边形 OABC 各
顶点的坐标都乘 ;在平面直角坐标系中描点O (0,0),
A″ (-4,0),B″ (-2,-4),
C″ (2,-2),用线段顺次连接
O,A″,B″,C″.
O
C
2
4
6
4
6
B″
-2
-4
x
y
A
B
A″
C″
平面直角坐标系中的位似
平面直角坐标系中的位似变换
平面直角坐标系中的图形变换
坐标变化规律
平面直角坐标系中的位似图形的画法
课堂小结
https://www.21cnjy.com/help/help_extract.php
第二十七章 相似
27.3 第2课时 位似图形的坐标变化规律
随堂演练
课堂小结
获取新知
知识回顾
例题讲解
知识回顾
我们知道,在直角坐标系中,可以利用变化前后两个多边形对应顶点的坐标之间的关系表示某些平移、
轴对称和旋转 (中心对称).
如图,△ABC三个顶点坐标分别为A(2,2),
B(4,1),C(5,3).
y
x
A
B
C
O
(1)将△ABC向左平移四个单位得到△A1B1C1,写出A1,B1,C1三点的坐标;
(2)写出△ ABC关于x轴对称的△A2B2C2的三个顶点A2,B2,C2的坐标;
(3)将△ ABC绕点O旋转180°得到△A3B3C3,
写出A3,B3,C3三点的坐标.
答案:(1) A 1(-2,2),B 1(0,1) , C 1(1,3).
(2) A 2(2,-2),B 2(4,-1) , C 2(5,-3).
(3) A 3(-2,-2),B 3(-4,-1) , C 3(-5,-3).
y
x
A
B
C
O
A1
B1
C1
A2
A3
B2
B3
C2
C3
获取新知
如图,在平面直角坐标系中,有两点A(6,3), B(6,0), 以原点O为位似中心,相似比为 ,把线段AB缩小.
A′(2,1), B′(2,0)
B'
A'
B
A
观察对应点之间坐标的变化,你有什么发现
A″(-2, -1),B″ (-2,0)
B
A
A〞
B〞
观察对应点之间坐标的变化,你又有什么发现
△ABC 三个顶点坐标分别为 A (2,3),B (2,1),C (5,2),以点 O 为位似中心,相似比为 2,将△ABC 放大,观察对应顶点坐标的变化.
2
4
6
4
6
-2
-4
-4
x
y
A
B
2
8
10
C
-2
-6
-8
-10
-8
B'
A'
C'
A"
B"
C"
如图,把 △ABC 放大后 A,B,C 的对应点为
A' ( , ),B' ( , ),C' ( , );
A" ( , ),B" ( , ),C" ( , ).
4
6
4
2
10
4
-4
-6
-4
-2
-10
-4
问题1 在平面直角坐标系中,以原点为位似中心作一个图形的位似图形可以作几个?
问题2 所作位似图形与原图形在原点的同侧,那么对应顶点的坐标的比与其相似比是何关系?如果所作位似图形与原图形在原点的异侧呢?
1. 在平面直角坐标系中,以原点为位似中心作一个
图形的位似图形可以作两个.
归纳:
3. 当 k>1 时,图形扩大为原来的 k 倍;
当 0<k<1时,图形缩小为原来的 .
2. 若位似图形与原图形的位似比为k.
当位似图形在原点同侧时,其对应顶点的坐标为 (kx,ky);
当位似图形在原点两侧时,其对应顶点的坐标为(﹣kx,﹣ky).
例题讲解
例 如图,在平面直角坐标系中,△ABO 三个顶点的坐标分别为 A (-2,4),B (-2,0),O (0,0). 以原点 O 为位似中心,画出一个三角形使它与 △ABO 的相似比为 3 : 2.
2
4
6
2
-2
-4
x
y
A
B
O
提示:画三角形关键是确定它各顶点的坐标. 根据前面的归纳可知,点 A 的对应点 A′ 的坐标为 ,即(-3,6),类似地,可以确定其他顶点的坐标.
解:利用位似中对应点的坐标的变化规律,分别取点
A′ (-3,6),B′ (-3,0),O (0,0).顺次连接点 A′ ,B′ ,O,所得的 △A′ B′ O 就是要画的一个图形.
2
4
6
2
-2
-4
x
y
A
B
O
A′
B′
还有其他画法吗?自己试一试.
随堂演练
1.线段 AB 两个端点的坐标分别为 A (4,4),B (6,2),以原点 O 为位似中心,在第一象限内将线段 AB 缩小为原来的 后得到线段 CD,则端点 D 的坐标为( )
A. (2,2) B. (2,1)
C. (3,2) D. (3,1)
D
x
y
A
B
C
D
2. 如图,线段CD的两个端点的坐标分别为C(1,2),D(2,0),以原点为位似中心,将线段CD放大得到线段AB,若点B的坐标为(5,0),则点A的坐标为( )
A.(2,5) B.(2.5,5)
C.(3,5) D.(3,6)
B
3. 如图,某学习小组在讨论 “变化的鱼”时,知道大鱼与小鱼是位似图形,则小鱼上的点 (a,b) 对应大鱼上的点 .
(-2a,-2b)
4. 在平面直角坐标系中,四边形 OABC 的
顶点坐标分别为 O (0,0),A (6,0),B (3,
6),C (-3,3). 以原点 O 为位似中心,画
出四边形 OABC 的位似图形,使它与四边
形 OABC 的相似比是 2 : 3.
O
C
2
4
6
4
6
-2
-4
x
y
A
B
解:画法一:将四边形 OABC 各顶点的坐标都乘 ;在平面直角坐标系中描点O (0,0),A' (4,0),B' (2,4),C′ (-2,2),用线段顺次连接O,A',B',C'.
O
C
2
4
6
4
6
B'
-2
-4
-4
x
A
B
A'
C'
画法二:将四边形 OABC 各
顶点的坐标都乘 ;在平面直角坐标系中描点O (0,0),
A″ (-4,0),B″ (-2,-4),
C″ (2,-2),用线段顺次连接
O,A″,B″,C″.
O
C
2
4
6
4
6
B″
-2
-4
x
y
A
B
A″
C″
平面直角坐标系中的位似
平面直角坐标系中的位似变换
平面直角坐标系中的图形变换
坐标变化规律
平面直角坐标系中的位似图形的画法
课堂小结
https://www.21cnjy.com/help/help_extract.php
