4.2空间图形的公理 公理4,等角定理 课件(共13张PPT)
文档属性
| 名称 | 4.2空间图形的公理 公理4,等角定理 课件(共13张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 496.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-09 00:00:00 | ||
图片预览




文档简介
(共13张PPT)
空 间 平 行 直 线
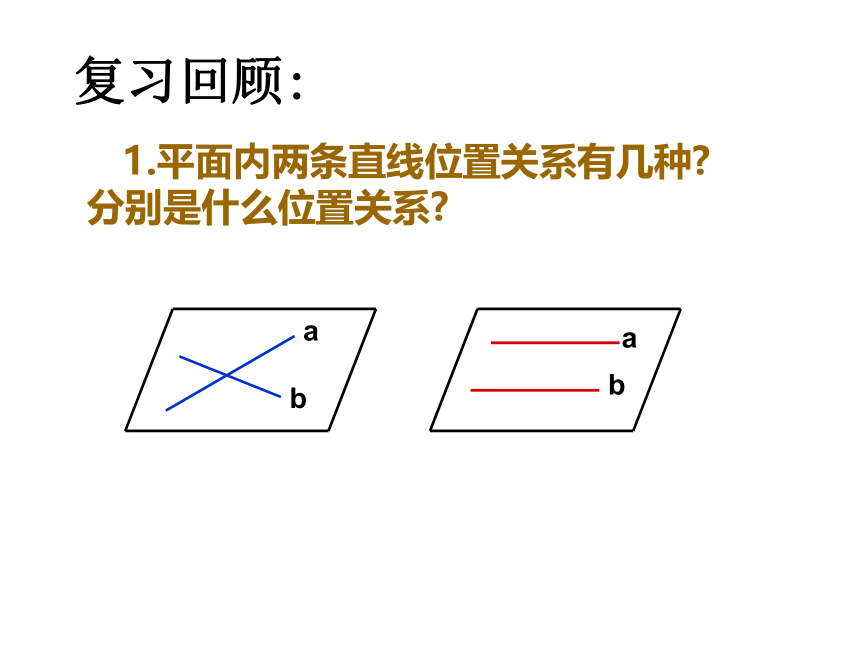
复习回顾:
1.平面内两条直线位置关系有几种
分别是什么位置关系
a
b
a
b
探 讨:
A
B
C
D
A1
B1
C1
D1
观察右图的长方体
ABCD-A1B1C1D1
请同学们看一下图中的直AA1和直线C1D1平行吗?相交吗?
有平行的直线吗?哪些是?
有相交直线吗?哪些是?
定义:我们把不同在任何一个平面内的两条直线叫做异面直线
请同学们思考一下,空间的两条直线的位置关系有哪些呢?
空间两条直线的位置关系有三种:
位置关系 共面情况 公共点个数
相交直线 在同一平面内 有且只有一个
平行直线 在同一平面内 没 有
异面直线 不在任何一平面内 没 有
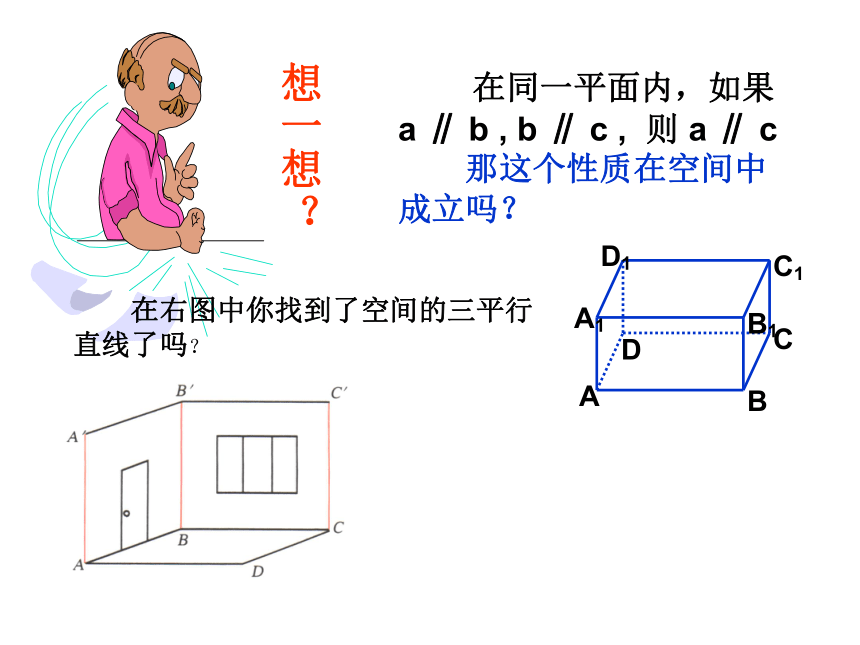
在同一平面内,如果 a ∥ b , b ∥ c , 则 a ∥ c
那这个性质在空间中成立吗?
想一想?
A
B
C
D
A1
B1
C1
D1
在右图中你找到了空间的三平行
直线了吗?
公理4.平行于同一条直线的两条
直线互相平行.
符号表示:
a ∥ b
b ∥ c
a ∥ c
思 考:
经过直线外一点,有几条直线和这条直线平行?
例 题 讲 解 :
例1.如图:在长方体ABCD-A1B1C1D1中,
已知E,F分别是AB , BC 的中点,
求证:EF∥A1C1
A
B
C
D
A1
B1
C1
D1
●
●
E
F
证明:连结AC.
在△ABC中,E,F分别是AB,BC 的中点
所以 EF ∥ AC
又因为 AA1∥BB1 且 AA1 = BB1
BB1∥CC1 且 BB1 = CC1
所以 AA1∥CC1 且 AA1∥CC1
即四边形AA1C1C是平行四边形
所以 AC∥A1C1
从而 EF∥A1C1
想一想?
在平面中,如果一个角的
两边和另一个角的两边分别平
行并且方向相同,那么这两个
角相等,这个结论在空间成立
吗?
观察右图中的∠BEF和
∠B1A1C1 这两个角的两边分别
平行,且有∠BEF = ∠B1A1C1
(因为 ∠BEF = ∠BAC = ∠B1A1C1 )
A
B
C
D
A1
B1
C1
D1
●
●
E
F
定理:如果一个角的两边和另一个角的两边分别
平行并且方向相同,那么这两个角相等.
已知:∠BAC 和 ∠B1A1C1 的边AB ∥ A1B1 ,
AC ∥ A1C1 ,并且方向相同.
求证:∠BAC = ∠B1A1C1
A
A1
C
C1
B
B1
D
D1
E
E1
分析:为证明 ∠BAC=∠B1A1C1, 我们构造两个全等三角形,使∠BAC 与∠B1A1C1是它们的
对应角.
合 作 探 究 :
如果∠BAC 和∠B1A1C1 的边AB∥A1B1 ,
AC∥A1C1 ,且 AB,A1B1 方向相同,而AC
A1C1方向相反, 那么 ∠BAC 和∠B1A1C1
之间有何关系 为什么
结论:空间如果两个角的两条边分别对
应平行,那么这两个角相等或互补.
例 题 讲 解 :
例2.如图,已知E,E1分别是正方体ABCD-A1B1C1D1
的棱AD,A1D1的中点
求证:∠C1E1B1 = ∠CEB
E
E1
A
A1
B
B1
C
C1
D
D1
分析: 设法证明E1C1 ∥ EC
E1B1 ∥ EB
练习巩固:
1.设AA1是正方体的一条棱,这个正方体中
与AA1 平行的棱共有___条.
2.如果OA∥O1A1, OB∥O1B1 ,
那么∠AOB与∠A1O1B1 ( )
A.相等
B.互补
C.相等或互补
D.以上答案都不对
3
C
3.如图,已知 AA1 , BB1 , CC1 ,不共面
且AA1∥BB1, BB1 ∥ CC1 ,AA1 = BB1, BB1 = CC1
求证:△ABC ≌ △A1B1C1
A
A1
B
B1
C
C1
空 间 平 行 直 线
复习回顾:
1.平面内两条直线位置关系有几种
分别是什么位置关系
a
b
a
b
探 讨:
A
B
C
D
A1
B1
C1
D1
观察右图的长方体
ABCD-A1B1C1D1
请同学们看一下图中的直AA1和直线C1D1平行吗?相交吗?
有平行的直线吗?哪些是?
有相交直线吗?哪些是?
定义:我们把不同在任何一个平面内的两条直线叫做异面直线
请同学们思考一下,空间的两条直线的位置关系有哪些呢?
空间两条直线的位置关系有三种:
位置关系 共面情况 公共点个数
相交直线 在同一平面内 有且只有一个
平行直线 在同一平面内 没 有
异面直线 不在任何一平面内 没 有
在同一平面内,如果 a ∥ b , b ∥ c , 则 a ∥ c
那这个性质在空间中成立吗?
想一想?
A
B
C
D
A1
B1
C1
D1
在右图中你找到了空间的三平行
直线了吗?
公理4.平行于同一条直线的两条
直线互相平行.
符号表示:
a ∥ b
b ∥ c
a ∥ c
思 考:
经过直线外一点,有几条直线和这条直线平行?
例 题 讲 解 :
例1.如图:在长方体ABCD-A1B1C1D1中,
已知E,F分别是AB , BC 的中点,
求证:EF∥A1C1
A
B
C
D
A1
B1
C1
D1
●
●
E
F
证明:连结AC.
在△ABC中,E,F分别是AB,BC 的中点
所以 EF ∥ AC
又因为 AA1∥BB1 且 AA1 = BB1
BB1∥CC1 且 BB1 = CC1
所以 AA1∥CC1 且 AA1∥CC1
即四边形AA1C1C是平行四边形
所以 AC∥A1C1
从而 EF∥A1C1
想一想?
在平面中,如果一个角的
两边和另一个角的两边分别平
行并且方向相同,那么这两个
角相等,这个结论在空间成立
吗?
观察右图中的∠BEF和
∠B1A1C1 这两个角的两边分别
平行,且有∠BEF = ∠B1A1C1
(因为 ∠BEF = ∠BAC = ∠B1A1C1 )
A
B
C
D
A1
B1
C1
D1
●
●
E
F
定理:如果一个角的两边和另一个角的两边分别
平行并且方向相同,那么这两个角相等.
已知:∠BAC 和 ∠B1A1C1 的边AB ∥ A1B1 ,
AC ∥ A1C1 ,并且方向相同.
求证:∠BAC = ∠B1A1C1
A
A1
C
C1
B
B1
D
D1
E
E1
分析:为证明 ∠BAC=∠B1A1C1, 我们构造两个全等三角形,使∠BAC 与∠B1A1C1是它们的
对应角.
合 作 探 究 :
如果∠BAC 和∠B1A1C1 的边AB∥A1B1 ,
AC∥A1C1 ,且 AB,A1B1 方向相同,而AC
A1C1方向相反, 那么 ∠BAC 和∠B1A1C1
之间有何关系 为什么
结论:空间如果两个角的两条边分别对
应平行,那么这两个角相等或互补.
例 题 讲 解 :
例2.如图,已知E,E1分别是正方体ABCD-A1B1C1D1
的棱AD,A1D1的中点
求证:∠C1E1B1 = ∠CEB
E
E1
A
A1
B
B1
C
C1
D
D1
分析: 设法证明E1C1 ∥ EC
E1B1 ∥ EB
练习巩固:
1.设AA1是正方体的一条棱,这个正方体中
与AA1 平行的棱共有___条.
2.如果OA∥O1A1, OB∥O1B1 ,
那么∠AOB与∠A1O1B1 ( )
A.相等
B.互补
C.相等或互补
D.以上答案都不对
3
C
3.如图,已知 AA1 , BB1 , CC1 ,不共面
且AA1∥BB1, BB1 ∥ CC1 ,AA1 = BB1, BB1 = CC1
求证:△ABC ≌ △A1B1C1
A
A1
B
B1
C
C1
