2021-2022学年度北师大版高中数学必修2 空间两点间的距离公式 课件(共12张PPT)
文档属性
| 名称 | 2021-2022学年度北师大版高中数学必修2 空间两点间的距离公式 课件(共12张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 692.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-09 00:00:00 | ||
图片预览






文档简介
(共12张PPT)
x
y
P1(x1,y1)
P2(x2, y2)
Q(x2,y1)
O
课前热身
恭喜你
答对了
公式推导
例题讲解
练 习
小 结
作 业
类比
猜想
公式猜想
空间两点:P1(x1,y1,z1), P2(x2,y2,z2)
平面两点:P1(x1,y1), P2(x2,y2)
?
公式推导
?
M2
x
y
z
o
M1
N1
N2
N
M
P2
H
设P1(x1,y1,z1), P2(x2,y2,z2)
则M(x1,y1,0) N(x2,y2,0) H(x2,y2,z1)
P1
同名坐标差的平方和的算术根
例题讲解
例1、给定空间直角坐标系,在x轴上找一点P,使它与点M(4,1,2)的距离为
解:设点P的坐标是(x,0,0),由题意,
|PM|= ,即
所以:(x-4)2=25
解得:x=9 或 x=-1
所以点P的坐标为(9,0,0)或(-1,0,0)
解
原结论成立.
例2、求证以M1(4,3,1), M2(7,1,2), M3(5,2,3),
三点为顶点的三角形是一个等腰三角形
例题讲解
例3、在xoy平面内的直线x+y=1上确定一点M,使M到N(6,5,1)的距离最小
例题讲解
解:由已知,设M(x,1-x,0),则
分析:可设M(x,1-x,0),利用距离公式构造出一个
二次函数后求最值
随堂练习
1、求点M(1,2,-2)到N(-1,0,-1)间的距离
2、 ABC的三个顶点坐标为A(1,-2,-3),B(-1,-1,-1), C(0,0,-5),试判断三角形的形状。
课堂小结
1、空间两点间的距离公式的推导与理解.
2、空间两点间的距离公式的应用.
3、建立适当的空间直角坐标系,综合利用两点间的距离公式.
作业
P93 A组 5、6
谢谢指导!
P2
x
y
z
o
P1
B
C
空间任意两点P1(x1,y1,z1),P2(x2,y2,z2)
作长方体,使P1、P2为其对角线的顶点
由已知得:C(x2,y1,z1),B(x2,y2 ,z1)
即为:空间两点间的距离公式
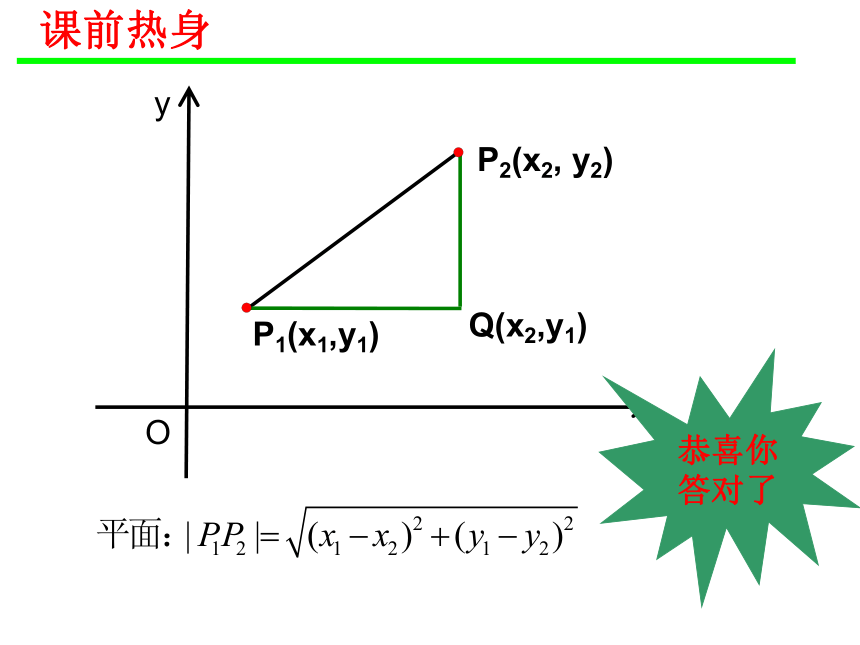
x
y
P1(x1,y1)
P2(x2, y2)
Q(x2,y1)
O
课前热身
恭喜你
答对了
公式推导
例题讲解
练 习
小 结
作 业
类比
猜想
公式猜想
空间两点:P1(x1,y1,z1), P2(x2,y2,z2)
平面两点:P1(x1,y1), P2(x2,y2)
?
公式推导
?
M2
x
y
z
o
M1
N1
N2
N
M
P2
H
设P1(x1,y1,z1), P2(x2,y2,z2)
则M(x1,y1,0) N(x2,y2,0) H(x2,y2,z1)
P1
同名坐标差的平方和的算术根
例题讲解
例1、给定空间直角坐标系,在x轴上找一点P,使它与点M(4,1,2)的距离为
解:设点P的坐标是(x,0,0),由题意,
|PM|= ,即
所以:(x-4)2=25
解得:x=9 或 x=-1
所以点P的坐标为(9,0,0)或(-1,0,0)
解
原结论成立.
例2、求证以M1(4,3,1), M2(7,1,2), M3(5,2,3),
三点为顶点的三角形是一个等腰三角形
例题讲解
例3、在xoy平面内的直线x+y=1上确定一点M,使M到N(6,5,1)的距离最小
例题讲解
解:由已知,设M(x,1-x,0),则
分析:可设M(x,1-x,0),利用距离公式构造出一个
二次函数后求最值
随堂练习
1、求点M(1,2,-2)到N(-1,0,-1)间的距离
2、 ABC的三个顶点坐标为A(1,-2,-3),B(-1,-1,-1), C(0,0,-5),试判断三角形的形状。
课堂小结
1、空间两点间的距离公式的推导与理解.
2、空间两点间的距离公式的应用.
3、建立适当的空间直角坐标系,综合利用两点间的距离公式.
作业
P93 A组 5、6
谢谢指导!
P2
x
y
z
o
P1
B
C
空间任意两点P1(x1,y1,z1),P2(x2,y2,z2)
作长方体,使P1、P2为其对角线的顶点
由已知得:C(x2,y1,z1),B(x2,y2 ,z1)
即为:空间两点间的距离公式
