2021-2022学年度北师大版高中数学必修2 平行关系 课件(共14张PPT)
文档属性
| 名称 | 2021-2022学年度北师大版高中数学必修2 平行关系 课件(共14张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 395.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 07:42:49 | ||
图片预览






文档简介
(共14张PPT)
课前热身
a
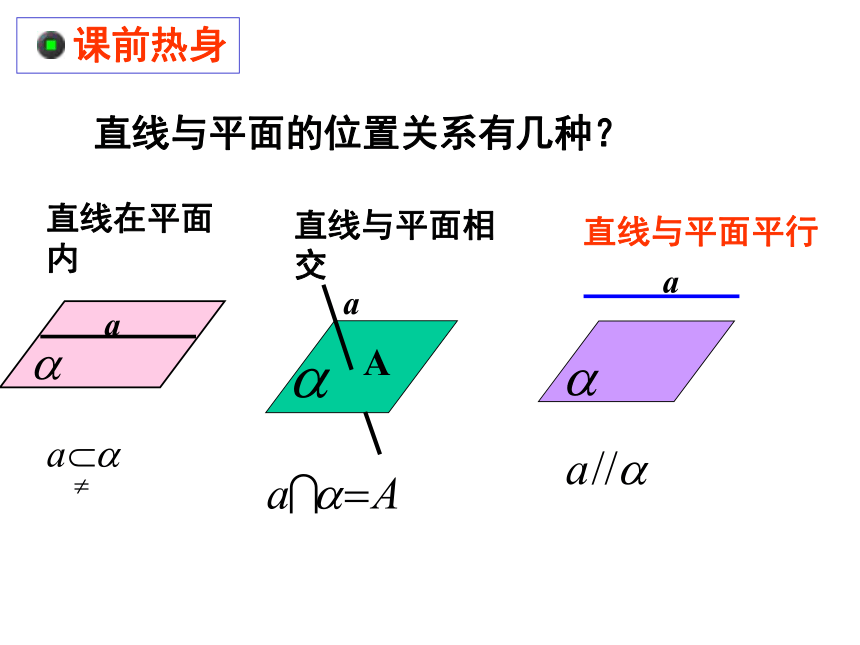
直线在平面内
a
直线与平面平行
直线与平面的位置关系有几种?
a
A
直线与平面相交
问题探究
问题1:请在长方体中找出与直线 平行的平面
问题2:如何判定直线 与平面ABCD平行?
归纳总结
判定直线与平面平行的方法
方法1:利用直线与平面平行的定义
方法2:平面外一条直线与平面内一条直线
平行,则该直线与平面平行.
方法3:两个平面平行,一平面内的任意
一条直线与另一平面平行.
抽象概括
定理5.1 若平面外一条直线与此平面内一条直线平行,则该直线与此平面平行.
图形表示:
符号表示:
线线平行
线面平行
(1)直线 平行于平面 内的一条直线,则 .
//
(4)直线 , ,则 平行于平面 内的无数条直线.
//
(2)若直线 在平面 外,则 .
//
深化认识
下列说法正确的有( )
(3)平面 外 的一条直线 平行于平面 内的一条直线,则 .
//
(3)、(4)
实践应用
例1:空间四边形ABCD中,E、F分别是AB、
AD的中点.判断EF与平面BCD的位置关系.
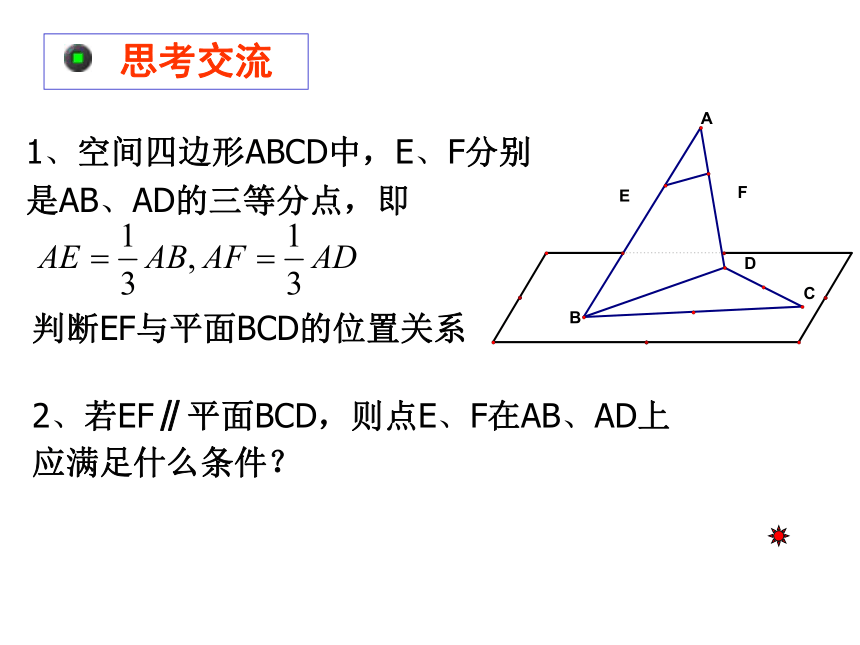
1、空间四边形ABCD中,E、F分别是AB、AD的三等分点,即
思考交流
判断EF与平面BCD的位置关系
2、若EF∥平面BCD,则点E、F在AB、AD上应满足什么条件?
例2、空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、AD的中点.请指出图中满足线面平行位置关系的所有情况。
实践应用
收获与体会
1.判定直线与平面平行的方法:
利用判定定理.
2.转化的思想
空间问题
平面问题
线线平行
线面平行
思考作业
1、课本P34 A组第4题;B组第1题
如图,一个长方体 木料 ,要经过平面 内一点P与棱BC将木料锯开,应该怎样画
直线?
2、
如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.
已知: , ,
求证: .
证明: .
直线与平面平行的性质定理:
例3.一个长方体如图所示.要经过平面A1C1内
一点P和棱BC将木块锯开,应该怎样画线?
例题讲解:
A
B
C
D
A1
B1
C1
D1
.
P
E
F
下课了!
三角形三条中线的交点称为三角形的重心,如图.
若O是三角形的重心则有:
拓展提高
空间四边形ABCD中,E、F分别是面ABD、面BDC
的重心.证明EF∥平面ADC.
课前热身
a
直线在平面内
a
直线与平面平行
直线与平面的位置关系有几种?
a
A
直线与平面相交
问题探究
问题1:请在长方体中找出与直线 平行的平面
问题2:如何判定直线 与平面ABCD平行?
归纳总结
判定直线与平面平行的方法
方法1:利用直线与平面平行的定义
方法2:平面外一条直线与平面内一条直线
平行,则该直线与平面平行.
方法3:两个平面平行,一平面内的任意
一条直线与另一平面平行.
抽象概括
定理5.1 若平面外一条直线与此平面内一条直线平行,则该直线与此平面平行.
图形表示:
符号表示:
线线平行
线面平行
(1)直线 平行于平面 内的一条直线,则 .
//
(4)直线 , ,则 平行于平面 内的无数条直线.
//
(2)若直线 在平面 外,则 .
//
深化认识
下列说法正确的有( )
(3)平面 外 的一条直线 平行于平面 内的一条直线,则 .
//
(3)、(4)
实践应用
例1:空间四边形ABCD中,E、F分别是AB、
AD的中点.判断EF与平面BCD的位置关系.
1、空间四边形ABCD中,E、F分别是AB、AD的三等分点,即
思考交流
判断EF与平面BCD的位置关系
2、若EF∥平面BCD,则点E、F在AB、AD上应满足什么条件?
例2、空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、AD的中点.请指出图中满足线面平行位置关系的所有情况。
实践应用
收获与体会
1.判定直线与平面平行的方法:
利用判定定理.
2.转化的思想
空间问题
平面问题
线线平行
线面平行
思考作业
1、课本P34 A组第4题;B组第1题
如图,一个长方体 木料 ,要经过平面 内一点P与棱BC将木料锯开,应该怎样画
直线?
2、
如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.
已知: , ,
求证: .
证明: .
直线与平面平行的性质定理:
例3.一个长方体如图所示.要经过平面A1C1内
一点P和棱BC将木块锯开,应该怎样画线?
例题讲解:
A
B
C
D
A1
B1
C1
D1
.
P
E
F
下课了!
三角形三条中线的交点称为三角形的重心,如图.
若O是三角形的重心则有:
拓展提高
空间四边形ABCD中,E、F分别是面ABD、面BDC
的重心.证明EF∥平面ADC.
