2021-2022学年度北师大版高中数学必修3课件 北师大版高中数学(必修3)1.7《相关性》(共13张ppt)
文档属性
| 名称 | 2021-2022学年度北师大版高中数学必修3课件 北师大版高中数学(必修3)1.7《相关性》(共13张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 281.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-09 00:00:00 | ||
图片预览





文档简介
(共13张PPT)
相关性
问题1:正方形的面积y与正方形的边长x之间
的函数关系是
y = x2
确定性关系
问题2:某水田水稻产量y与施肥量x之间是否
有一个确定性的关系?
例如:在 7 块并排、形状大小相同的试验田上
进行施肥量对水稻产量影响的试验,得
到如下所示的一组数据:
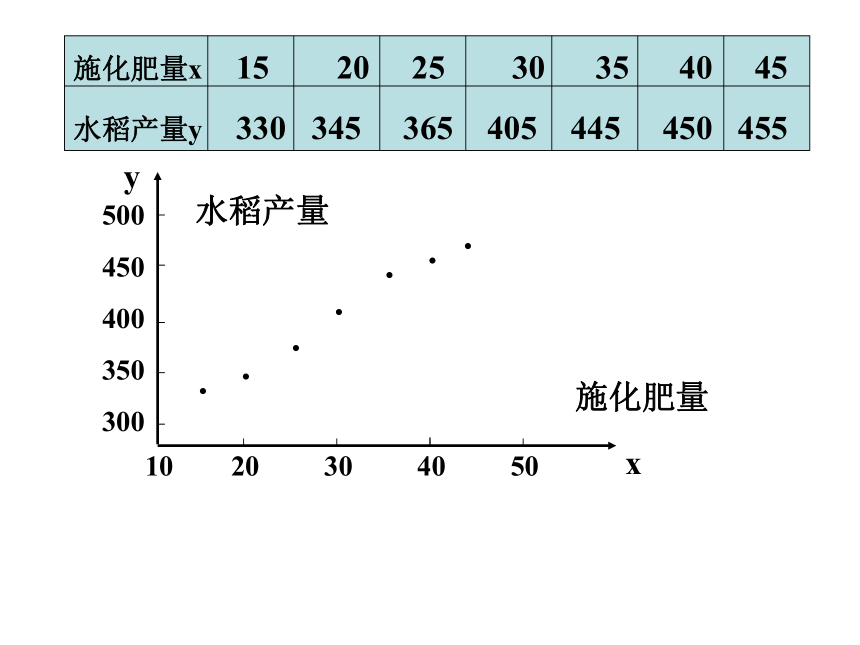
施化肥量x 15 20 25 30 35 40 45
水稻产量y 330 345 365 405 445 450 455
一、变量之间的两种关系
10 20 30 40 50
500
450
400
350
300
·
·
·
·
·
·
·
施化肥量x 15 20 25 30 35 40 45
水稻产量y 330 345 365 405 445 450 455
x
y
施化肥量
水稻产量
自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系。
1、定义:
1):相关关系是一种不确定性关系;
注
对具有相关关系的两个变量进行统计分析的方法叫回归分析。
2):
2、现实生活中存在着大量的相关关系。
如:人的身高与年龄;
产品的成本与生产数量;
商品的销售额与广告费;
家庭的支出与收入。等等
探索:水稻产量y与施肥量x之间大致有何规律?
10 20 30 40 50
500
450
400
350
300
·
·
·
·
·
·
·
发现:图中各点,大致分布在某条直线附近。
探索2:在这些点附近可画直线不止一条,哪条直线最能代表x与y之间的关系呢?
施化肥量x 15 20 25 30 35 40 45
水稻产量y 330 345 365 405 445 450 455
x
y
散点图
施化肥量
水稻产量
1、所求直线方程叫做回归直线方程;
相应的直线叫做回归直线。
2、对两个变量进行的线性分析叫做线性回归分析。
例1:在7块并排、形状大小相同的试验田上进行 施肥对水稻产量影响的试验,得到如下所示的一组数据:
施化肥量x 15 20 25 30 35 40 45
水稻产量y 330 345 365 405 445 450 455
1)、求水稻产量y与施肥量x之间的回归直线方程;
2)、估计当施肥量为70时水稻的产量是多少?
2、回归直线方程:
i 1 2 3 4 5 6 7
xi 15 20 25 30 35 40 45
yi 330 345 365 405 445 450 455
xiyi 4950 6900 9125 12150 15575 18000 20475
x=30 y=399.3
∑xi2=7000 ∑ yi2=1132725 ∑ xiyi=87175
i=1
i=1
7
7
i=1
7
b=(∑ xiyi – n x y)/(∑xi2 - n x 2)
i=1
7
7
i=1
=(87175-7×30×399.3)/(7000-7×302)≈4.75
a= y - b x=399.3 - 4.75 × 30 ≈257
所求的回归直线方程为:y=4.75x+257
二、相关系数
如图是一组观测值的散点图,能否用线性回归方程来表示其分布规律?
问题:
探索:
所求得的回归直线方程,在何种情况下才能对相应的一组观测值具有代表意义呢?
O
y
x
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
称:
为样本相关系数(简称相关系数)
用来衡量y与x之间的线性相关程度。
计算课本P38页表中累积人次与播放天数之间的线性相关系数。
练习:
结论:
|r|≤1,且若 |r| 越接近于1,相关程度越大
若 |r|越接近于0, 相关程度越小。
问题:
r
当|r| 与1接近到何种程度,才表明y与x之间具有线性相关关系呢?
检验步骤:
应用:
点评:
在尚未确定两个变量之间是否存在线性相关关系的情况下,应先进行相关性检验,如确认是线性相关关系后,再求线性回归方程。
1、在附表3中查出与显著性水平0.05与自由度n-2(n为观测值组数)相应的相关系数临界值r 0.05.
2、根据公式计算r 的值。
3、检验所得结果:
如果|r|≤ r 0.05, 则可认为y与x之间的线性相关关系不显著。
如果|r| > r 0.05 ,可认为y与x之间具有线性相关关系。
计算课本P36例中累积人次与播放天数之间是否存在线性相关关系?
结论:
研究线性回归方程,并进而对两个变量的关系进行估计,实际上是将非确定性问题转化为确定性问题进行研究。
练习: P51
小结:
相关性检验及步骤。
作业:P52 习题1.7 T3
相关性
问题1:正方形的面积y与正方形的边长x之间
的函数关系是
y = x2
确定性关系
问题2:某水田水稻产量y与施肥量x之间是否
有一个确定性的关系?
例如:在 7 块并排、形状大小相同的试验田上
进行施肥量对水稻产量影响的试验,得
到如下所示的一组数据:
施化肥量x 15 20 25 30 35 40 45
水稻产量y 330 345 365 405 445 450 455
一、变量之间的两种关系
10 20 30 40 50
500
450
400
350
300
·
·
·
·
·
·
·
施化肥量x 15 20 25 30 35 40 45
水稻产量y 330 345 365 405 445 450 455
x
y
施化肥量
水稻产量
自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系。
1、定义:
1):相关关系是一种不确定性关系;
注
对具有相关关系的两个变量进行统计分析的方法叫回归分析。
2):
2、现实生活中存在着大量的相关关系。
如:人的身高与年龄;
产品的成本与生产数量;
商品的销售额与广告费;
家庭的支出与收入。等等
探索:水稻产量y与施肥量x之间大致有何规律?
10 20 30 40 50
500
450
400
350
300
·
·
·
·
·
·
·
发现:图中各点,大致分布在某条直线附近。
探索2:在这些点附近可画直线不止一条,哪条直线最能代表x与y之间的关系呢?
施化肥量x 15 20 25 30 35 40 45
水稻产量y 330 345 365 405 445 450 455
x
y
散点图
施化肥量
水稻产量
1、所求直线方程叫做回归直线方程;
相应的直线叫做回归直线。
2、对两个变量进行的线性分析叫做线性回归分析。
例1:在7块并排、形状大小相同的试验田上进行 施肥对水稻产量影响的试验,得到如下所示的一组数据:
施化肥量x 15 20 25 30 35 40 45
水稻产量y 330 345 365 405 445 450 455
1)、求水稻产量y与施肥量x之间的回归直线方程;
2)、估计当施肥量为70时水稻的产量是多少?
2、回归直线方程:
i 1 2 3 4 5 6 7
xi 15 20 25 30 35 40 45
yi 330 345 365 405 445 450 455
xiyi 4950 6900 9125 12150 15575 18000 20475
x=30 y=399.3
∑xi2=7000 ∑ yi2=1132725 ∑ xiyi=87175
i=1
i=1
7
7
i=1
7
b=(∑ xiyi – n x y)/(∑xi2 - n x 2)
i=1
7
7
i=1
=(87175-7×30×399.3)/(7000-7×302)≈4.75
a= y - b x=399.3 - 4.75 × 30 ≈257
所求的回归直线方程为:y=4.75x+257
二、相关系数
如图是一组观测值的散点图,能否用线性回归方程来表示其分布规律?
问题:
探索:
所求得的回归直线方程,在何种情况下才能对相应的一组观测值具有代表意义呢?
O
y
x
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
称:
为样本相关系数(简称相关系数)
用来衡量y与x之间的线性相关程度。
计算课本P38页表中累积人次与播放天数之间的线性相关系数。
练习:
结论:
|r|≤1,且若 |r| 越接近于1,相关程度越大
若 |r|越接近于0, 相关程度越小。
问题:
r
当|r| 与1接近到何种程度,才表明y与x之间具有线性相关关系呢?
检验步骤:
应用:
点评:
在尚未确定两个变量之间是否存在线性相关关系的情况下,应先进行相关性检验,如确认是线性相关关系后,再求线性回归方程。
1、在附表3中查出与显著性水平0.05与自由度n-2(n为观测值组数)相应的相关系数临界值r 0.05.
2、根据公式计算r 的值。
3、检验所得结果:
如果|r|≤ r 0.05, 则可认为y与x之间的线性相关关系不显著。
如果|r| > r 0.05 ,可认为y与x之间具有线性相关关系。
计算课本P36例中累积人次与播放天数之间是否存在线性相关关系?
结论:
研究线性回归方程,并进而对两个变量的关系进行估计,实际上是将非确定性问题转化为确定性问题进行研究。
练习: P51
小结:
相关性检验及步骤。
作业:P52 习题1.7 T3
