2021-2022学年度北师大版高中数学必修3课件 北师大版高中数学(必修3)1.8《最小二乘估计》(共14张)
文档属性
| 名称 | 2021-2022学年度北师大版高中数学必修3课件 北师大版高中数学(必修3)1.8《最小二乘估计》(共14张) |  | |
| 格式 | ppt | ||
| 文件大小 | 457.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-09 17:24:12 | ||
图片预览






文档简介
(共14张PPT)
最小二乘估计
问题导入:
上一节课我们学习了人的身高与右手一拃长之间近似存在着线性关系,这种线性关系可以有多种方法来进行刻画,那么用什么样的线性关系刻画会更好?这就是本节课我们要讨论的问题。
最小二乘估计
用什么样的线性关系刻画会更好一些?
问题1:
想法:保证这条直线与所有点都近(也就是距离最小)。
最小二乘法就是基于这种想法。
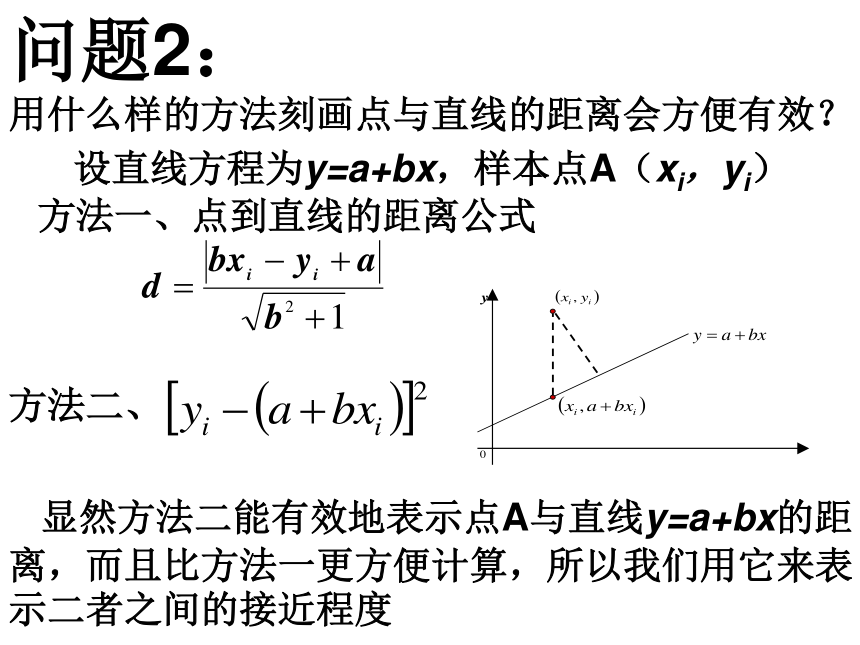
问题2:
用什么样的方法刻画点与直线的距离会方便有效?
设直线方程为y=a+bx,样本点A(xi,yi)
方法一、点到直线的距离公式
方法二、
显然方法二能有效地表示点A与直线y=a+bx的距离,而且比方法一更方便计算,所以我们用它来表示二者之间的接近程度
问题3:
怎样刻画多个点与直线的接近程度?
例如有5个样本点,其坐标分别为(x1,y1),(x2,y2),(x3,y3),(x4,y4),(x5,y5)与直线y=a+bx的接近程度:
若有n个样本点:(x1,y1),… ,(xn,yn),可以用下面的表达式来刻画这些点与直线y=a+bx的接近程度:
使上式达到最小值的直线y=a+bx就是所求的直线,这种方法称为最小二乘法。
抽象概括:
这样得到的直线方程称为线性回归方程,a,b为其系数。
1、在回归直线方程中,b是回归直线方程的斜率,a是截距;b的含义容易理解成增加的单位数,而实际上,它代表x每增加一个单位,y的平均增加单位数。一般的说,当回归系数b>0时,说明两个变量呈正相关关系,它的意义是:当x每增加一个单位时,y就增加b个单位;当b<0时,说明两个变量呈负相关关系,它的意义是:当x每增加一个单位时,y就减少b
个单位。
2、回归直线必经过点
注:
求线性回归方程的系数:
线性回归方程:
x x1 x2 x3 x4 …. xn
y y1 y2 y3 y4 …. yn
3.
例题1 从某大学中随机选出8名女大学生,其身高和体重数据如下表:
编号 1 2 3 4 5 6 7 8
身高 165 165 157 170 175 165 155 170
体重 48 57 50 54 64 61 43 59
求根据一名女大学生的身高预报她的体重的回归方程,并预报一名身高为172cm的女大学生的体重。
1. 散点图;
2.回归方程:
分析:由于问题中要求根据身高预报体重,因此选取身高为自变量,体重为因变量.
例2:上节中的练习热茶的杯数(y)与气温(x)
之间是线性相关的
1)求线性回归方程
2)如果某天的气温是-30C,预测这天
能卖热茶多少杯?
气温 26 18 13 10 4 -1
杯数 20 24 34 38 50 64
课堂练习:
1.设一个回归方程为y=3-1.2x,则变量x增加一个单位时
( )
A.y平均增加1.2个单位 B.y平均增加1.2个单位
C.y平均减少3个单位 D.y平均减少3个单位
2.在一次实验中,测得(x,y)的四组值为(1,2),(2,3),(3,4),(4,5),则y与x之间的回归直线方程为( )
A.y=x+1 B. y=x+2 C. y=2x+1 D. y=x-1
A
A
1.如何求线性回归方程(公式法)
小结:
2.线性回归方程系数的含义
3.线性回归方程的应用
最小二乘估计
问题导入:
上一节课我们学习了人的身高与右手一拃长之间近似存在着线性关系,这种线性关系可以有多种方法来进行刻画,那么用什么样的线性关系刻画会更好?这就是本节课我们要讨论的问题。
最小二乘估计
用什么样的线性关系刻画会更好一些?
问题1:
想法:保证这条直线与所有点都近(也就是距离最小)。
最小二乘法就是基于这种想法。
问题2:
用什么样的方法刻画点与直线的距离会方便有效?
设直线方程为y=a+bx,样本点A(xi,yi)
方法一、点到直线的距离公式
方法二、
显然方法二能有效地表示点A与直线y=a+bx的距离,而且比方法一更方便计算,所以我们用它来表示二者之间的接近程度
问题3:
怎样刻画多个点与直线的接近程度?
例如有5个样本点,其坐标分别为(x1,y1),(x2,y2),(x3,y3),(x4,y4),(x5,y5)与直线y=a+bx的接近程度:
若有n个样本点:(x1,y1),… ,(xn,yn),可以用下面的表达式来刻画这些点与直线y=a+bx的接近程度:
使上式达到最小值的直线y=a+bx就是所求的直线,这种方法称为最小二乘法。
抽象概括:
这样得到的直线方程称为线性回归方程,a,b为其系数。
1、在回归直线方程中,b是回归直线方程的斜率,a是截距;b的含义容易理解成增加的单位数,而实际上,它代表x每增加一个单位,y的平均增加单位数。一般的说,当回归系数b>0时,说明两个变量呈正相关关系,它的意义是:当x每增加一个单位时,y就增加b个单位;当b<0时,说明两个变量呈负相关关系,它的意义是:当x每增加一个单位时,y就减少b
个单位。
2、回归直线必经过点
注:
求线性回归方程的系数:
线性回归方程:
x x1 x2 x3 x4 …. xn
y y1 y2 y3 y4 …. yn
3.
例题1 从某大学中随机选出8名女大学生,其身高和体重数据如下表:
编号 1 2 3 4 5 6 7 8
身高 165 165 157 170 175 165 155 170
体重 48 57 50 54 64 61 43 59
求根据一名女大学生的身高预报她的体重的回归方程,并预报一名身高为172cm的女大学生的体重。
1. 散点图;
2.回归方程:
分析:由于问题中要求根据身高预报体重,因此选取身高为自变量,体重为因变量.
例2:上节中的练习热茶的杯数(y)与气温(x)
之间是线性相关的
1)求线性回归方程
2)如果某天的气温是-30C,预测这天
能卖热茶多少杯?
气温 26 18 13 10 4 -1
杯数 20 24 34 38 50 64
课堂练习:
1.设一个回归方程为y=3-1.2x,则变量x增加一个单位时
( )
A.y平均增加1.2个单位 B.y平均增加1.2个单位
C.y平均减少3个单位 D.y平均减少3个单位
2.在一次实验中,测得(x,y)的四组值为(1,2),(2,3),(3,4),(4,5),则y与x之间的回归直线方程为( )
A.y=x+1 B. y=x+2 C. y=2x+1 D. y=x-1
A
A
1.如何求线性回归方程(公式法)
小结:
2.线性回归方程系数的含义
3.线性回归方程的应用
